基于优化代价函数的三电平ANPC并网逆变器电流预测控制方法
2021-04-15王楠窦智峰李琰琰武洁
王楠,窦智峰,李琰琰,武洁
郑州轻工业大学 电气信息工程学院,河南 郑州 450002
0 引言
近年来,随着能源需求的不断扩大和环境保护意识的日益增强,电力领域内高转换效率和低谐波含量的分布式可再生能源发电需求不断增加.三电平并网逆变器作为电能转换的主要设备之一,广泛应用于风力发电、储能、微型智能电网、电动汽车等领域.三电平有源中点钳位(ANPC)并网逆变器具有较高的转换效率和灵活的运行方式,在太阳能发电、海上风力发电等新型可再生能源的中高压交流传动、柔性输电、电网无功补偿和吸收等方面都有重要应用[1-3].但中点电压不平衡问题一直是三电平并网逆变器的研究热点,具体表现为中点电压直流偏置和中点电压低频纹波增加,进而对电能转换系统的可靠性造成严重危害[4-6].
在不改变系统结构的前提下,有效的控制策略是解决中点电压不平衡问题的主要方式,其中有限控制集模型预测控制(FCS-MPC)方法已经在两电平逆变器领域得到了广泛应用和深入研究,并取得了较好的经济效益和环境效益.相比传统两电平并网逆变器,三电平并网逆变器具有输出负载电流谐波少、控制效果好等优点,是中压大功率逆变器的主要拓扑结构[7-12],如何将FCS-MPC方法应用于三电平并网逆变器成为当前的研究热点.FCS-MPC方法基于三电平并网逆变器有限的27种开关组合矢量状态,通过建立三电平ANPC并网逆变器数学预测模型并采用滚动计算代价函数最优解的方法,选择使系统定义的目标函数最小的开关状态作用于逆变器,达到抑制中点电压波动和减少输出电流谐波的目的,具有控制简单、灵活、无需脉宽调制等优点[4-5].针对三电平电压源并网逆变器的中点电压波动问题,在对三电平ANPC并网逆变器建模过程中,传统的模型预测控制方法需要对每相开关状态进行判断,不能直接采用27种开关状态,其控制流程复杂,计算过程时间长,而且控制效率不高,容易导致逆变器开关损耗的增加和中点电压的波动.文献[13]设计了一种在线修正分支定界的方法,其中优化计算部分包含系统跟踪性和开关损耗优化项的指标函数,通过函数来实施滚动优化以达到控制目的.该方法鲁棒性好,在系统多变量受约束的情况下,减少了高次谐波的含量,但计算量较大、控制方法较复杂,对中点电压波动的控制并不理想.文献[14]通过引入基于递推最小二乘法的电感在线辨识算法,提高了三电平并网逆变器系统的参数鲁棒性,但所辨识的电感参数与电感实际值有差异,计算方法稍显复杂.鉴于此,本文拟提出一种基于优化代价函数的三电平ANPC并网逆变器电流预测控制方法,直接以逆变器开关状态对代价函数进行计算和求值,以期减少输出电流的谐波含量,降低中点电压波动,减小总谐波畸变率.
1 三电平ANPC并网逆变器建模
三电平ANPC并网逆变器简化电路如图1所示.由图1可知,三电平ANPC并网逆变器主体结构为三相,每相包括6个开关管,其中2个开关管的中点都连接到直流侧母线电容的中点上.所以,ANPC的每一相相对于直流侧母线电容中性点产生3个相位(Udc/2,0,-Udc/2).以开关状态变量Sx表示x相的开关状态,这里的x∈{a,b,c},用符号P、O和N分别表示每相产生的3个相位.三电平ANPC并网逆变器三相产生的空间矢量相位如图2所示.
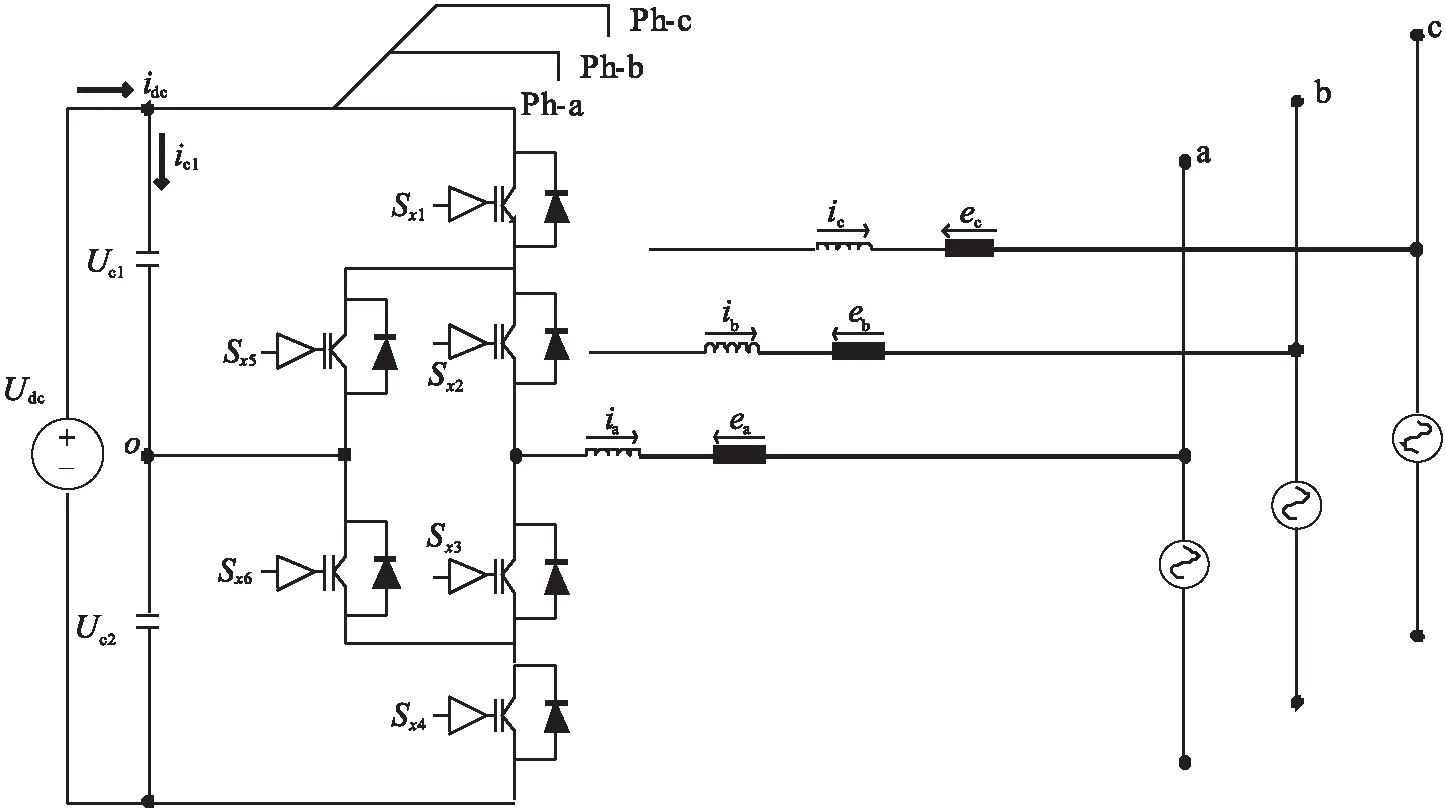
图1 三电平ANPC并网逆变器简化电路Fig.1 Three-level ANPC grid-connected inverter simplified circuit
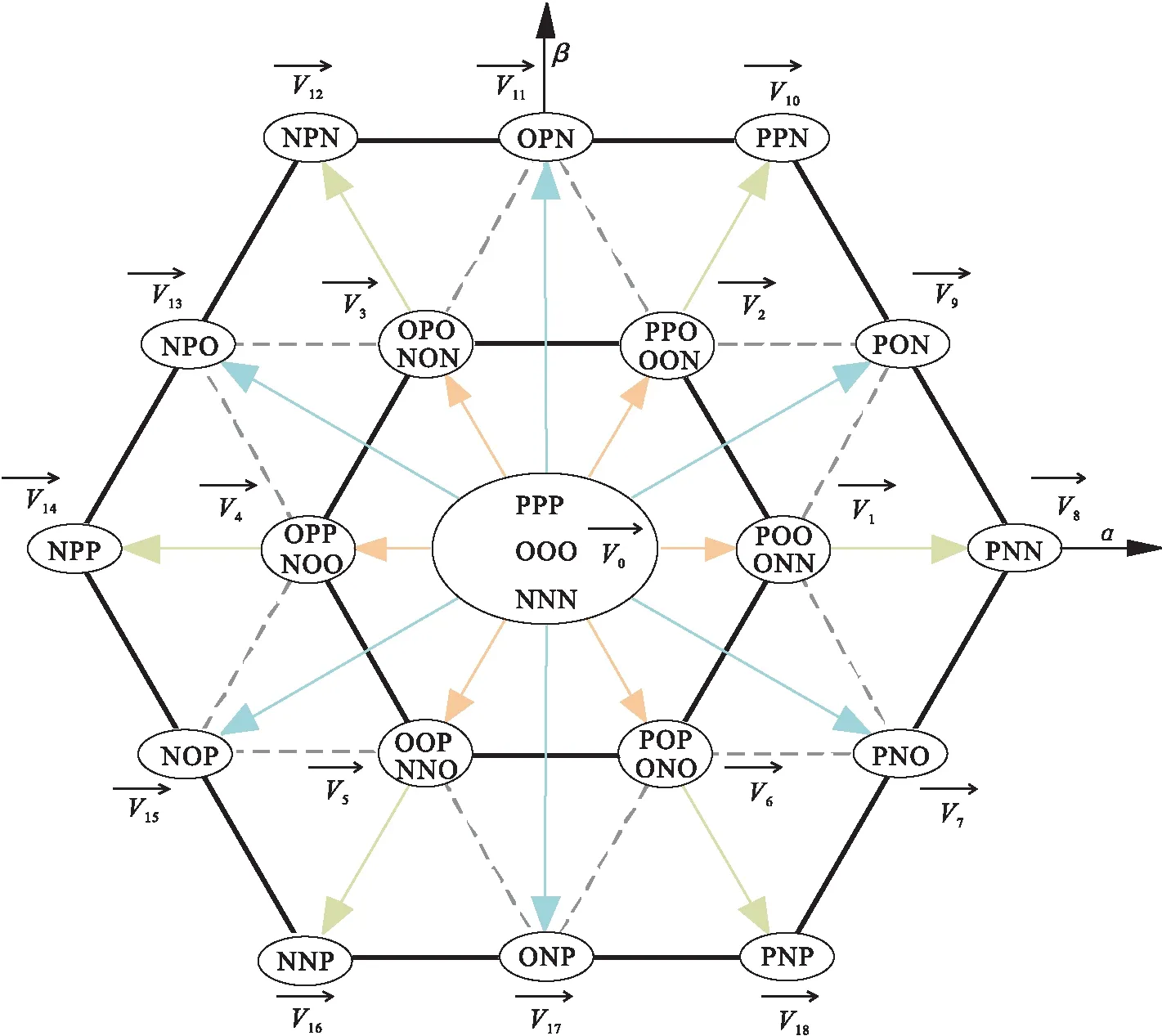
图2 三电平ANPC并网逆变器空间矢量图Fig.2 Three-level ANPC grid-connected inverter space vector
由图2可知,三电平ANPC并网逆变器三相可产生27种开关状态,其对应电压矢量中有8个冗余矢量(包括2个冗余零矢量),表1为逆变器某一相的开关状态.
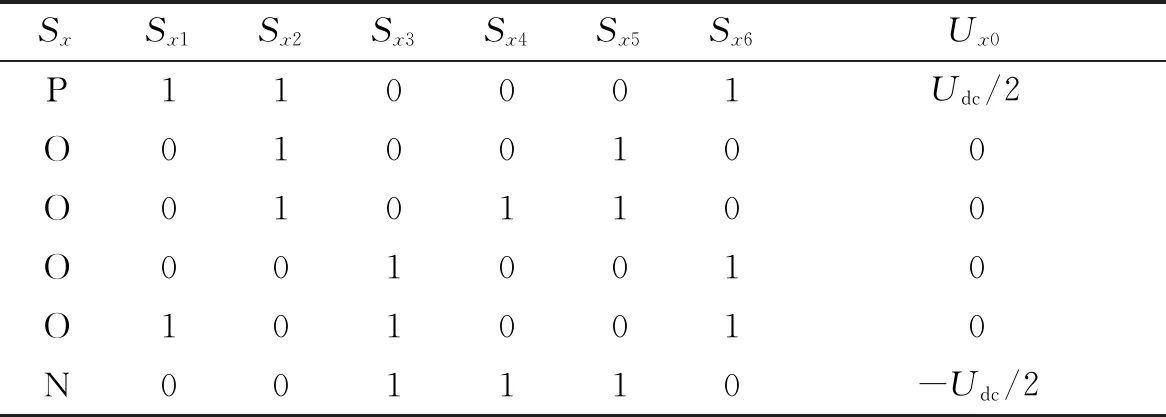
表1 某一相的开关状态
三电平ANPC并网逆变器的a,b,c相每相产生的3个相位对应每个桥臂的3种通断情况:Sx= P表示第x相的Sa1,Sa2,Sa6开关管闭合,其余开关管断开,其输出电压是Udc/2;Sx=O表示第x相输出电压是0时,4种不同的开关管通断情况;Sx=N表示第x相的Sa3,Sa4,Sa5开关管闭合,其余开关管断开,其输出电压是-Udc/2.因此,逆变器的输出电压可以表示为
Uxo=SxUdc
则逆变器输出三相电压可以描述为
逆变器输出电压矢量为
假定三相逆变器系统平衡,电网电压为正弦且对称,则并网电流矢量i和电网电压矢量e可分别定义为
则连续时域内并网电压动态方程为
①
2 传统电流预测控制方法
传统有限控制集模型预测控制的直流侧环节电容器电压的动态过程可以通过以下电容差分方程进行描述:
②
其中,C为电容值.采样时刻Ts的电容电压为导数近似值:
③
故式②、③对应的离散时间方程为
④
其中,电流ic1(k)和ic2(k)依赖逆变器开关状态和输出电流的值,可通过下式进行定义:
其中,idc为电压源Udc所产生的电流;开关状态决定变量H1x和H2x的值,并通过下式进行定义:
输出负载电流矢量的离散时间模型为

⑤
其中,V(k)为所要评价的27个矢量;δ(k)为负载反向电动势,其离散时间模型为
对于由ANPC并网逆变器所产生的27种开关状态,首先测量每个开关状态下电容器的负载电流和电压的当前值,电容器的负载电流和电压的预测值可通过式④⑤得到,再选择使开关状态评估代价函数g最小的开关状态,并在下一个采样时刻使用,其预测控制框图如图3所示.其中代价函数g为
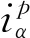
3 基于优化代价函数的电流预测控制方法
传统模型预测控制的基本原理是由逆变器输出电流预测值与参考电流值差的绝对值、直流侧两个电容电压的绝对值得到代价函数,求得该代价函数的极小值,即得系统最优解,并输出最佳的开关状态.但是传统方法中增加了电容电压差和开关状态关系的中间变量,使得三电平并网逆变器系统中点电压振荡较高.因此本文直接利用开关状态与电容电压差的关系,建立数学模型,优化传统方法.通过Clark变换,在αβ坐标系下通过系统数学模型充分利用逆变器的离散化特征进行预测算法设计.变换公式可表示为
[αβ]T=T3/2[abc]
其中T3/2为变换矩阵:
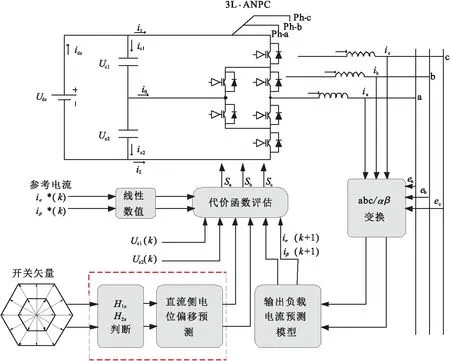
图3 传统有限控制集模型预测控制框图Fig.3 Traditional finite control set model prediction block diagram
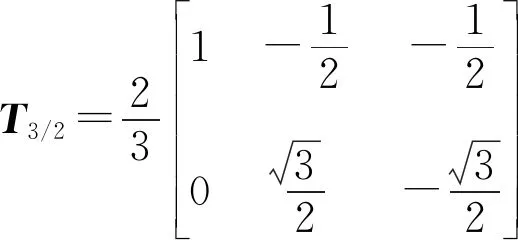
根据基尔霍夫电压定律和式①,可得:
⑥
假定三相电网电压平衡(ea+eb+ec=0),可得三电平并网逆变器在静止αβ坐标系下的模型为
其中,eα和eβ、iα和iβ、Uα和Uβ分别是静止αβ坐标系下三电平并网逆变器网侧电压、电流和交流侧电压.根据三电平整流器的直流母线电压和其开关状态,可得三电平并网逆变器交流侧电压Uα和Uβ为
⑦
在三电平并网逆变器高频数学模型中,直流侧中点电位偏移量与开关函数的关系如下:
在一个采样周期内,对式⑥中的导数进行前向欧拉近似处理,得k+1时刻电流预测值为
将式⑦进行离散化,可得k+1采样时刻直流侧电位偏移的预测值为
⑧
其中,ΔUc(k)=Uc2(k)-Uc1(k).三电平并网逆变器的控制目标是快速跟踪参考电流和平衡中点电位,因此设定代价函数为
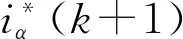
改进的有限控制集模型预测控制框图如图4所示.
4 仿真结果与分析
为了验证本文基于优化代价函数的电流预测控制方法的有效性,对传统电流预测控制方法和本文方法进行建模仿真.仿真参数如表2所示,仿真结果如图5—7所示.

表2 仿真参数
由图5可知,在某一段时刻,由于ANPC并网逆变器系统中以某一种开关矢量状态的持续输出作为最优解,造成这段时间内其中点电压波动较大;本文优化方法建立的模型直流侧中点电压波动显著减小,由改进前的60 V降到了改进后的1 V以内,并且波形整体波动更有规律、更加对称,说明其27种开关状态都得到应用.由图6和图7可知,传统方法的输出负载电流波形总体良好,但电流谐波畸变率较高(1.89%);本文优化方法使得三电平ANPC并网逆变器的输出负载电流谐波畸变率减小至1.14%.
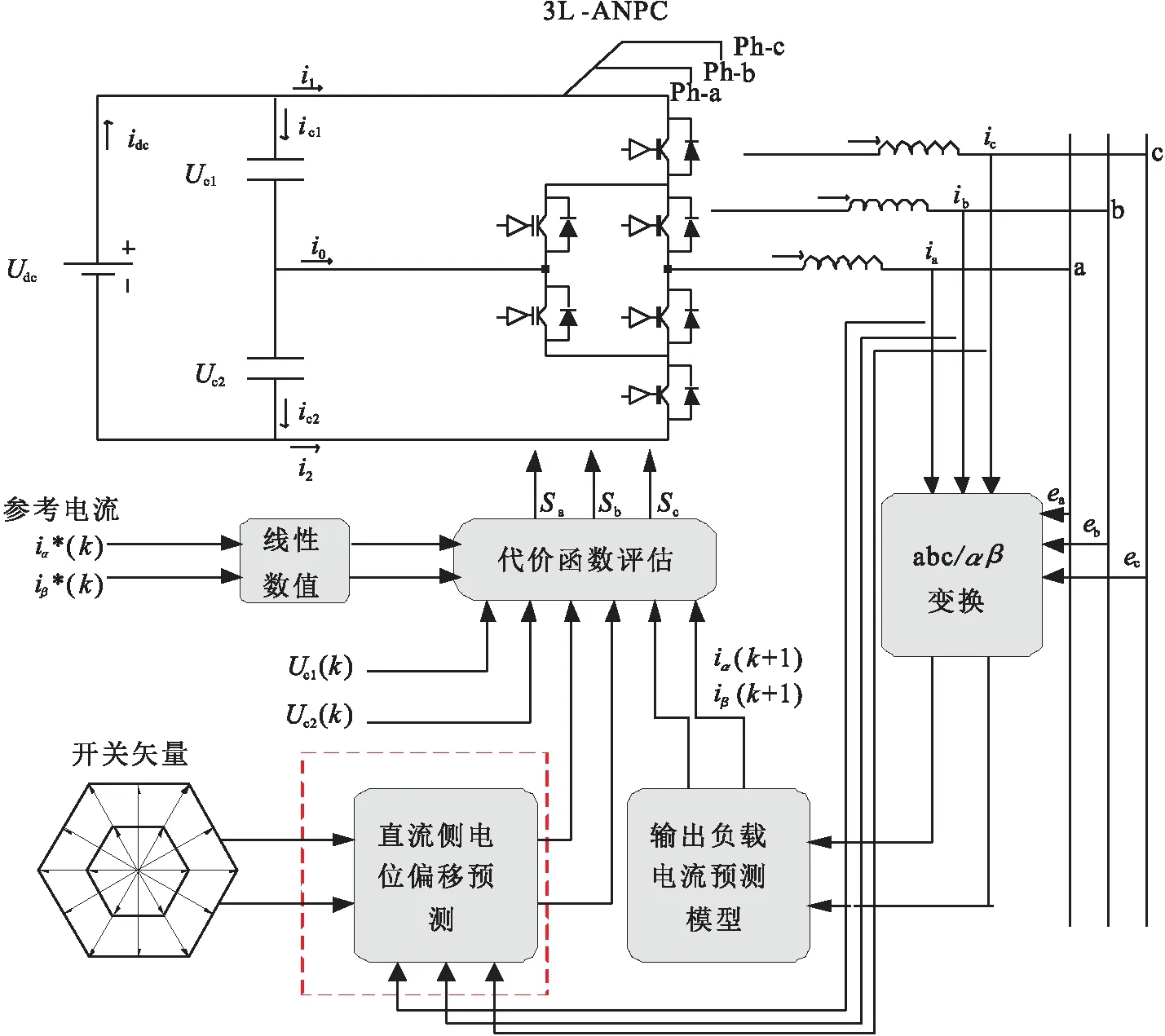
图4 改进的有限控制集模型预测控制框图Fig.4 Improved finite control set model predictive control block diagram
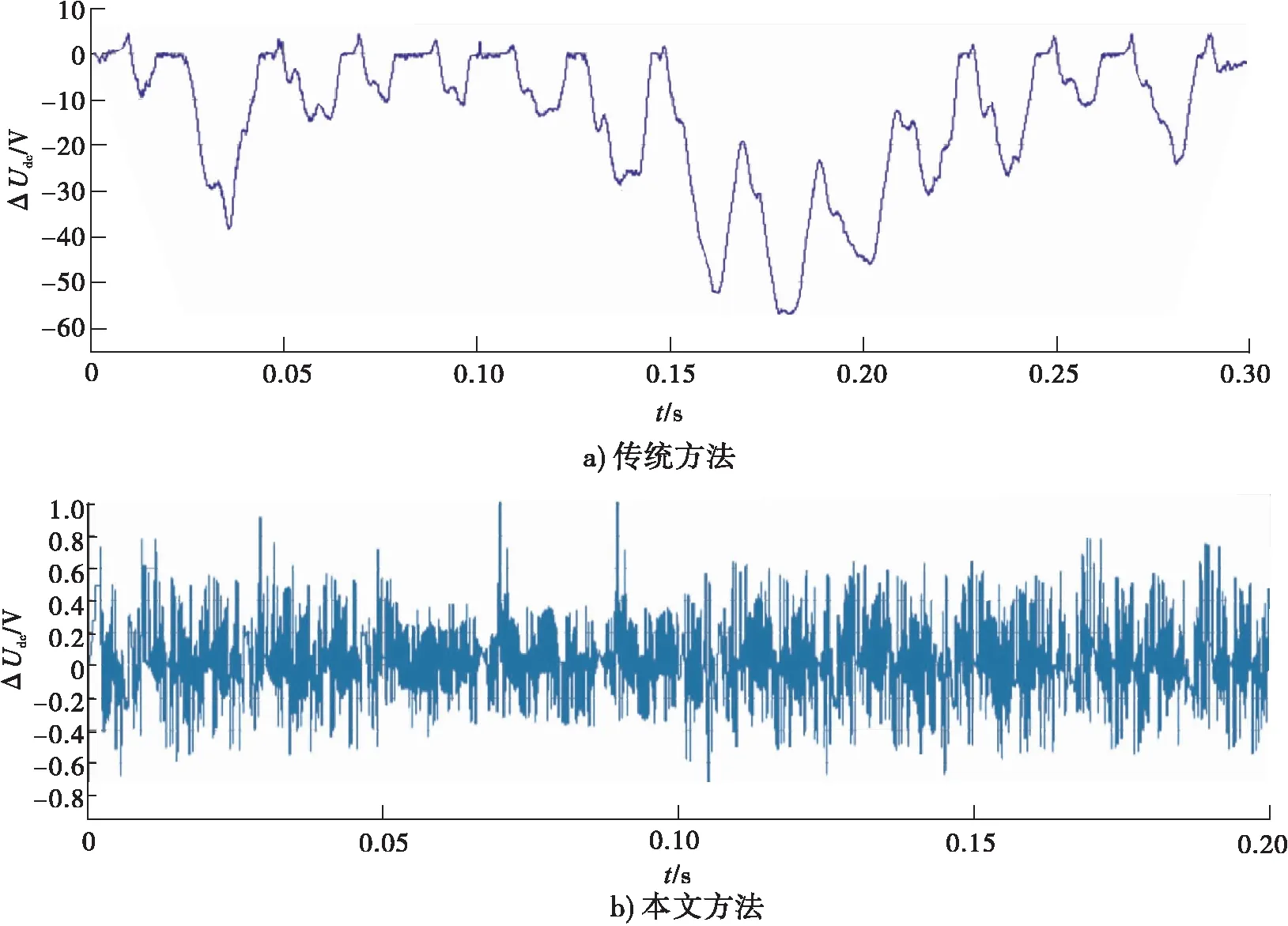
图5 中点电压波形Fig.5 Mid-point voltage waveform
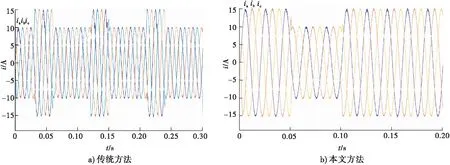
图6 输出负载电流波形Fig.6 Output load current waveform
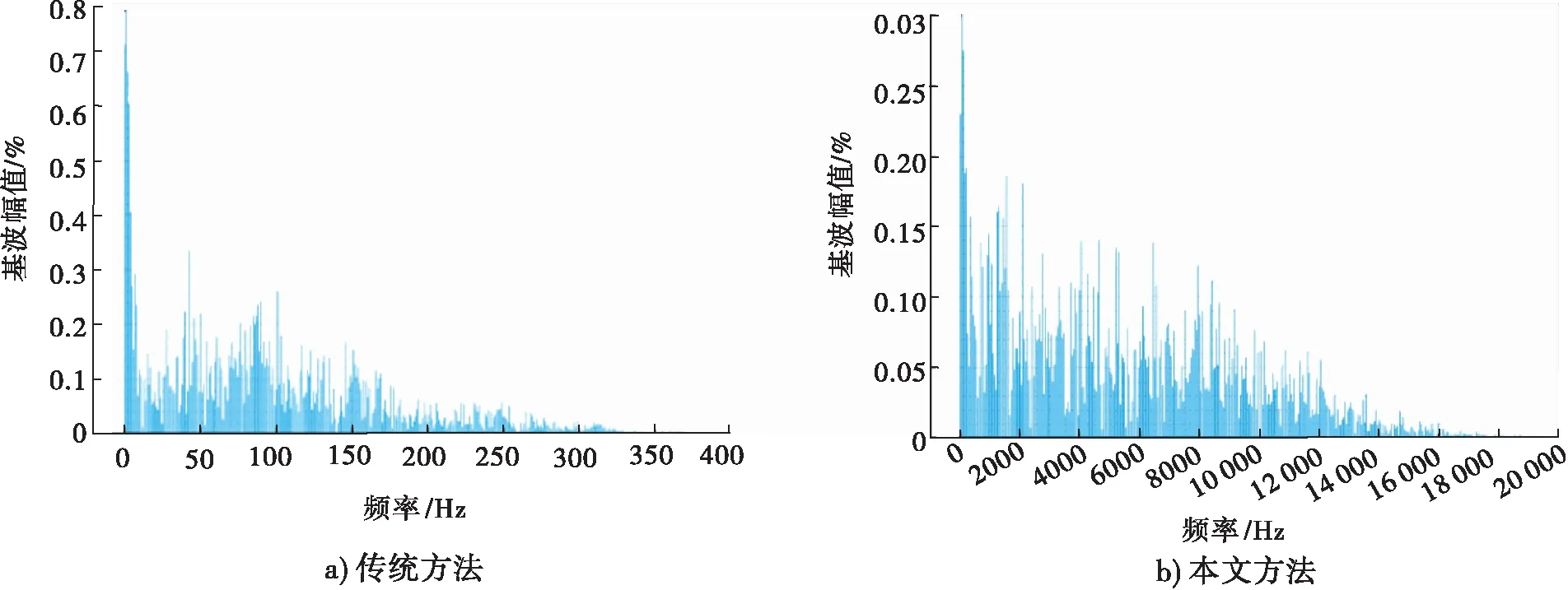
图7 负载电流谐波分析Fig.7 Load current harmonic analysis
5 实验结果与分析
为验证本文方法在实际工程应用中的有效性,设计如下实验平台:直流侧电源采用MywayAPL-II的可编程双向直流电源,交流侧并网部分采用Ametek型号为MX30的可编程交流电源,并采用横河DLM4000系列8通道示波器记录实验结果.实验所用参数与上述仿真参数一致,实验结果如图8—9所示.
由图8可知,优化的模型预测控制方法电流波形效果较好,电流谐波畸变率由3.72%降至3.34%,验证了本文方法的有效性.由图9可知,相比传统有限控制集模型预测电流控制方法,本文方法中点电压波动显著减少,输出电流谐波畸变率得到控制.
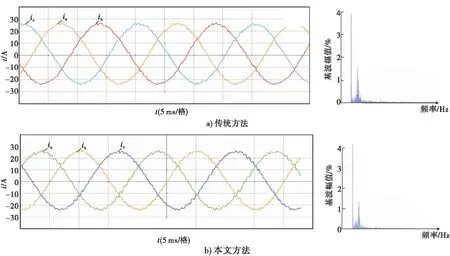
图8 电流预测控制实验波形Fig.8 Current predictive control experimental waveform
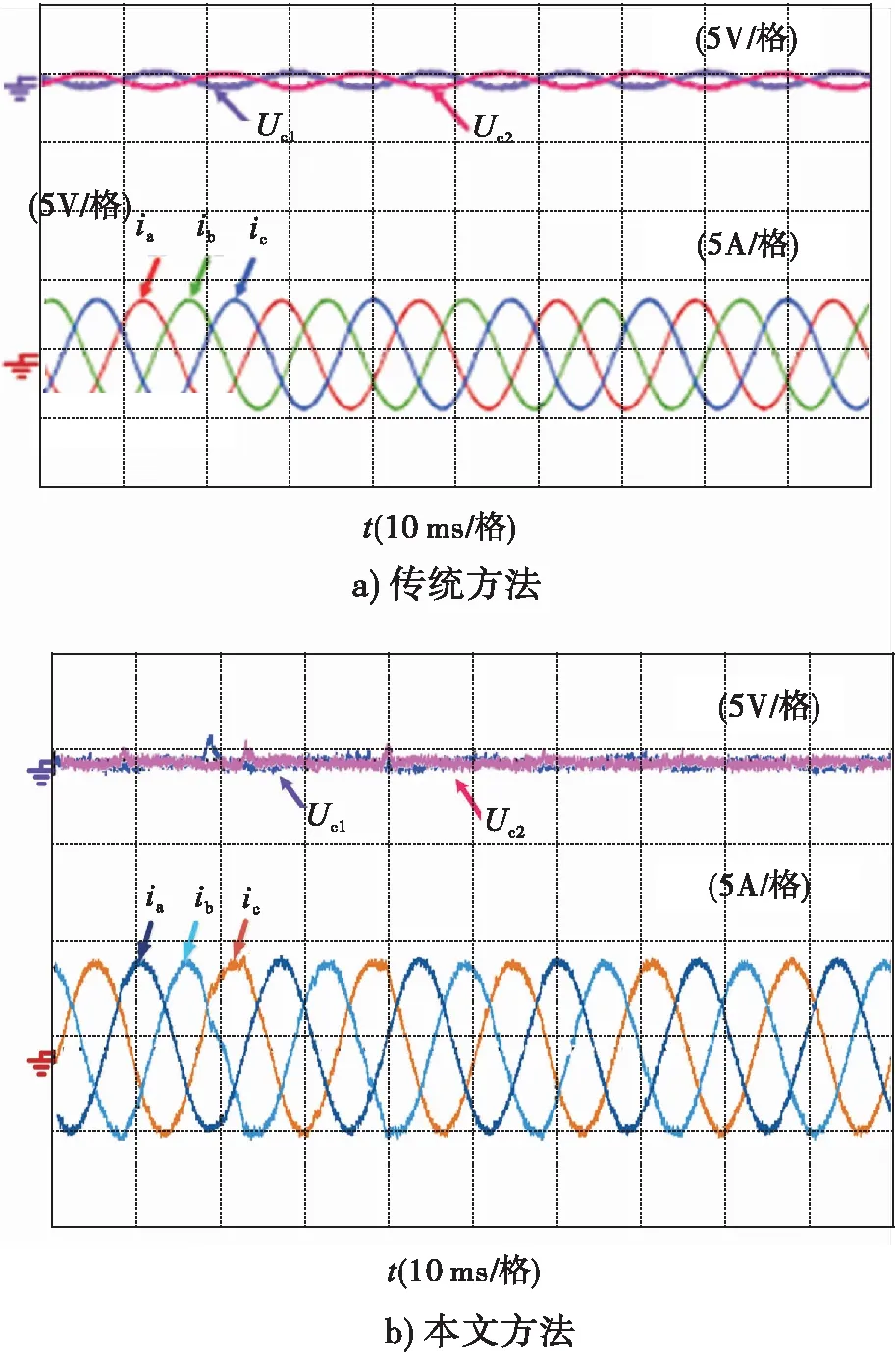
图9 中点电压波动实验波形Fig.9 Mid-point voltage fluctuation experimental waveform
6 结论
本文提出了一种基于优化代价函数的三电平ANPC并网逆变器电流预测控制方法,建立了三电平ANPC三相逆变器在静止αβ坐标系下直流侧母线电容中点电压与逆变器输出电流之间的关系,并对传统有限控制集模型预测控制方法和改进的有限控制集模型预测控制方法进行对比.仿真和实验结果表明,本文方法有较好的控制效果,直流侧母线电容电压波动由60 V 降到了1 V以内;改进的有限控制集模型预测控制有良好的稳态性能和优越的动态性能,仿真结果显示电流谐波畸变率由1.89%降至1.14%,实验结果显示电流谐波畸变率由3.72% 降至3.34%.本文只针对单个目标进行预测控制,为了得到更好的控制效果,今后可以进行多个目标同时预测控制研究.
