机械锥齿轮传动机构的优化设计
2021-04-15谭伟美
谭伟美
(广西玉林农业学校,广西 玉林 537000)
0 引言
在各类齿轮机构中,锥齿轮系统的主要功能为传递2根相交的轴间的运动及动力。与圆柱型齿轮系统一样,锥齿轮系统分为许多种类。根据轮齿的外形,将锥齿轮的结构分为直齿型锥齿轮、斜齿型锥齿轮、螺旋型锥齿轮几类。锥齿轮结构的传动过程的优势主要有传动效率比较高、传动比比较稳定、工作状态可靠、结构比较紧凑、占用空间小、耐磨损能力强、使用寿命长以及噪声比较低。现阶段,锥齿轮系统的传动在许多领域中得到了比较广泛的应用。当前锥齿轮系统传动的结构优化设计的重要目标是在符合系统承载量级的前提下,选取适合的齿轮副系统数据,使传动系统的空间占比最小,保证整体结构的紧凑性。
1 结构优化设计的背景
现阶段,我国相关工程技术人员针对锥齿轮系统的传动过程的实验及分析研究比较深入。某技术人员将减速器装置的外形尺寸及结构强度方面的设计参数归结到约束条件的范畴,创建了相关数学模型,使用MATLAB软件中的结构优化工具单元实施锥齿轮结构的优化设计工作,通过程序解其传动机构的体积数值及最小目标函数的解。其他技术人员用齿轮机构的模数及传动比等相关参数作为相关参数的设计变量,把齿轮的齿面及齿根强度数值和结构之间没有产生干涉现象作为主要的约束条件,将齿轮副结构的传动过程的总中心距取最小值,设置为系统的目标函数,使用MATLAB软件的优化工具单元进行方程的求解。其他技术人员将齿轮系统的相关参数综合为1套结构优化的数学模型,综合粒子群的优化算法进行相关目标函数的解析。上述工程技术人员的研究目标都是为了使齿轮副可以取相对较小的空间体积,不过同样可能出现某些问题,例如不能符合齿轮系统传动过程的多参数的优化需求,齿轮副结构的啮合状态下的重合程度不满足要求、齿轮结构的强度较低,导致齿轮结构传动过程的稳定性降低[1]。
该文设计了1套锥齿轮系统的传动机构的结构优化相关的数学模型,使用遗传式计算方法及MATLAB软件的优化工具模块,针对目标函数进行方程的求解。遗传式的计算方法主要思路是模拟达尔文的进化论相关的自然选择及遗传学有关原理,是1类持续挑选优秀独立体的随机模式检索算法,一直持续到在全体中检索出最佳独立体。遗传式计算方法具有针对繁杂多峰值函数的通用性及针对目标函数的全方位优化特性等优点,在相关工程领域改进设计过程中得到了广泛应用,尤其是在结构参数信息改进设计、神经型网络系统、生产安排调整、模态分析、自动适应巡航控制工程等行业中,遗传式计算方法使多重目标函数解析更简便,在实际应用中获得了比较理想效果。
2 锥齿轮定义
锥齿轮是用于传递2根相互交叉轴间的运动状态及动力载荷,在常规机械装置内,锥齿轮系统两轴间的交叉角度为90°(然而个别情况也可能不是90°)。与圆柱形齿轮相似,锥齿轮系统存在分度圆锥、齿轮顶部圆锥、齿轮根部圆锥及基准圆锥。由于圆锥体存在大端与小端,该齿轮相应大端的圆分别是分度圆(该圆半径是r)、齿顶圆、齿根圆及基准圆。1组锥齿轮的运动轨迹等同于1组节圆锥进行纯滚动运动[2]。锥齿轮如图1所示。

图1 锥齿轮结构
3 锥齿轮传动装置研究
在锥齿轮传动机构中,把旋转轮的中心轮轴a当作输入零件,为了确保锥齿轮传动机构的传动比不变,旋转轮的中心轮轴的内齿b上设置一级加速锥齿轮副进行传动,锥齿轮的系杆机构H作为输出零件,这种方式可以使锥齿轮的扭矩降低。锥齿轮传动机构原理图如图2所示。
4 锥齿轮受力分析
与圆柱形齿轮相似,将理论法线方向的荷载在小齿轮均匀分度圆位置分成直齿锥齿轮受力分量,即为圆周方向的分力、径向方向的分力和轴向方向的分力,各个分力的朝向如图2所示。然后再按照受力平衡法则及各个分力间的空间几何联系进行计算。

图2 锥齿轮传动机构原理图
齿轮传动的类型很多,按照不同的分类方法可以分为不同的类型。
5 锥齿轮传动的技术特点及应用研究
锥齿轮传动的技术特点是减小了小端面的齿顶高度,进而降低了齿顶凸尖的概率;且齿根圆直径比较大,有益于提升锥轮齿的载荷能力、刀具使用周期及润滑储油。锥齿轮的优点是使用寿命长、荷承载力高、耐腐蚀性强、噪声及减震较低、自身重力重量轻、造价低廉、易于加工成型及润滑性能优等。
由于锥齿轮通常应用于轻载及低速的状况。因此,锥齿轮通常应用在大型工业传动机器、汽车差速器、电力机车、大型船只、供电网络、钢铁制造企业及铁路轨道信号检测中。
6 结构优化理论模型
相关工程技术人员在锥齿轮传动机构的优化设计过程中,将锥齿轮副的总体积最小化作为主要设计目的。如图3所示,传动轴交叉角是90°的锥齿轮副,主体外形尺寸参数包括分度圆锥角度数值δ、锥齿轮副锥间距数值R、分度圆直径数值d以及锥齿轮宽度数值b等[3]。
通常来讲,锥齿轮副的总体积V用如下公式表示为:
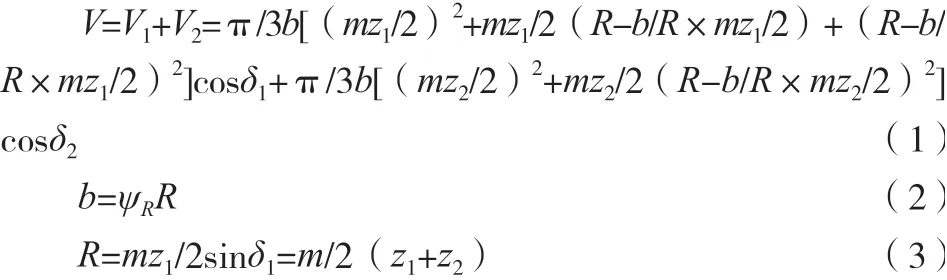
式中:z1、z2分别为大锥齿轮和小锥齿轮的齿数;m为锥齿轮副系统的大端一侧的模数;R为锥齿轮副系统的锥距值;b为锥齿轮部件的宽度数值;ψR为齿宽系数;δ1、δ2分别为大锥齿轮和小锥齿轮的分度圆的锥角数值。V为锥齿轮副的总体积,V1、V2分别为大锥齿轮和小锥齿轮的体积[4]。
由公式(1)可以得到,制约锥齿轮副总体积的相关参数包括小锥齿轮部件的齿数数值z1、锥齿轮副系统的大端一侧的模数数值m以及锥齿轮的齿宽系数ψR,综上所述,可以对系统的设计变量x进行设置,公式(4)所示。

式中:T为主动小锥齿轮工作时的转矩。
锥齿轮的齿面接触强度的约束条件如公式(5)所示。

式中:g1(x)为锥齿轮的齿面接触强度;[σH]为锥齿轮副系统的齿面部位理论许用接触应力数值;d1为锥齿轮的分度圆直径。
锥齿轮齿根部位的弯曲强度约束条件如公式(6)所示。

式中:g2(x)为齿根弯曲强度;[σF]为锥齿轮副系统的齿根部位理论许用弯曲应力数值;m为复合型齿形系数数值。
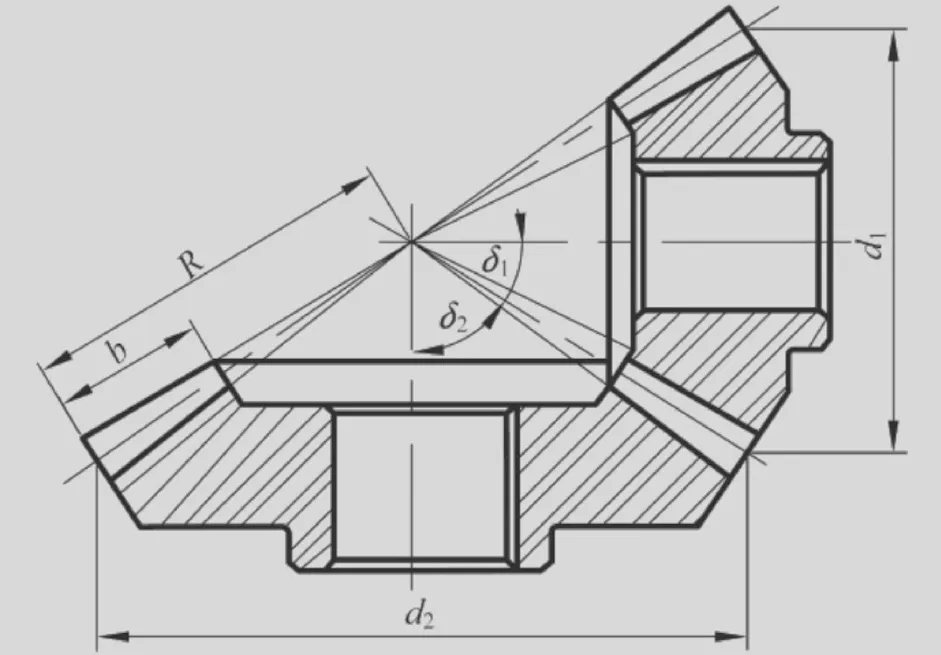
图3 锥齿轮副外形尺寸
针对复合型的齿形系数,能够根据当量的齿数借助图4进行查询。
设计变量的约束条件是:17cosδ1≤z1≤z1max;m≥2;0.25≤ψR≤0.30。
根据上述的数学模型的表达式可知,以锥齿轮副系统的总体积最小为目标的优化设计工作能够总结为1个三维的非线性约束条件的优化改进型问题。
7 锥齿轮系统结构优化设计实际案例简述
已知某汽车的发动机系统传动部分是1套轴交叉角数值为90°的闭合式锥齿轮传动系统机构,小锥齿轮传递的功率数值P1为9.2 kW,转动速度n1取值为970 r/min,系统的传动比i取值为3,工作状态系数K取值为1.5。小锥齿轮部件的材料选用40Cr,采用了调质工艺进行处理,其布氏硬度(HB)数值达到了250。大锥齿轮部件的材料选用35SiMn,西永了调质工艺进行处理,其布氏硬度(HB)数值达到了230。设计要求为使锥齿轮副总体积最小,以此完成整体结构的优化设计过程。

图4 复合齿形因数和当量齿数之间的联系
针对以上相关参数实施总结及运算,能够得出主动轮(小锥齿轮)工作状态下的转矩T1数值为:T1=9550P1/n1=90.6 (N·m)。
根据锥齿轮系统传动机构的金属及材料相关的工艺方面的标准,由相关文献中查询到齿面部分的理论许用接触应力[σH]数值为640 MPa,齿根部分的理论许用弯曲应力[σF]数值为250 MPa。
惩罚型函数方法是一类间接式求解的约束系统优化情况的解决方案,把相关约束问题优化转成一整套0约束的问题来进行方程求解,不会对原有的约束状态造成变更及破坏。该文使用惩罚型函数方法体系中的外点式方法法,将系统的约束相关的非线性设计情况问题转化成1种适应型函数,其公式(7)所示。

式中:val(x)表示该数学模型的惩罚函数;f(x)表示该数学模型的目标函数;p(x)表示惩罚选项。
极小化相关情况如公式(8)所示。

式中:r1、r2为惩罚选项的系数,g1(x)为齿面接触强度、g2(x)表示齿根弯曲强度,是1类伴随迭代次数递增来递增的数列。
将公式(8)中的3D不等式形式的约束非线性目标状态转化成外部点惩罚型函数适应性函数的有关问题,也就是说把优化数学模型的公式(5)、公式(6)中2个约束设置为适应性函数中的惩罚选项,然后把数学模型变量相关边界约束设成遗传式计算方法中的变量矩阵[5]。
中锥齿轮副属于闭合式软齿面传动,配合锥齿轮传动法则,选取锥齿轮的齿面部位接触强度约束的惩罚系数r1=1,齿根部位弯曲强度约束的惩罚系数r2=0.5。
使用MATLAB优化单元fmincon模式,在程序中输入分度圆的直径、锥距、齿数比和目标函数等相关参数。将不等式约束条件作为惩罚选项导入适应型函数。
将最优解导入校验,g1(x)=-0.082 MPa≈0,g2(x)=247.5915 MPa>0,因此最优解处于齿面部位接触强度数值的边界区域,齿根部位弯曲强度裕量较大。
将最优解的小齿轮齿数调整为18,导入校核,g1(x0)=13.5032 MPa>0,g2(x0)=248.6596 MPa>0,因此最优的整数解处在可行区间。
8 结语
综上所述,该文研究了锥齿轮系统传动机构的特点,搭建其数学模型,获取相关结构优化相关变量、目标函数、各项功能限制条件及边界限制状况,并且对锥齿轮传动机构实施改进设计。应用惩罚函数的方法构建适应程度相关函数,将改进设计函数模型中的锥齿轮齿面触碰强度基础及锥齿轮齿根弯曲角度条件转化为适应程度函数公式中的惩罚项。编写遗传算法某种类型的文件,应用MATLAB软件及优化工具模块Fmincon函数实施函数求解,获得最优结果。软件运算完毕之后,还必须针对相关变量参数进行圆整及调节。经过优化案例证明了使用遗传式计算方法实施锥齿轮系统传动机构改进设计的通用性及可行性,为锥齿轮系统传动机构的多重目标改进设计带来了技术参照。因此,对机械锥齿轮传动的进行优化及研究,对科技进步及国民经济的发展具有重大的实用意义。
