部分充填混凝土-钢箱连续组合梁裂缝特征
2021-04-14郑艳王泽博莫时旭蒋越
郑艳, 王泽博, 莫时旭, 蒋越
(1. 桂林理工大学 土木与建筑工程学院, 广西 桂林 541004;2. 桂林理工大学 广西岩土力学与工程重点实验室, 广西 桂林 541004)
混凝土-钢箱连续组合梁桥因其可以发挥钢材与混凝土各自的材料优势,施工便捷及造价较低等优点,被广泛应用到中小跨径桥梁的建设中,但是组合连续梁桥由于支座附近混凝土与钢材皆处于不利的受力状态,为了增大其跨越能力,以及提高其结构的力学性能,一些学者提出了双重组合结构.通过在中支座附近下缘增设混凝土,参与受压,以达到增大跨越能力、降低工程造价、增大结构刚度、调节结构受力分布,以及减小钢板厚度等目的.文献[1-3]在中支座附近的钢箱内部填充混凝土以改善负弯矩区的受力性能,提高结构整体的承载力和刚度.文献[4-12]研究影响组合梁负弯矩区裂缝发展的因素以有效控制其裂缝发展.聂建国等[13]认为综合力比(R)及栓钉间距对组合梁负弯矩区裂缝发展有显著影响,并推导考虑力比和栓钉间距影响的最大裂缝宽度计算公式.文献[14-15]在试验基础上,将横向钢筋间距和力比作为主要影响参数,给出混凝土桥面板的裂缝间距计算公式,并对相关规范中的钢筋应变不均匀系数进行修正.文献[16-18]理论推导组合梁混凝土开裂后截面钢筋的应力计算公式,但对部分充填混凝土-钢箱连续组合梁的试验数据研究有限.
本文通过对5根部分充填混凝土-钢箱连续组合梁进行静力加载试验,研究不同配筋率及抗剪连接度对负弯矩区开裂特征的影响,提出开裂弯矩和裂缝宽度计算公式.
1 试验研究
1.1 试验设计方案
1.1.1 试验梁设计 设计5根部分充填混凝土-钢箱连续的组合梁(PFCSB1~PFCSB5),试件总高度为420 mm,全长为6 400 mm,两端支座外预留长度为200 mm.钢梁选用Q235级钢板,由厚度为10 mm、宽度为220 mm的顶板和底板,以及厚度为6 mm、高度为300 mm的腹板共同焊接而成.将厚度为6 mm的Q235级钢板作为水平隔板,将试验梁负弯矩区域的钢箱分为上、下箱室,并在下箱室充填C40混凝土,充填高度为137 mm.试验梁构造图,如图1所示.

(a) 纵截面图

(b) 中支座截面图 (c) 跨中截面图图1 试验梁构造图(单位:mm)Fig.1 Structure of test beam (unit: mm)
剪力连接件采用Φ12、长100 mm的栓钉,梁翼板采用HRB400级纵向钢筋,HPB300级横向钢筋,所有试件跨中配筋率均为1%.5个试验梁均为同一批混凝土浇筑.连续梁试件参数表,如表1所示.表1中:p为负弯矩区栓钉间距.
钢材材料特性表,如表2所示.表2中:h为钢板厚度;Es为弹性模量;fs为极限抗拉强度;fy为屈服强度.翼板采用C40混凝土,截面尺寸为1 000 mm×120 mm,混凝土材料特性表,如表3所示.表3中:fcu为标准立方体抗压强度.

表1 连续梁试件参数表Tab.1 Parameters of continuous beam specimen

表2 钢材材料特性表Tab.2 Steel material performances

表3 混凝土材料特性表Tab.3 Concrete material performances
1.1.2 试验加载装置及测量系统 两跨连续试验梁中支座采用固定铰支座,边支座采用可调移动铰支座,利用油压千斤顶在试验梁跨中点加载.千斤顶上放置压力传感器,监测每级施加的荷载值,支座安放压力传感器测定支座反力.试件加载装置图,如图2所示.试验初裂阶段,每级荷载为20 kN,待首条贯通裂缝产生后,将每级荷载增大至40 kN.
用记号笔将混凝土面板划分成间距为100 mm的方格网,便于迅速标注裂缝的位置及发展.每级加载结束后,待持荷稳定,记录裂缝发展长度,并用裂缝观测仪读取裂缝宽度.
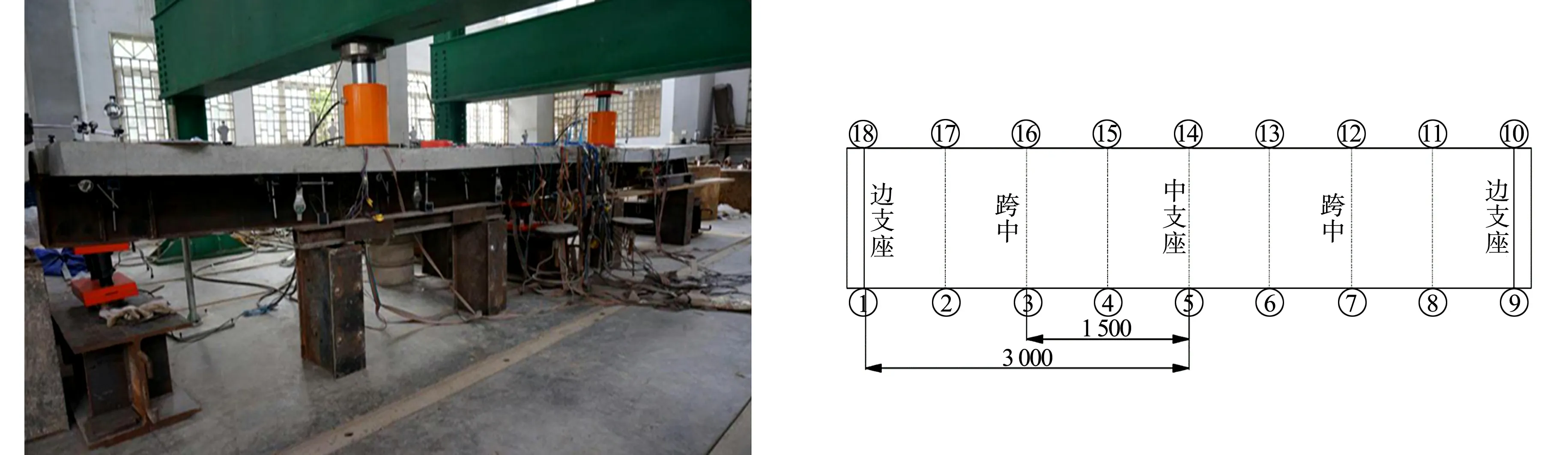
图2 试件加载装置图 图3 连续组合梁挠度测定布置图(单位:mm) Fig.2 Loading device of specimen Fig.3 Deflection measurements of continuous composite beams (unit: mm)
混凝土面板及混凝土翼板钢筋应力测点布置图,分别如图4,5所示.
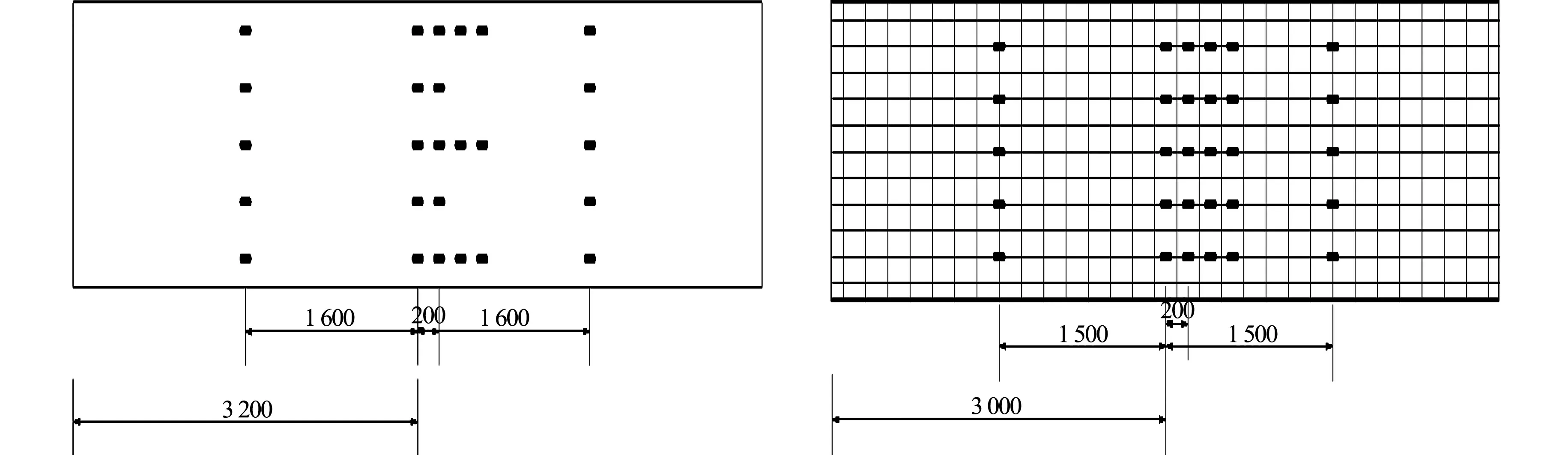
图4 混凝土面板测点布置图(单位:mm) 图5 混凝土翼板钢筋应变测点布置图(单位:mm) Fig.4 Loading device of specimen Fig.5 Arrangement of strain measuring points for concrete panel (unit: mm) reinforcement of concrete flange (unit: mm)
1.2 试验梁受力过程

图6 试验梁荷载-挠度图Fig.6 Load-deflection relationship of test beams
试验梁荷载-挠度图,如图6所示.图6中:P为荷载;f为挠度.
由图6可知:试验梁整个受力过程分为3个阶段.第1阶段为弹性工作阶段,该阶段为试验梁从加载至钢箱底板屈服前,荷载-挠度近似直线关系;第2阶段为弹塑性工作阶段,钢箱底板开始屈服,组合梁刚度降低,挠度的增加速率明显高于荷载的增加速率,跨中截面内力重分布程度加大;第3阶段为塑性破坏阶段,跨中钢箱腹板逐渐屈服,组合梁混凝土翼板塑性中和轴高度上升,混凝土底板、侧板的开裂宽度加深.在试验梁达到极限承载力前,正弯矩区的钢箱腹板出现斜向凹凸屈曲波,破坏时,承载力则取决于混凝土顶板极限压应力和钢箱底板极限抗拉强度.
1.3 裂缝特征
试验梁各阶段裂缝分布图,如图7所示.

(a) 试件PFSCB1
由图7可知:第一条裂缝出现在组合梁中支座附近翼板中间区,随着荷载的持续增加,并向翼板边缘延伸,当荷载为200 kN左右时,在翼板顶面出现横向贯通裂缝;随着荷载的继续增加,横向裂缝由中支座向跨中发展,逐渐形成多条横向贯通的裂缝,间隔为80~150 mm;当荷载超过600 kN,在已贯通的裂缝之间出现一些短小的次裂缝;在近跨中位置,受加载点局部应力影响常产生C字形裂缝;随着荷载的持续增加,主裂缝宽度随着受拉钢筋的屈服迅速增大,配筋率最大的PFSCB3与其他梁相比,裂缝分布更为均匀和密集.
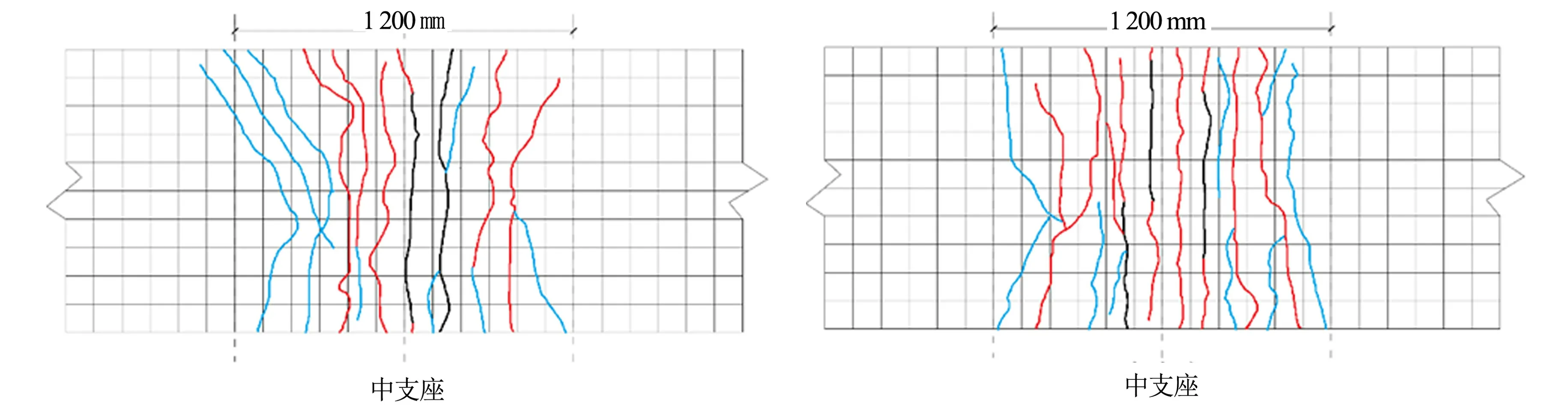
(b) 试件PFSCB2 (c) 试件PFSCB3

(d) 试件PFSCB4 (e) 试件PFSCB5图7 试验梁裂缝分布图Fig.7 Crack distributions of test beams
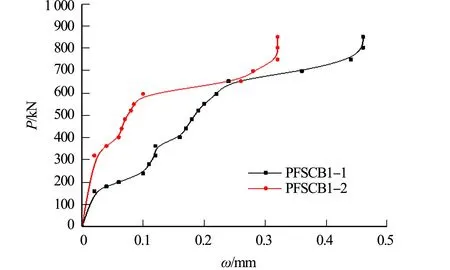
(a) PFSCB1

(b) PFSCB2 (c) PFSCB3

(d) PFSCB4 (e) PFSCB5图8 试验梁荷载-裂缝关系图Fig.8 Load-crack relationship of test beams
试验梁荷载-裂缝关系图,如图8所示.图8中:ω为裂缝宽度.
由图8(c)可知:PFSCB3的3条主要裂缝宽度发展相对比较均匀,裂缝宽度增大较缓慢,最大裂缝宽度达到0.2 mm时,荷载已达到1 000 kN,可见配筋率提高可以有效控制裂缝发展.
综上分析,组合梁在全受力过程中负弯矩区翼板裂缝的发展大致呈现4个阶段的特点.
第1阶段为初裂阶段,在到达极限承载力约15%左右时,试验梁均在中支座板中心附近出现第1条裂缝,在到达极限承载力约20%时,第1条裂缝横向贯通.
第2阶段为裂缝均匀增加阶段,荷载在极限承载力的20%~60%阶段,翼板裂缝由中支座向跨中等间距发展,逐渐产生多条横向贯通裂缝.
第3阶段为裂缝加密阶段,荷载增加至极限荷载的60%以后,在贯通横向裂缝间产生次级加密裂缝.
第4阶段为裂缝宽度快速增长阶段,此时,组合进入承载力极限状态,梁变形快速增大,翼板不再产生新的裂缝,主要的裂缝宽度开始剧烈扩展,直至组合梁破坏.

图9 试验梁中支座混凝土面板荷载-应变图Fig.9 Load-strain relationship of bearing concrete slab of test beams
2 试验结果分析
2.1 开裂弯矩
通过记录翼板应变片数据随加载等级的变化,可以准确得出混凝土面板的开裂荷载,进而计算试验梁中支座截面实测开裂弯矩.试验梁的中支座混凝土翼板荷载-应变曲线,如图9所示.图9中:εc为混凝土面板的应变值.
由图9可知:曲线的首个转折点即为混凝土翼板开裂后,裂缝两侧混凝土翼板局部卸载,导致邻近裂缝的应变片记录的应变略有下降;试验梁PFSCB1~PFSCB5的开裂荷载分别为120,139,160,143,147 kN左右,这与试验过程中裂缝观测记录的试验梁开裂荷载基本吻合.
羊海林等[19]综合考虑混凝土抗拉强度、收缩应力及截面特征,推导出的负弯矩区混凝土面板的开裂弯矩计算公式为
Mc,r=(γscft-σcs)W′,
(1)
W′=Ics/y,
(2)
(3)
(4)


表4 开裂弯矩计算值与试验值Tab.4 Calculated values and experimental results of cracking-moment
由于试验梁PFSCB2,PFSCB4,PFSCB5的配筋率与其他截面特性相同,故其开裂弯矩理论值计算结果相同,在此只用PFSCB2进行比较.
2.2 综合力比对裂缝开展的影响
综合考虑配筋率和钢箱的共同作用,可以更好地了解组合结构的裂缝开展特征.用综合力比R表示组合梁负弯矩区截面的物理性能,即
(5)
式(5)中:Ar与fry分别为负弯矩区截面受拉钢筋的截面积与屈服强度;As与fy分别为钢梁的截面积和屈服强度;Ac与fc为钢梁内填充混凝土的截面积与屈服强度.
各试验梁裂缝特征数值,如表5所示.表5中:l为平均裂缝间距;ω为裂缝宽度.
通过混凝土面板应变数据的突变点可以准确得到各试验梁的开裂荷载.PFSCB1中支座负弯矩区共有8条可观测的裂缝,缝有两条,宽度分别为0.46,0.32 mm.其中,贯通裂PFSCB2在负弯矩区共产生9条可被观测的裂缝,最大裂缝宽度为0.38 mm. 相比PFSCB1, PFSCB2混凝土面板的裂缝宽度发展较为缓慢.PFSCB1~ PFSCB3荷载-裂缝宽度对比图,如图10所示.

表5 各试验梁裂缝特征数值Tab.5 Crack characteristics value of every test beam

图10 PFSCB1~PFSCB3荷载-裂缝宽度对比图Fig.10 Load-crack width comparison of PFSCB1-PFSCB3
由图10可知:虽然裂缝宽度增长缓慢,但PFSCB2在加载过程中产生了更多微小裂缝,裂缝密度也明显大于PFSCB1;PFSCB3在负弯矩区一共产生了8条可被观测的裂缝,其中的3条贯通裂缝的宽度分别为0.26,0.34,0.26 mm;PFSCB3的裂缝宽度发展速率大致与PFSCB2相近,但是纯弯段的裂缝宽度明显小于PFSCB2,在钢筋受拉的阶段裂缝发展在各试验梁中最为缓慢.
PFSCB1的R在所有试件中最小,裂缝发展特征与少筋梁的十分类似.当可观测的裂缝出现时,受拉钢筋随即屈服,裂缝宽度急剧增加,但是很少有细微裂缝产生,因此,其裂缝间距和裂缝宽度都偏大.由于钢梁的共同作用,使全梁的延性提高,导致其并未呈现明显的脆性破坏特征.随着R的增加,PFSCB2与PFSCB3的裂缝宽度增加的速度明显小于PFSCB1,且拥有更小的裂缝宽度与更大的裂缝密度.通过对裂缝产生荷载的分析研究,发现PFSCB1在300~400 kN的加载阶段,有6条裂缝出现.R相对较大的PFSCB2,PFSCB3梁裂缝的产生基本与加载等级呈现线性关系,即随着荷载的增大裂缝逐条产生,未发现裂缝在某一等级阶段集中出现的现象,可得出R较大的试验梁具有更大的刚度.
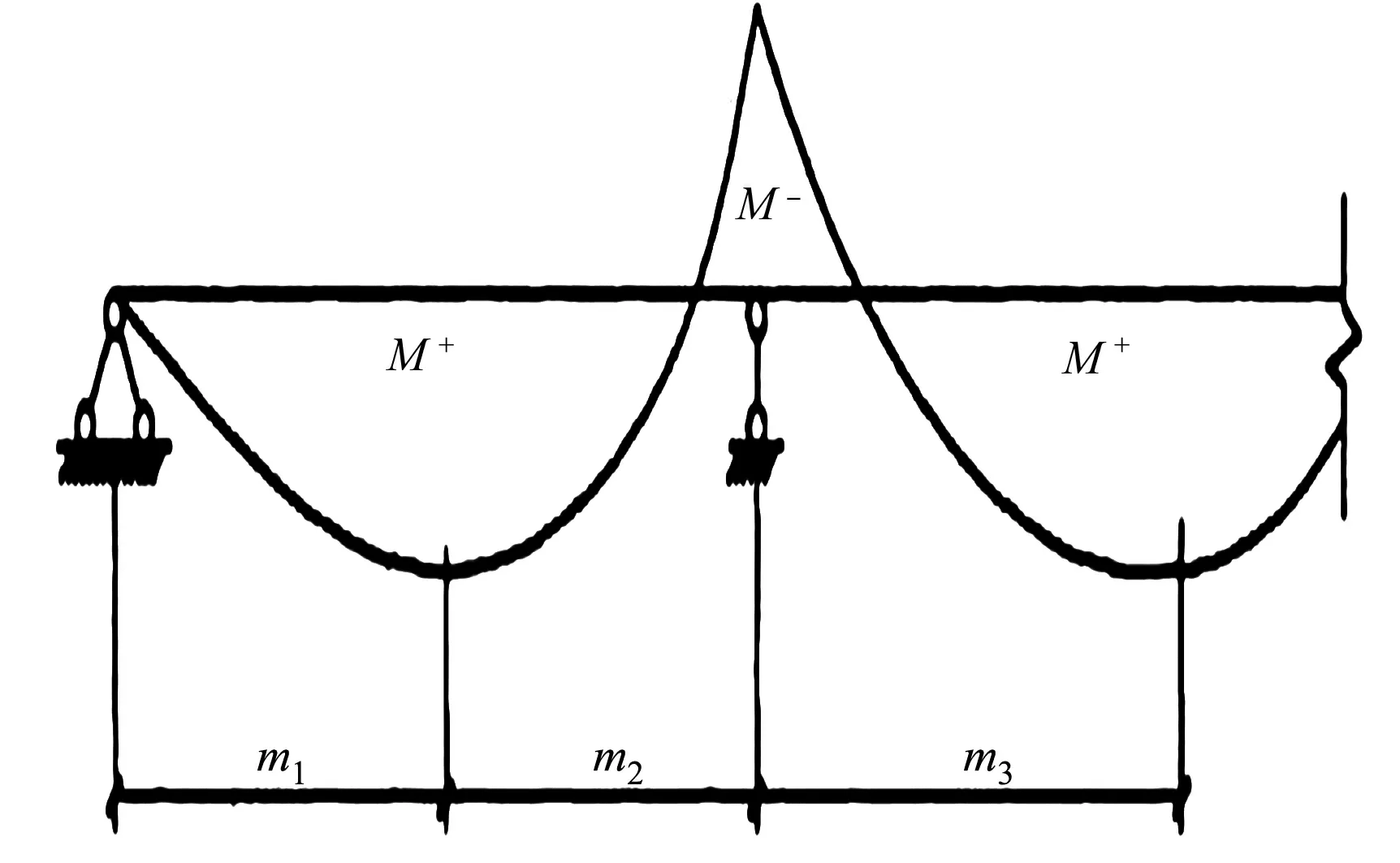
图11 连续梁剪跨区划分图Fig.11 Shear-span area of continuous beam
综上所述,综合R对部分充填混凝土-钢箱连续组合梁中支座区混凝土翼板裂缝宽度及开裂荷载均影响较大.适当提高中支座区的配筋率可以在提高开裂弯矩的同时,降低最大裂缝宽度.通过对裂缝密度及裂缝间距的分析,可以看出R对裂缝的分布和开展也有一定的影响,R较大的试验梁拥有更大的开裂荷载、更慢的裂缝发展速度及更小的裂缝间距.
2.3 栓钉间距对裂缝发展的影响
连续梁剪跨区划分图,如图11所示.图11中:M+,M-分别为连续梁的正弯矩区和负弯矩区;m1为正弯矩最大点到边支座区段;m2,m3为正弯矩最大点到中支座区段.抗剪连接件作为组合梁的重要组成部分之一,在受力过程中的作用是传递剪力.组合梁负弯矩区混凝土受拉易开裂,而混凝土开裂退出工作后,纵向钢筋则承受了大部分拉应力,钢筋的拉应力又通过混凝土传递给栓钉.由于栓钉的抗剪强度较大,进而抑制混凝土面板裂缝宽度的发展.当采用柔性抗剪连接件时,抗剪连接件的计算应以弯矩绝对值最大点及支座为界限.
当组合梁按完全抗剪连接设计时,每个剪跨区段内需要的连接件总数nf为
nf=Vs/Ncv.
(6)
式(6)中:Vs为每个剪跨区段内钢梁与混凝土翼板交界面的纵向剪力;Ncv为单个抗剪连接件的受剪承载力设计值.部分抗剪连接组合梁连接件实配个数不得少于nf的50%,文中PFSCB4与PFSCB5各剪跨区段内实配连接件的个数分别为0.5nf与0.75nf.
通过设计三根配筋率相同但抗剪连接度不同的试验梁分析栓钉间距对中支座负弯矩区裂缝发展的影响.PFSCB2,PFSCB5,PFSCB4试件中支座区栓钉间距分别为81.0,107.0,166.6 mm.栓钉间距对裂缝分布和平均裂缝间距的影响,如表6所示.表6中:rc为开裂范围.
由表6可知:随着栓钉间距的减小,裂缝平均间距及开裂范围也随之减小,且裂缝平均间距与栓钉间距十分相近.在裂缝分布范围内,绝大部分栓钉上都有开裂现象.这是因为开裂截面处,钢筋应变由于栓钉受到限制,钢筋的拉力通过混凝土传给栓钉,引起栓钉上方混凝土处的应力集中,尤其当裂缝开展较大时,连接件的作用更为明显.栓钉间距越小的试验梁产生的裂缝受到的限制越大,越能促进新裂缝的产生.除此之外,随着栓钉间距的减小,组合梁翼板内次生弯矩分布也相对更均匀一些,所以裂缝平均间距和最大裂缝宽度也随之减小.

表6 栓钉间距对裂缝分布和平均裂缝间距的影响Tab.6 Influence of stud spacing on crack distribution and average crack spacing
3 裂缝宽度计算
文献[13]考虑力比和栓钉间距的影响,建议组合梁最大裂缝的计算式为
ωmax=1.45ψεrLcr,
(7)
(8)
(9)
式(7)~(9)中:εr为钢筋拉应变;d为钢筋直径;p为栓钉连接件间距;C为最外层纵向受拉钢筋外边缘至受拉区底边的距离;v为纵向受拉钢筋表面特征系数,选取v=0.7;μct=Ar/(bchc),bc,hc分别表示混凝土翼缘有效宽度和厚度.
文献[14]将横向钢筋间距和配筋力比作为重要影响参数,建议的连续组合梁桥面板最大裂缝计算公式为
(10)
式(10)中:la为横向钢筋平均间距.
PFSCB1~PFSCB5的弹性极限荷载为Py,翼板顶面裂缝贯通后荷载达到0.8Py和Py时,试验梁翼板裂缝宽度,如表7,8所示.表7,8中:ω0.8Py为荷载等级0.8Py时的最大裂缝宽度实测值;ωp为弹性极限状态试验梁最大裂缝宽度实测值;ω1,ω2分别对应式(7),(10)计算所得的最大裂缝宽度.
由表7,8可知:文献[14]所得的计算结果与试验值相差较大,而文献[13]由于综合考虑钢箱-混凝土组合梁的R、栓钉间距对裂缝宽度的影响,计算结果和试验值更为接近,对裂缝最大宽度的计算具有一定的参考意义.
为研究钢梁内有无填充混凝土对弹性阶段内连续组合梁混凝土翼板裂缝宽度的影响,采用文献[13]的公式计算无填充混凝土-钢箱连续组合梁在弹性阶段内的翼板最大裂缝宽度,并与部分填充混凝土钢箱连续组合梁的最大裂缝宽度进行对比.有、无填充混凝土连续组合梁翼板裂缝宽度对比,如表9所示.表9中:ω3与ω5分别为部分填充混凝土连续组合梁在0.8Py与Py荷载等级下的最大裂缝宽度计算值;ω4与ω6分别为无填充混凝土连续组合梁在0.8Py与Py荷载等级下的最大裂缝宽度计算值.

表7 P=0.8Py时试验梁翼板裂缝宽度Tab.7 Crack widths of test beams when P=0.8Py

表8 P=0.8Py时试验梁翼板裂缝宽度Tab.8 Crack widths of test beams when P=0.8Py

表9 有、无填充混凝土连续组合梁翼板裂缝宽度对比Tab.9 Comparison of flange crack width of continuous composite beam with and without concrete filling
由表9可知:在弹性阶段内,部分填充混凝土钢箱连续组合梁的最大裂缝宽度计算值小于无填充混凝土连续组合梁的计算值.这主要由于钢梁内填充混凝土提高了中支座负弯矩区截面的抗弯刚度,使得部分填充混凝土钢箱连续梁受拉钢筋的拉应力小于同一荷载等级下无填充混凝土连续梁的受拉钢筋.
4 结论
1) 部分充填混凝土-钢箱连续组合梁负弯矩区配筋率配筋率提高,裂缝密度增大,裂缝宽度增大减缓,当组合梁负弯矩区配筋率为1.0%,1.5%,2.0%时,对应试验梁弹性极限荷载时的裂缝宽度分别为0.24,0.22,0.14 mm,组合梁负弯矩区翼板配筋率对裂缝控制作用明显.
2) 当裂缝开展较大时,栓钉可以有效限制裂缝宽度的进一步增加,转而促进更多次生裂缝的产生.
3) 考虑混凝土收缩应力影响和组合截面塑性系数,计算开裂弯矩与试验结果吻合良好,当组合梁负弯矩区配筋率为1.0%,1.5%,2.0%时,对应试验梁的开裂弯矩分别为78.13,80.52,81.69 kN·m,表明混凝土翼板配筋率提高对开裂弯矩的影响不大.
4) 部分充填混凝土-钢箱组合梁弹性工作阶段混凝土翼板最大裂缝宽度的计算应综合考虑组合梁的配筋率、力比、栓钉间距及钢箱内混凝土填充度的影响.
