两挡变速器换挡过程最优控制的伪谱法求解*

刘晓坤，赵鑫鑫

（北京科技大学机械工程学院，北京 100083）

前言

当前国内关于新能源汽车的研究主要是纯电动汽车，采用固定挡位的汽车存在着电机效率低下、动力不足的情况，且转速转矩传递效果不好，大大浪费了在行驶过程中的电量。如果采用较大功率的电动机，则会发热较为严重，降低了电机的使用寿命。在纯电动汽车的开发与设计过程中，需要兼顾动力性和经济性，选择合适的驱动电机和传动装置，两者能够相互匹配，充分提高其运行性能。考虑到汽车传动系统的布置空间有限，为了保障其最佳运行性能，采用两挡或者多挡变速装置能有效利用电机的高效区域，有利于提高车辆行驶的动力性与经济性［1］。

在变速器换挡最优控制方案设计的过程中，需要基于现代控制理论、优化概念，以变速器换挡过程作为优化对象，减小动力中断时间，确保转矩输出的平稳变化。考虑到离合器滑摩功、换挡冲击度、主从动盘的转速差等多个问题，需采取有效控制措施，保障换挡过程中的动态平衡。

文献［2］中对并联混合动力车辆AMT 不分离离合器换挡过程进行了研究，深入分析了换挡各个阶段中影响换挡时间、零部件寿命以及换挡冲击的因素。文献［3］中在换挡协同控制中采用了电机主动调速换挡的控制方法，降低并联混合动力汽车AMT换挡过程产生的冲击。文献［4］中对一种装有组合式湿式离合器/制动器的两挡行星齿轮式变速器的换挡过程电机协调控制策略进行了仿真研究。文献［5］中以双电机混合动力系统为研究对象，通过协调控制动力源的输出转矩以及执行机构的工作状态，实现了无动力中断换挡。文献［6］中对采用轮毂电机作为动力装置的两轮独立驱动电动汽车的驱动控制进行了研究。

伪谱法属于最优控制问题的数值解法，因其收敛性好，计算效率高，适合本文中两挡变速器换挡过程最优控制问题的求解。

伪谱法求解最优控制问题的一般步骤［7］如下：

（1）选择合适的正交多项式系，在其作用域的正交配点上，将连续函数离散为有限的离散点集；

（2）利用谱微分矩阵与正交求积公式，在离散点集上表达最优控制问题，形成非线性规划问题；

（3）采用常用的序列二次规划（SQP）算法直接求解非线性规划（NLP）问题；

（4）在非线性规划问题解（离散点集）上，通过最佳逼近理论获得原最优控制问题的解。

伪谱法的正交配点由基底函数和正交求积方法决定，可以将伪谱法细分为Radau 伪谱法、Legendre伪谱法、Gauss 伪谱法和Chebyshev 伪谱法。Radau伪谱法因其在处理连续时间最优控制问题上具有优势，以及具有结构简单、指数收敛速度快、精度较高等特点得到了快速发展。因此，本文中采用Radau伪谱法求解两挡变速器换挡过程最优控制轨迹。

1 两挡变速器建模

1.1 两挡变速器的结构

本文中研究的两挡变速器的基本结构是并联双排行星齿轮机构，其两个单排行星齿轮机构均为单级行星齿轮机构。并联关系中，一级太阳轮与二级太阳轮相连，一级行星架与二级齿圈相连，用S 代表太阳轮，R 代表齿圈，C 代表行星架，P 代表行星轮，整个变速器属于典型的辛普森式CR-SS 型变速器。一二级太阳轮S1S2 与驱动电机相连，一级齿圈R1由制动器B2 制动，二级齿圈R2 由制动器B1 制动，二级行星架C2 连接主减速器。整个系统由S1S2 输入，由换挡机构控制B1 和B2 的制动与分离，由C2输出动力。该两挡变速器结构简图和三维渲染图如图1和图2所示，各部件名称如表1所示。

图1 变速器结构简图

图2 两挡变速器三维结构图

1.2 两挡变速器的换挡工作原理

两挡变速器的换挡机构由换挡电机、蜗杆、带有楔形块的蜗轮、2 个螺旋曲面导引机构和钢片、摩擦片组成。换挡机构的电机通过底座连接在两挡变速器的外壳体上，经联轴器将动力输入到蜗杆上。蜗杆通过外壳体的轴承支撑，将动力传递到蜗轮上。蜗轮的两侧是通过螺栓连接直接固定在壳体上的螺旋引导机构，蜗轮的旋转经螺旋引导机构的限位，分别压紧两侧的摩擦片，实现行星轮系齿圈的制动和放松。挡位信息如表2 所示（++表示接合，--表示分离）。

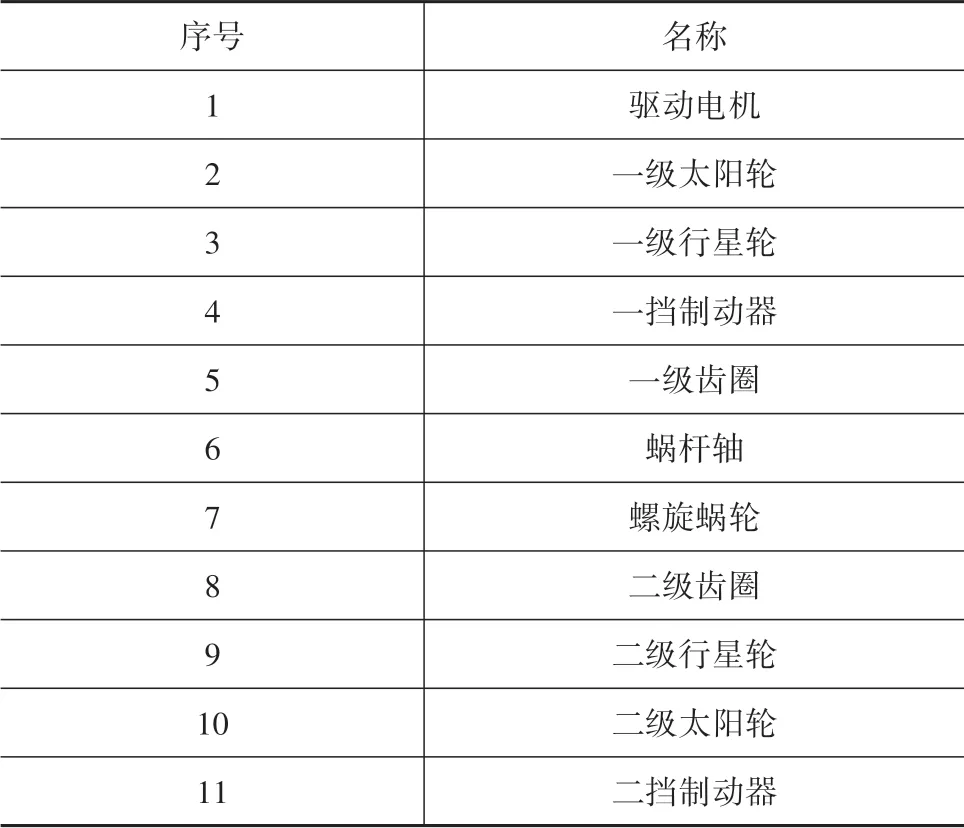
表1 两挡变速器结构部件

表2 两挡变速器挡位信息

蜗轮蜗杆换挡机构可提供一个很大的减速比，且拥有自锁功能，在制动器完成接合之后，换挡电机无需再提供转矩来防止制动器放松，消除了换挡电机由于长时间堵转导致电机烧毁的可能。在换挡时，只需控制换挡电机的正反转，使蜗轮产生轴向位移，分别压紧两侧的离合器片，即可实现挡位的切换。

由两挡变速器的结构形式和换挡电机的工作原理可得到3 个阶段换挡过程，分别为：现接合挡位的制动器分离-空行程阶段-将接合挡位的制动器接合。由于车辆本身的惯性影响，驱动电机和负载之间的转矩不同，制动器分离和接合过快会导致车辆出现顿挫感，影响换挡品质。空行程阶段关系着系统的动力输出，应尽量减小，整个换挡过程3 个阶段应遵循慢-快-慢的规律，具体情况如图3所示。

图3 换挡过程转矩转速变化（以升挡为例）

1.3 两挡变速器动力学模型建立

目前对行星式齿轮变速器的主流建模方法可分为两类：基于运动学建模和基于动力学建模。基于运动学的建模方法通常有杠杆法、能量法、相对速度法和图解法；基于动力学的建模方法通常有拉格朗日法、功率键合图法、运动学分析和静力分析法等。本文中选取的两挡变速器结构较为简单，采用较为简单的杠杆法来建立两挡变速器的动力学模型。

杠杆模拟法是Benrord和Leising在文献［8］中提出的用杠杆模拟行星轮系的分析方法。对于单行星齿轮系统，可以运用等效杠杆法将其等效为具有3个节点的杠杆［9］，由文献［10］中可知，等效杠杆法中行星轮系和模拟杠杆的对应关系如表3所示。

表3 等效杠杆法的对应关系

本文中研究的两挡变速器为2 自由度系统，系统中任何1 个构件的角速度ωj都可以由任意选定的2个基准构件A、B的角速度ωA、ωB进行线性表示。

式中：α、β为速度表出系数，其大小由j点到A、B 两点的距离决定，当位于两点之间时α、β均为正，当位于A 点之外时β为负，位于B 点之外时α为负。α、β的具体图示与表达式如图4与式（2）所示。

图4 速度表出系数示意图

对等效杠杆来说，两挡变速器各构件的角速度与基准构件的角速度关系即为各节点的速度vj与基准点的速度vA、vB的线性关系：

等效杠杆的静力学平衡充要条件为

式中Fj为杠杆上各点受到的外力。

在换挡过程的动力学分析中，行星轮也有转动惯量，需要将这部分能量考虑其中，因此在变速器杠杆法的建模中，需要把行星轮放在杠杆之上。

在单级行星齿轮系统之中，行星轮与太阳轮直接相连，随行星架绕太阳轮公转和自身自转，为了简便计算，其等效转动惯量为

式中：Jp'为行星轮的等效转动惯量；Jp为行星轮自转转动惯量；rp为行星轮公转半径；mp为行星轮的质量。

在等效之后，行星轮只有自转，其与太阳轮之间的速比就可以确定。

式中：ZS为太阳轮齿数；ZP为行星轮齿数。

两挡变速器的结构是两级行星排，分别遵循各自的杠杆原理，但在整体研究时，需要将分杠杆图进行合并，合并时保证各节点之间的力臂比例与分杠杆图中的比例相同即可［11］。在合并时，选择将S1C1 的力臂长度进行放大，放大系数K=(ZR2+ZS2)/ZR1，将行星轮与齿圈之间的力臂长度记为ZL=ZS(ZR/ZP- 1)，这样就可以将两个分杠杆图进行合并得到总杠杆图，变换过程如图5 和图6 所示，总杠杆转矩示意如图7所示。

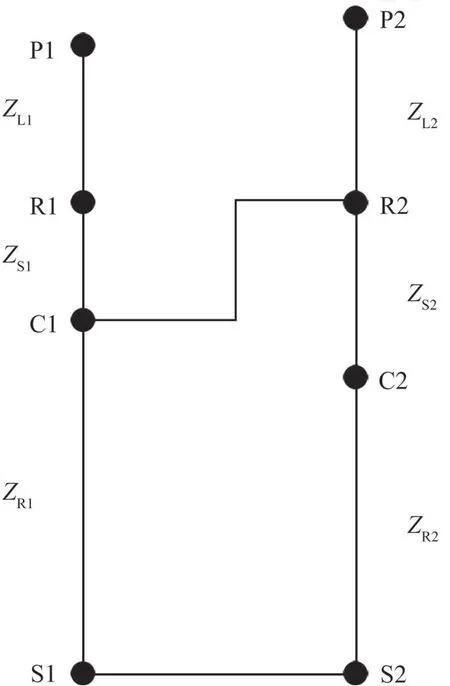
图5 两挡变速器分杠杆图

图6 两挡变速器总杠杆图

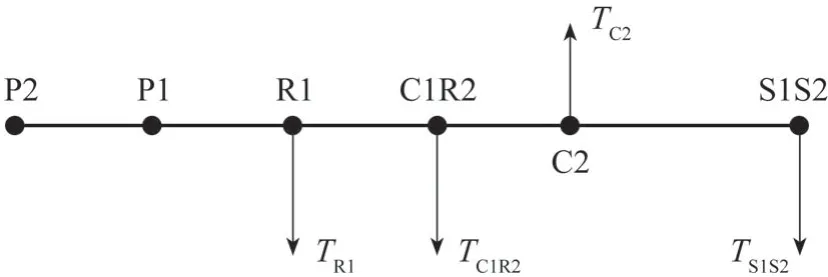
图7 两挡变速器总杠杆转矩示意图

选择S1S2 和C2 作为基准构件，分别令ωS1S2和ωC2等于0 和1，根据杠杆中各支点之间的力臂长度，得到各构件相对于基准件的角速度表出关系（见图8和表4）。

通过角速度表出关系，得到了变速器中各构件与基准构件之间的角速度关系。在杠杆的静力平衡方程式的基础上，运用达朗贝尔原理，即可以得到模拟杠杆的动力学运动方程：

式中：mj为j点等效后的质量；aj为j点等效后的加速度。

图8 两挡变速器角速度表出关系图

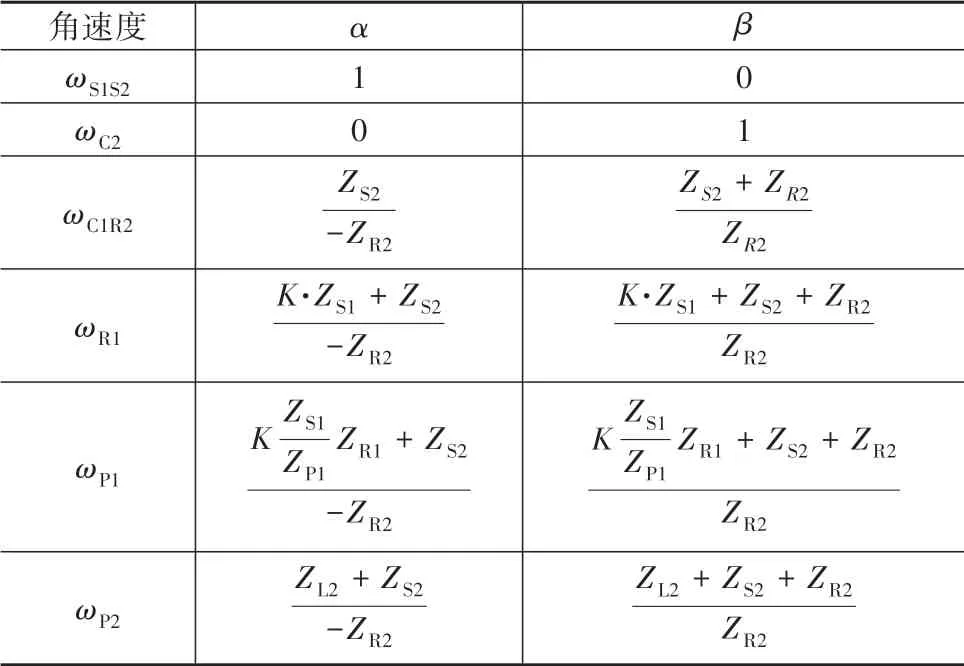
表4 角速度表出关系

根据行星轮系和模拟杠杆之间的对应关系，由式（7）得到本文中所使用的两挡变速器的动力学运动方程：

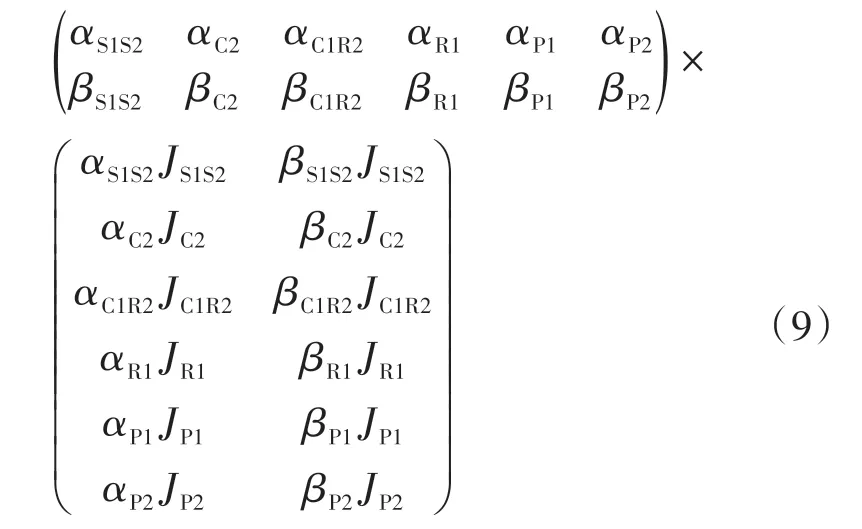
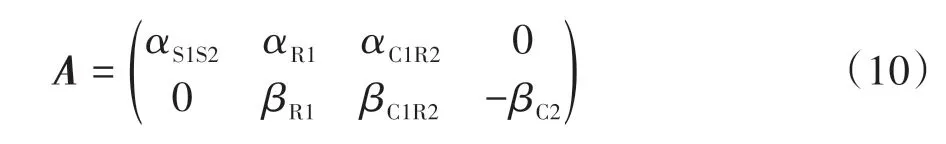
式中：J为由表出系数α、β和各构件转动惯量组成的系数矩阵；A为由角速度表出系数组成的矩阵；T为两挡变速器各构件传递的转矩。

由两挡变速器结构决定的转矩对应关系如表5所示。

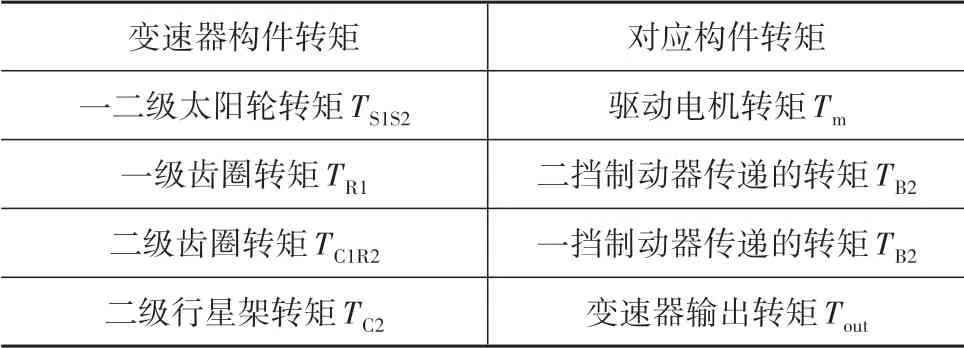
表5 两挡变速器转矩对应关系

由表5 的对应关系可得到整个变速器的动力学模型表达式：

2 两挡变速器换挡过程最优控制问题

根据文献［12］，本文中将双离合器联合起步过程的优化控制问题归结为一个最优控制问题并进行求解。选取发动机转矩变化率和离合器转矩变化率作为控制变量，以滑摩功和冲击度平方为性能指标，在满足状态方程、终端约束和过程约束条件下求解最优控制规律。

2.1 状态方程

（1）状态变量的选取

选择驱动电机输出轴转速ωm、变速器输出轴转速ωv、制动器主动片的转速ωR2和ωR1、驱动电机转矩Tm、制动器传递的转矩TB2和TB1作为状态变量。

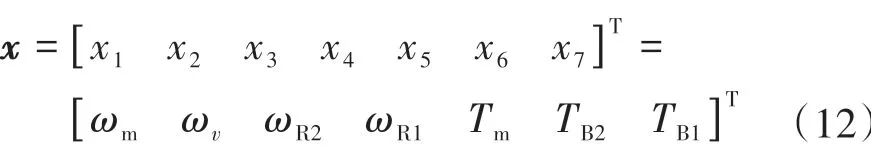
（2）控制变量的选取

在由等效杠杆法建立的整车动力学方程中，电机的输入转矩、制动器传递转矩和整车负载转矩直接影响了换挡过程中两挡变速器的响应，因此在换挡过程中，着重关注驱动电机和制动器的转矩变化情况，选择驱动电机的转矩变化率T˙m、制动器的转矩变化率T˙B2和T˙B1作为控制变量。

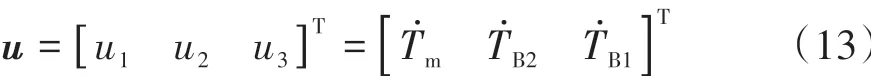
（3）系统的状态方程

系统的状态方程由状态变量和控制变量组成：

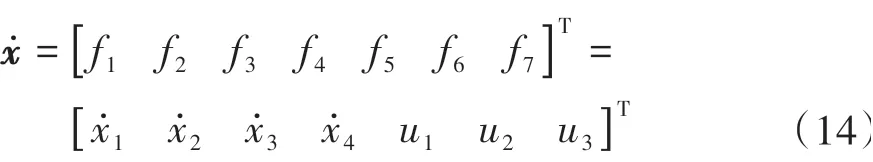
根据建立的两挡变速器动力学模型，可得到

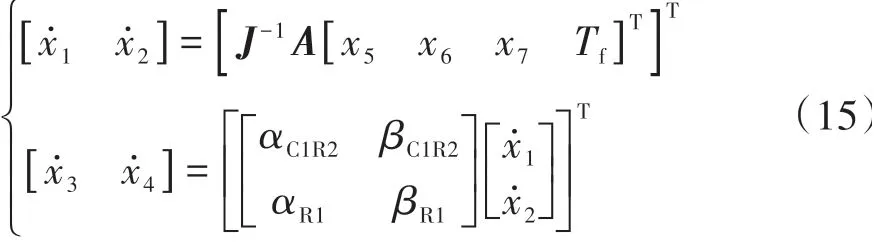
因此整个系统的状态方程为

2.2 评价函数

换挡品质客观评价指标包括冲击度、换挡时间和滑摩功［13］。冲击度［14］用来表征汽车纵向速度的变化情况，在一定程度上体现了换挡过程的平顺性。对于装有自动变速器的汽车，换挡过程的平顺性显得更为重要。使用冲击度作为换挡品质评价指标，不仅可以避免道路条件和驾驶员等非换挡因素的影响，更能真实反映换挡时变速器输出轴转矩的扰动情况，这与驾驶员和乘客的主观感受一致。

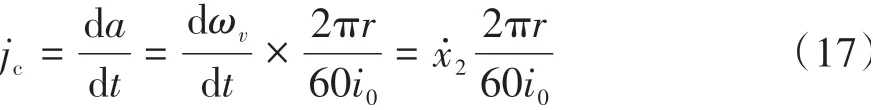
式中：a为汽车行驶的纵向加速度；r为车轮半径；i0为主减速比；ωv为变速器输出转速。

为了表征换挡过程中冲击度，取冲击度的平方作为优化目标。

滑摩功［15］是计算离合器主从动片接合过程中摩擦做功的多少。在滑摩过程中，离合器的主从动片由于其转速不同产生摩擦，离合器的温度随之上升，若滑摩时间过长，会导致摩擦片过度磨损，甚至导致制动失效。因此滑摩功的大小可以代表离合器的使用寿命，滑摩功越小，离合器主从动片之间的磨耗就越小，离合器的使用寿命就会越长。

由两挡变速器结构决定的制动器从动摩擦片转速为0，因此在换挡过程中，滑摩功来自于制动器主动片，即两挡变速器两级行星排的齿圈，表达式为

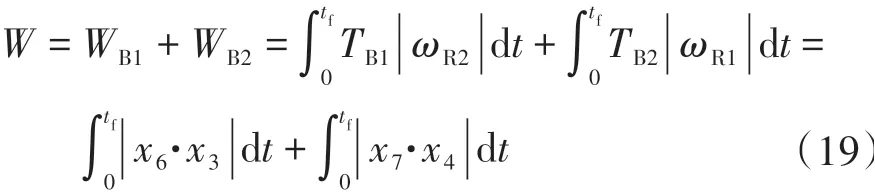
式中：tf为换挡完成时间；TB为离合器传递的转矩；ωR为两级行星排齿圈的转速，即离合器主动片的转速。

通过分析可知，在换挡过程中若想获得较好的平顺性，要求离合器尽可能缓慢接合，减小冲击度。而与此同时带来的结果是离合器接合的时间变长，滑摩所产生的热量增多，不利于保护离合器。由此可见，冲击度和换挡时间/滑摩功是相互矛盾的目标。因此需要设计合理的换挡控制策略来权衡这些控制目标，从而达到提高换挡品质的目的［16］，因此采用换挡品质综合评价指标，引入权重系数λ(0 ＜λ＜1)，通过调整权重系数实现对冲击度和滑摩功进行权衡。

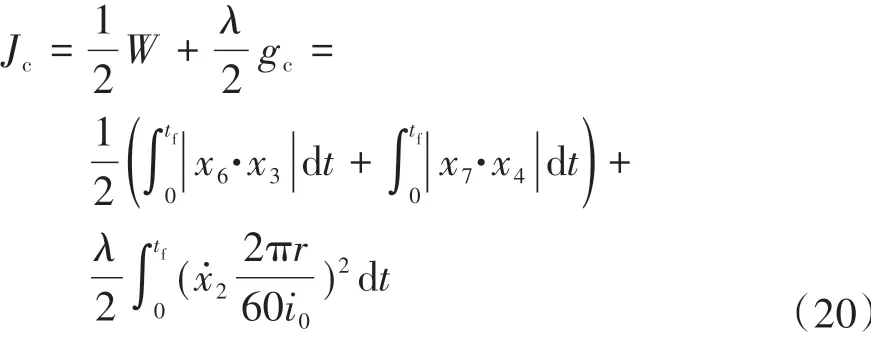
2.3 约束集

在两挡变速器换挡过程的最优控制问题中，整个过程分为3 个阶段：制动器分离阶段、空行程阶段、制动器结合阶段，用p= 1，2，3 表示3 个阶段，3个阶段的起始和终止时间分别用t=t0，t1，t2，tf表示。

2.3.1 过程约束

（1）驱动电机转速约束

驱动电机的转速与很多因素有关，电机所能达到的最高转速是有一定限度的，因此驱动电机的转速约束为

将此约束表示为C1(x1(t)，t) ≤0。

（2）驱动电机的转矩变化率和制动器的转矩变化率约束

将此约束表示为C2(u(t)，t) ≤0。

（3）制动器转矩约束

制动器传递的最大转矩是由换挡电机控制的换挡机构压紧离合片产生的，是一个确定的值，而其实际传递的转矩是由变速器的工作状态决定的，与滑动摩擦力和最大静摩擦力的关系相似。

以升挡过程为例，制动器接合二级齿圈，一级齿圈不传递转矩，处于空转状态，升挡完成后，一级齿圈接合，二级齿圈因与一级行星架相连，其传递的转矩为一级行星架的转矩，非因制动器接合而产生的转矩，故不作约束。升挡过程的约束为

降挡过程的转矩传递与升挡过程相同，其制动器转矩约束也相同，只需将时间阶段对调即可。

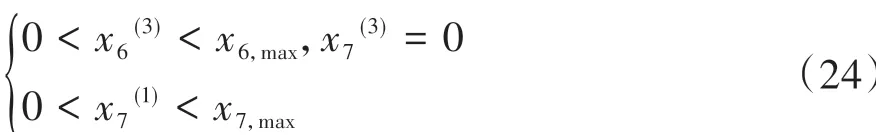
将不等式约束表示为C3(x6(t)，x7(t)，t) ≤0，等式约束表示为φ4(x7(t)，t) = 0。

2.3.2 终端约束

（1）变速器转速约束

在换挡开始之前和结束之后，变速器均处在制动器完全制动的状态，整个变速器遵循自己的动力方程进行传动，变速器的输入输出转速存在固定关系。

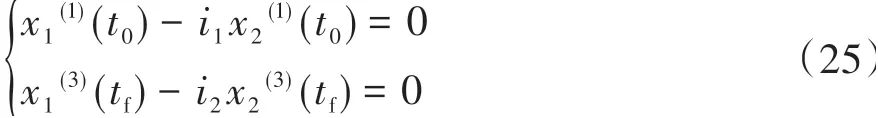
将此约束表示为φ1(x1(t)，x2(t)，t) = 0。

（2）制动器转速约束

两挡变速器的结构设计中，摩擦片主动片的一侧是两级行星齿轮机构的齿圈，从动片均固定在两挡变速器的壳体上，其转速为0，制动器的转速约束实际上为两级行星齿轮机构齿圈的转速约束。制动器的转速约束与制动器的转矩约束类似，同样以升挡过程为例，二级齿圈释放过程中，其转速由0 开始逐渐增大，在经历过滑摩状态后，制动器完全释放二级齿圈。在一级齿圈接合并完全制动时，其转速由空转逐渐减小，经过滑摩状态后被完全制动，因此升挡过程中制动器主动片的转速约束为

降挡过程的转速约束与升挡过程相同，也只需将时间阶段对调即可。

将此约束表示为φ2(x3(t)，x4(t)，t) = 0

（3）变速器输出轴转速约束

换挡机构采用反应灵敏、效率高的无刷直流电机，换挡过程用时很短，假定车速没有产生变化，即变速器的输出轴转速在换挡前后保持不变。

将此约束表示为φ3(x2(t)，t) = 0。

2.4 两挡变速器换挡过程最优控制问题描述

根据对两挡变速器换挡过程的分析，其换挡过程可以由以下方程描述。

3 换挡过程最优控制问题的伪谱法求解过程

Radau 伪谱法将状态变量和控制变量分别离散后，利用Lagrange 插值多项式逼近状态和控制变量，将状态方程的微分运算和性能函数中的积分运算均转化为代数运算，最终将最优控制问题（OCP）转化为以节点处的状态变量、配点处的控制变量为待优化参量的非线性规划问题（NLP），选用成熟的NLP问题求解器进行计算，得到两挡变速器换挡过程的最优控制律。伪谱法通常包含时域变换、配点与离散化和状态方程与性能函数的转化3个部分。

3.1 时域变换

伪谱法的配点分布在［-1，1］上，在使用伪谱法时需要分别将3 个阶段的时域从变化到［-1，1］上，使其满足Legendre 正交多项式的定义区间，其变换过程为

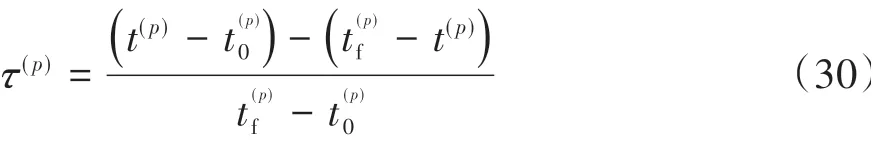
式中：p= 1，2，3代表换挡过程的3个阶段；和代表p阶段的起止时间。

3.2 配点与离散化

Radau 伪谱法的配点采用LGR（Legendre-Gauss-Radau）配点，即基底函数采用Legendre正交多项式，正交求积方法采用Gauss-Radau 求积方法。除各阶段的首尾配点和是确定的外，其余N-1 个的配点是N阶Legendre 正交多项式1 阶导数的 根，等 价 于 多 项 式的 根，N阶Legendre正交多项式为

在得到每个阶段的N+1 个配点后，每个阶段的状态变量和控制变量就可以进行离散化，用N+1 阶Lagrange插值多项式近似逼近：

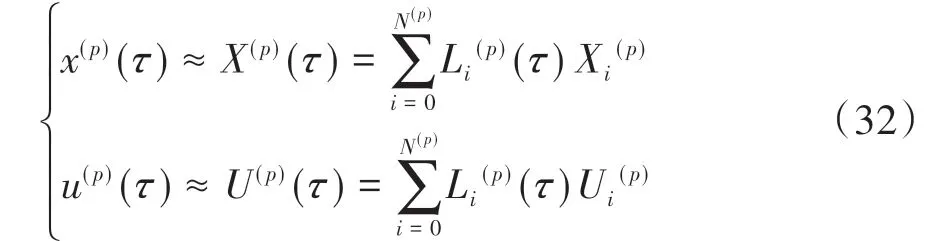
N+1阶Lagrange插值基函数为

3.3 状态方程与性能函数的转化

利用离散化之后的状态变量和控制变量，状态方程可通过Lagrange多项式的1阶导数表示。

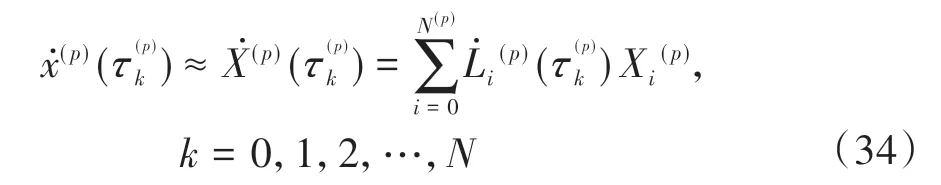
(p)(τk)表示Lagrange 插值基函数的微分矩阵，其具体表达形式参照文献［17］。

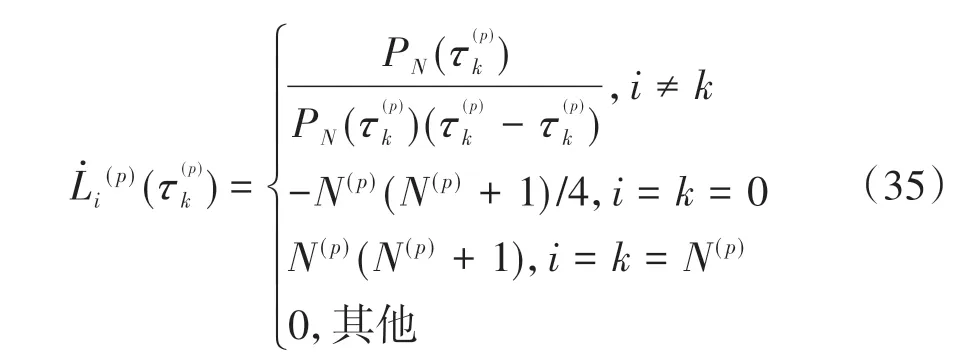
由此可以将状态方程约束转换成各阶段在N+1个配点处的等式约束。

经过前面步骤的离散化后，性能指标中的Lagrange 项的积分计算可通过Gauss-Radau 积分方法转化为对N+1 个节点处的Lagrange 项的求和运算，其转化形式为

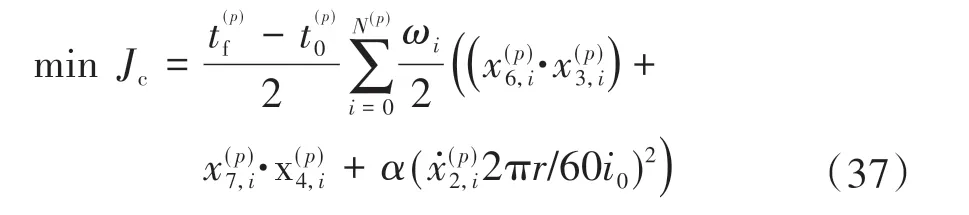
ωi为积分权重，表达式为

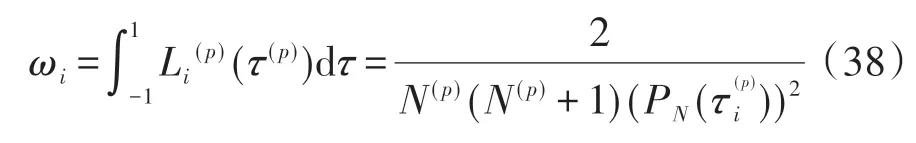
3.4 最优控制问题转化为非线性规划问题

通过以上对最优控制问题的转换，就可以将两挡变速器换挡过程最优控制问题用非线性规划问题的形式描述。

上述非线性规划问题本质上是一个高维稀疏问题，采用成熟的GPOPS求解器［18-19］进行求解运算，从而得到两挡变速器换挡过程最优控制问题的最优状态变量轨迹和最优控制变量轨迹。

4 换挡过程仿真结果

本文中两挡变速器电动汽车的主要参数如表6所示，利用GPOPS 求解器求解两挡变速器在升挡和降挡过程中的最优控制轨迹。

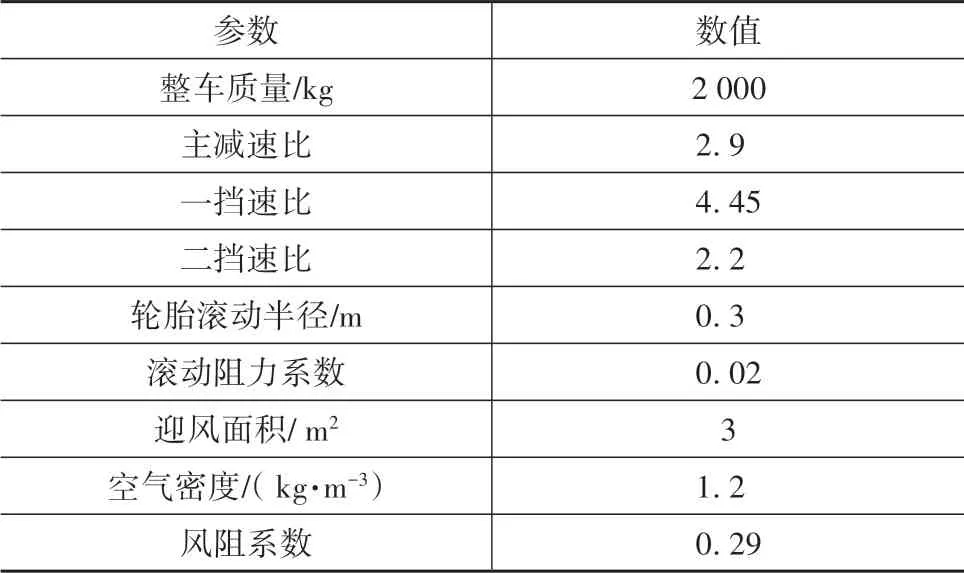
表6 两挡变速器的电动汽车主要参数

4.1 不同评价指标下换挡过程仿真验证

选择只考虑冲击度和同时考虑冲击度滑摩功两种情况进行升挡仿真验证，车辆在平地加速行驶，当驱动电机转速达到3 000 r/min 时进行升挡操作，升挡完成后，驱动电机仍以相同的驱动转矩继续驱动车辆进行加速。仿真得到的两种情况下冲击度和滑摩功的结果如图9和图10所示。

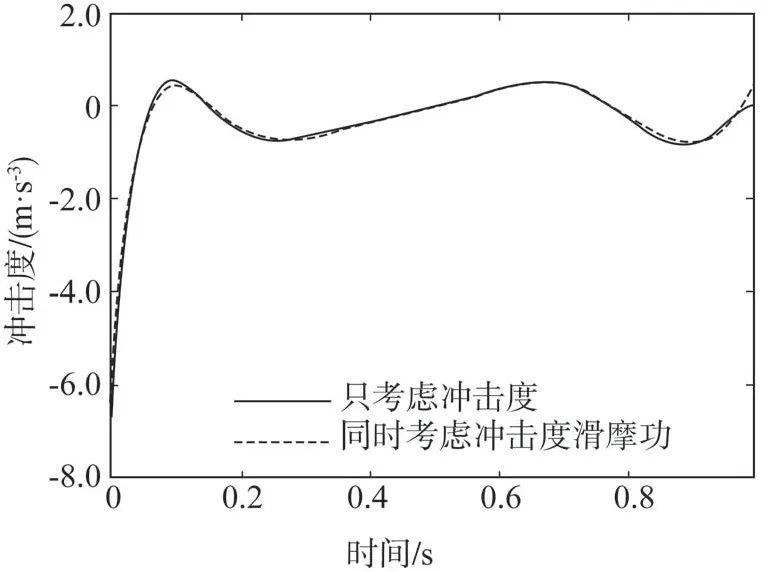
图9 升挡过程冲击度变化

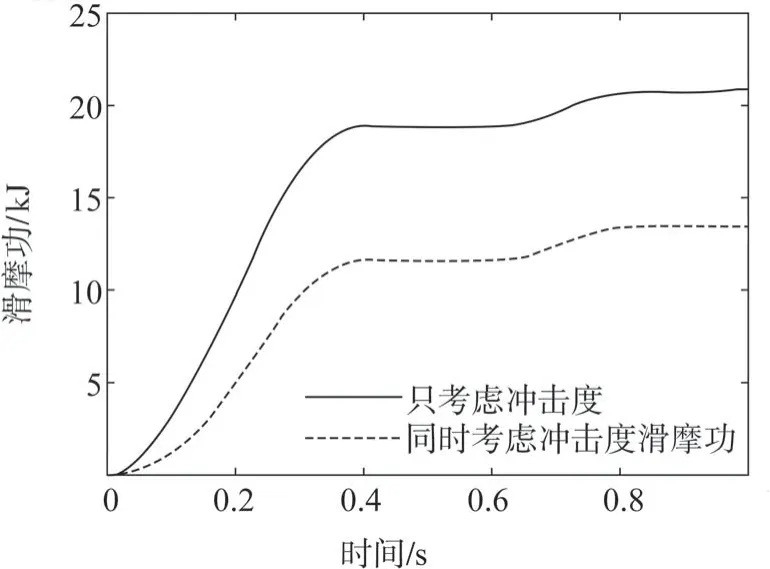
图10 升挡过程滑摩功变化

从仿真结果对比可知，同时考虑冲击度和滑摩功的情况较只考虑冲击度，滑摩功从20.94 减小为13.5 kJ，减小了约35.5%。滑摩功与制动器主动片的转速和制动器传递的转矩有关。由图11 可知，在一挡制动器分离时，同时考虑冲击度滑摩功的情况下，一挡制动器主动片的转速比只考虑冲击度的情况低，使得一挡制动器分离时产生的滑摩功更小；而在二挡制动器接合时，二者相差不大，滑摩功也相当。

图11 升挡过程制动器主动片转速变化

4.2 伪谱法与二次型仿真验证

为验证伪谱法在变速器换挡过程中的有效性，在降挡过程中，采用了伪谱法和二次型两种方法同时进行求解，其结果如图12和图13所示。

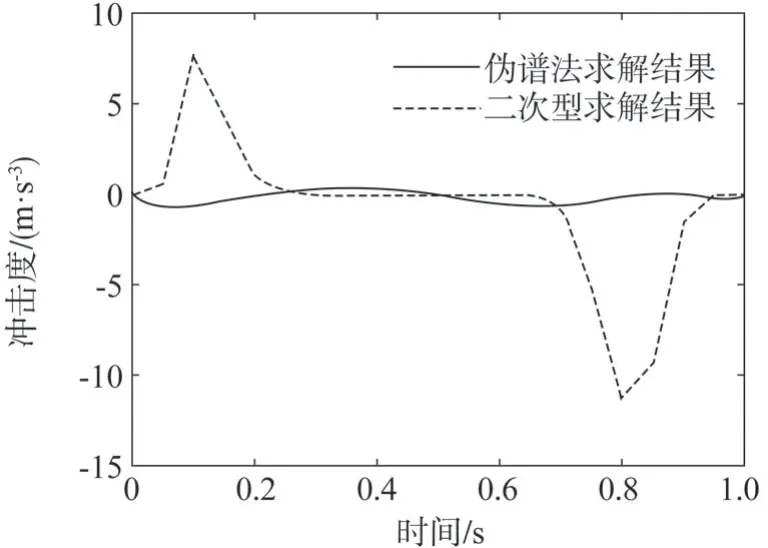
图12 冲击度变化

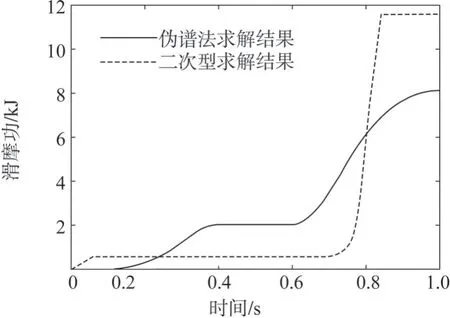
图13 滑摩功变化

二次型得到的两挡变速器降挡过程结果，冲击度在-11.2～7.7 m/s3之间，滑摩功为11.6 kJ。伪谱法求得的降挡过程的冲击度在-0.67～0.39 m/s3之间，相较于二次型求解的结果，冲击度更小更平滑；滑摩功为8.08 kJ，相较于二次型求得的结果减小了约28%。

5 结论

在本文中，利用等效杠杆法建立了两挡变速器的动力学模型，选择了换挡冲击度和离合器滑摩功作为两挡变速器换挡品质的评价函数，研究了两挡变速器换挡过程最优控制问题的状态方程和约束条件。以驱动电机和两个制动器的转矩为控制变量，以冲击度和滑摩功为性能指标，采用Radau 伪谱法将两挡变速器换挡过程的最优控制问题经时域变换、参数离散化、函数转化等过程转化为非线性规划问题，并在求解器中求得了两挡变速器换挡的最优控制轨迹。

基于某型采用该两挡变速器的电动车参数，对求得的两挡变速器换挡的最优控制轨迹进行仿真验证，同时对伪谱法和二次型求解的结果进行对比验证，仿真结果验证了最优控制轨迹的有效性，也同时验证了Radau 伪谱法在求解多阶段带边界约束的最优控制问题的有效性和便捷性。