变尺寸装箱问题的迭代/贪婪动态规划算法

姚汝林，尹石军，郭蕴华

(1.上海交通大学 船舶海洋与建筑工程学院，上海 200240; 2.招商局重工(江苏)有限公司，江苏 海门 226116；3.武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

0 引言

管材切割是船舶建造过程中的一个重要的生产步骤，新近研究将船厂管材切割问题描述为一维下料问题(One-dimensional cutting stock problem，1D-CSP)[1]。但是，由于船舶建造的复杂性，某些场合零件管和原料管都具有随机长度。在此情况下，应将船舶建造的管材切割问题描述为变尺寸装箱问题(Variable-sized bin packing problem，VSBPP)，而非1D-CSP[2]。对于VSBPP问题，研究人员先后提出了近似算法[3]、分支定界算法[4]、分组遗传算法(Grouped genetic algorithm, GGA)[5]、迭代递减首次适合算法(Iterative first-fit decreasing, IFFD)[6]、迭代MBS启发式算法(Iterative minimal bin slack, IMBS)[7]、可变邻域搜索(Variable neighborhood search,VNS)方法[8]和基于动态规划的启发式方法[9]进行求解。

上述方法在优化计算花费和剩余长度等方面都取得了一些进展。但是，船舶建造的管材切割化问题是VSBPP的特殊变体，其VSBPP问题(VSBPP of pipe-cutting in ship-building，VSBPP_PS)与经典VSBPP有所不同。第一，上述大多数算法都假定箱子的长度类型是有限的，而每种类型的供应都是无限的。这些假设与船舶建造中的一些管材切割实例恰好相反。在船舶建造的实际生产情况中，经常遇到的情形是箱子(原料管)和物品(零件管)的长度是随机的。第二，很多文献都涉及基于动态规划来解决背包问题的方法。动态规划的时间复杂度为O(l·n)[10]，其中：l为箱子的长度，n为物品数。然而造船厂的切割精度为“mm”，即使对于6 m的原料管，l也等于6 000 mm。对于动态规划而言，船厂的大多数原料管都是“超长”的。更为不利的是每根原料管的长度都不同，需要对所有原料管执行动态规划进行试算。由此可见，如果将纯动态规划的方法直接用于求解船厂的管材切割问题，其计算成本是难以忍受的。

针对上述船舶建造中VSBPP_PS问题在实际应用方面的困难，本文提出一种迭代贪婪/动态规划算法(Iterative greedy/dynamic programming，IGDP)对其求解。通过贪婪/动态规划组合解法求解子集和问题(Subset sum problem，SSP)，并应用这一方法实现对整个VSBPP_PS问题的构造启发式求解。为了进一步提高求解质量，采用迭代的“拆箱/再分配”方法实现局部搜索。

1 问题描述

令I=(1,2,…,n)和J=(1,2,…,m)分别表示零件管集合和原料管集合，且零件管i和原料管j的长度为vi和lj。定义决策变量y=(y1,y2,…,ym)，∀j∈J，若原料管j被选中则yj=1，否则yj=0。定义决策变量xij，∀i∈I，∀j∈J，若零件管i从原料管j上切割，则xij=1，否则xij=0。于是，VSBPP_PS可以描述为

(1)

s.t.Rj≥0

(2)

(3)

xij∈{0,1},∀i∈I,∀j∈J

(4)

yj∈{0,1},∀j∈J

(5)

式中的Rj为原料管j切割后的剩余长度，它可以由下式计算：

(6)

目标函数式(1)的含义为最小化所有被选原料管的总剩余长度；约束条件式(2)确保所有被选中原料管在切割后的余长≥0；约束条件式(3)确保每一个零件管只能从一根原料管上切割；约束式(4)～式(5)表明所有决策变量必须是0或者1。

2 迭代贪婪/动态规划算法

为了求解式(1)～式(6)所描述的VSBPP_PS问题，本文提出了一种迭代贪婪/动态规划算法。该算法首先考虑对SSP问题进行贪婪/动态规划组合求解，然后对其进行调用实现对整个VSBPP_PS的构造启发式求解。为了进一步提高求解质量，还采用迭代的“拆箱/再分配”方法实现局部搜索。算法几个部分的具体描述如下。

2.1 贪婪/动态规划组合解法

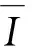
(7)

(8)

式(7)～式(8)所描述的SSP问题可以通过动态规划求得最优解[10]。但造船厂的切割精度是“mm”，因此lj是一个很大的数。对于原料管j，经典动态规划具有时间复杂度O(lj·n)。就船厂的实际应用而言，其计算成本太大。为此，本文提出了贪婪/动态规划组合解法。

Step 2 执行贪婪操作：

Ifcj-vi>vminthen

End If

End for

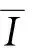
(9)

(10)

(11)

xij∈{0,1},∀i∈I,∀j∈J

2.2 求解VSBPP_PS的构造启发式方法

基于上述贪婪/动态规划组合解法，可以对整个VSBPP_PS实现构造启发式求解，其伪代码如下：

2.3 拆箱/再分配方法

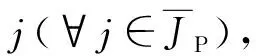
Rj>Tth

(12)

或者

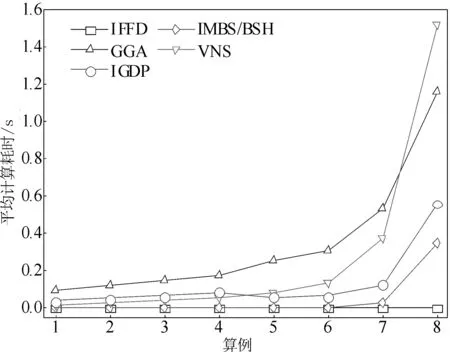
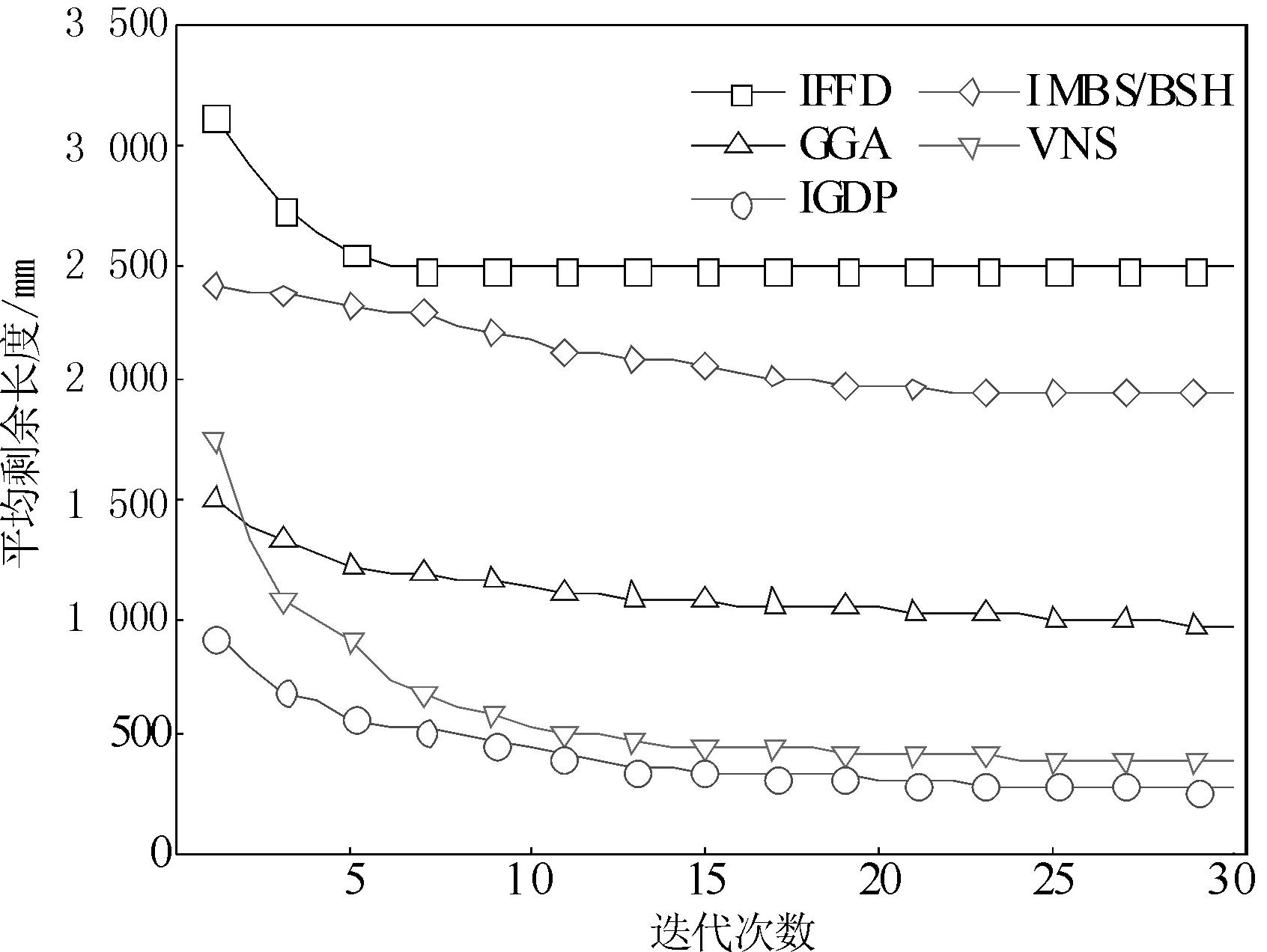
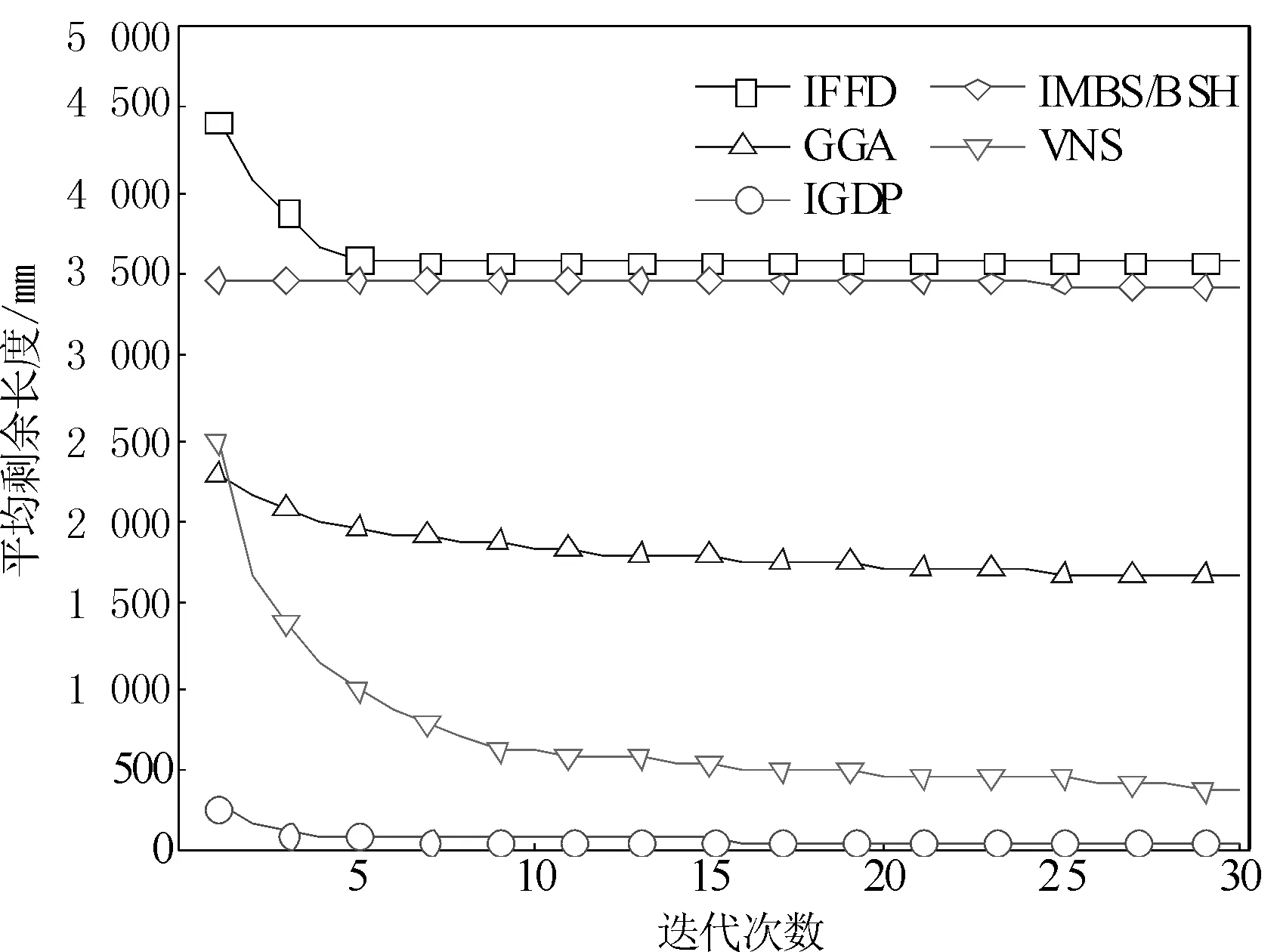
r

(13)

在对当前解中部分原料管进行拆箱操作之后，执行2.2中的Step2～Step5完成再分配。若再分配后得到结果好于当前解则取而代之，否则保留当前解。拆箱/再分配可以反复迭代多次，以提高局部搜索的性能。

3 实验结果与分析

3.1 实验条件

通过对某在建船舶的实际切管订单的总结归纳，设计了8个算例对所提IGDP算法进行了验证，并将其与IFFD[6]、IMBS/BSH[7]、GGA[5]和VNS[8]等现有算法进行了对比分析。现有算法的迭代次数统一设置为30。GGA的种群规模设置为100。IGDP中，Tth=5 mm，Pa=0.05，拆箱/再分配的次数为30。所有算法都用C++编程实现。实验在Intel i7-6 500U 2.5 GHz笔记本计算机上进行。

8个算例中：零件管数量分别为100、120、140、160、180、200、300和500，原料管数量为零件管数量的50%～60%。零件管长度为100～4 000 mm(对于算例1～4，其中：100～500 mm占15%，500～3 000 mm占70%，3 000～4 000 mm占15%；算例5～8中：100～500 mm占20%，500～3 000 mm占60%，3 000～4 000 mm占20%)，原料管长度在2 000～6 500 mm之间。为了降低实验结果对特定算例的敏感性，实验重复100次，且每一次实验中的算例随机生成。

3.2 结果分析

实验结果见图1～图4和表1。其中：图1和图2分别给出了8个算例的所有算法的平均剩余长度和平均计算耗时，图3和图4分别为算例4和算例8的迭代结果图，表1给出了所有算法剩余长度的最小值、最大值、平均值和平均计算耗时。

图1 各算例的平均剩余长度

图2 各算例的平均计算耗时

图3 算例4的迭代结果

图4 算例8的迭代结果

从实验结果可以看出：

(1)对于所有算例，IGDP得到的平均剩余长度均小于现有算法，且表现十分稳定。此外，随着零件管数量的增加，IFFD、IMBS/BSH和GGA的优化性能会有所降低，而VNS和IGDP的优化性能受求解规模影响不大。

(2)由图3和图4可见，随着迭代次数的增加，所有算法的性能均有不同程度的提高。IGDP算法在第1代就具有明显优势，表明基于贪婪/动态规划的构造启发式求解十分有效。并且，随着拆箱/再分配的迭代次数增加，还能进一步提高求解质量。

表1 实验结果

(3)尽管IFFD和IMBS/BSH的计算成本极低，但与其他3种算法相比，它们只能提供勉强满意的性能。前者可以在1 ms内求解任何算例，而后者可以相对较大的计算耗费获得稍好的结果。

(4)在GGA、VNS和IGDP这3个算法中，多数算例中GGA的计算耗费最大，但其优化性能最差。对于算例1～4，VNS的计算耗费小于IGDP的计算耗费；而对于算例5～8，IGDP的计算耗费更少。总体而言，IGDP的计算耗费是可以接受的，便于在实际工程中使用。

4 结语

船舶建造的管材切割化问题是VSBPP的特殊变体。考虑到大多数零件管和原料管具有随机长度，本文提出了IGDP算法。首先，基于贪婪操作和动态规划，实现了对整个问题的构造启发式求解。其次，通过迭代的“拆箱/再分配”操作，改善了算法的局部搜索能力。通过若干计算实例的比较实验，本文提供了充分的证据，证明所提算法优于现有多数算法，并且具有可接受的计算耗费。后续工作将推广本文算法到求解船舶建造中的板材套料、堆场管理等2D-VSBPP或者3D-VSBPP问题，以进一步降低造船成本。