优化初始聚类中心选择的K-means算法

杨一帆 贺国先 李永定

摘要：K-means算法的聚类效果与初始聚类中心的选择以及数据中的孤立点有很大关联，具有很强的不确定性。针对这个缺点，提出了一种优化初始聚类中心选择的K-means算法。该算法考虑数据集的分布情况，将样本点分为孤立点、低密度点和核心点，之后剔除孤立点与低密度点，在核心点中选取初始聚类中心，孤立点不参与聚类过程中各类样本均值的计算。按照距离最近原则将孤立点分配到相应类中完成整个算法。实验结果表明，改进的K-means算法能提高聚类的准确率，减少迭代次数，得到更好的聚类结果。

关键词：聚类;K-means;最近邻点密度;初始聚类中心;孤立点

Abstract：The clustering effect of K-means algorithm is closely related to the selection of initial clustering center and the isolated points in the data， so it has strong uncertainty.In order to solve this problem， a novel K-means algorithm based on nearest neighbor density is proposed. In this algorithm， considering the distribution of the data set， the sample points are divided into isolated points， low density points and core points， and then the isolated points and low density points are eliminated， and the initial clustering center is selected in the core points. Isolated points do not participate in the calculation of the mean value of all kinds of samples in the process of clustering. The outlier is assigned to the corresponding class according to the nearest principle to complete the whole algorithm. The experimental results show that the improved K-means algorithm can improve the clustering accuracy， reduce the number of iterations， and get better clustering results.

Key words： clustering; k-means; nearest neighbor density; initial clustering center; isolated points

聚类就是按一定的标准把物理或抽象对象的集合分成若干类别的过程，聚类后得到的每一个簇中的对象要尽可能的相似，不同簇中的对象尽量的相异[1-2]。聚类分析是一种无指导的学习方式，作为数据挖掘的一个重要研究方向，被广泛应用到商务智能、图像识别、Web搜索等领域。到目前为止，已经形成了很多聚类分析的方法，例如：基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法等等[3]。

K-means聚类算法是数据挖掘中应用最广泛的算法之一[4]。该算法易于实现，收敛速度快，处理数据集时有较好的伸缩性。但是该算法在开始运行时初始聚类中心的选取是随机的，如果初始聚类中心随机选在了数据中的孤立点，那么最后的聚类效果就不会很理想。因此如何选取合适的聚类中心从而避免孤立点的影响一直以来都是K-means算法的一个重要研究方向。很多学者都针对K-means算法的缺点提出了改进策略，例如：冯波等人把最小生成树算法与K-means算法相结合，改进了初始聚类中心的选择方法，提高了聚类的精度[5];邢长征等人提出了基于平均密度优化初始聚类中心的K-means算法[6]，利用事先定义的密度参数与平均密度删除孤立点然后从剩余的点中挑选初始的聚类中心，缩小了聚类中心选取的范围，节省了时间;金晓民等人結合层次聚类与最小生成树的思想提出了一种基于最小生成树的多层次k-Means聚类算法[7]，并将其运用到了数据挖掘中，提高了挖掘的效率;赵文聪等人提出了一种新的基于影响空间的快速K-means算法[8]，在保证聚类精度的同时提高了聚类的效率;胡伟[9]结合空间层次结构，提出一种改进的层次 K均值聚类算法，最后的聚类效果较好，但是算法消耗的时间较长。本文在前人研究的基础上，围绕K-means算法受初始聚类中心的选取与孤立点影响较大的缺点进行研究。结合最近邻的思想，提出了一种优化初始聚类中心选择的K-means算法，实验结果表明，改进的算法迭代次数更少，准确率更高。

1 K-means算法的一般步骤

K-means聚类算法首先随机选取k个样本点作为初始聚类中心，计算各个数据与所选聚类中心的距离[10]，按距离最近的原则将各个样本点分配到相应的簇中，通过计算每个簇的均值，找到新的聚类中心，进行迭代，直到满足收敛条件，算法结束。

2 基于最近邻点密度的K-means算法

2.1 算法的思想

K-means算法由于自身的限制，聚类效果受初始聚类中心的选择与孤立点的影响很大。但是K-means算法初始聚类中心的选取是随机的，这无疑又给最后的聚类效果增加了不确定性。从相关文献中了解到[11-12]，如果考虑数据集中样本点的分布情况，将初始的聚类中心选在数据点分布较密集的地方，聚类的效果会更好。本文的算法在设计时借鉴了密度和最近邻的思想，提出了最近邻点密度的概念，将样本点分为孤立点、低密度点和核心点。首先利用网格化的方法[13]去除孤立点，计算出低密度点和核心点的最近邻点密度，设置阈值，将最近邻点密度小于阈值的低密度点删除。在核心点中选取初始聚类中心，以最近邻点密度最大的点作为第一个初始的聚类中心;按照类间距离最大原则，选取与第一个聚类中心距离最远的点作为第二个聚类中心;然后将与第一和第二个聚类中心距离之和最大的点作为第三个聚类中心，以此方式直到找到所有初始聚类中心。在这个过程中，每选取一个聚类中心，就把该聚类中心所在网格内的所有点删除。最后利用核心点和低密度点进行聚类，聚类完成之后按照距离最近的原则将孤立点分配到相应的类中，完成整个算法。因为基于最近邻的思想对算法做出的改进，因此本文将改进的算法记做Near-K-means算法。

（1）网格化去除孤立点

Step1：根据数据集的分布情況设置坐标轴的刻度，画出数据集的网格散点图，并对散点图上的每个点进行标号;

Step2：记录网格中数据点的数量为1的样本的标号，作为孤立点从数据集中删除;

如图2所示，从图中可以清楚地看到0号，14号和31号所在的网格只有一个样本点，因此这三个点为孤立点，从数据集中找到相应点删除。

（2）最近邻点的查找

Step 1：根据公式（1）计算数据集中所有数据对象之间的两两距离，得到距离矩阵distance;

Step 2：利用公式（4）计算样本中每个样本点的最近邻点个数MinPts，对distance矩阵的第一行进行升序排序，然后从小到大挑选出MinPts+1列，则第二列到MinPts+1列所对应的点即为第一个点的最近邻点;

Step 3：按照Step 2的方式对distance矩阵的其他行进行操作，找到所有点对应的最近邻点。

（3）最近邻点密度的计算

Step 1：利用公式（5）计算出每个点的最近邻点密度dens;

Step 2：依据 dens的值将数据集D={[y1，y2，y3，...，yn]}降序排序，确定最近邻点密度阈值[ρ0]的大小。

（4）查找初始聚类中心，聚类

Step 1：将集合D中dens小于[ρ0]的低密度点删除，更新集合D，然后从集合D中找到dens值最大的点[di]，作为第一个初始的聚类中心;

Step 2：记录点[di]所在网格中所有样本点的标号，从集合D中删除这些点，更新集合D。从distance矩阵中找到点[di]与集合D中其他所有点的欧氏距离，选择与点[di]距离最远的点[dj]作为第二个初始的聚类中心，记录点[dj]所在网格中样本点的标号，从集合D中删除，更新集合D;

Step 3：从distance矩阵中分别找到点[di]，[dj]与集合D中其他样本点的欧氏距离，按照距离之和最大的原则找到点[dl] 作为第三个初始的聚类中心，记录点[dl]所在网格中其他点的标号，从集合D中删除，更新集合D;

Step4：按照Step 3的方式查找，直到找到K个聚类中心为止;

Step5：使用低密度点和核心点的数据，调用K-means算法进行聚类。

（5）孤立点的分配

Step 1：计算每个孤立点与各个聚类中心的距离，把孤立点分配到与其距离最近的聚类中心所属的类中，算法结束。

3 实验及结果分析

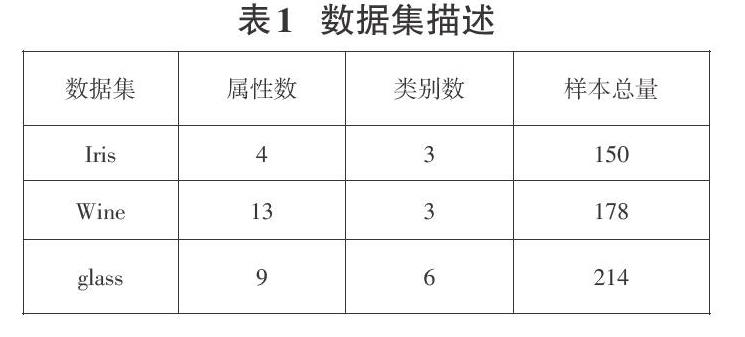
为了验证本文算法的有效性，采用UCI机器学习数据库中的Iris，Wine，glass数据集进行实验。实验环境为：Intel CPU，8GB内存，500 GB硬盘，Windows7 操作系统。编程语言为Python，依据公式（7）将Near-K-means算法与传统的K-means算法的准确率进行对比，除此之外，本文还对迭代次数做了对比。实验所用的数据集描述如表1所示。

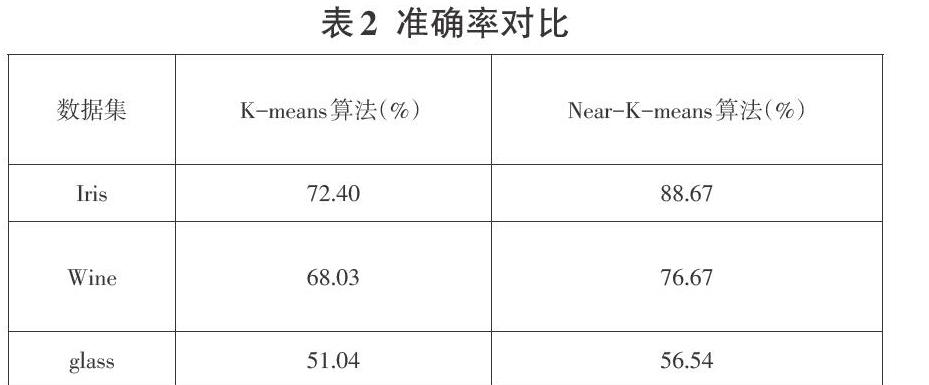
由于传统的K-means算法随机选取聚类中心，因此把传统的K-means算法运行8次，取平均值作为最后的结果。本文改进的K-means算法初始的聚类中心是经过计算选定的，只运行一次作为最后结果。实验结果如表2所示。

由表1的数据描述与表2的准确率对比显示，Iris数据集共有150个样本，含有4个属性，分为3类，运用传统的K-means算法进行聚类时，平均准确率只有72.40%。而运用本文改进的算法进行聚类时，准确率达到了88.67%;Wine数据集有178条数据，每条包含13个属性，运用传统K-means算法与Near-K-means算法分别进行聚类时，准确率分别为68.03%与74.16%，准确率也得到了提高;对于glass数据集，本身分类较多，为6类，一共214条数据。运用传统K-means算法进行迭代时，准确率为51.04%，而运用Near-K-means算法时，准确率提高到了56.54%。

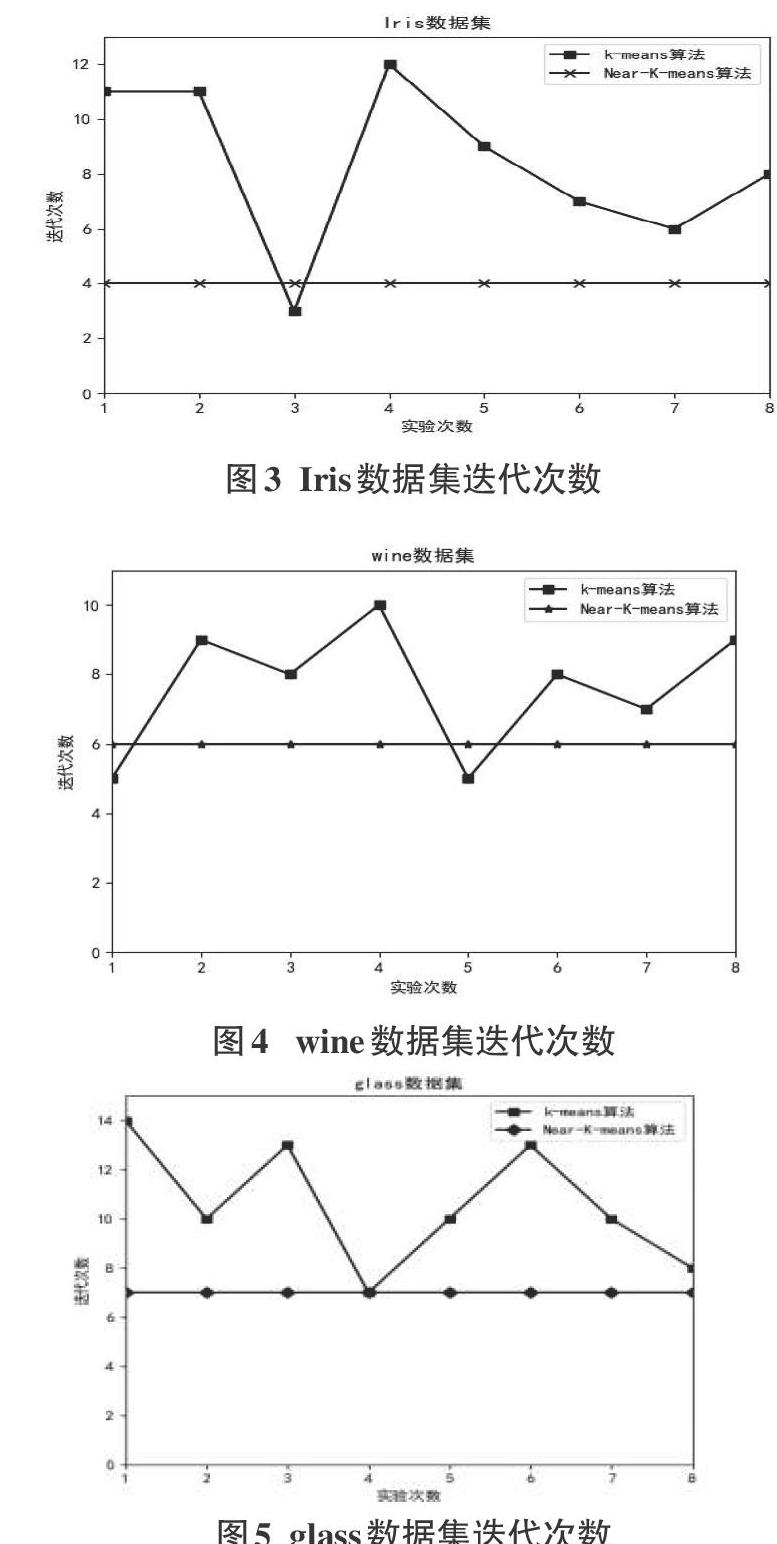
图3、图4、图5的结果显示，在三个数据集上，传统的K-means算法每次实验的迭代次数是不确定的，因为初始聚类中心是随机选取的，这也说明传统的K-means算法不稳定。Near-K-means算法的初始聚类中心是通过更加优化的方式选取的，在三个数据集上的迭代次数更少并且都很稳定，综合表2和图3、图4、图5，与传统的K-means算法相比，本文提出的Near-K-means算法准确率更高，迭代次数更少，更稳定，聚类结果更具有参考价值。

4 结语

本文针对传统的K-means算法聚类效果受初始聚类中心与孤立点影响较大的缺陷，结合密度与最近邻的思想进行改进，提出了一种优化初始聚类中心选择的K-means算法。改进的算法考虑数据集的分布情况，将样本点分为孤立点、低密度点和核心点。在核心点中选取初始聚类中心，并利用类间距离最大原则进行选取，最后根据最小距离原则将孤立点分配到离它最近的聚类中心所属的类中。改善了K-means 算法聚类效果受初始聚类中心与孤立点影响的缺点。经过实验验证 ，本文改良的算法聚类效果更好，准确率更高，更稳定。

但是改进的算法也有不足之处，本文采用网格化的方法删除孤立点时需要设定坐标轴的刻度，在实验中发现，坐标轴刻度的设置直接会影响最后聚类的准确率。如何更加准确的设置坐标轴的刻度，得到更好的聚类效果，将是接下来研究的方向之一。

参考文献：

[1] 李晓瑜，俞丽颖，雷航，等.一种K-means改进算法的并行化实现与应用[J].电子科技大学学报，2017，46（1）：61-68

[2] 高诗莹，周晓锋，李帅.基于密度比例的密度峰值聚类算法[J].计算机工程与用，2017，53（16）：10-17.

[3] 邵伦，周新志，赵成萍，等.基于多維网格空间的改进K-means聚类算法[J].计算机应用，2018，38（10）：2850-2855.

[4] 罗军锋，锁志海.一种基于密度的K-means聚类算法[J].微电子学与计算机，2014，31（10）：28-31.

[5] 冯波，郝文宁，陈刚，等.K-means算法初始聚类中心选择的优化[J].计算机工程与应用，2013，49（14）：182-185+192.

[6] 邢长征，谷浩.基于平均密度优化初始聚类中心的K-means算法[J].计算机工程与应用，2014，50（20）：135-138.

[7] 金晓民，张丽萍.基于最小生成树的多层次k-Means聚类算法及其在数据挖掘中的应用[J].吉林大学学报（理学版），2018，56（5）：1187-1192.

[8] 赵文冲，蔡江辉，赵旭俊，等.一种影响空间下的快速K-means聚类算法[J].小型微型计算机系统，2016，37（9）：2060-2064.

[9] 胡伟.改进的层次K均值聚类算法[J].计算机工程与应用，2013，49（2）：157-159.

[10] 王振武.数据挖掘算法原理与实现[M].北京：清华大学出版社，2016：159-161.

[11] Park H S， Jun C H. A simple and fast algorithm for K-medoids clustering[J].Expert systems with applications，2009，36（2）：3336-3341.

[12] Rodriguez A， Laio A. Clustering by fast search and find of density peaks[J]. Science， 2014，344（6191）：1492-1496.

[13] 何熊熊，管俊轶，叶宣佐，等.一种基于密度和网格的簇心可确定聚类算法[J].控制与决策，2017，32（5）：913-919.

[14] Daszykowski M， Walczak B，Massart D L.Looking for natural patterns in data： Part 1. Density-based approach[J].Chemometrics and Intelligent Laboratory Systems，2001，56（2）： 83-92.

[15] 贾瑞玉，李玉功.类簇数目和初始中心点自确定的K-means算法[J].计算机工程与应用，2018，54（7）：152-158.

【通联编辑：王力】