基于遗传算法的仓内拣货优先问题研究

杨海祥

摘要：网购、快递已经成为这个时代的专有名词。但是在每个快递公司的仓库当中每时每刻都在进行着一场战争——以最快的速度将所有的货物送到买家的手里。该文着重解决遗传算法等思想，给每个拣货员分配任务单、起始拣货复核台，并分别规划理想的拣货路线，使得 49 个任务单尽快完成出库，并计算完成出库需要花费的时间和每个复核台利用率。根据拣货员仓库作业的特点，对目标求解模型进行约束及优化，最后遗传算法为每个工人分配订单后确认其顺序，确定最优的订单分配方案，之后通过排队优化算法解决排队问题。

关键词：遗传算法;排队问题

快递公司的仓库当中每时每刻都在进行着一场战争——以最快的速度将所有的货物送到买家的手里。但是很多的因素会对拣货员的拣货速度造成影响。本文想对当下中国的拣货机制进行一定的改善，其中包括拣货员的路径，拣货员拿货单的顺序，排队最优等部分，将在下面展开讨论。

1 问题分析

首先需要制定距离的计算公式，在行走速度相同的情况下，距离越短，时间越短。货格与货格、货格与复核台、复核台与复核台之间均分别存在着特殊的位置关系，观察分析后，为方便对模型进行描述和求解，我们根据仓库示意图对仓库内的元素用三维数组进行编号，将3013个元素分为货格与货格、货格与复核台、复核台与复核台三种情况分别进行计算，再分别建立模型并求解结果。

然后将问题简化为起点固定、有13个终点可以选择的路径优化问题，运用启发式算法、遗传算法等思想，最短距离求解模型建立一个有起点、有终点、有活动的最短路径目标求解模型，根据拣货员仓库作业的特点，对目标求解模型进行约束及优化，再对模型进行编程求解。

利用上面的模型将每个任务单完成需要的时间确定出来，之后通过时间升序排序，可以极大节约订单等待时间。49个任务单从开始的那一刻将有9个任务单同时分配给9个拣货员，之后9个拣货员完成所规定的任务单时间能够确定，但是由于复核时间为30秒，复刻台只有4个，肯定存在等待时间，所以可以等待问题简化为经典的排队问题，每当一个任务单复核完成我们将给他在此复核台直接分配下一个任务单，直至所有任务单完成。即为拣货员的最佳完成时间。

2 模型的建立与求解

现根据仓库货格的编号[abc]，首先建立距离计算模型。

假设任意两个货格的编号为[aibici]，[ajbjcj]。当两个货格在同排同一巷道内且同一侧时，这两个货格之间的距离即为纵向距离加一个巷道的宽度1500毫米，则距离[dij]为：

当两个货格在不同的巷道内，无论在同一侧还是不同侧时，都需要首先判断拣货员从巷道和通道交叉的哪个方向出来，因此，需要先进行最小路径的优先选择。按从下至上的顺序第一排内两货格的距离计算[dij]为：

综上，将任意两货格之间距离的计算分为四种情况，对于货格不同的位置情况，对应不同的公式，利用上述模型求出距离后，结合每个货格的长和宽，即可求出任意两货格之间的距离。货格与复刻台以及复刻台与复刻台之间的计算在此省略。

同时将整个拣货路径优化模型定义为：

综上，将任务单[T0001]内的每个货格以及起点复核台[FH10]、[13]个可以作为终点的复核台代入，求解得最优路径。

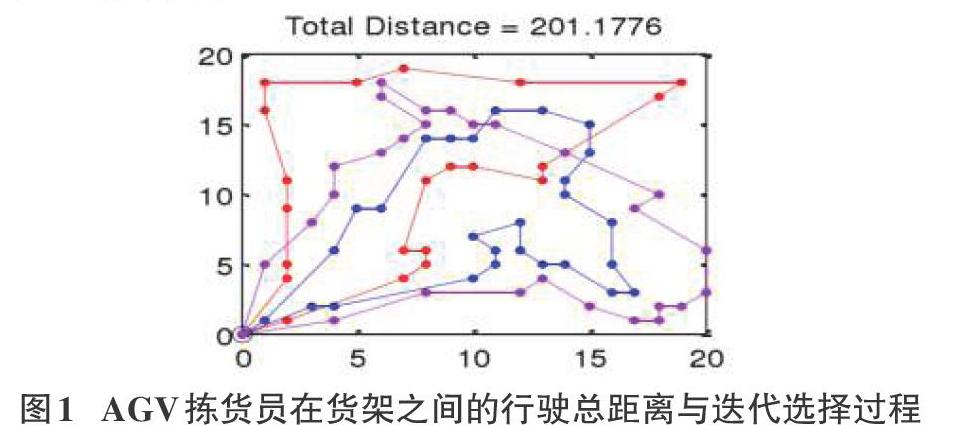
将上述模型中的拣货员分批后的每一批订单所在的货架位置信息输入到系统中来，应用matlab 来对遗传算法进行实现，通过求解得出每一台AGV拣货员的任务分配及路径优化结果。对订单按照货架信息进行任务分配及路径规划。

批订单中包含49个订单，其共分布在不同的货架上，各个货架的货格坐标由第一问的模型已知其三维坐标位置。

此处的坐标如（5，1，6） 代表货架所在的位置信息为所有货架的第一巷道右侧第六个货格。将以上的货架货格位置信息导入到算法中。

由运行结果可知，当算法迭代到48465次的时候得到最优解，此时最短路径为367.5，并且可通过运行得出下表每个AGV拣货员搬运的距离。

3 结论

在仓库货格与货格之间、货格与复核台之间以及复核台与复核台之间计算距离的数学模型，是将问题简化后所建立的，可描述性强。对于完成任务单最短路径计算的模型，运用了最短路径的求解思想，使得模型转化为原点、活动以及终点之间的最短距离求解问题，降低问题复杂性，使得数学模型更易懂。

在拣货最优的遗传算法中，可以不受函数约束条件的限制，直接通过设定初始的值，满足不同的需求，得出不同的最优解。具有全局搜索性，遗传算法的搜索过程是从全局开始，在此过程中全局最优解可得，而不会落入局部最优的循环不能得到结果。综上所述遗传算法非常适合解决拣货最优的问题。

参考文献：

[1] 陈文.仓储物流机器人批量拣选路径规划仿真[J].安阳师范学院学报，2019（5）：35-39.

[2] 张新艳，周雨晴.基于魚骨型仓库的拣选路径问题优化[J].同济大学学报（自然科学版），2019，47（11）：1683-1690.

[3] 冯爱兰，张小青，孔继利.基于聚类和动态规划的组合路径策略[J].运筹与管理，2019，28（8）：86-92.

[4] 刘建胜，雷兆发，聂伟豪，等.一种fishbone仓储布局下的拣选路径优化方法研究[J/OL].中国机械工程：1-8[2020-05-24].http：//kns.cnki.net/kcms/detail/42.1294.TH.20190717.1543.002.html.

[5] 罗志文.基于改进鱼骨型仓储布局多人协同拣货路径优化方法研究[D].南昌大学，2019.

[6] 盛虎宜，刘长石，鲁若愚.基于共同配送策略的农村电商集送货一体化车辆路径问题[J].系统工程，2019，37（3）：98-104.

[7] 于浩洋.基于遗传算法的拣货路径优化方法[J].中国科技信息，2019（8）：91-94.

[8] 王晟旭，皇甫遥遥.基于猫群算法的人工拣选作业路径优化研究[J].中国储运，2020（3）：116-119.

[9] 邵刘霞，张瑞.配送中心拣选作业理论研究[J].中国市场，2012（28）：11-12，16.

[10] 李诗珍.配送中心拣货作业优化设计与控制研究[D].西南交通大学，2008.

[11] 白寅.基于偏离度的仓库拣货路径优化方法及应用[D].华中科技大学，2012.

[12] 刘思佳.A公司仓储中心出库作业优化研究[D].吉林大学，2014.

[13] 薛永吉.仓储物流系统仿真及应用研究[D].东南大学，2006.

[14] 张彩霞.基于“货到人”模式的电商订单拣选优化研究[D].浙江理工大学，2016.

【通联编辑：代影】