基于Lyapunov稳定性理论的移动机器人轨迹跟踪控制
2021-04-13张明扬郭海峰
张明扬 郭海峰

摘要:针对非完整轮式移动机器人的高度强耦合、欠驱动非线性动力学模型,设计了运动学控制器以及动力学力矩控制器,使得移动机器人轨迹能够跟踪理想轨迹。这种方法的实质是首先设计虚拟速度控制器,输出速度的期望值,然后设计基于模型的力矩控制器。最后通过simulink软件对所设计的系统进行仿真,结果表明对于非完整机器人的轨迹跟踪这种控制方法效果较好。
关键词:非完整移动机器人;虚拟速度控制器;轨迹跟踪
Abstract: In view of the nonholonomic wheeled mobile robots high-intensity coupling and underdrive nonlinear dynamic model, the speed controller and dynamic torque controller are designed, to optimize trajectory tracking. The nature of this method is to design the virtual speed controller first, output the expected speed and then design the model-based torque controller. Lastly, simulation conducted through simulink shows that this control method delivers a better result for nonholonomic robots.
Key words: nonholonomic mobile robot; virtual speed controller; trajectory tracking
非完整輪式机器人在国防和民用领域都有着广泛应用。目前在轮式机器人轨迹跟踪研究中,通常假设轮子与地面的摩擦力起关键作用,而轮子在地面上不产生滑动是一种纯滚动,这种理想化假设使得这一问题成为典型的多输出非完整约束的动力学系统。考虑在工程实践中存在大量的不确定因素影响轨迹跟踪性能,例如非完整轮式机器人的负载变化以及惯量参数的摄动、部件之间的磨损误差以及外部干扰等。这些不确定因素增加了非完整轮式机器人部件之间运动的耦合性和时变性,使得这一非线性机器人的轨迹跟踪控制更加复杂、难度更大。迄今为止没有找到一种通用的控制器 [1-10]。
目前这一领域已经报道的研究文献主要集中在PID控制[1-2]以及模糊控制理论[1,3]、神经网络[3]、模型预测控制[4-6]、变结构控制[7-8]、鲁棒控制[9-11]等现代控制方法,但各种方法都局限于单一运动学控制器或单一动力学控制器的研究。
有鉴于此,本文采用的双回路的控制策略对此进行改进,针对非完整轮式移动机器人的非线性动力学模型,设计运动学控制器以及动力学力矩控制器。本文的主要工作:1)首先,建立非完整轮式移动机器人的动力学模型,这和大多数研究一样是根据Euler-Lagrange方程;2)其次,根据Lyapunov函数设计虚拟速度控制器,为动力学模型提供跟踪速度信息;3)再次,根据基于模型控制的方法设计动力学控制器,即自适应控制力矩,用来跟踪有虚拟速度控制器输出的速度和角速度,根据系统的速度信息计算出位置;4)最后,采用simulink软件对所设计的系统进行仿真。
1 非完整三轮轮式移动机器人模型
如图1所示,一个安装有三个轮子的非完整轮式机器人,后面的两个差速驱动轮负责动力驱动和方向控制,安装在前面的随动轮负责姿态调整、防止翻车;后面安装在同一个轴上的两个驱动轮,分别由两个直流电机驱动,控制直行或者转弯。机器人关注点F的广义位置坐标[q=[x,y,θ]T],两个驱动轮有相同的半径r,轮距为2L,轴线的重点为G,力矩分别为[τl],[τr];G的坐标为(xG,yG),F的坐标为(xF,yF),G与F的距离为d。
1.1非完整三轮轮式机器人的运动学模型
有上述分析可知,这个机器人关注点F和机器人驱动轮轴线重点G之间的位置坐标为:
2 机器人控制器的设计
首先根据期望轨迹得到期望速度,再由Lyapunov稳定理论方法设计虚拟速度控制器;它为力矩控制器提供速度信息,在通过力矩控制器对动力学模型进行控制,得到系统输出的速度信息,根据速度信息得到相应的位置信息。系统的控制框图如图2所示。
2.1 机器人虚拟速度控制器的设计
3仿真
本文采用的Matlab 2016b 中Simulink软件,在十代i5、16G内存的电脑上,对所设计的系统进行仿真。功能强大的Simulink软件为用户提供S-function函数以便用户自定义模块,通过模型建立和系统设计,我们设计了参考轨迹、控制器和被控对象三大模块。选择参考轨迹如下描述为:
如图2所示,通过系统的虚拟速度控制器输出速度的控制信息,并将信息传递给力矩控制器;再通过力矩控制器使得被控对象输出的实际速度与期望速度满足如下关系:
再应用实际速度计算出移动机器人具体位置信息和轨迹,控制减少误差量能够跟踪期望轨迹。非完整三轮轮式移动机器人的质量、车轮半径、宽度、惯量、关键点之间的距离等主要参数如表1所示。
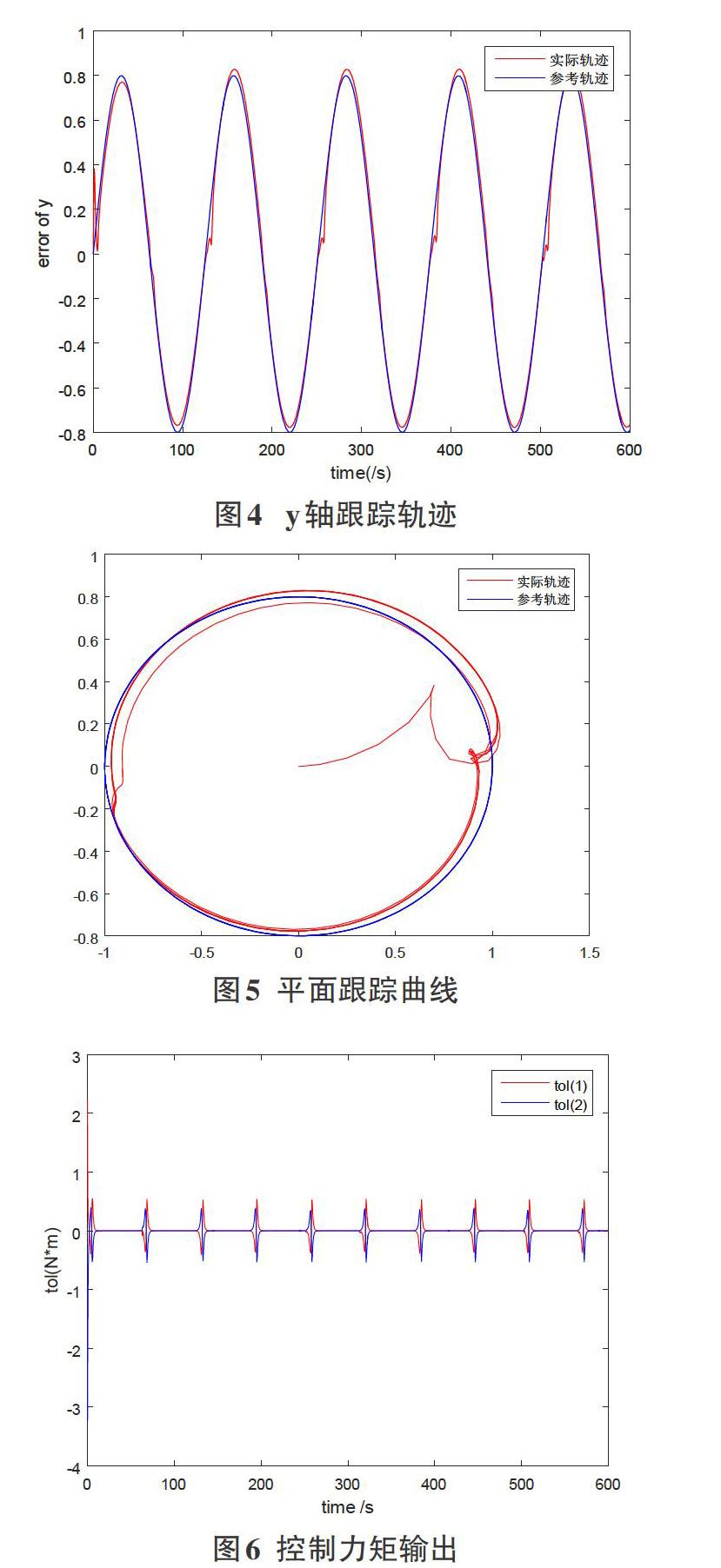
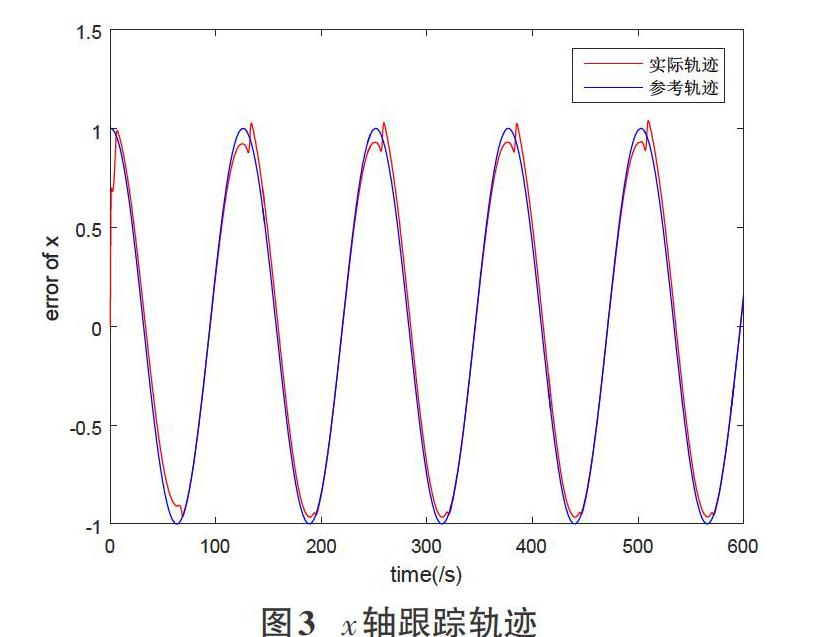
如图3、图4表明,机器人在x轴和y轴的期望轨迹与参考轨迹基本重合;图5中红线为实际运动轨迹、蓝线是参考轨迹,由图可知参考轨迹与实际随着时间逐渐重合,这表明机器人的全局跟踪轨迹效果良好;图6为机器人控制输出力矩,结果表明本文设计的控制器对于移动机器人的关注点对于参考轨迹有较好的轨迹跟踪性能。
4结论
針对具有不确定约束的非完整轮式移动机器人的轨迹跟踪问题,为改进现有研究文献中要么研究运动学控制器的设计策略,要么研究或动力学控制器的设计策略,这种局限于单一控制器设计策略的研究现状,本文将非完整轮式机器人在大量不确定环境下控制虚拟速度的设计策略和基于模型预测控制的方法相结合,设计双回路控制器:采用自适应控制理论设计虚拟速度控制器,为机器人提供需要的控制速度数据;再利用基于模型控制的方法设计力矩控制器,使得机器人能够跟踪虚拟速度控制器提供的速度信息,可以通过相应的计算得到位置信息。最后,通过仿真Simulink软件仿真来验证了这一控制方案的有效性和鲁棒性。
进一步的研究,可以考虑更接近实际工程环境的控制策略,在三维立体空间、多斜坡复杂路面的多种不确定情况下研究这种控制策略的有效性和改进方案。
参考文献:
[1] 刘国荣,张扬名.移动机器人轨迹跟踪的模糊PID-P型迭代学习控制[J].电子学报,2013,41(8):1536-1541.
[2] 冯剑,张文安,倪洪杰,等.轮式移动机器人轨迹跟踪的PID控制方法[J].信息与控制,2017,46(4):385-393.
[3] 高兴泉,陈虹.基于T-S模型的轮式移动机器人轨迹跟踪控制[J].控制理论与应用,2007(6):873-878.
[4] 王昕.基于模型预测控制的移动机器人轨迹跟踪[J].电脑知识与技术,2009,5(27):7738-7740.
[5] 曾志文,卢惠民,张辉,等.基于模型预测控制的移动机器人轨迹跟踪[J].控制工程,2011,18(S1):80-85.
[6] 吴菁,陈罡,孟静.基于预测控制的非连续路段下移动机器人的轨迹跟踪[J].计算机测量与控制,2016,24(10):74-78.
[7] 张鑫,刘凤娟,闫茂德.基于动力学模型的轮式移动机器人自适应滑模轨迹跟踪控制[J].机械科学与技术,2012,31(1):107-112.
[8] 张扬名,刘国荣,杨小亮.基于滑模变结构的移动机器人轨迹跟踪控制[J].计算机工程,2013,39(5):160-164.
[9] Huang D, Zhai J, Ai W, et al. Disturbance observer-based robust control for trajectory tracking of wheeled mobile robots[J]. Neurocomputing, 2016, 198(C):74-79.
[10] 陈罡,高婷婷,贾庆伟,等.带有未知参数和有界干扰的移动机器人轨迹跟踪控制[J].控制理论与应用,2015,32(4):491-496.
[11] 邹左明,刘丛志.基于H∞滑模控制的移动机器人轨迹跟踪研究[J].机床与液压,2017,45(11):28-31,174.
[12] Papadopoulos E, Poulakakis J. Planning and model-based control for mobile manipulators[C].International Conference on Intelligent Robots and Systems. IEEE, 2000,3:1810-1815.
【通联编辑:梁书】
