混合式配电变压器的动态模型与内环控制系统

柳轶彬 梁得亮 王宇珩 高亚晨 张立石

混合式配电变压器的动态模型与内环控制系统

柳轶彬1,2梁得亮1,2王宇珩1,2高亚晨1,2张立石1,2

（1. 电力设备与电气绝缘国家重点实验室（西安交通大学电气工程学院） 西安 710049 2. 陕西省智能电网重点实验室 西安 710049）

相比传统配电变压器，混合式配电变压器（HDT）集成了脉冲宽度调制变换器，能够对部分传输功率进行调控。因而不仅具有传统配电变压器电压等级变换和电能传输的基本功能，而且能够实时动态控制其负载电压及电网电流，这对于实现主动配电网具有重要应用价值。该文提出一种改进型混合式配电变压器配置方案及其三相电路拓扑，其优势在于变换器拓扑简单，各环节电压等级的确定灵活方便。基于等效电路构建HDT的传递函数框图模型，并采用PI控制器构建HDT的内环控制系统。仿真及实验显示，在电网电压波动及负载畸变工况下，HDT能够实现电网电流的正弦单位功率因数控制及负载电压的正弦稳定控制，从而验证了建模分析及控制系统设计的正确性。

主动配电网 等效电路 混合式配电变压器 PI控制 传递函数

0 引言

混合式配电变压器（Hybrid Distribution Transformer,HDT）是对传统配电变压器进行改进设计，并将脉冲宽度调制（Pulse Width Modulation, PWM）变换器接入其中的一类新型配电变压器[1-4]。借助PWM变换器灵活的控制功能可以使配电变压器不再仅限于电压等级变换与电能传输。具体而言，通过PWM变换器对配电变压器的部分传输功率进行调控，HDT能够对电网电流及负载电压进行实时控制，这对于构建未来主动配电网[5-10]具有重要意义。

由于PWM变换器及变压器的电路拓扑和联结方式种类有很多，因而HDT的种类也很丰富。文献[11-13]采用AC-AC变换器提出无直流环节HDT，并对其基本原理、建模分析和功能验证进行了详细说明。此类HDT的主要优点在于无需使用直流母线电容，系统结构简单，成本低，经济性好。但此类HDT没有电流补偿能力，其功能主要在于电压幅值的调节，而对于电压相位控制则明显不足。此外，相比具备直流环节的电压源型变换器，AC-AC变换器难以通过续流二极管进行自然换流，因而往往还需要附加一些比较复杂的辅助设备实现可靠换流，这会使HDT系统整体更为复杂，成本更高，进而使得此类HDT大规模推广应用比较困难。

为此，文献[14-18]提出了采用AC-DC-AC变换器的HDT方案，并指出AC-DC-AC型HDT功能强大，能方便实现电网电流及负载电压的实时调控，是构建未来智能配电网的可选方案。文献[14]给出了采用AC-DC-AC型变换器构建的多种HDT配置方案，并给出了HDT样机运行效果。文献[15]对于HDT相比传统配电变压器及电力电子变压器的优点进行定性比较分析，并对于HDT的保护方案进行讨论说明。文献[16]对配电变压器未来的发展趋势进行了定性分析，并指出HDT用于近期智能配电网的巨大优势，但未对HDT的模型及控制策略进行说明。文献[17-18]针对一种将变换器配置在低压侧的HDT进行研究，采用PI控制器分别对负载电压及电网侧功率因数进行控制，并仿真验证了控制系统设计的有效性，但文中的HDT配置方案将变换器置于低压侧，导致主变压器设计时不得不考虑电网电压的波动。文献[19]提出一种三相HDT拓扑，并给出系统模型及其复合控制框图。但所设计的三相电路拓扑在网侧采用星形中性线引出接法，这其实并不完全符合实际配电网的应用需求。

现有报道虽然给出了多种基于AC-DC-AC变换器的HDT的配置方案，并初步实现了相应的控制功能。但总体来讲，目前的方案存在以下缺陷：

（1）HDT的配置方案往往不含隔离变压器，这导致三相场合的HDT中用于负载电压补偿的变换器往往需要采用三个单相全桥变换器，这显然会大大增加HDT变换器的复杂程度，并导致控制复杂，系统可靠性降低。此外，因为没有隔离变压器，HDT的AC-DC-AC变换器公共直流母线的额定电压完全由所在配电网场景的补偿深度决定，此时变换器功率器件的选型范围往往很窄。具体来讲，如果电压控制变换器位于配电网高压侧，必然导致变换器直流母线额定电压很高。而如果电压控制变换器位于配电网低压侧，直流母线额定电压很低，从而使得电流控制变换器的电流很大。这导致一大部分技术成熟、性价比很高的功率器件因电压或电流等级不符合现场要求而无法被采用，此时不仅器件选型困难，而且HDT系统整体的经济性及可靠性均很低。

（2）将用于控制负载电压的变换器单元配置在配电网低压侧不利于充分发挥HDT的控制功能。由于配电网的电压波动主要发生在高压侧，进而导致二次侧负载电压发生波动，若将变换器单元整体布置于配电网低压侧，只能抑制配电网电压负载侧的电压波动，而无法抑制HDT一次绕组及控制绕组电压的波动。此时，在设计HDT的变压器本体时，必需增大铁心面积以避免电网电压变高而导致的铁心饱和。而且当电网电压突变时，控制绕组也会发生电压突变，这必然会影响HDT对电网电流的补偿效果。

（3）能应用于实际配电网场景的三相HDT电路拓扑研究较少，十分不利于HDT的产业化推广。

（4）对于HDT的原理分析及控制系统设计，缺乏比较直观准确的动态模型，这导致目前关于HDT工作原理的分析大多局限于定性说明，给HDT控制系统的设计带来不便。

本文基于在传统配电变压器中增设第三控制绕组的报道[14]，设置隔离变压器于配电网高压侧，将其高压侧与三绕组配电变压器高压侧串联，然后通过控制绕组及隔离变压器低压绕组将电容中点引出式背靠背半桥PWM变换器接入配电变压器，从而给出一种新型HDT实用配置方案。基于这一配置方案，提出一种实用的三相HDT拓扑，该拓扑在高压侧采用三角形联结，而其余绕组均采用中性线引出的星形联结。根据HDT的单相等效电路，建立HDT的微分方程，并导出系统的传递函数框图，基于框图模型，指出HDT能够控制电网电流及负载电压的根本原因，进而采用PI控制器设计HDT的内环控制系统。在电网电压波动及负载畸变工况下进行仿真及样机实验，验证本文提出的HDT电路拓扑及所设计的内环控制系统的正确性。

1 HDT的配置方案与三相电路拓扑

本文提出的HDT配置方案如图1所示。

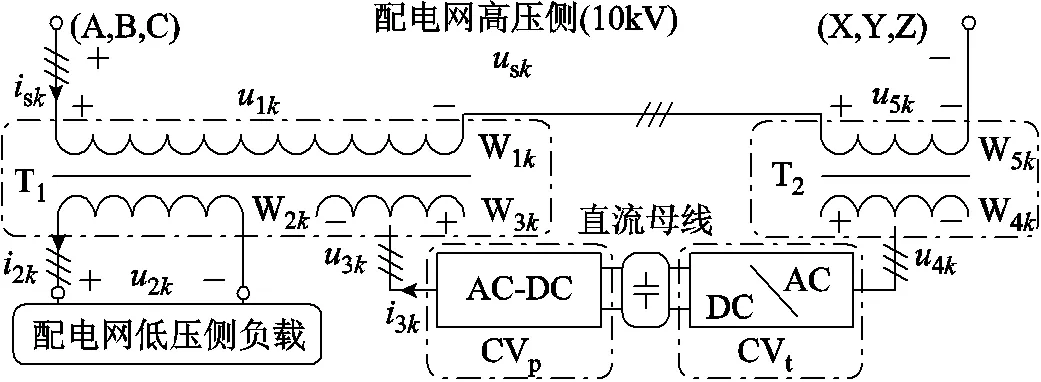
图1 HDT的配置方案

在图1中，T1是HDT的主变压器，共包含三个绕组（W1k，W2k，W3k，为三相的相序号，=a,b,c）。T1相当于在传统双绕组配电变压器的基础上增设控制绕组W3k。T2是双绕组的隔离变压器(W4k，W5k)。CVp和CVt是共用直流母线的两个电压源型PWM变换器，二者分别与W3k和W4k相连。W1k与W5k串联为一个整体后接入配电网10kV高压侧。W2k为配电网低压侧负载供电。1k~5k为绕组W1k~W5k的绕组电压。

当CVp和CVt退出时，HDT就相当于传统配电变压器。而当CVp和CVt投入运行后，就可以对HDT的电网电流及负载电压进行调控。具体来讲，CVp可被控制成一个可控电流源，即图1中的3k实时可控。借助变压器的磁动势平衡原理，在T1中，当负载电流2k出现谐波、无功、不对称分量时，3k便会产生相应的反向补偿分量，从而使电网电流sk始终被控制为对称的正弦波，而且网侧始终接近单位功率因数。CVt可被控制成一个可控电压源，而通过T2则能将CVt产生的补偿电压进一步升高。在图1中，当电网电压sk出现波动和不对称等工况时，CVt便可以实时控制T2高压绕组W5k的电压5k，进而实时抵消sk中的波动和不对称分量，从而使T1各绕组电压及负载电压2k稳定在额定值附近。

配电网为三相应用场合，因而给出一种合理的三相电路拓扑更具实用价值。图2所示为本文基于图1所示HDT的配置方案提出的一种高压侧采用三角形联结的HDT三相电路拓扑。

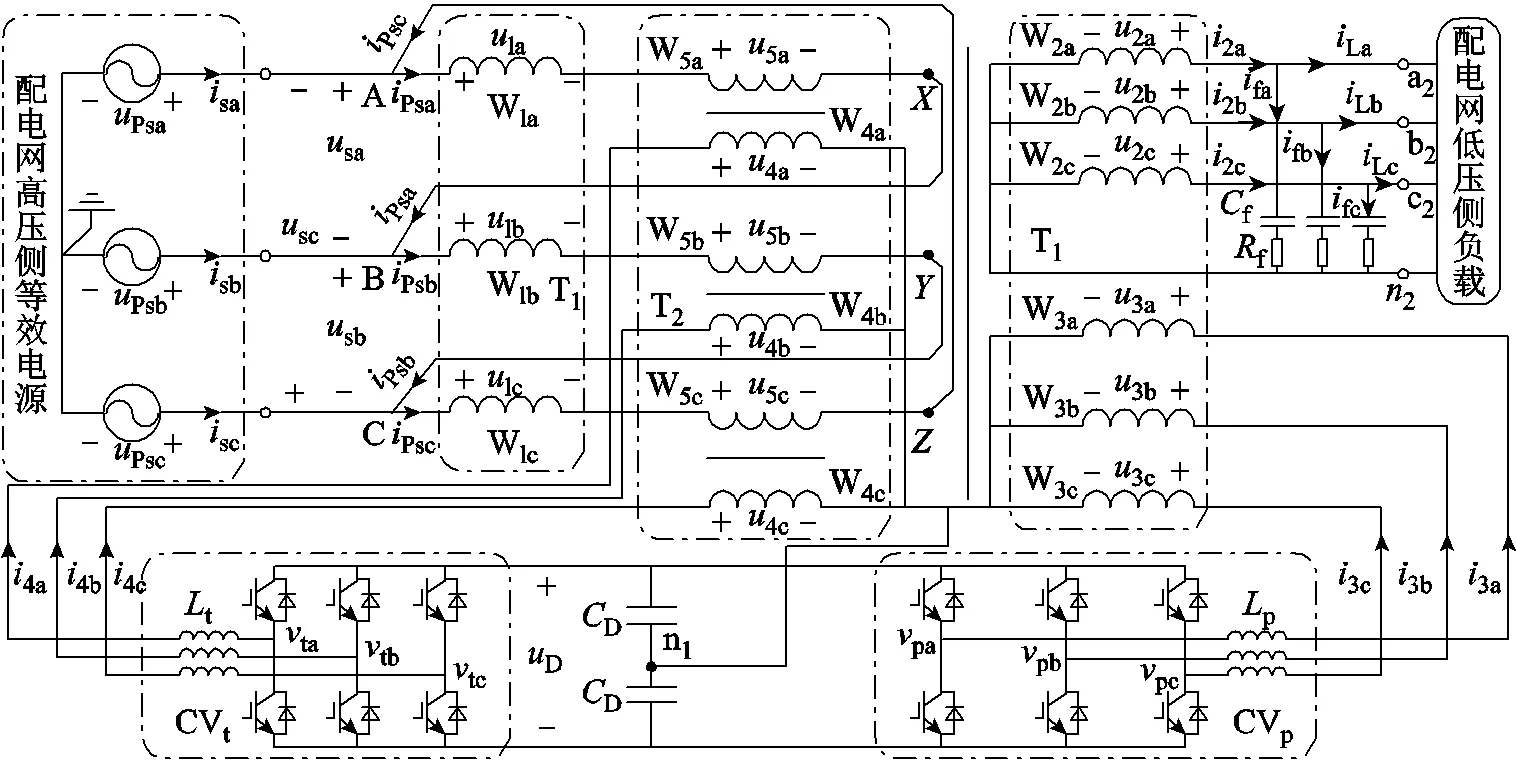
图2 HDT的三相电路拓扑

与图1对应，图2中的1k~5k为绕组W1k~W5k的绕组电压。Psk为W1k与W5k的绕组电流，而2k、3k及4k分别为W2k、W3k、W4k绕组电流。f与f构成RC滤波器。Lk为负载电流，fk为RC滤波支路的电流。

如图2所示，本文提出的HDT三相电路拓扑将W1k与W5k构成的整体采用三角形联结接入配电网高压侧。而W2k、W3k、W4k均采用星形中性线引出联结。此外，CVt与CVp共用直流母线构成背靠背PWM变换器，其直流母线采用分裂电容中点引出式结构，电容中点n1引出后与W3k和W4k的中性线连在一起，构成变换器零序通路，便于实现零序补偿。tk、pk分别为CVt与CVp的桥臂中相对于n1的电压。p、t为CVp和CVt的输出连接电感。连同t及p一起能抑制变换器产生的高次谐波对于负载电压及电网电流的影响。

图2所示方案具备以下优势：

（1）高压侧采用三角形联结接入配电网高压侧，不仅能隔离配电网高压侧电源电压Psk中的零序分量对HDT的影响，而且能阻断HDT高压侧绕组W1k与W5k的电流Psk中的零序分量注入电网。

（2）配置隔离变压器T2于配电网的高压侧，将CVt通过T2接入配电网，并利用CVt直接对高压侧电网电压的波动进行抑制。这样，一方面，CVt能够避免使用无隔离变压器时比较复杂的三个单相全桥结构；另一方面，CVt直接在高压侧抑制电压的波动，从而在设计T1时无需再额外增加铁心截面来防止高压侧电网电压波动引发的磁饱和。

（3）T2的电压比及T1中W3k与W1k的电压比均灵活可调，于是CVt及CVp直流母线的额定电压也能灵活确定。这样，将能选用目前最常用电压等级及电流等级的功率器件来搭建CVt及CVp的主电路，方便了HDT的设计制造。

（4）采用的PWM变换器仅由六个半桥构成，相比其他变换器拓扑，本文采用的配置方案不仅结构简单，控制容易，而且兼备零序补偿，功能全面。

2 等效电路与系统微分方程

为方便建立图2所示HDT的数学模型，建立如图3所示的HDT单相等效电路。

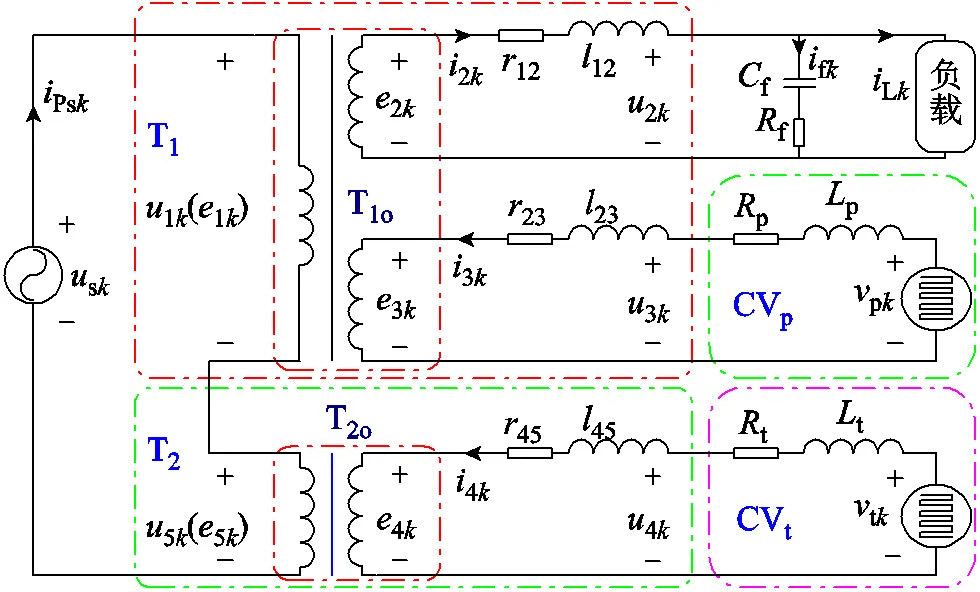
图3 HDT的单相等效电路

图3中，各电压电流与图2含义一致。T1o和T2o是理想变压器，1k~5k是W1k~W5k的绕组电动势。忽略励磁电流，T1可用T1o、电阻12、23及漏感12、23等效；而T2可用T2o、电阻45及漏感45等效；p和t为功率开关的等效电阻。

根据图3所示等效电路，可分别针对CVp及CVt所在回路构建各元件的微分方程。

首先对于CVp的p及23所在支路，有

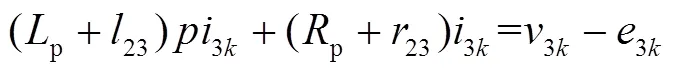
式中，为微分算子。

在T1中，根据磁动势平衡原理可得

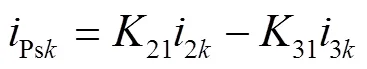
根据电压比关系可得

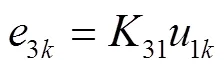
式中，K为绕组W和W的匝数比，、为绕组序号，可取1、2、3、4、5。

由式（1）可知，通过控制CVp的桥臂输出电压pk，便完全能够实时控制W3k的电流3k。如果2k中含有谐波、无功和不对称等分量，则只需控制pk使3k包含极性相反的电流分量来抵消2k中的谐波、无功和不对称等分量，便能使Psk成为对称的正弦波，而且功率因数为1。相应的电网线电流sk也必然呈现对称的正弦波。

显然在式（1）和式（2）中，通过pk实现Psk单位功率因数正弦对称控制，主要任务是克服2k和3k对系统造成的影响，其中，3k与1k呈线性关系。如果1k能被控制为近似不变，则来自3k的扰动将对Psk影响很小。

而对于CVt的t及45所在回路，显然有

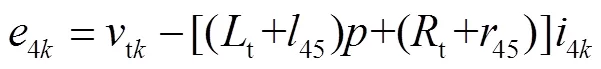
在T2中，根据电压比关系

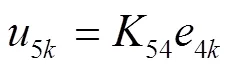
在高压侧所在回路

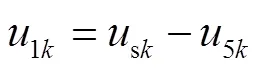
在T1中，根据电压比关系

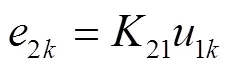
在T1、T2中根据磁动势平衡原理

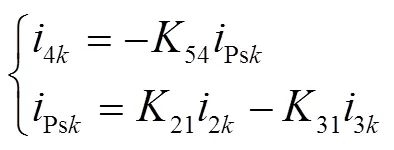
在W2k所在回路

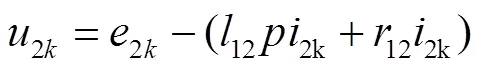
而在RC滤波支路

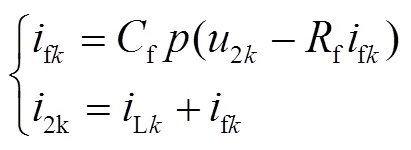
由式（4）~式（7）可知，当电网电压sk发生波动时，通过控制tk，便能实时控制T2的电压5k等于sk中的波动部分，从而抵消电网电压的波动，使1k近似稳定在额定值附近，从而使2k也近似稳定在额定值附近。2k与2k只相差了短路阻抗（12、12）上的压降，因而2k也能近似稳定。式（4）、式（8）~式（10）整体其实构成了一个RLC低通滤波器，能够减少2k中的高次谐波，这体现在后文化简后的传递函数框图中。

式（4）~式（10）揭示了通过tk实现2k实时控制的可行性，其中，sk是系统中的最主要扰动，而Psk及2k会在连接电感t、45、12上产生压降，从而对2k产生影响，但相比sk，其幅值很小。因而在HDT中通过CVt控制2k主要需要克服来自sk的扰动影响。

本文采用SPWM对CVp及CVt进行调制，调制时采用不对称规则采样法。设采样周期为s，则s=0.5w，w为开关周期。本文仿真及实验均采用10kHz的开关频率，则w=0.1ms，s=50ms。

综合考虑调制、采样、控制芯片计算的时间延迟，本文将CVp和CVt均近似等效为一个小惯性环节。具体如下：设pk及tk分别为CVp和CVt的输入调制信号，则在域中，pk()与pk()、tk()与tk()之间满足

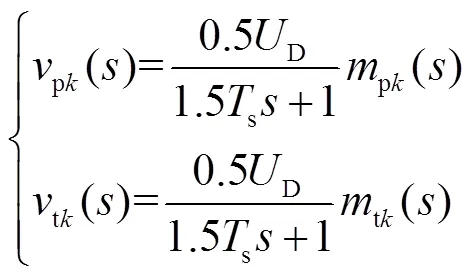
式中，D为D的额定值。

式（1）~式（10）描述的是HDT在静止坐标系下的数学模型，对于揭示HDT的基本工作原理，说明其可行性具有重要意义。但是通常情况下，HDT往往需要实现单位功率因数控制，因而在同步旋转坐标下设计控制器更为方便。

为此本文采用坐标变换，坐标变换矩阵采用等长变换矩阵，以W4k的绕组电压4k为例。

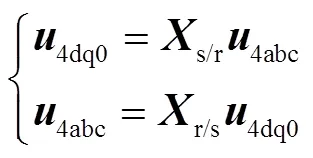
式中，4abc=[4a4b4c]T；4dq0=[4d4q40]T。本文中其他三相电压电流的变换关系与4k一致。

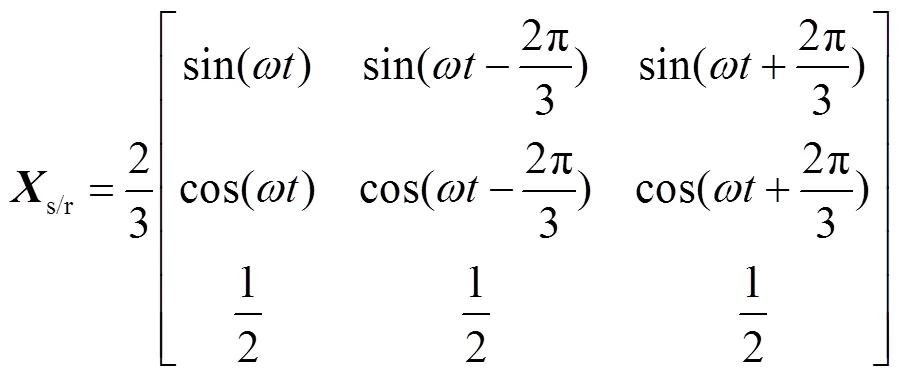
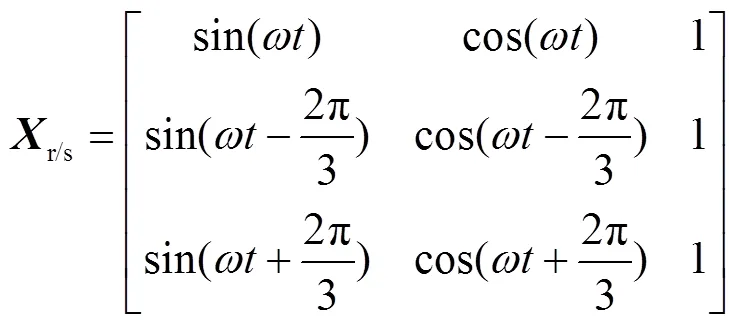
式中，=2π0，0为电网频率。

对式（1）~式（3）进行坐标变换，可导出CVp所在回路在同步旋转坐标下的数学模型，在域表示为

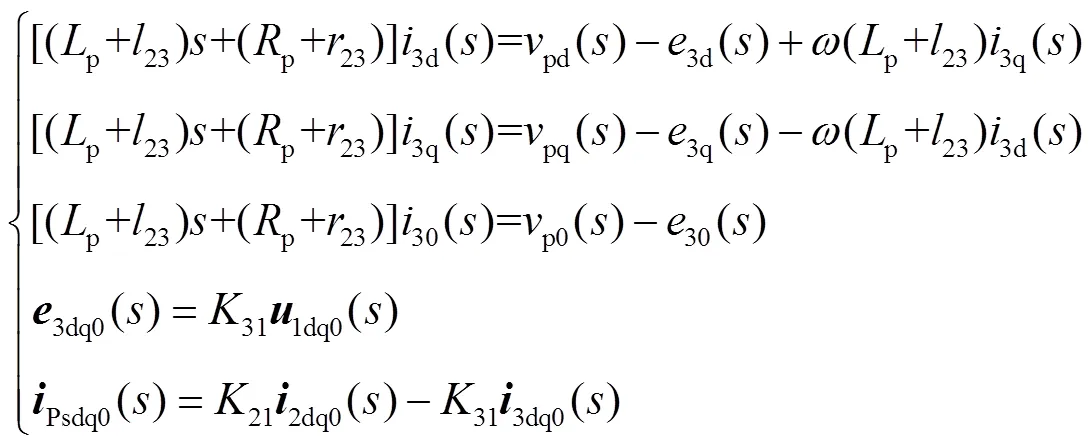
同样对式（4）~式（10）进行坐标变换，也在域表示，可得CVt所在回路在同步旋转坐标下的数学模型为

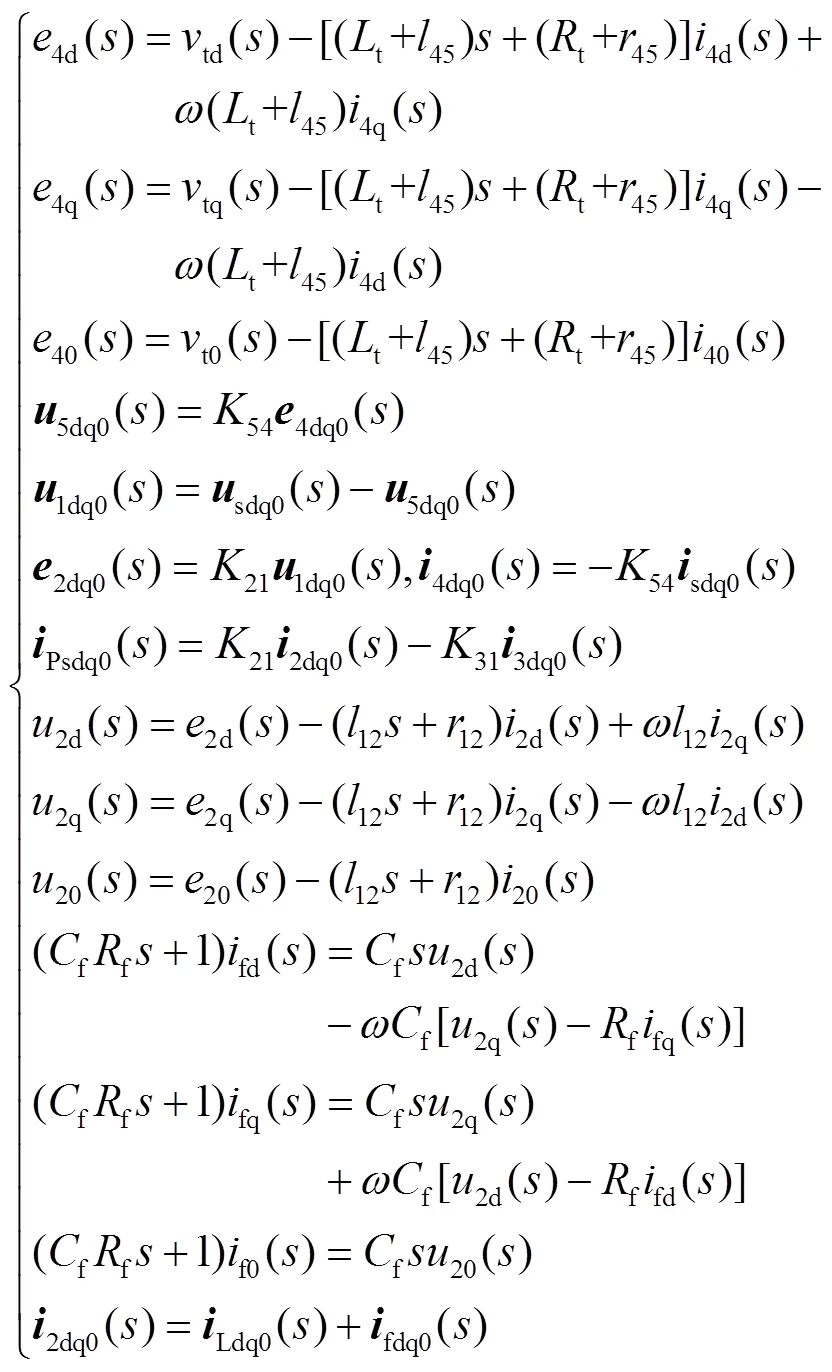
对式（11）进行近似处理。在同步旋转坐标中

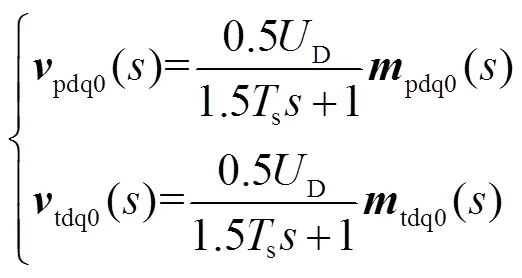
3 传递函数模型及控制系统

根据式（15）可给出同步旋转坐标系下，从pdq0()到Psdq0()模型框图，如图4中点画线框内部分所示。

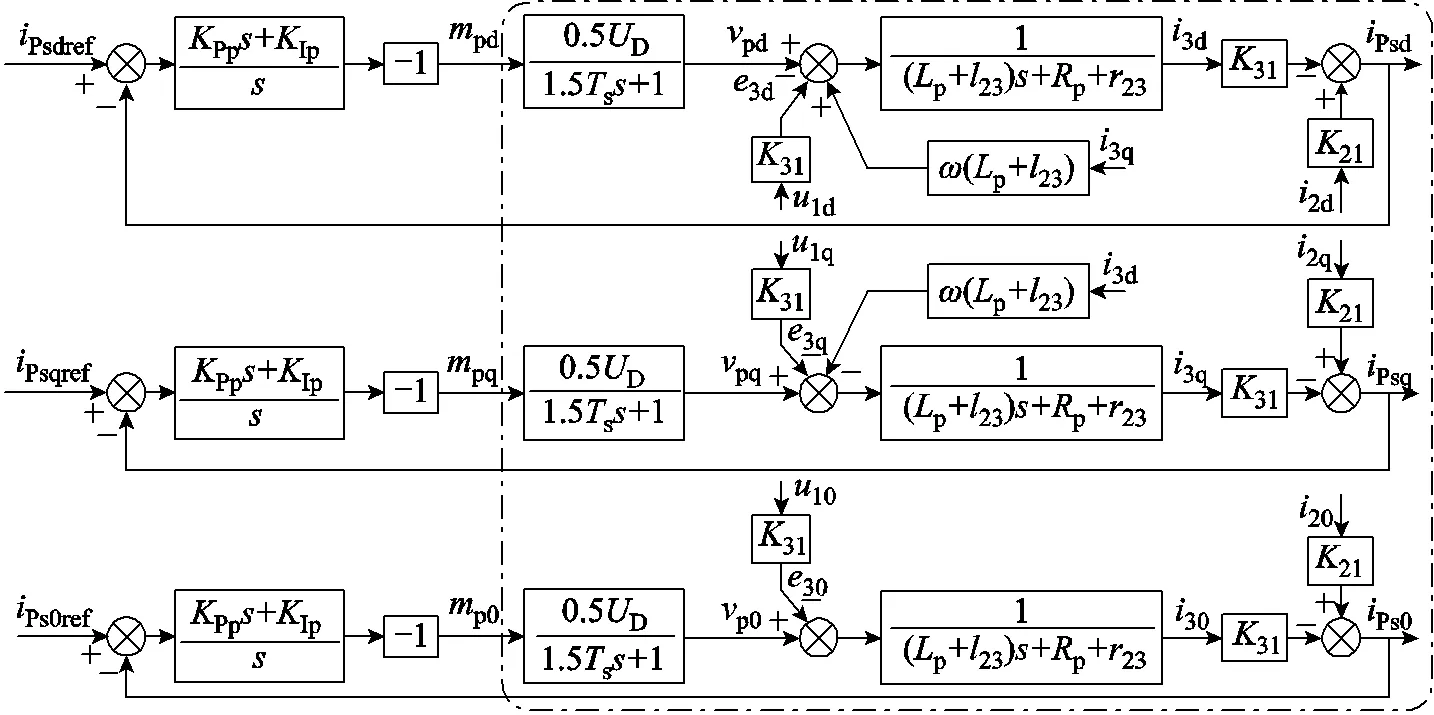
图4 电网电流iPsk闭环控制系统

相比式（1）~式（3），图4更能直观反映影响Psk的扰动量和控制量，从中可以看出，被控对象的主体是个惯性环节。因而本文采用PI控制器，让Psk在同步旋转坐标下直接对其参考信号（如图4所示的Psdref、Psqref、Ps0ref）进行跟踪，从而形成图4所示的HDT电网电流内环控制系统。要实现Psk的正弦单位功率因数控制，一般需要Psdref为常数，而Psqref=0。对于Psdref及Ps0ref的计算，需要综合考虑HDT变换器直流母线电压的稳定控制及上、下电容电压的偏差抑制，这属于HDT外环控制的研究范畴。由于内环、外环时间常数相差很大，可以独立分开设计。由于篇幅所限，本文只分析内环控制系统。

根据式（15）可给出同步旋转坐标系下，从tdq0()到2dq0()模型框图，只是原始框图结构过于复杂，不利于直观反映tdq0()对于2dq0()作用机理，因而本文对其进行化简，化简后的框图如图5中点画线框内部分所示。

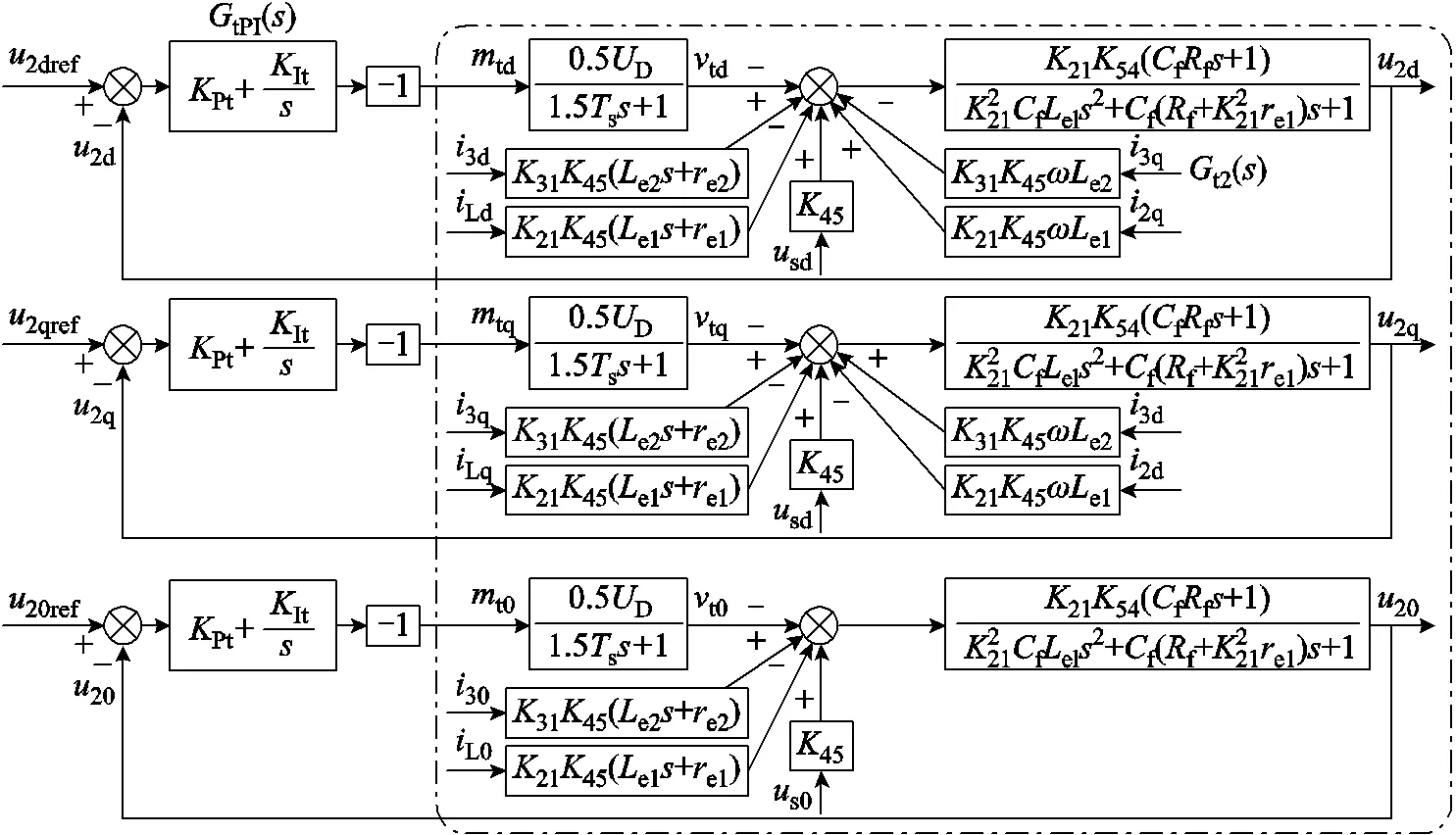
图5 负载电压u2k闭环控制系统框图

图5中

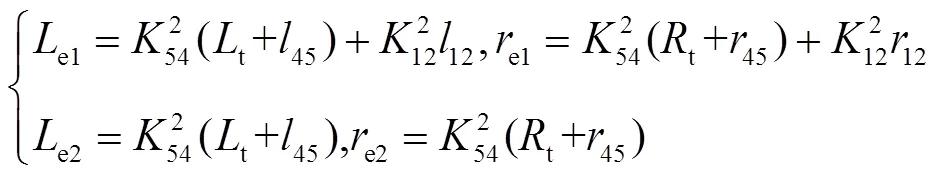
从图5可以看出，负载电压控制模型的主体为一个二阶环节t2()。与电网电流内环控制类似，必须在PI控制器的输出之后乘以-1才能形成负反馈，进而构建负载电压内环控制系统。通过调整f、f和t的值能够改善2k中的高次谐波含量，同时也需要为系统保留足够的稳定裕度。

在图4与图5中，HDT负载电压与电网电流控制环路之间存在耦合，但是由于e1的值并不是很大，因而Psk在e1上产生的压降扰动，相比电网电压的扰动而言往往很小。此外，CVt将负载电压控制稳定之后，W1k的绕组电压基本不会发生大的变化，因而不会再对电网电流造成很大干扰。也就是说，HDT的负载电压及电网电流控制系统之间存在的耦合较弱，因而在实际中可将二者分开独立研究。

4 仿真及实验验证

为验证本文构建的HDT电路拓扑及控制系统的合理性，首先根据图2所示HDT三相电路拓扑，在Matlab的Simulink中搭建HDT的仿真模型，然后对HDT实现负载电压及电网电流的基本功能进行仿真验证。仿真时电网电压模拟真实配电网场景，其他主要参数见表1。

表1 HDT仿真参数

Tab.1 The simulation parameters of HDT

图6给出配电网中出现不正常工况时电网电压及负载电流的波形。具体而言，HDT的负载侧包含桥式不控整流电路，因而负载电流会发生明显畸变。高压侧电网的电压分别出现了骤降（=0.1s，电网电压由120%的额定值骤降为80%的额定值）、突升（=0.16s，电网电压由80%的额定值突升为120%的额定值）及不对称（=0.22s，A、C相电压由120%的额定值骤降为80%的额定值）。显然，如果CVp和CVt均不投入运行（CVp开路，而CVt被旁路），HDT就相当于传统配电变压器，此时负载电压也会相应发生波动，而电网电流也必然出现畸变。而当CVp和CVt参与运行时，负载电压和电网电流的波形如图7所示。

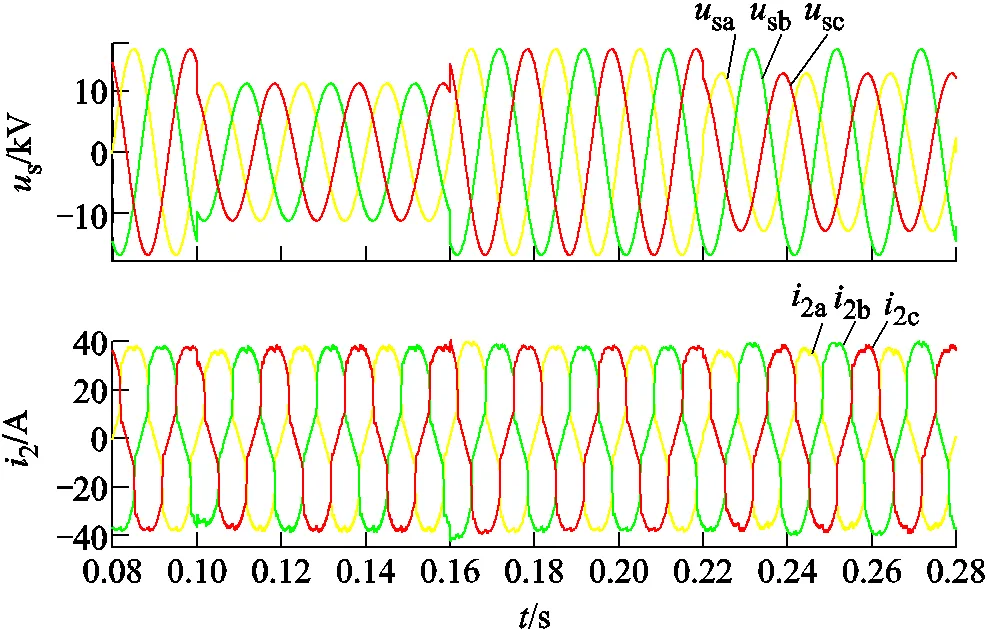
图6 不正常工况下电网电压及负载电流的波形

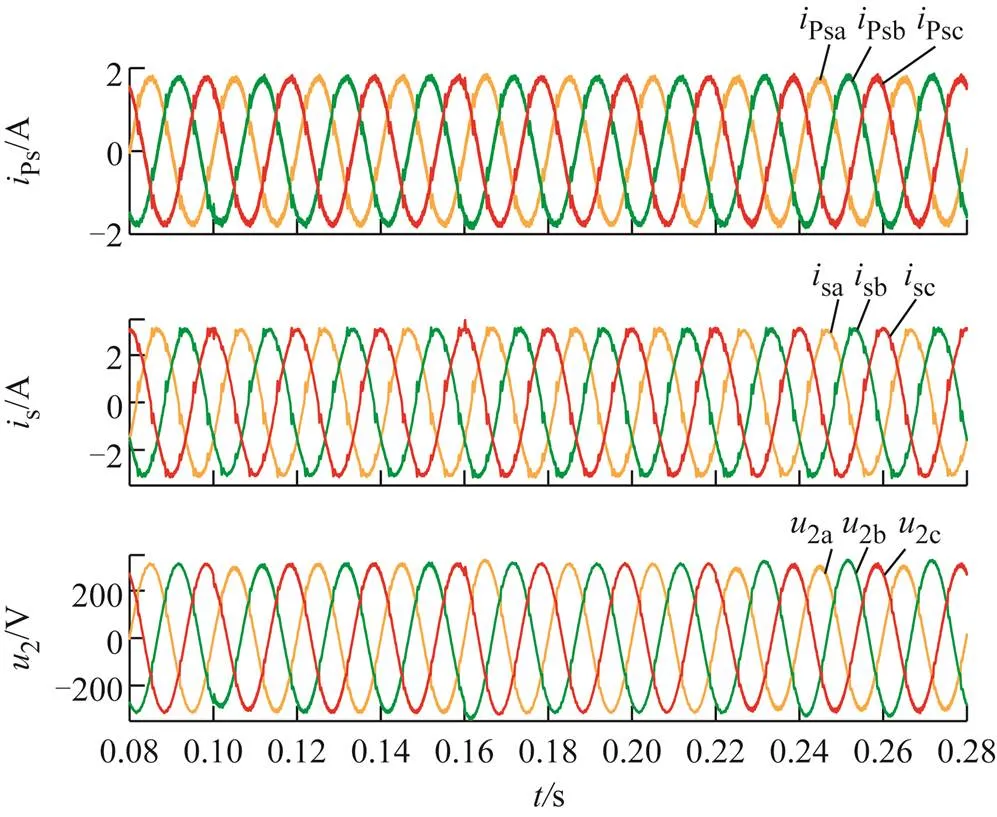
图7 HDT补偿后的电网电流及负载电压波形

从图7可以看出，当电网电压发生突变时，负载电压在经过一个短暂的过程之后便能重新恢复到额定值。此外，HDT网侧绕组的电流能被控制为三相对称的正弦波，进而电网电流也能被控制为正弦波，从而说明本文提出的HDT拓扑及负载电压控制系统是合理的。

图7显示电网线电流sk明显比相电流Psk的纹波要小。具体而言，sk中包含的与开关频率相关的高次谐波含量明显低于Psk。这是因为，本文对CVp进行PWM调制时，三相载波是同一个，这导致Psk中与开关频率相关的高次谐波的三相相位基本相同，因而这些高次谐波也属于零序。当采用三角形联结时，这些高次零序电流无法注入到电网侧，从而只能在高压侧绕组内部流通。从这一点来看，HDT高压侧采用三角形联结还能减小PWM调制引起的高次谐波。这也可以看成本文将HDT高压侧设计成三角形联结的另一个突出优势。

此外，从图7可以看到，电网电压发生突变，负载电流突变均会对负载电压产生不同程度的影响，其中电网电压造成的扰动持续时间明显更长，因而是系统中的主要扰动。对于电网电流控制来讲，畸变负载导致的畸变电流扰动则是影响电网电流控制效果的主要因素。从图7可以看到，虽然电网电流整体上呈现正弦波，但在负载畸变电流突变的短暂瞬间，电网电流会出现一个“尖刺”。这是因为变换器输出电流的最大变化率是有限的，对于突变瞬间，变换器其实是饱和输出状态，无法完全抑制突变扰动带来的影响。此外，出现“尖刺”的时刻其实对应的是负载电流发生突变。由于本例中的负载电流突变已经十分接近理想阶跃信号，而实际控制系统总存在惯性，需要一定的响应时间才能够消除突变扰动带来的影响，因而“尖刺”无法完全消除，在实际中，往往只能通过提高开关频率和降低变换器连接电感等手段进一步减小。

为进一步验证本文提出的HDT电路拓扑及内环控制系统的合理性。本文构建了一个低电压等级的HDT小功率实验样机，具体包括信号采集和检测调理电路、IGBT驱动电路、基于DSP(TMSF28335)的主控电路、HDT主变压器和隔离变压器本体以及由六个桥臂构建的CVp和CVt主电路。用三相可编程电源模拟突变及不对称电网、用整流器及功率电阻模拟畸变负载、而用大容量直流电源支撑直流母线电容。具体样机实物如图8所示，相关实验样机的参数见表2。

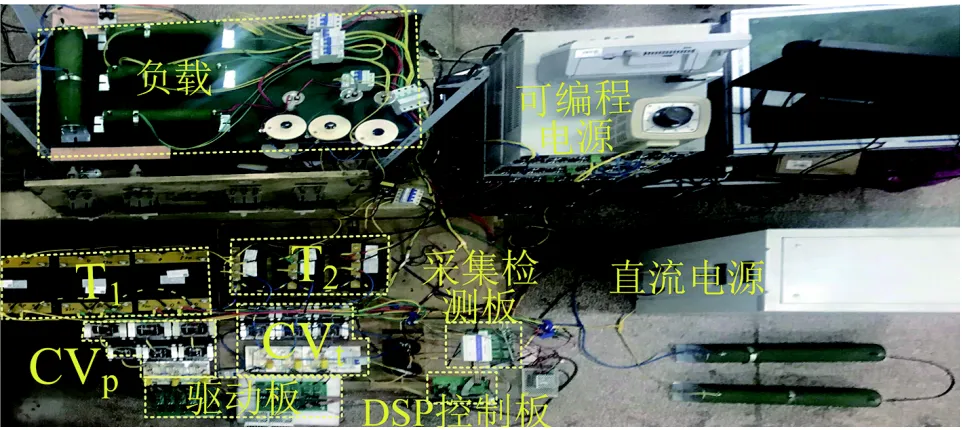
图8 HDT实验样机

基于小功率样机，开展电网电压由80%额定电压突升至120%额定电压再突降回80%额定电压的实验。负载仍包含三相不控整流负载。相关实验波形如图9所示。

表2 HDT实验样机参数

Tab.2 The experimental parameters of HDT

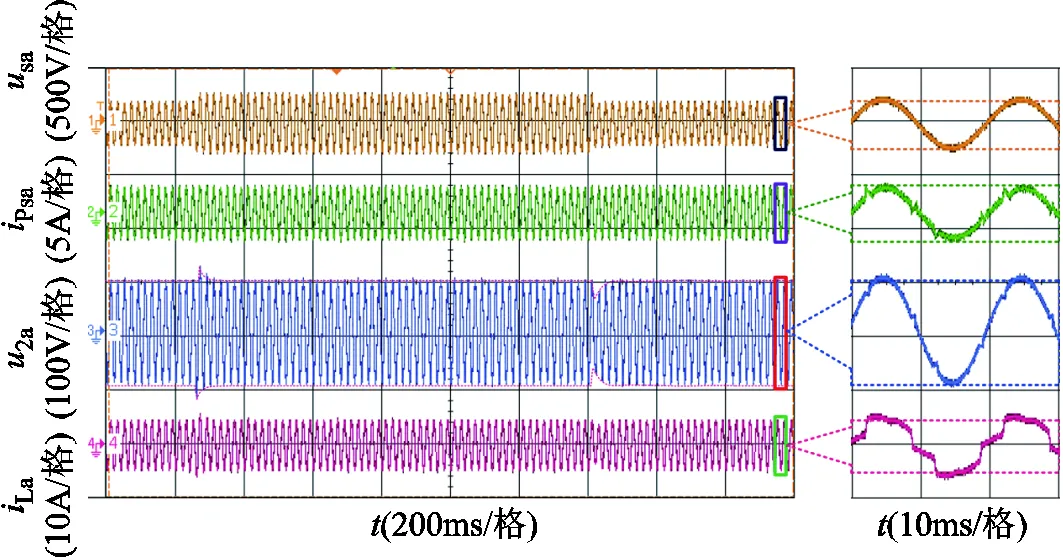
图9 HDT电网电流及负载电压控制实验波形

图9显示，当电网电压突变时，在HDT的控制下，经过很短时间，负载电压便能够恢复到额定值，从而验证了负载电压控制功能的有效性。此外，从右边的局部波形可以看出，当负载电流畸变时，在HDT的补偿作用下，电网电流能够被控制为与电网电压同相位的正弦波形，从而进一步验证了HDT对于畸变电流调控功能的有效性。

5 结论

本文提出一种改进型的HDT电路拓扑，并建立其动态数学模型，基于PI控制器设计HDT电网电流及负载电压闭环控制系统，得到以下结论：

1）将隔离变压器布置于配电网高压侧，而高压侧采用三角形联结方式，其余绕组采用星形中性线引出接法，PWM变换器采用半桥结构的HDT电路拓扑是合理的。

2）基于等效电路导出的HDT动态模型能够清晰揭示HDT的基本工作原理，客观反映HDT运行时遇到的各类扰动。模型指出HDT的负载电压控制系统与电网电流控制系统耦合很弱，可以独立设计。

3）采用PI控制器构建HDT的内环控制系统能满足HDT的对于负载电压及电网电流的基本功能。

[1]Szczeniak P, Kaniewski J. Hybrid transformer with matrix converter[J]. IEEE Transactions on Power Delivery, 2016, 31(3): 1388-1396.

[2]Sastry J, Bala S. Considerations for the design of power electronic modules for hybrid distribution transformers[C]//IEEE Energy Conversion Congress & Exposition, Denver, CO, USA, IEEE, 2013: 1422-1428.

[3]Huber J E, Kolar J W. Applicability of solid-state transformers in today’s and future distribution grids[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 317-326.

[4]Haj-Maharsi M Y, Tang L, Gutierrez R, et al. Hybrid distribution transformer with ac & dc power capabilities: US2010/0201338 A1[P]. 2010-08-12.

[5]巨云涛, 黄炎, 张若思. 基于二阶锥规划凸松弛的三相交直流混合主动配电网最优潮流[J/OL].电工技术学报:1-11[2020-10-23]. https://doi.org/10.19595/ j.cnki.1000-6753.tces.200248. Ju Yuntao, Huang Yan, Zhang Ruosi. Optimal power flow of three-phase hybrid AC-DC in active distribution network based on second order cone programming[J/OL]. Transactions of China Electrotechnical Society, 1-11[2020-10-23].https:// doi.org/10.19595/j.cnki.1000-6753.tces.200248.

[6]周念成, 谷飞强, 雷超, 等. 考虑合环电流约束的主动配电网转供优化模型[J]. 电工技术学报, 2020, 35(15): 3281-3291. Zhou Niancheng, Gu Feiqiang, Lei Chao, et al. A power transfer optimization model of active distribution networks in consideration of loop closing current constraints[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3281-3291.

[7]叶畅, 苗世洪, 刘昊, 等. 联盟链框架下主动配电网电力交易主体合作演化策略[J]. 电工技术学报, 2020, 35(8): 1739-1753. Ye Chang, Miao Shihong, Liu Hao et al. Cooperative evolutionary game strategy for electricity trading stakeholders in active distribution network under consortium blockchain framework[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1739-1753.

[8]颜湘武, 徐韵, 李若瑾, 等. 基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化[J]. 电工技术学报, 2019, 34(10): 2022-2037. Yan Xiangwu, Xu Yun, Li Ruojin, et al. Multi-time scale reactive power optimization of distribution grid based on model predictive control and including RDG regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2022-2037.

[9]范士雄, 蒲天骄, 刘广一, 等. 主动配电网中分布式发电系统接入技术及其进展[J]. 电工技术学报, 2016, 31(增刊2): 92-101. Fan Shixiong, Pu Tianjiao, Liu Guangyi, et al. Technologies and its trends of grid integration of distributed generation in active distribution network[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 92-101.

[10]孔顺飞, 胡志坚, 谢仕炜, 等. 含电动汽车充电站的主动配电网二阶段鲁棒规划模型及其求解方法[J]. 电工技术学报, 2020, 35(5): 1093-1105. Kong Shunfei, Hu Zhijian, Xie Shiwei, et al. Two-stage robust planning model and its solution algorithm of active distribution network containing electric vehicle charging stations[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1093-1105.

[11]Kaniewski J. Hybrid distribution transformer based on a bipolar direct AC/AC converter[J]. IET Electric Power Applications, 2018, 12(7): 1034-1039.

[12]Kaniewski J, Szczesniak P, Jarnut M, et al. Hybrid voltage sag/swell compensators: a review of hybrid AC/AC converters[J]. IEEE Industrial Electronics Magazine, 2015, 9(4): 37-48.

[13]Kaniewski J, Fedyczak Z, Benysek G. AC voltage sag/swell compensator based on three-phase hybrid transformer with buck-boost matrix-reactance chopper[J]. IEEE Transactions on Industrial Electronics, 2014, 61(8): 3835-3846.

[14]Bala S, Das D, Aeloiza E, et al. Hybrid distribution transformer: concept development and field demonstration[C]//2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 2012: 4061-4068.

[15]Burkard J, Biela J. Protection of hybrid transformers in the distribution grid[C]//2016 18th European Conference on Power Electronics and Applications, Karlsruhe, Germany, 2016: 1-10.

[16]梁得亮, 柳轶彬, 寇鹏, 等. 智能配电变压器发展趋势分析[J]. 电力系统自动化, 2020, 44(7): 1-18. Liang Deliang, Liu Yibin, Kou Peng, et al. Analysis of development trend for intelligent distribution transformer[J]. Automation of Electric Power Systems, 2020, 44(7): 1-18.

[17]Radi M A, Darwish M. Var control considerations for the design of hybrid distribution transformers[C]// 11th IET International Conference on AC and DC Power Transmission, Birmingham, UK, 2015:1-9.

[18]Radi M A, Darwish M, Alqarni M. Voltage regulation considerations for the design of hybrid distribution transformers [C]//2014 49th International Universities Power Engineering Conference (UPEC), Cluj-Napoca, Romania, 2014: 1-6.

[19]Liu Yibin, Liang Deliang, Liang Yang, et al. Design and analysis of the compounded control system of hybrid distribution transformer[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018: 3664-3668.

Dynamic Model and Inner Loop Control System of Hybrid Distribution Transformer

Liu Yibin1,2Liang Deliang1,2Wang Yuheng1,2Gao Yachen1,2Zhang Lishi1,2

（1. State Key Laboratory of Electrical Insulation and Power Equipment School of Electrical Engineering Xi’an Jiaotong University Xi’an 710049 China 2. Shaanxi Key Laboratory of Smart Grid Xi’an 710049 China）

Comparing with the traditional distribution transformer, hybrid distribution transformer (HDT) can regulate the partial load power by the integrated PWM converters. Therefore, HDT can not only change the voltage rate and transfer the load power just as the traditional transformer, but also can control the grid current and load voltage in real time. Hence, HDT is a promising equipment for the intelligence of the active distribution network. In this paper, an improved HDT configuration and the three-phase circuit scheme of HDT is presented. In this scheme, the converter with sample topology can be applied and the rated voltages of all the units can be easily determined. Based on the equivalent circuit of the present HDT, the transfer function model is established, then the PI controller is adopted to construct the inner control system of HDT. Both the simulation and experiment are performed in the condition of nonlinear load and fluctuated grid voltage. The results shows that the grid side current can be regulated to be sinusoidal, symmetrical and unit power factor, the load voltage can be controlled to be stable. Which verifies the correctness of the established dynamic model and the presented control strategy.

Active distribution network, equivalent circuit, hybrid distribution transformer, PI controller, transfer function

TM421

10.19595/j.cnki.1000-6753.tces.L90170

陕西省2018年重点研发计划资助项目(2018ZDCXL-GY-07-05)。

2020-06-30

2020-10-29

柳轶彬 男，1988 年生，博士研究生，研究方向为混合式配电变压器磁集成与优化控制。E-mail：yanerwuming@126.com

梁得亮 男，1967年生，教授，博士生导师，研究方向为智能配电网系统协同设计及冗余高效控制。E-mail：dlliang@mail.xjtu.edu.cn（通信作者）

（编辑 赫蕾）