基于主成分分析的温度分布重建优化算法
2021-04-13陈敏鑫孙单勋刘兆宇
陈敏鑫,刘 石,孙单勋,刘兆宇
(1.华北电力大学能源动力与机械工程学院,北京 102206;2.华北电力大学控制与计算机工程学院,北京 102206)
0 引言
传统温度测量方式多以点测量为主,受到现场条件制约,无法布置足够的测点,因此无法获得完整的温度分布信息。利用声波传输的物理特性以及光的辐射特性,研究人员分别研发了基于声学的温度测量方法[1-2]以及基于光学的温度测量方法[3-4]。这两种方法为非接触式测温技术,具有测温范围广、适用场景多的优点。通过结合相应的重建算法,这两种方法能够获得温度分布信息,成为近年来的研究热点。但由于声学设备与光学设备较复杂,且现场条件恶劣,不利于精密设备的安装与调试,这些问题在一定程度上限制了此类方法的应用。
主成分分析作为一种数学分析方法[5]在图像处理、特征提取、数据降维、信号降噪等[6-9]方向应用广泛。综合主成分分析算法的降维特性以及降噪特性,形成基于主成分分析的温度分布重建优化算法,实现了温度分布重建,并进一步提升了重建算法的准确性。
1 算法原理
1.1 主成分分析算法原理
主成分分析算法的实质是通过一组正交向量将原始数据投射至新的空间。投影变换后,新的不相关综合变量替代了原本相关的变量,消除了原始数据的冗余并保留了绝大部分信息。
主成分分析算法的计算步骤如下:
(1)测量数据或经验数据集合构成n×m矩阵,代表n个测点在m个不同工况下的测量或计算数据集合构成的样本数据集。
(2)样本数据集通过去均值处理后,形成归一化矩阵U。
(3)对U的协方差矩阵进行特征分解:
C=UUT=WΛWT
(1)
式中:C为U的协方差矩阵;Λ为协方差矩阵特征根按从大到小排列所构成的对角阵,记为Λ=Diag[λ1,λ2,…λi…,λm],其中λi代表排序后的第i个特征值;W由特征值对应的特征向量构成。
(4)处理后的数据表示为X=WU,X为通过特征矩阵投影后的数据。
实际应用中,通常使用特征值贡献率η表征选取前k特征向量能够保留原始信息的多少。
(2)
1.2 主成分分析算法降维与降噪原理
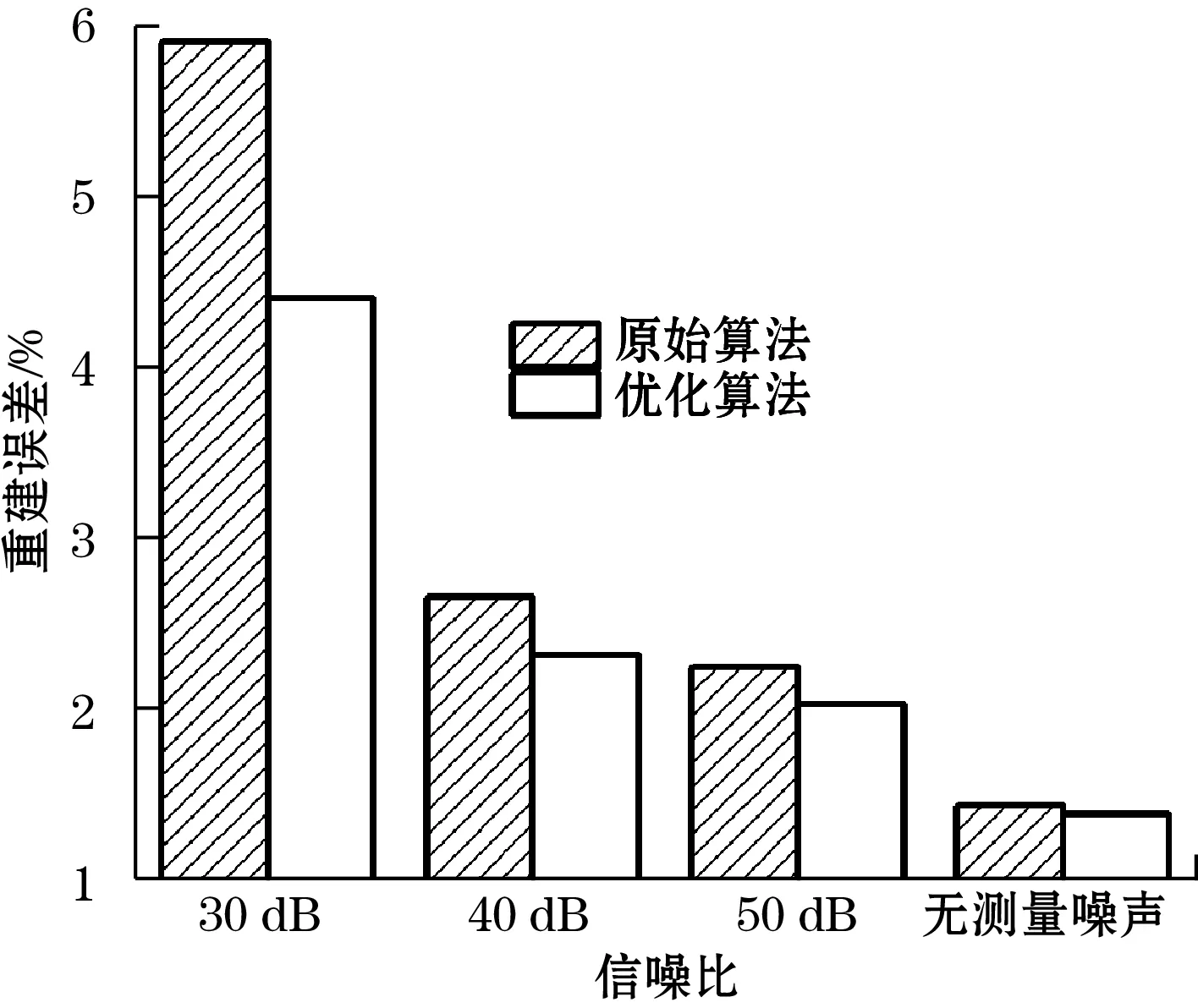
计算特征值贡献率η可知,少数几个特征值的贡献率即可超过99%,这意味着使用少数几个特征向量经过变换后即可保留原始数据的大部分信息。由X=WU可知,当选取前k(k 分析可知,λi(i∈(k+1,m))的特征值贡献率较小,所对应的特征向量包含的原始数据信息较小,且对噪声较敏感。降维过程中通过舍弃贡献率较小的特征值对应的特征向量即可实现对原始数据的降噪处理。 主成分分析算法的降维特性使得利用少量测点通过重建计算获得更多的信息成为可能。由X=WU以及特征矩阵的性质[5]可以推出: ur=WTxr (3) 式中:ur为重建数据;W为特征矩阵;xr为降维后的数据,在重建过程中作为重建系数。 测量过程可以表示为 tM=Mu (4) 式中:tM为测量数据;M为测量矩阵;u为待重建数据。 重建的目标是使ur尽可能接近u,即ur≈u,整理式(3)和式(4)可得: tM≈MWTxr (5) 测量数据tM、测量矩阵M、特征矩阵W均为已知条件。因此重建问题转化为xr的求解问题。根据式(5),xr可以使用最小二乘法求得,重建温度分布ur即可通过计算式(3)获得。 实际应用中,为了比较重建结果,定义重建误差如下: (6) 基于主成分分析的重建算法广泛应用于图像重建[10]、风场重建[11-12]以及空气动力场重建[13]中。 分析式(5)可知,重建过程中测量噪声会影响重建结果的准确性。为降低测量噪声对重建结果的影响,提出基于主成分分析的温度分布重建优化算法,算法流程如图1所示。 图1 优化算法流程 为验证优化算法的可行性以及使用效果,使用Fluent软件构建燃烧仿真模型,进行燃烧仿真实验。仿真模型结构如图2所示。 图2 仿真模型示意图[14] 燃烧仿真实验燃料设定为丙烷,燃料与空气进入燃烧室发生燃烧反应,高温烟气通过尾部烟道排出,设定高度为0.08 m的平面为目标平面,计算对象为目标平面上的温度分布。 仿真实验步骤设定如下: (1)根据实际情况选择Fluent计算模型,设定边界条件。通过不同的边界条件计算获得不同的温度分布数据,构成样本数据集。在样本工况外设立6个重建测试工况。 (2)使用主成分分析算法提取样本数据集特征向量,构成特征矩阵。 (3)在6个实验工况中选取部分数据并添加高斯随机噪声作为测量数据,噪声强度以信噪比(SNR)表示。 (4)分别使用原始算法以及优化算法应用测量数据集进行温度分布重建。 (5)对比重建误差,评价优化算法效果。 为测试优化算法在实际场景的重建效果。进行燃烧实验,燃料为民用液化石油气。设定高度为0.65 m平面为目标平面,在目标平面进行温度数据测量。应用温度测量数据验证优化算法的可行性。燃烧实验台结构及燃烧效果[14]如图3、图4所示。 图3 燃烧试验台 图4 燃烧火焰 燃烧实验步骤设定如下: (1)按照实际物理条件构建燃烧实验台仿真模型,设定不同的初始条件进行模拟计算,以目标平面的仿真数据构成样本数据集。 (2)使用主成分分析算法提取特征向量构成特征矩阵。 (3)进行燃烧实验,燃烧工况设定为燃料入口速度为1.5 m/s,空气速度为7.5 m/s。使用热电偶采集目标平面测点温度值。一部分测量值用于温度重建,另一部分用于重建结果分析。 (4)使用测量值以及添加高斯随机噪声的测量值分别应用原始算法以及优化算法进行目标平面的温度分布重建。 (5)对比重建误差,评价优化算法效果。 对6组重建测试工况进行重建效果分析,为避免添加噪声带来的随机性影响,分别使用原始重建算法以及优化算法进行1 000次重建,求取重建误差的平均值评价算法实际效果,获得普遍性的结论。重建过程中,除算法不同外,特征向量数量、测量数据等影响因素均保持一致。重建测试工况误差如图5~图8所示。 图5 重建误差对比(SNR=30 dB) 图6 重建误差对比(SNR=40 dB) 图7 重建误差对比(SNR=50 dB) 图8 重建误差对比(无测量噪声) 对比重建误差可知,优化算法在不同的测试工况下均能够降低重建误差,且随着噪声强度的增加,优化效果更加明显。因此,针对仿真实验数据,基于主成分分析的温度分布重建优化算法能够提升重建精度。 针对实验工况,选取6个温度测量值作为重建过程中所需的测量数据,向测量数据添加不同信噪比的噪声,考察优化算法在不同噪声条件下的综合表现。同样,由于添加了随机噪声,通过1 000次重建,求取重建误差的平均值来获得普遍性结论,重建结果对比和图9所示。 图9 重建误差对比 由图9可知,在燃烧实验中,在不同噪声条件下,使用优化算法的重建结果误差均小于原始算法。因此,基于主成分分析的温度分布重建优化算法在实际燃烧实验中能够提升重建精度,验证了优化算法在实际应用中的可行性。 利用主成分分析算法的降维特性和降噪特性,提出了基于主成分分析算法的温度分布重建优化算法。在仿真实验以及燃烧实验中进行了验证。对比原始重建算法,优化算法提升了重建过程的抗噪性,在存在测量噪声的情况下明显提高了重建精度。1.3 基于主成分分析的温度分布重建优化算法

2 仿真实验

3 燃烧实验


4 数据分析
4.1 仿真实验数据分析

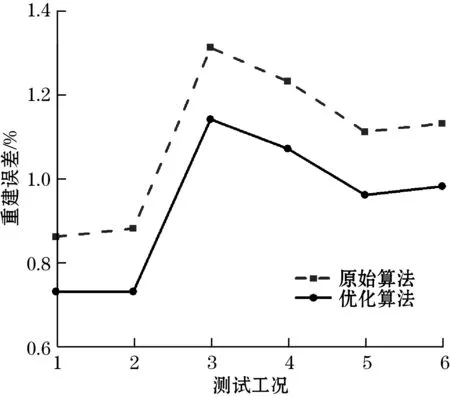


4.2 燃烧实验数据分析
5 结论
