基于Sammon映射和随机森林算法的模拟电路故障诊断
2021-04-13于晨松
于晨松,文 浩
(1.中国石油天然气管道科学研究院有限公司,河北廊坊 065000;2.重庆川仪自动化股份有限公司,重庆 401121)
0 引言
模拟电路在现代电子产业中起重要作用,《国家集成电路产业发展推进纲要》提出了提升先进封装测试业发展水平的要求,模拟电路故障诊断的重要性愈发凸显。模拟电路存在容差,具有非线性,故障诊断难度大。基于人工智能的模拟电路故障诊断方法无需构建数学模型,能够实现故障的识别和定位,因此成为研究热点[1-5]。
使用人工智能进行模拟电路故障诊断的步骤可分为故障特征提取和分类器识别。小波变换常作为提取模拟电路故障特征的工具[6-7],但是小波分解出的子频带中含有冗余信息,会影响故障诊断的准确率,因此需要对其进行降维处理。常用降维方法有主元分析[8]和因子分析[9],但这些方法在进行数据降维时仅去除数据之间的线性相关性,不能保持原有数据的流型结构。模拟电路故障诊断的另一个重要部分是构造分类器,常用方法有神经网络[10]、支持向量机[11]和决策树[12]。但是神经网络迭代速度慢且易陷入局部最优解;支持向量机对噪声敏感,影响故障诊断率;决策树是一个递归过程,在计算过程中易出现过度拟合的情况。
Sammon映射[13]是一种非线性映射,它通过非线性变换,能够直观地在低维空间展现原数据间的结构信息,得出高维数据在低维的相互关系,是一种“几何图形降维”的投影法。Sammon映射对数据降维时,能够保留原数据中的重要信息,适合模拟电路故障特征的优化。随机森林[14]是一种新兴的、高度灵活的机器算法,它的本质是集成多个决策树的分类器。随机森林的输出结果是由单个决策树的输出类别的众数决定的,在分类过程中,它能够获取内部生成误差的无偏估计,具有较强的泛化能力。
本文提出一种基于Sammon映射和随机森林的模拟电路故障诊断方法。首先对电压信息进行小波包分解,提取各子频带的能量值作为故障特征,然后用Sammon映射对故障特征进行降维优化,用优化后的故障特征训练随机森林,得出模拟电路的故障模式,最后用巴特沃斯带通滤波器对本文方法进行实验验证。
1 故障特征提取
小波变换能够通过平移母小波和缩放小波宽度,得出信号的时间和频率特性。小波包分解是小波变换的一种形式,它可同时对信号的低频和高频部分进行分解,能够根据被分解信号的特性,自适应地选择相应频带,使之与信号频谱相匹配,增强了对信号的处理能力,小波包分解图如图1所示。

图1 小波包分解图
小波包函数可定义为
(1)
式中:m为振荡参数,m=0,1,2,…;j为尺度参数,j∈Z;k为平移参数,k∈Z。
由于采集到的电压信号V是离散的,需对其进行离散小波包分解和重构,公式如下:
(2)
(3)
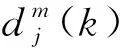
电压信号V经小波包分解后会得出子频带,需求其能量值Eij作为故障特征,计算公式为
(4)
式中:j=0,1,…,2i-1;N为信号的长度。
全部Eij构成小波包能量谱。
E=[Ei,0,Ei,1,…,Ei,j]
(5)
将得到的子频带能量谱构造成矩阵E,即得到模拟电路的故障特征。
2 Sammon映射
Sammon映射能够真实地刻画原空间数据点的距离信息。在保持数据内部结构不发生变化的基础上,它能够将高维的输入空间近似地转化为低维空间,得出原数据间的结构信息。因此在使用Sammon映射进行降维时,可以保留原数据的重要信息,使降维结果和故障特征具有高度的相似性。

(6)
Sammon映射是在保持高维空间数据不变的基础上,寻找映射:
f:X∈RD→Y∈Rd
(7)
这个映射使用梯度迭代运算得到最小化的目标函数,从而得出数据降维后的低维表示:
(8)
3 随机森林
随机森林算法是基于模式识别的学习算法,它的本质是一个包含多个决策树的分类器。随机森林通过样本训练,能得到多个包含样本特征的随机决策树,从而完成目标分类。随机森林运算速度快、泛化性能强,适合作为模拟电路故障诊断的分类器。
随机森林通过Bootstrap 法重采样得到多个训练集,只需要通过少量的样本就可以估算出参数的分布特征。随机森林在构建决策树时,采用随机选取分裂属性集的方法,具体的流程如下:
(1)利用 Bootstrap方法重采样,随机产生T个训练集S1,S2,…,ST。
(2)每个训练集均生成各自的决策树C1,C2,…,CT,在每个内部节点选择属性前,从M个属性中随机抽取m个属性作为当前节点的分裂属性集,并以这m个属性中最好的分裂方式对该节点进行分裂。
(3)让每棵树都完整成长,不进行剪校。
(4)对于测试集样本X,利用每个决策树进行测试,得到对应的类别C1(X),C2(X),…,CT(X)。
(5)采用投票的方法,将T个决策树中输出最多的类别作为测试集样本X所属的类别。
随机森林流程图如图2所示。

图2 随机森林流程图
4 仿真实验及分析
在PSPICE 9.2软件中绘制电路图,并通过仿真得到电压信号。首先对电压信号进行小波包分解,提取子频带的能量值作为故障特征,然后用Sammon映射对其进行优化,得到训练样本集和测试样本集,最后将其输入随机森林进行网络训练和故障诊断,具体的流程如图3所示。

图3 诊断流程图
4.1 电路仿真
本文使用ITC’97 Benchmark电路中[16]的巴特沃斯带通滤波器电路进行仿真,该电路是可用于评估算法性能的标准电路。在PSPICE 9.2中绘制电路图,如图4所示。

图4 巴特沃斯带通滤波器电路图
巴特沃斯带通滤波器的Vin处输入正弦信号,其幅值为1 V,频率为1 kHz,用↑表示超过元件标称值的故障,用↓表示低于元件标称值的故障,电路共设置包括正常状态在内的11种故障模式,具体故障值设定见表1。
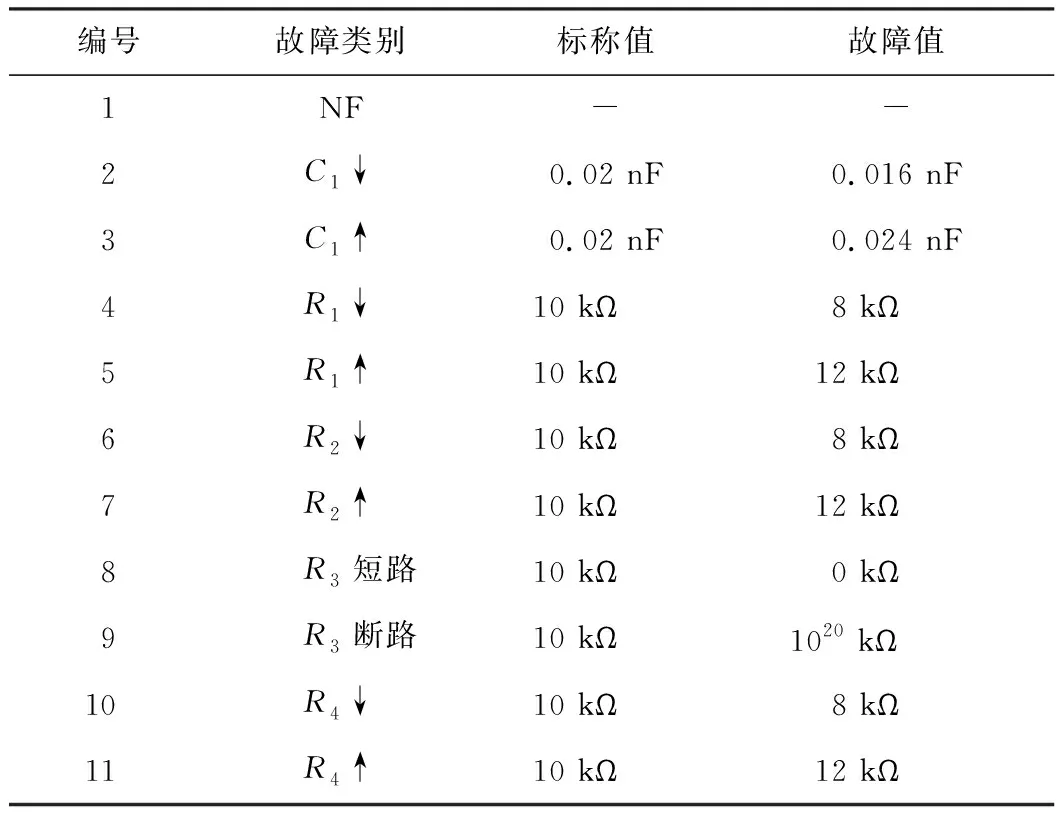
表1 巴特沃斯带通滤波器故障模式表
使用PSPICE 9.2软件对巴特沃斯带通滤波器电路的正常模式和故障模式进行50次Monte Carlo仿真,在输入端输入激励信号,在输出端采集300点电压信号。仿真结束后,可以得到11组包含50个电压信号的样本数据,得到的电压信号如图5所示。

图5 电压信号波形图
4.2 提取故障特征
Db3小波基消失矩阶数大,能够更好地将电路故障信息分解到子频带,提高诊断精度[7],因此本文使用Db3小波基对11组电压信号进行三层小波包分解。电压信号经小波包分解会得到8个子频段,使用式(4)提取子频段的能量谱,构成新的特征向量,如图6所示。

图6 部分故障特征图
计算出的小波包能量谱仍具有冗余信息,这在增加诊断消耗的同时会降低模拟电路的故障诊断率,因此本文用Sammon映射对其进行优化。Sammon映射可以保留高维数据间的结构信息,并给出一个有效的低维表示,可以有效降低故障特征中的冗余信息。
在使用Sammon映射前,计算得到故障特征的本质维数为3,因此能把8维的故障故障特征降到3维。这有利于减少网络训练时间,提高模拟电路故障诊断的效率。经Sammon映射优化后,得到的故障特征如图7所示。由图7可知,经Sammon映射优化后,故障特征具有良好的区分度。
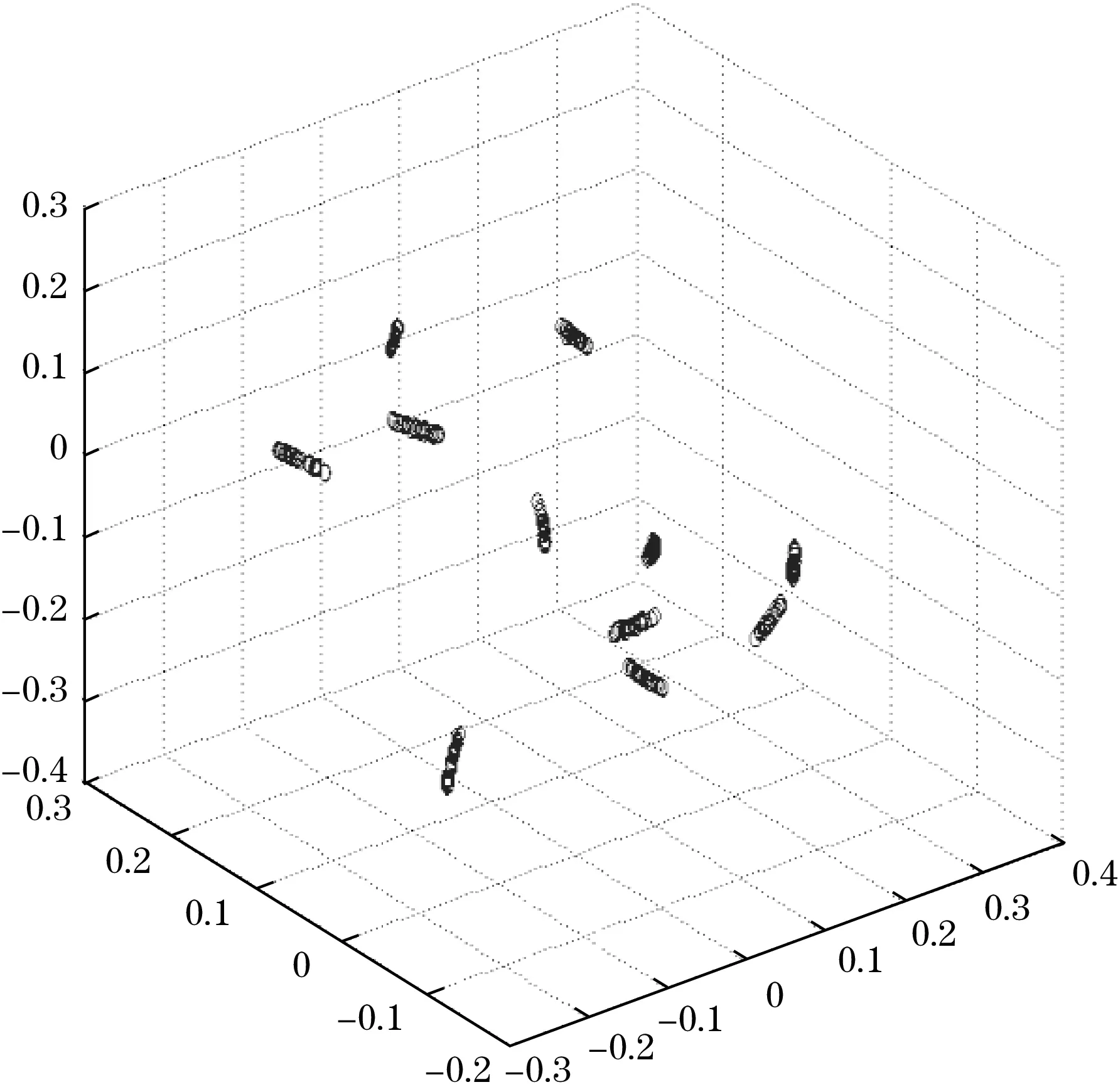
图7 特征向量三维图
4.3 故障诊断
经Sammon映射优化后,故障特征为三维输入。为确定随机森林中决策树的棵数,设定其范围为50~1 000之间,间隔为50,得到的分类准确率和决策树棵数的关系如图8所示。由图8可知,综合随机森林的判断准确率和运行效率,随机森林的决策树棵数设定为300棵。

图8 随机森林准确率图
为了证明Sammon映射对故障特征的优化作用,本文将未经优化的小波包能量谱输入随机森林作为对比实验。首先将50组故障特征分成30组的训练样本和20组的测试样本,然后将训练样本输入随机森林对其进行网络训练,最后用测试样本对训练好的随机森林的故障诊断能力进行检验,得到的实验结果如图9所示。

(a)未经优化准确率为85%
将图9中的诊断数据进行整理,得到的结果如表2所示。

表2 故障诊断结果表
由表2可知,未经Sammon映射的小波包能量谱作为故障特征输入随机森林时,得到的故障诊断率为85.5%;经Sammon映射优化的故障特征输入随机森林后,得到的故障诊断率为97.7%。这说明Sammon映射能够去掉小波包能量谱中的冗余信息,有效对故障特征进行优化,提高模拟电路故障诊断的准确率。
将本文方法和其他故障诊断方法进行对比,结果如表3所示。

表3 诊断率对比表
由表3可知,本文方法相比于小波包与支持向量机和混合粒子群优化BPNN,准确率更高,在模拟电路故障诊断中具有更佳的优越性。
5 结束语
针对模拟电路的故障识别定位的难题,本文提出了基于Sammon映射和随机森林的故障诊断方法。首先使用小波包对得到的电压信号进行分解并提取故障特征,然后用Sammon映射对故障特征进行优化,最后通过随机森林进行故障诊断。由实验可知,本文方法具有较高的故障诊断准确率,为实现模拟电路的故障定位和识别提供了一种新的选择。
