SVPWM教学研究之空间矢量
2021-04-13黎灿兵
佘 焱, 王 勇, 黎灿兵, 孙 佳
(上海交通大学 电力传输与功率变换控制教育部重点实验室,上海200240)
0 引言
空间矢量脉宽调制SVPWM(Space Vector PulseWidth Modulation)将电压型逆变器输出的基本空间电压矢量合成需要的参考空间电压矢量,是“电力电子技术”教学中的重要内容,在电机控制和并网技术等领域中有重要应用。但是,目前在有关的教材和文献对SVPWM的讨论中存在一些不同的观点,特别是空间矢量的定义不统一[1~5],概念的性质不清楚,影响到后面SVPWM的教学,所以,对空间矢量的定义及其性质进行较为透彻的研究与分析,在SVPWM的教学中十分重要。我们结合有关教材的编写,对此进行了一些探讨和澄清,在此求教于大家。
1 空间矢量定义
目前空间矢量的定义存在三个问题:一、定义与感应电机等应用场景经常没有很好的区分,逻辑上存在一些混乱;二、很多定义不够严谨,比如,有时候把三相正弦交流电的空间矢量作为空间矢量的定义,造成教学的时候学生理解困难;三、定义不统一,目前至少存在三种空间矢量的定义,甚至有时候用3s-2s坐标变换来定义空间矢量。本文给出空间矢量的严格统一定义,将其应用到三相正弦交流电和逆变器。
1.1 定义
如图1所示,首先建立单位矢量αβ和单位矢量U、V、W,其中αβ正交,U、V、W相互之间差120度,U和α重合。

图1 三相电压的空间矢量
定义对于给定的三相电压vU、vV、vW,称
Vs=k(vUU+vVV+vWW)
(1.1)
为三相电压vU、vV、vW的空间矢量,其中k为常数。上述求和为矢量求和运算。
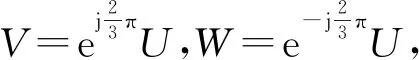
(1.2)
通常对k的选择有三种,分别对应空间矢量的三种定义,下一节我们对这三种定义进行探讨。
注意到:①空间矢量为一矢量,等于(1.1)式右边三个矢量之和。②我们的定义针对所有三相电压,并不需要依赖感应电机的应用场景,也不只针对三相正弦交流电,所以,可以广泛地适用于所有应用领域。③该定义还能很简单地推广到多相电压情形。
1.2 三相正弦交流电的空间矢量
对于三相正弦交流电:
vU=Umcosωt
(1.3)
(1.4)
(1.5)
代入式(1.1)可得其空间矢量:
(1.6)
可见三相正弦交流电的空间矢量以角频率ω旋转。
1.3 逆变器输出的基本空间矢量
三相电压型逆变器的拓扑结构如图2所示。

图2 三相电压型逆变器
显然有:
vUn=vUN+vNn
(1.7)
vVn=vVN+vVn
(1.8)
vWn=vWN+vWn
(1.9)
下面计算vUn、vVn、vWn的空间矢量。
Vs=k(vUnU+vVnV+vWnW)
=k((vUN+vNn)U+(vVN+vNn)V+(vWN+vNn)W)
=k(vUNU+vVNV+vWNW)+kvNn(U+V+W)
=k(vUNU+vVNV+vWNW)
(1.10)
即vUn、vVn、vWn的空间矢量等于vUN、vVN、vWN的空间矢量,下面只需计算vUN、vVN、vWN的空间矢量。
定义单极性二值逻辑开关Sj(j=U,V,W),当上桥臂开通,下桥臂关断时,Sj=1;当下桥臂开通,上桥臂关断时,Sj=0:

(1.11)
图2所示的三相逆变器共具有8种开关组合模式【000,100,110,010,011,001,101,111】。因为sv=1时,vUN=VD;sV=0时,vUN=0,所以:
vUN=SN·VD
(1.12)
类似有:
vUN=SN·VD
(1.13)
vWN=SW·VD
(1.14)
将8种开关组合代入到式(1.12)~(1.14)三式中, 得到输出电压的瞬时值vUN、vVN、vWN,并将vUN、vVN、vWN代入到式(1.1),可以得到对应的8个矢量Vi(i=0~7)及其模。表1表示了不同开关组合时的输出电压值和对应的矢量Vi。
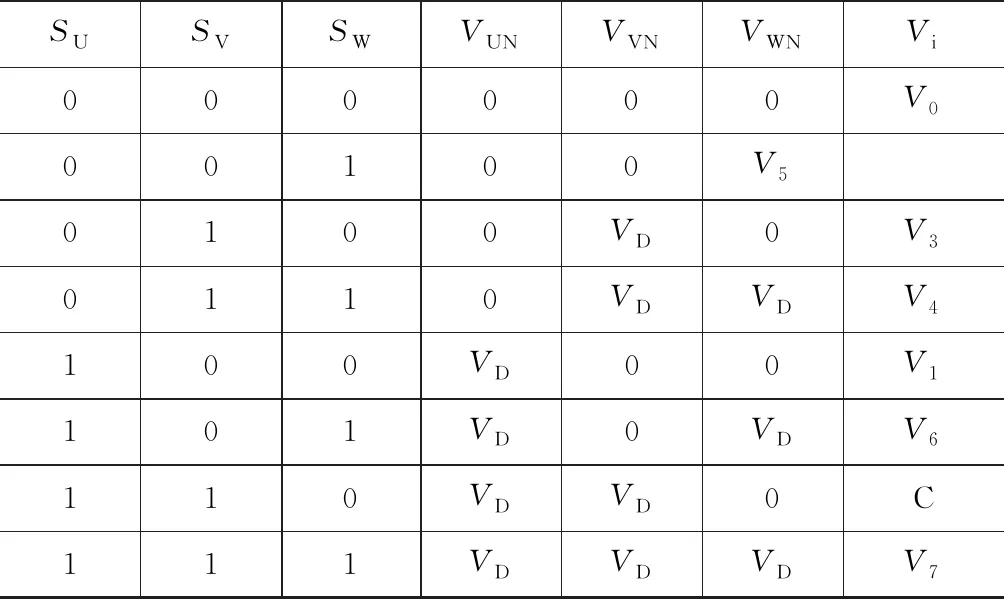
表1 不同开关组合时的输出电压值
三相三线电压型逆变器6个基本空间矢量Vi及零矢量为:

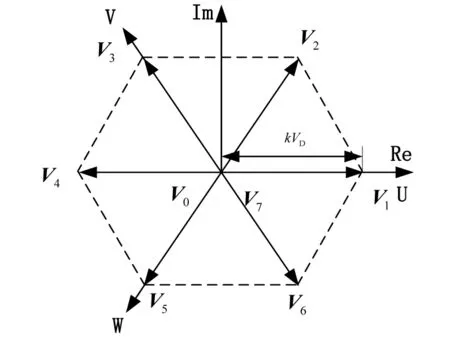
图3 6个基本矢量构成的正六边形
2 空间矢量的性质
本节证明空间矢量本质上是坐标变换,由此引出空间矢量的坐标变换定义。在并网逆变器控制中,SVPWM常常作为3s-2s坐标变换的逆变换使用。同时还指出空间矢量不能定义三相电压的原因。
2.1 空间矢量是3s-2s坐标变换
注意到式(1.1)等号左右两边的矢量相等等价于其实部和虚部分别相等:
(2.1)
(2.2)
上式写成矩阵形式:

(2.3)
可见空间矢量的本质是3s到2s的坐标变换。所以,空间矢量也可以用坐标变换来定义。

2.2 空间矢量不能作为三相电压的定义
因为空间矢量本质上是3s到2s的坐标变换,而该变换为非满秩不可逆变换。即,不同的三相电压可能有相同的空间矢量。所以,由空间矢量不能唯一确定三相电压。例如vU、vV、vW与vU+v、vV+v、vW+v的空间矢量相等。
2.3 SVPWM作为坐标变换的逆变换
对于给定的参考空间矢量,由SVPWM算法,可以得到基本空间矢量与其对应。SVPWM可以看成由参考空间矢量到基本空间矢量的一个映射,而基本空间矢量又与逆变器输出三相电压一一对应,所以,SVPWM可以看成从参考空间矢量到逆变器输出三相电压的映射。因为坐标变换是三相电压到空间矢量的映射,这使得SVPWM可以作为坐标变换的逆变换。
当空间矢量作为坐标变换的逆变换时,空间矢量的k应与坐标变换的k保持一致。
3 结语
SVPWM是“电力电子技术”教学的重要内容,本文针对现存教材对这部分内容阐述不够清晰统一等问题,结合SVPWM的最新研究进展[6~7],对空间矢量的基本概念、应用、性质进行了较为深入的研究和探讨,为后续SVPWM教学打下基础。
