基于BP神经网络的左心室心肌组织参数反演方法的研究*
2021-04-13张其帅杨克虎李录贤
张其帅,杨克虎,李录贤△
(1.西安交通大学航天航空学院 机械结构强度与振动国家重点实验室 陕西省先进飞行器服役环境与控制重点实验室,西安 710049;2.西安电子科技大学通信工程学院 综合业务网理论与关键技术国家重点实验室,西安 710071)
1 引 言
近年来,随着心脏力学研究的不断深入,人体心肌的组织特性逐渐成为表征心脏健康状态的一个重要指标[1-2]。研究表明,相比于健康者,舒张型心力衰竭患者或心肌梗死患者的心肌硬度要高很多[3-5],因此,开展心肌组织特性研究对心脏疾病的临床诊断具有重要意义。
限于人体心肌组织标本很难获得[6-7],研究者对心肌组织特性的研究主要依赖于动物实验模型,即假设心肌组织特性符合一种特定本构关系,通过对标本的单轴拉伸、双轴拉伸或剪切试验获取应力应变曲线,确定本构方程中的材料参数[8-10]。此方法虽可定量分析心肌的组织特性,但离体失活的心肌测量结果与具有血流特性的真实心肌特性之间存在明显的差异[3],加之动物心肌组织与人体心肌组织存在差异,其结果的可参考性也一直存在争议[5]。
针对获取心肌组织特性存在的困难,本研究提出一种基于智能优化算法的反演方法。采用左心室动态响应数据建立参数反演的BP(back propagation,BP)神经网络结构,映射左心室动态响应与心肌组织参数之间的非线性关系;将个体患者的临床非侵入式左心室诊断数据输入到已训练好的BP神经网络,反演出测试者的心肌组织参数。该基于BP神经网络的反演方法在获得心肌组织特性的同时,还能满足临床心脏疾病检测的快速时间响应需求。
2 左心室的有限元建模
2.1 左心室的几何模型
本研究中的几何模型来自人体左心室(left ventricle,LV)的内外膜CT扫描数据。首先沿左心室轴向进行等间距(5 mm)扫描,获得12个不同截面的左心室CT影像,见图1(a)—(l)。

图1 左心室的CT截面影像Fig.1 CT Image of LV sections
再利用Matlab语言编写图像识别程序,提取CT影像中的左心室内外膜位置点,分别见图2(a)、(b)。
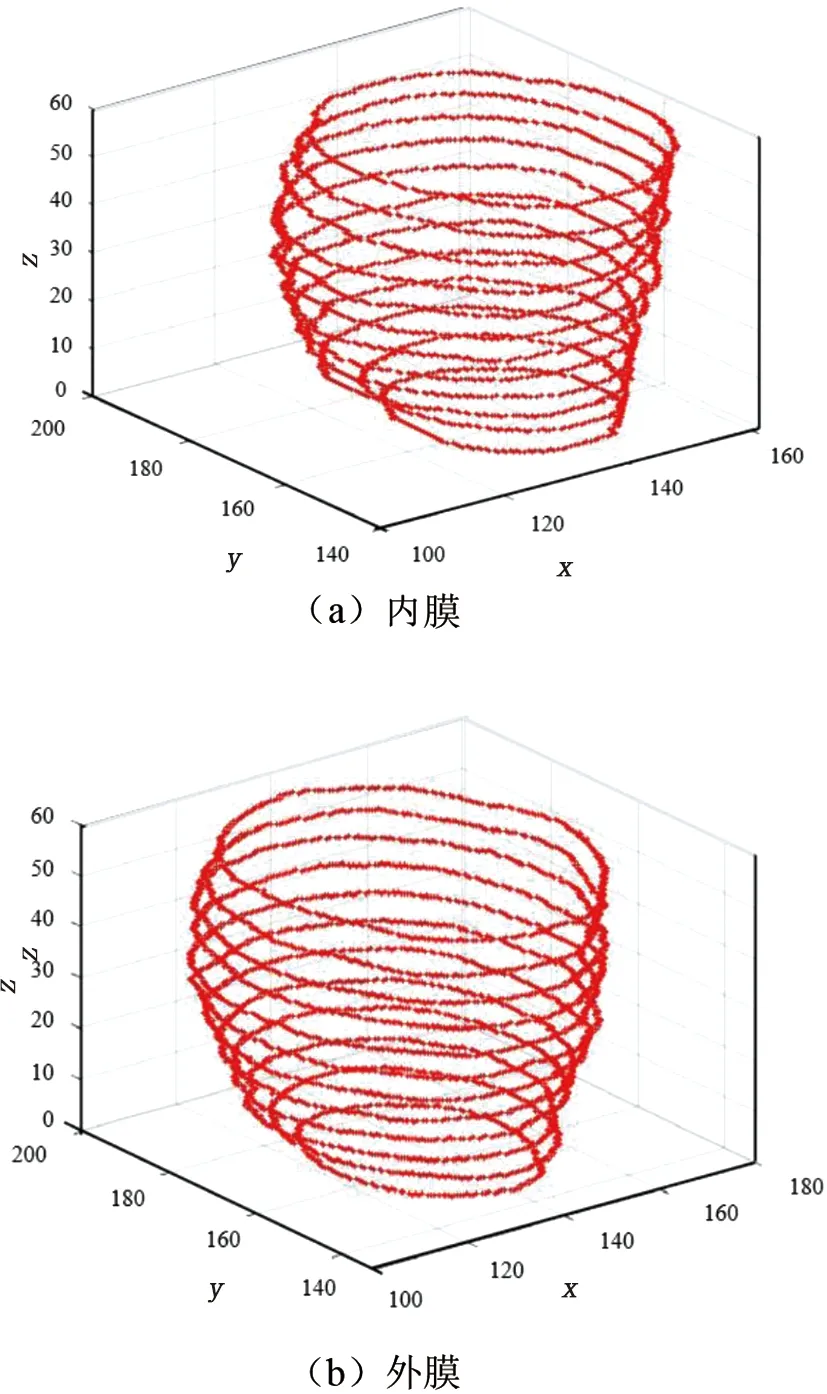
图2 Matlab图像识别的左心室CT数据Fig.2 The LV CT Data recognized by Matlab
进一步,通过SolidWorks软件,建立左心室的几何模型,见图3。
2.2 左心室的有限元模型
经计算图1中12个不同截面的CT影像,左心室心肌的平均厚度为5.65 mm,第5~12层共8个截面的平均厚度在6 mm左右。基于图3的左心室几何模型,抽取其中面,形成左心室的壳结构,取6 mm作为壳的厚度。利用Abaqus软件自动划分网格功能,控制左心室模型边界布种密度和网格属性,得到图4所示的壳结构有限元网格,共计4 084个S4R壳单元和60个S3R壳单元,节点总数4 150个。
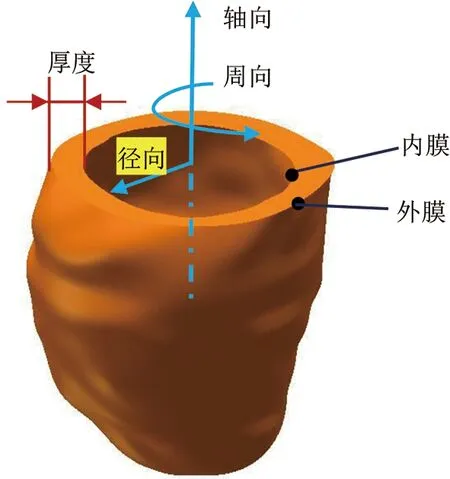
图3 基于CT影像的左心室几何模型Fig.3 CT image based geometric model of the LV

图4 左心室有限元模型Fig.4 Finite element model of the LV
3 BP反演数据的建立方法
BP神经网络可以映射任意复杂的非线性函数关系[11-12],本研究运用BP神经网络技术反演心肌组织的性能参数,为此,我们对左心室先进行动态有限元分析,以获得BP神经网络的训练数据。
3.1 心肌组织特性
人体心肌是一种具有特异性质的超弹性不可压天然生物材料。从心肌性能的不同特点出发,不少学者建立了心肌组织性能的描述方法,但至今仍没有一种被广泛认可的表达形式。本研究聚焦于反演方法研究,将心肌视为各向同性超弹性材料,对于实际的各向异性心肌组织,在增加参数数目和反演运算量后,本研究方法仍将适用。
对于各向同性超弹性材料,我们选取最常用的不可压Mooney-Rivlin模型[13],其能量密度函数的表达式为:
(1)
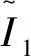
3.2 受载分析
心脏的周期性收缩与扩张来源于两个因素,一个是心肌受到心电刺激所产生的主动力,另一个是心脏变形受到内部血液压力反作用而产生的被动力[14]。主动力可通过心肌兴奋力σ随兴奋时间t的变化表示为[14]:
(2)
其中τ为不同时刻的传播时序,Te为兴奋周期,σmax为肌小节兴奋力。本研究取与文献[15]相同的参数,即σmax=53.3 kPa和Te=0.353 s。兴奋时序τ一般较难确定[15],本研究取为0。左心室被动力通过动脉压力予以间接获得[7, 15]。一个心动周期内左心室的受载变化见图5。
3.3 BP输入数据的获取
给定心肌组织参数(也就是BP神经网络的目标向量),对左心室有限元模型心底位置施加固支约束,对内外表面分别施加图5中均布的径向被动力和周向主动力,利用Abaqus软件的Explicit求解器,对左心室一个心动周期0.8 s内的变形过程进行分析[15],得到图6所示的变形过程。可以看出,在一个心动周期内的不同时刻,左心室发生了明显的收缩变形,与真实的左心室运动过程十分类似。
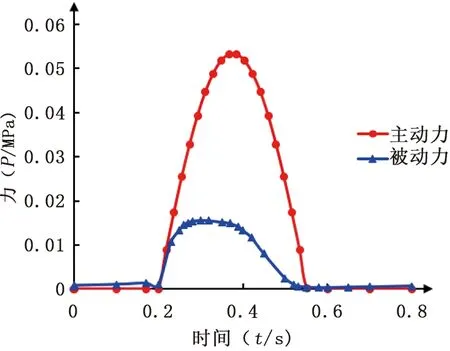
图5 左心室受载随时间变化关系[15-16]Fig.5 Variation of loading with time for the LV[15-16]

图6 收缩过程中左心室几何形态变化Fig.6 Geometric variation of the LV during a period of contraction
通过左心室的有限元分析,还可得到左心室任意位置的变形。本研究选取左心室Z=8、20、32、44 mm的四个典型截面位置(见图7),将心动周期内某些时刻的径向位移值作为BP神经网格的输入向量。
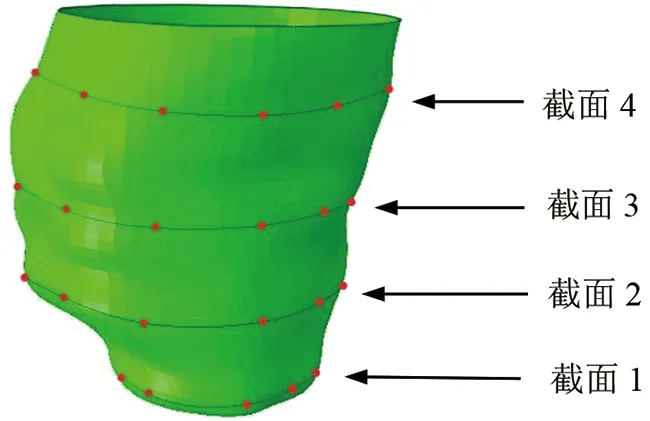
图7 取样点在左心室结构中的位置分布Fig.7 Distribution of sampling points in LV structure
4 基于BP神经网络的心肌组织参数反演
4.1 BP神经网格反演的基本思想
BP神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一[17]。BP神经网络由输入层、隐含层和输出层组成,在不限制隐含层节点的情况下,三层的神经网络理论上可逼近任意非线性函数关系式[18],见图8。
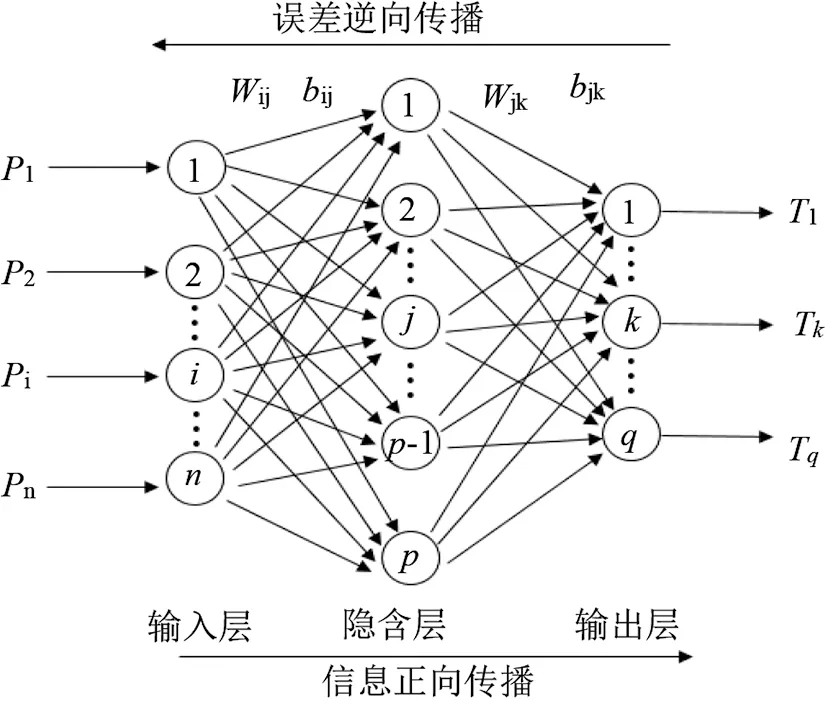
图8 BP神经网络拓扑结构Fig.8 The topologic structure of BP neural network
基于BP神经网络的参数反演就是建立响应与参数之间的非线性关系,包括以下基本步骤[19]:
(1)确定待反演参数的取值范围;
(2)在参数取值范围内均匀分散取值获得目标向量;
(3)通过响应获得输入向量;
(4)将输入、目标向量输入BP神经网络进行训练;
(5)利用BP神经网络输入和输出的映射关系,将人体左心室诊断数据输入神经网络反演参数。
上述5个步骤又可概括为BP神经网络的建立(包括步骤(1)—(4))和参数反演(即步骤(5))两部分,下面予以分别研究。
4.2 BP神经网络的建立
4.2.1输入向量和目标向量的建立 由文献[20]可知,以Mooney-Rivlin模型表示的正常左心室心肌组织参数分别为C10=0.178 MPa和C01=3.989 MPa,密度为1.370×103kg/m3。据此,两个参数的可能取值范围分别确定为0.100≤C10≤0.300和3.000≤C01≤5.000;基于正交试验设计方法,对两个参数进行组合,取值C10=0.100、0.150、0.200、0.250、0.300,C01=3.000、3.250、3.500、3.750、4.000、4.250、4.500、4.750、5.000,共形成45组不同的心肌组织参数组合,将它们作为BP神经网络训练的目标向量。
取心动周期内t=0.2 s(收缩初期)、t=0.4 s(收缩中期)和t=0.6 s(收缩末期)共3个特征时刻左心室4个典型截面上的径向位移作为BP神经网络的输入向量。每个截面上等间隔地取12个点,共计48个点。不同心肌组织参数下的左心室模型对应不同的径向位移,形成45组训练样本。在3个特征时刻下,得到对应时刻下的45组训练样本,分别见表1、表2、表3。
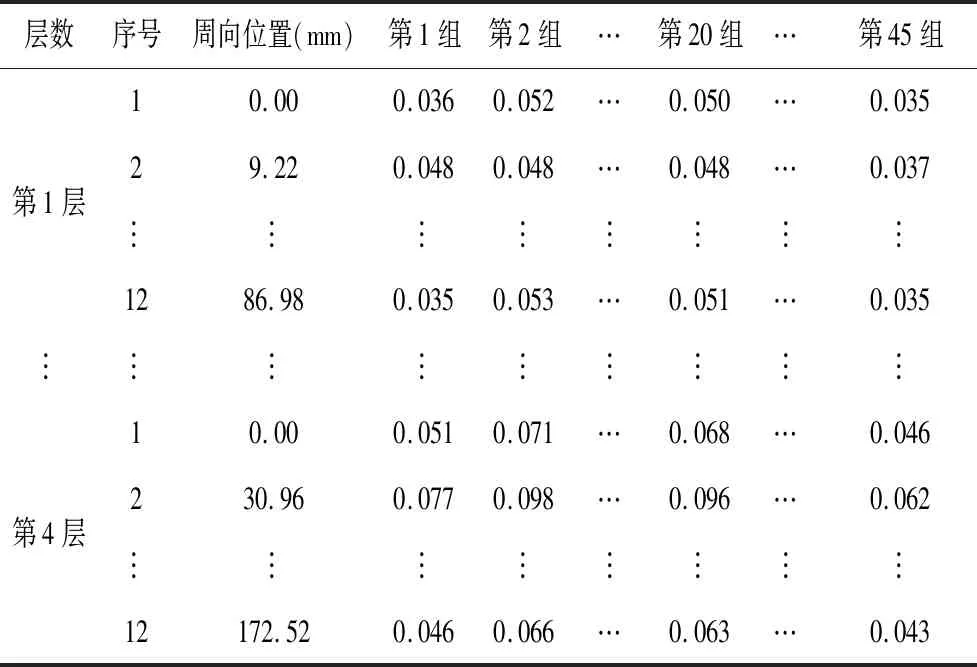
表1 不同心肌组织参数对应的左心室径向位移(t=0.2 s)Table 1 Radial displacements at the LV from different myocardial tissue parameters (at t=0.2 s)
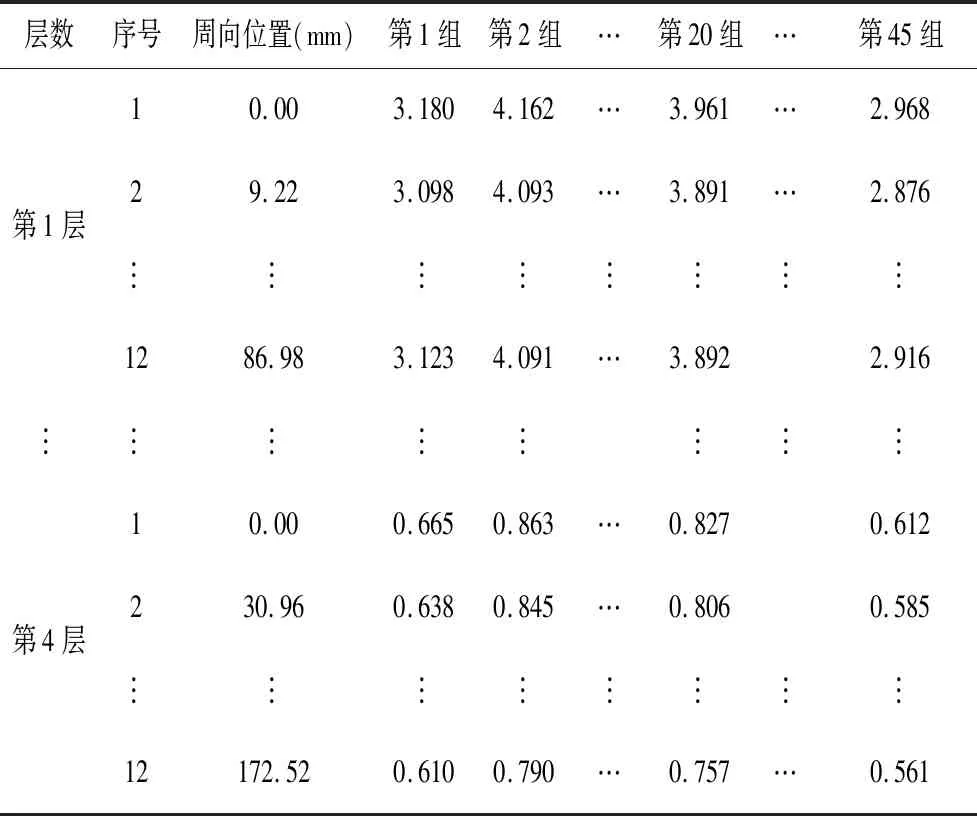
表2 不同心肌组织参数对应的左心室径向位移(t=0.4 s)Table 2 Radial displacements at the LV from different myocardial tissue parameters (at t=0.4 s)
4.2.2隐含层和激活函数 隐含层的选择根据经验和多次实验来确定,本研究中输入单元数为48,输出单元数为2,根据经验公式计算隐含层单元数的范围为[7, 18],再通过BP神经算法训练样本,综合考虑收敛时的误差和迭代次数,确定最佳的隐含层单元数为15。
输入层和隐含层的激活函数使用双曲型正切tansig函数,输出层使用purelin线性函数,训练函数用负梯度下降动量BP算法。接下来,使用Matlab软件编制BP神经网络程序并运行,得到心肌参数反演的BP神经网络结构,见图9。
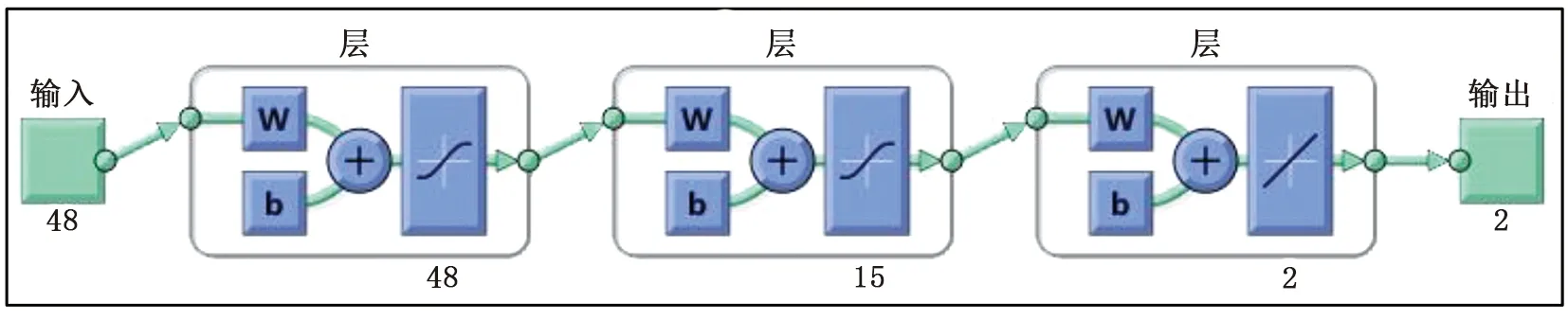
图9 Matlab中建立的BP神经网络结构Fig.9 BP neural network model developed via Matlab software
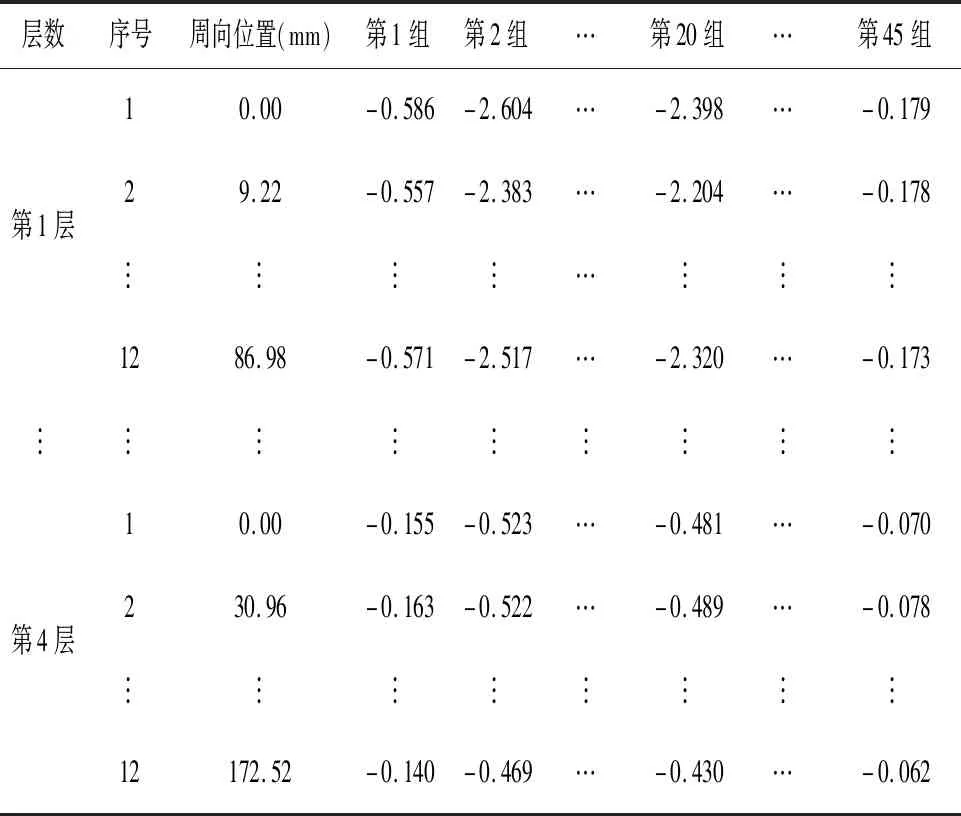
表3 不同心肌组织参数对应的左心室径向位移(t=0.6 s)Table 3 Radial displacements at the LV from different myocardial tissue parameters (at t=0.6 s)
4.3 心肌参数反演结果及讨论
临床上通过左心室标记点方法可获得心肌在不同位置点的径向位移。因此,为验证本研究方法,假定心肌组织性能参数为已知,据此通过有限元分析,获得左心室结构的响应数据,再通过BP神经网络对响应数据的反演,获得心肌组织参数的大小,并与假定的心肌组织参数进行误差比较。通过对4个假定实例的心肌组织参数反演得到在3个特征时刻下的反演参数的平均值,反演参数的平均值与真实值间的误差见表4。
由表4可以看出,4个实例的反演值平均值与真实值间的误差在3.58%以内,整体L2范数相对误差为0.72%,与临床医学诊断过程中的常见误差[21]相比,本研究参数反演的精度较高,可适合临床诊断的要求,同时说明本研究建立的BP神经网络具有高可靠性。
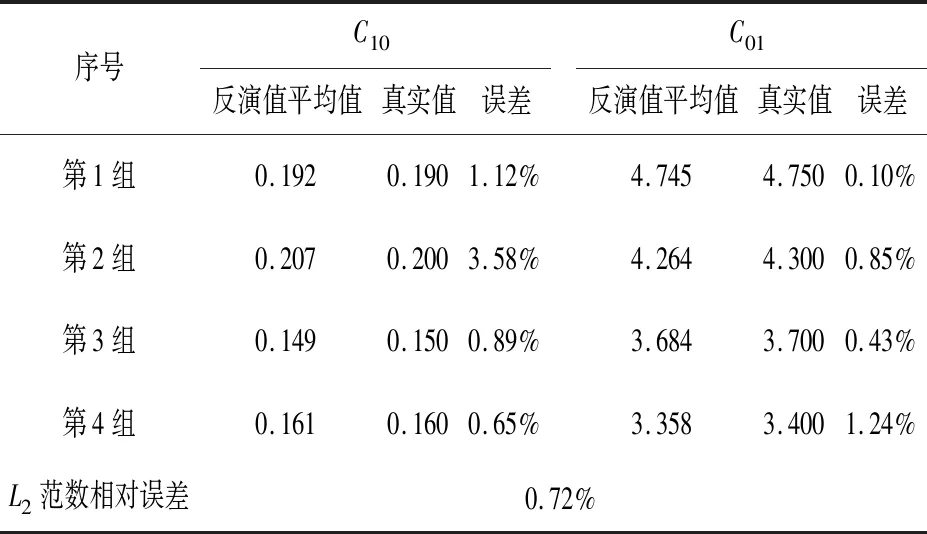
表4 真实心肌组织参数和反演心肌组织参数对比Table 4 The inversed results and their errors
5 结论
基于临床CT图像,建立了左心室的真实三维几何模型;根据左心室的动态有限元分析结果,提出了基于BP神经网络的左心室心肌组织参数的反演方法,获得了心肌组织Mooney-Rivlin超弹性模型下的心肌组织参数,反演值平均值与真实值具有很好的一致性,证明了本研究心肌组织参数反演方法的正确性,可为人体心肌组织性能的准确获得提供一种有效方法。
采用临床上获得的心脏患者左心室标记点变形数据,将此输入到本研究训练好的BP神经网络,反演得到心肌组织参数,可作为临床心脏疾病诊断的依据。本研究BP神经网络算法为左心室表象和心肌组织本征特性之间建立了定量关系,可定量描述心脏的健康程度,从而为临床心脏疾病的高效高精确诊断提供了一条可行途径。
