基于NSGA-Ⅱ的冷源机房设备运行参数多目标优化

2021-04-13闫军威卢泽东

科学技术与工程 2021年7期

闫军威，卢泽东，周璇

(华南理工大学机械与汽车工程学院，广州 510640)

中央空调系统是建筑内部的耗能大户，其能耗占比超过50%[1]。整个中央空调系统能耗来源主要由3部分组成：主机能耗、输送能耗、末端能耗，其中末端能耗约占空调能耗的15%[2]。而中央空调冷源机房设备包含冷水主机、冷冻泵和冷却泵，因此，冷源机房设备能耗占到中央空调系统总能耗一半以上。在实际工程中，高效运行的冷源机房一直是空调节能研究领域关注的重点，同时冷源机房运行参数优化也是研究人员和工程技术人员关注的热点问题。

随着对中央空调节能优化的深入研究，优化系统参数已经成为提高空调系统性能和空调节能量的有效手段。文献[3]针对现有的热舒适性控制方法存在的不足，采用复合形法求得满足热舒适条件下的空调能耗值最小时的最优组合参数，适用于夏热冬冷地区办公建筑空调系统的实时节能舒适控制。文献[4]通过建立空调系统能耗模型，运用蚁群算法对总能耗最小进行寻优，经过运行测试后的结果表明，优化后的节能率平均达到22.3%。文献[5]为实现风量水量最优组合优化，设定风机和冷冻泵的总能耗最小为目标函数，利用遗传算法对模型求解，与常规运行策略相比，得到的优化设定值的节能率达到13.38%。文献[6]为了提高汽车暖通空调系统(heating,ventilating and air conditioning,HVAC)系统的性能，通过遗传算法选择四通百叶窗式冷凝器进行多目标优化，以冷凝器的传热速率最大和冷凝器压降最小为双目标来优化冷凝器性能，结果表明，与初始冷凝器状态相比，最佳冷凝器的传热速率提高4%，压降降低8%。Nasruddin等[7]以表征热舒适度的指标——不满意百分比的预测数(predicted percentage of dissatisfied，PPD)和最小年度能耗为优化目标函数，利用人工神经网络并结合多目标遗传算法结合来优化HVAC系统，最后得到的优化效果明显，为研究复杂的中央空调优化问题提供了参考；文献[8]运用两种多目标优化算法对中央空调系统进行优化，将能效比和制冷量设置为双目标，并与单目标优化进行比较，得到不同的多目标优化方法在运算上各具优势的结论，其中，MO-DNS-PSO算法的运行效率更高，DNS-PSO算法的收敛性更好。

现有的参数优化研究中，通常是将能耗或能效视为唯一目标函数来进行优化研究，但这种优化方式具有一定局限性。空调系统运行参数的多目标优化研究大多集中在汽车空调领域，现有的中央空调多目标优化研究尚缺少对系统运行性能的量化研究。中央空调冷源机房设备数量众多，运行工况复杂且运行参数繁多，各参数之间耦合作用较强。在空调系统运行时，冷水主机运行参数和冷冻侧、冷却侧的运行参数相互耦合，冷水机组处于较大制冷量运行时往往难以保证系统总能耗水平较低，因此，空调系统参数优化可作为复杂的多目标优化问题进行求解。

多目标优化算法现已成为求解复杂的多元非线性问题的必要方法。常用的多目标进化算法主要有粒子群算法、模拟退火算法、非支配排序算法、差分进化算法等。其中，非支配排序遗传算法Ⅱ(non-dominated sorting genetic algorithm Ⅱ，NSGA-Ⅱ)具有较强的变量处理能力，能够最大限度地保持各优化目标之间的独立性和较好地全局寻优能力[9]。该算法由于具有运行速度快、解集收敛性好的优点，已经被广泛应用于众多研究领域。

针对上述问题，现提出一种基于NSGA-Ⅱ算法的冷源机房设备系统运行参数的多目标优化方法，以广州某商场建筑的空调冷源机房系统为研究对象，验证NSGA-Ⅱ算法在冷源设备系统运行参数优化的适用性和有效性。

1 方法及原理

1.1 多目标优化方法

所提出的多目标优化方法适用于空调冷源机房设备系统，流程框架如图1所示，步骤如下。

图1 冷源机房设备系统的多目标优化框架Fig.1 Multi-objective optimization framework of cold source equipment room equipment system

步骤一数据预处理：对采集的空调系统大量历史运行数据进行数据清洗，得到有效数据。

步骤二工况划分：在数据预处理的基础上，采用等宽离散化划分运行模式，再利用K-means聚类算法划分出运行工况。

步骤三影响因子分析：分析目标函数与影响因子间的相关性，进而确定决策变量。

步骤四多目标优化模型建立：确定模型的目标函数、决策变量以及约束条件，建立多目标优化数学模型。

步骤五利用NSGA-Ⅱ算法对模型实施优化，得到Pareto最优解集。

1.2 多目标优化问题

多目标优化问题是需要考虑多个目标满足某种条件下的最优化问题，最早由法国经济学家V. Pareto在1896年提出。随后，众多学者不断地探究多目标优化问题，多目标优化已成为许多领域的重要研究方向。多目标优化问题通常可描述为

(1)

式(1)中：x为决策变量。

1.3 Pareto前沿

Pareto前沿指的是所有非支配解的集合。

非支配解指的是假设S1、S2是多目标优化中的两个解，对于所有目标而言，若S1均优于S2，则称S1支配S2；若S1的解没有被其他解所支配，则S1称为非支配解(Pareto解)。

针对多目标优化问题，最终期望得到Pareto前沿，当有两个优化目标时，得到的Pareto前沿是一条曲线，两个以上目标时的Pareto前沿是一个超曲面。Pareto前沿上的所有解均不受其之外的解所支配。因此，Pareto前沿可为多目标优化问题提供一系列较优的解点。

1.4 NSGA-Ⅱ算法

NSGA-Ⅱ算法采用非支配排序，可以快速得到种群分布均匀的非劣最优解，具有很强的稳定性和适应性[10]。最初，Srinivas 等[11]提出NSGA算法，需要在选择算子执行之前对个体之间的支配关系进行分层，使得该算法计算复杂度较高且难以确定共享半径。文献[12-13]提出NSGA-Ⅱ算法，该算法引入了精英策略，应用快速非支配排序降低了复杂度，并且使用拥挤度比较算子，合并父代种群跟子代种群，使得下一代的种群从双倍的空间中进行选取，保留了种群中的优秀个体。该算法较以往多目标优化算法在应用上更具有广泛性和优越性。

为满足制冷量与系统总能耗作为双目标函数来优化系统运行参数，采用经典的多目标优化算法NSGA-Ⅱ寻求模型的最优解集，获得各工况的最优运行参数，进而分析各工况下的能效优化情况。NSGA-Ⅱ多目标优化算法流程图如图2所示，具体步骤如下。

图2 NSGA-Ⅱ多目标优化算法流程Fig.2 Multi-objective optimization algorithm of NSGA-Ⅱ

步骤一随机产生规模为N的初始种群。

步骤三从第二代开始，将父代种群与子代种群合并，进行快速非支配排序。

步骤四对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群；

步骤五达到满足程序结束的条件后，算法终止，否则，返回步骤二。

2 案例分析

2.1 研究对象

将广州市某商场建筑的中央空调冷源机房系统作为研究对象，该系统包含4台离心式冷水机组、6台冷冻水泵和6台冷却水泵设备，具体参数如表1所示。该单位冷源机房安装有自动控制系统及数据采集系统，采集冷源机房设备的运行参数存储在数据库中，包括冷冻水流量、冷冻水供回水温度、冷凝出水压力、冷凝回水压力、冷却水供回水温度、冷却水流量等，共计18维运行参数。

表1 制冷机房具体设备参数Table 1 Parameters of specific equipment in refrigeration equipment room

采用该商场2018年1—12月共计一年的历史数据。根据实际现场运行情况得知，该商场在较多时间处于单台主机运行状态。为保证算法优化的有效性，仅考虑2台小机单独运行时的工况。经过数据统计分析，其运行数据量共计27 506条。

2.2 数据处理

2.2.1 数据预处理

数据处理是将数据能够成功拟合模型和实施优化的重要前提，根据对数据的要求，需要对数据进行预处理。为拟合各工况模型，首先对原数据库中数据进行属性规约，最终得到制冷量、冷冻水流量、冷冻出水温度、冷冻回水温度、冷却水流量、冷却水出水温度、冷却回水温度、主机功率、水泵功率及频率共10维属性参数。由于数据在传输过程中可能出现错误以及设备运行出现的可能故障，处于刚开关机阶段的数据以及出现极限值数据属于异常数据，应将其剔除；剔除缺失值和异常值后，在Python上采用拉依达准则对各项数据进行统计计算，剔除较大偏差数据；最终得到有效数据共计 17 380 条。数据预处理流程如图3所示。

在这社会动荡时期，陶渊明去践行了他的“平生之志”，十三年间先后五次做官。十三年，不管他所任官职大小，还是几仕几处，都是他为实现“大济苍生”的理想抱负而不断尝试、不断失望终至绝望的行动体现。所以，陶渊明并不是没有出仕的志向，而是混乱的现实让他没有实现志向的机会，所以他最后一次为官，做了80多天的彭泽县令，以“寻程氏妹丧于武昌，情在骏奔，自免去职”的理由，在序言中写道：“尝从人事，皆口腹自役。于是怅然慷慨，深愧平生之志。”在这样的遗憾中结束了他的“兼济天下”的“平生之志”，留下的是不能有所作为的深深的惭愧。所以，东晋这一动荡的时代，造就了陶渊明的“平生之志”，也用现实毁灭了他的“平生之志”。

图3 数据预处理流程Fig.3 Data preprocessing

2.3 影响因子分析

冷源机房设备系统能效受到负荷率、冷冻水流量、冷冻出水温度、冷冻回水温度、冷却水流量、冷却水回水温度等影响，并且各参数间耦合性较强。为了研究各参数对系统能效的影响程度，在完成数据预处理的基础上，分析系统能效与影响因素间相关性，以此为多目标模型中决策变量的选取依据。本研究选取适用于描述两变量之间线性相关的皮尔逊(Pearson)相关系数，其定义是两变量的协方差与标准差的比，公式表示为

(2)

式(2)中:cov(X,Y)为随机变量X与Y的协方差;σX与σY分别为X与Y的标准差;ρX,Y介于-1～1。

系统能效与影响因子间的Pearson相关系数如表2所示。可以看出，对冷源机房设备系统能效产生影响的因素从大到小依次是：负荷率、冷冻水流量、冷却回水温度、冷冻回水温度、冷却水流量、冷冻出水温度和冷却出水温度。研究需要建立系统能耗和制冷量的双目标数学模型，结合影响因子相关性系数分析结果，选取相关性系数较大的冷冻水流量、冷却回水温度、冷冻回水温度、冷却水流量和冷冻出水温度共5个参数作为模型的决策变量，进而建立多目标优化的目标函数。

表2 系统能效与影响因子间的Pearson相关系数Table 2 Pearson correlation coefficient between energy efficiency and impact factor on air-conditioning system

2.4 运行模式及工况划分

根据上述影响因子分析结果，在中央空调冷源机房系统中，负荷率是能直接反映系统运行状态的重要指标。为充分反映中央空调冷源机房设备系统能效受到内外因素的影响，首先利用等宽离散化将负荷率划为4个等宽区间运行模式，剔除在负荷率60%以下的不稳定工况数据；再利用K-means聚类算法在4种运行模式下对室外环境温度和室外环境湿度两个参数进行聚类分析。

K-means聚类算法是一种无监督的机器学习算法，它需选取k个初始聚类中心Ci(1≤i≤k)，然后通过迭代计算原理得到样本中各簇的相似度，其相似度是通过欧氏距离进行计算，数学表达式如式(3)。确定最佳聚类数目k是该算法的难点，采用样本聚类误差平方和(sum of squared error，SSE)来判定最佳k。在每次聚类后计算SSE，随着聚类迭代，SSE会越来越小，最后会趋于稳定，变化过程的开始阶段下降率很大，当下降率首次变缓时的k被看作最佳的聚类数目。SSE表达式如式(4)所示。

(3)

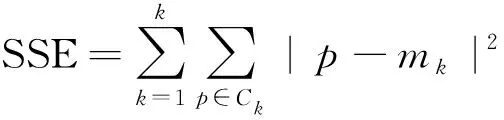
(4)

式中：x为数据对象；Ck为第k个聚类中心；n为数据对象尺寸；xj为x的第j个运行参数值；Ckj为Ck的第j个属性值；p为各簇中的运行参数值；mk为第k个簇的中心。

根据通过K-means聚类和误差平方和断定方法对4种运行模式下的运行数据进行聚类划分，从而得到系统的基本运行工况，运行模式及聚类划分情况如表3所示。共划分出32种基本运行工况，图4是32种基本运行工况的具体情况。

表3 运行模式划分及聚类情况Table 3 Classification of the operating mode and clustering result

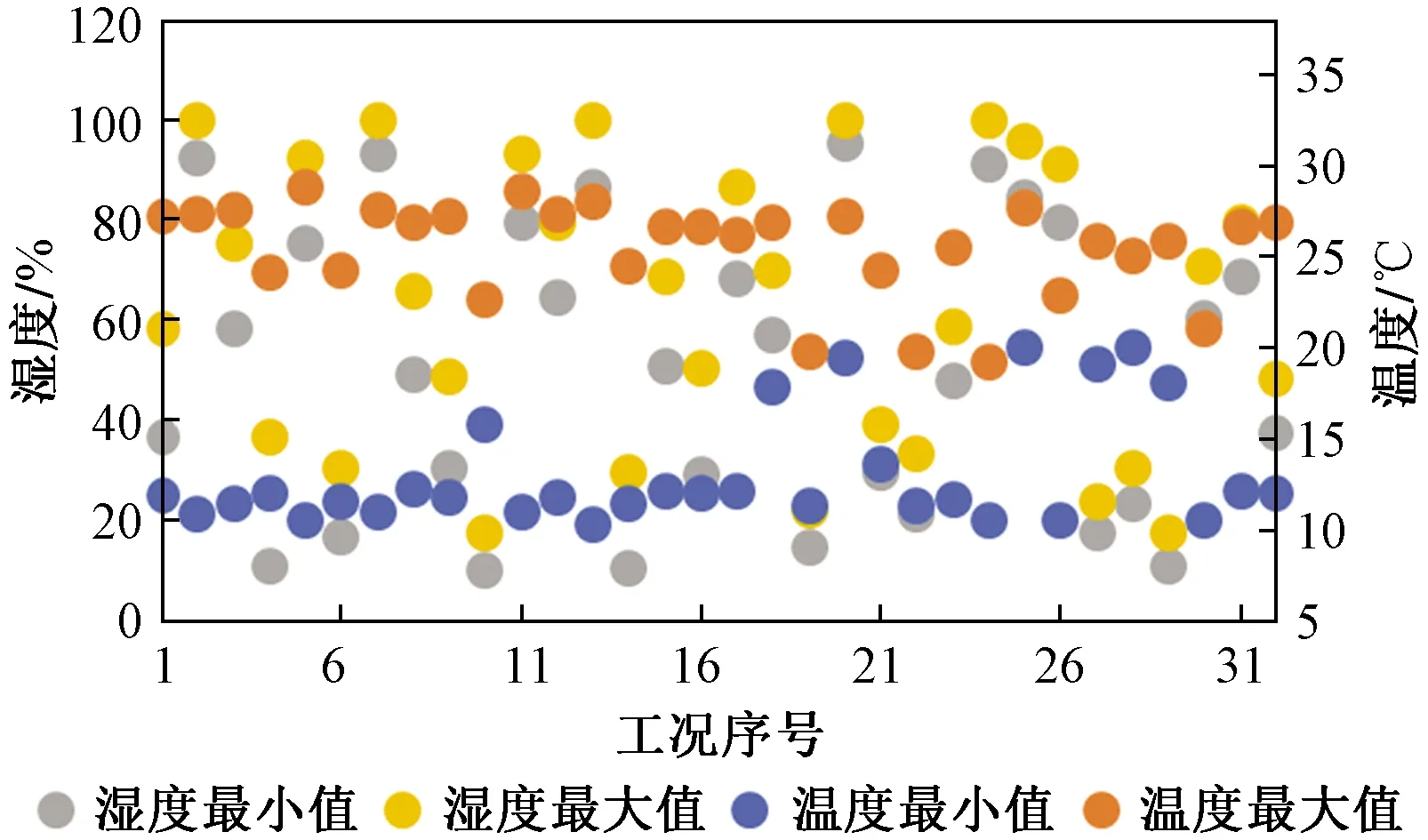
图4 32种基本运行工况Fig.4 32 kinds of condition of basic operation

2.5 冷源机房设备多目标优化模型建立

为深入挖掘空调系统的最优运行参数，实现中央空调冷源机房设备的高效运行，采用多目标优化研究方法优化运行参数。基于运行机理建立冷水主机、冷冻泵、冷却泵的能耗模型，进而确立目标函数。通常，中央空调系统运行参数的调节是通过在线控制系统完成的，控制系统能够设置冷冻出水温度、冷冻水流量、冷却水流量、冷冻水温差和冷却水温差等参数的目标值，控制系统通过调节电机频率和设备运行台数来间接调节冷冻回水温度和冷却回水温度，因此，通过优化得到的最佳运行参数对提高空调运行能效具有指导意义。

故需要根据空调系统运行机理，建立冷源机房设备的多目标优化模型，包括系统总能耗模型和制冷量函数表达式。

2.5.1 冷水主机能耗模型

空调冷水机组的建模方式主要分为理论模型和经验模型。现采用经验模型，经验模型是在研究冷水机组热力学特性的理论基础上，分析其与运行参数间的关系，从而建立一种数学模型的模糊表达形式。根据ASHRAE handbook推荐，将冷水机组的能耗拟合为冷冻回水温度和冷却回水温度的函数，采用两个二次多项式乘积的形式[14]。具体表达式为

(5)

2.5.2 冷冻水泵能耗模型

理论上，处于变频条件下的水泵性能参数遵循相似定律，但在实际运行中，其运行工况点并不完全遵循相似定律。根据在变频状态下得到的水泵实际运行数据，研究得出水泵功率与流量是二次多项式关系[15]。考虑到各工况数据量的不同可能影响模型拟合的准确性，因而将功率与流量的关系确立为三次非线性表达式，具体表达式为

(6)

式(6)中：f2为冷冻水泵功率，kW；vcwh为冷冻水流量，m3/h；a0、a1、a2、a3为回归系数。

2.5.3 冷却水泵能耗模型

冷却水泵流量可以通过调节电机功率实现变频控制，冷却水泵功耗模型与冷冻水泵功耗模型类似，拟合为流量的三次表达式为

(7)

式(7)中：f3为冷却水泵功耗，kW；vcw为冷却水流量，m3/h；b0、b1、b2、b3为回归系数。

2.5.4 约束条件

建立有效的约束条件是实施有效优化的重要保障，在中央空调工程设计方案以及实际应用中，为保障系统性能以及空调运行的安全性，运行参数均有相应的数值控制范围。对于指定的冷源机房，根据中央空调机组厂商规定的标准状况下运行参数值并结合该中央空调控制系统中的实际运行参数设定范围，能够得到各设备运行参数范围。决策变量均是连续型变量，以各变量阈值为准，建立多目标优化模型的约束条件，具体描述如下：

Tcl,min

Tel,min

vcwh,min

vcw,min

Tchws,min

2.5.4 多目标优化模型

对于确定的冷源机房设备系统，其总能耗与制冷量呈正相关关系，但较低的系统总能耗不一定得到较高的系统能效。系统能效比是制冷量与系统总能耗之比，为了优化后得到最佳能效，将系统能耗的最小值和制冷量的最大值设定为多目标优化的目标函数，冷源机房设备系统总能耗包含主机能耗和水泵能耗。目标函数的具体表达形式为

fmin(Tcl,Tel,vcwh,vcw)=f1+f2+f3

(8)

Q=cvcwh(Tel-Tchws)

(9)

式中：Q为制冷量，kW；c为水的比热，J/(kg· ℃)；vcwh为冷冻水流量，m3/h；Tchws为冷冻出水温度，℃。

3 仿真实验

3.1 Pareto优化结果

基于运行模式和工况划分，统计一年中各种运行工况的有效数据量，选取4种运行模式下的数据量最大的工况作为典型运行工况来进行优化。采用最小二乘法将典型工况下的有效数据拟合多目标优化模型，再用NSGA-Ⅱ算法对模型进行优化。

多目标优化问题通常存在一个解集，这些解之间对于多个目标函数而言是无法比较优劣的，因为一个解改进一个目标函数的同时会削弱其他目标函数[16]。采用NSGA-Ⅱ算法优化系统模型，以最大制冷量和最小总能耗为优化目标函数。图5展示的是4种运行模式下的典型工况Pareto前沿图。根据多目标优化理论可知，Pareto前沿均可作为优化方案解。选取4种运行模式下能效最高的点作为最优解，如表4所示。

图5 4种运行模式下的典型工况Pareto前沿Fig.5 Pareto frontier of Typical conditions in four operating modes

表4 4种运行模式下典型工况的Pareto最优解Table 4 Pareto optimal solutions under typical conditions in four operating modes

3.2 优化结果对比分析

在以往的空调优化研究中，广泛采用以空调系统能耗最低为目标函数的单目标优化方式来达到系统节能和能效提升的目的。文献[17]建立以系统总能耗最小为目标并运用遗传算法优化中央空调系统的运行参数，结果表明空调系统的节能率跟其部分负荷率有关，实际运行负荷越小，其节能空间越大。

将NSGA-Ⅱ算法的多目标优化方法与经典遗传算法优化方法在相同工况下对冷源机房设备能效优化的效果进行比较。将建立的能耗模型作为唯一目标函数，采用经典遗传算法对模型进行优化。运用单目标算法进行优化时，设置初始种群为100、交叉概率为0.7、最大进化代数为300。4种典型运行工况的单目标优化结果如表5所示。

表5 4种典型工况的经典遗传算法单目标优化结果Table 5 Single-objective optimization results of the classic genetic algorithm under four typical conditions

图6所示为两种优化方式在不同工况下的平均循环性能系数(coefficient of performance，COP)对比情况，COP表达式如式(10)所示。从图6可以看出，在提升系统运行能效方面，4种典型工况下的多目标优化方法相对于普通优化方法更具有优势。

图6 4种典型工况下的两种优化方式COP比较Fig.6 Comparison of COP values of two optimization under four typical conditions

(10)

3.3 仿真验证

最后，为验证本文方法的实际参考价值，将4种运行模式下的典型工况进行优化前后对比分析，为更直观地体现对比效果，在Pareto前沿上选取与优化前制冷量相同的优化解点，再进行比较验证。如图7所示为4种典型工况优化前后的能耗及能效的比较。

图7 典型工况下多目标优化前后系统能耗、能效比较Fig.7 Comparison of energy consumption and energy efficiency on the air-conditioning system before and after multi-objective optimization under typical conditions

优化结果表明，4种典型工况经过多目标优化后，能效随着制冷量的增大而持续增大，相对于实际运行工况，优化后有更稳定的运行参数。相较于系统原有运行方式，优化后的运行参数能明显提高其运行能效，经过计算，多目标优化后系统能效平均提升14.35%，能耗平均降低12.52%。