钢管-纤维增强水泥基复合材料混凝土叠合柱轴压性能
2021-04-13车佳玲杨淑雁林加胜
陈 港, 包 超*, 车佳玲, 杨淑雁, 林加胜
(1.宁夏大学土木与水利工程学院, 银川 750021; 2.马来西亚彭亨大学工程学院, 关丹 26300)
钢管混凝土叠合柱是由核心钢管混凝土与外围钢筋混凝土共同作用的一种新型组合结构,具有承载力高、延性好、耐火性能强等优点,在高层建筑建设中被广泛应用[1-2]。近年来,中外学者对于钢管混凝土叠合柱的静力学性能展开了大量试验和理论数值的研究[3-6],研究发现钢管混凝土叠合柱的承载力不仅与混凝土强度、钢材强度有关,配箍特征值、纵筋率以及叠合比等参数也会对其产生影响,通过改变参数大小可以有效提高钢管混凝土叠合柱的承载能力。
尽管钢管混凝土叠合柱具有较好的承载能力,但由于钢材与普通混凝土之间力学性能的巨大差异,导致长期服役过程中外包混凝土容易开裂,进而造成内置钢管耐久性损伤和性能退化等问题。为改善钢管混凝土叠合柱中钢管与填充材料和外包材料之间的相互作用关系,有学者提出将高延性纤维增强水泥基复合材料(engineered cementitious composite,ECC)引入钢管混凝土叠合柱,用以替代普通混凝土。ECC材料[7-9]是一种超高延性的新型建筑材料,与普通混凝土具有类似的抗拉性能与抗压性能,但ECC具有更强的拉伸性能[8]。已有研究成果大都将ECC材料应用于包括梁[10]、柱[11-13]、框架节点构件[14]或整体结构修复[15]。关于钢管-ECC混凝土叠合柱力学性能的研究主要集中于长细比小于4的短柱,然而对于实际工程中普遍存在的长柱力学性能的关注相对较少,为此,现采用数值模拟方法对钢管-ECC混凝土叠合柱的轴压性能进行研究,通过参数分析系统研究各因素对其承载力影响规律。
1 模型设计
共设计了4个普通钢管混凝土叠合柱和12个钢管-ECC混凝土叠合柱模型,包括圆截面、方形截面两种钢管类型,柱高分别为900、1 200、1 500 mm,用以对比构件长细比的影响,试件截面均为300 mm,如图1所示。

图1 叠合柱横截面示意图Fig.1 Cross section diagram of composite column
圆钢管外径为180 mm,为保证截面含钢率相同,取方钢管边长为160 mm;钢管强度均为Q345,屈服强度fy=345 MPa,泊松比取0.3,弹性模量206 GPa;纵筋和箍筋均采用HRB400级钢筋,箍筋间距分别为100、200、300 mm;普通混凝土强度等级为C30、C40;试件编号及其他具体参数如表1所示。
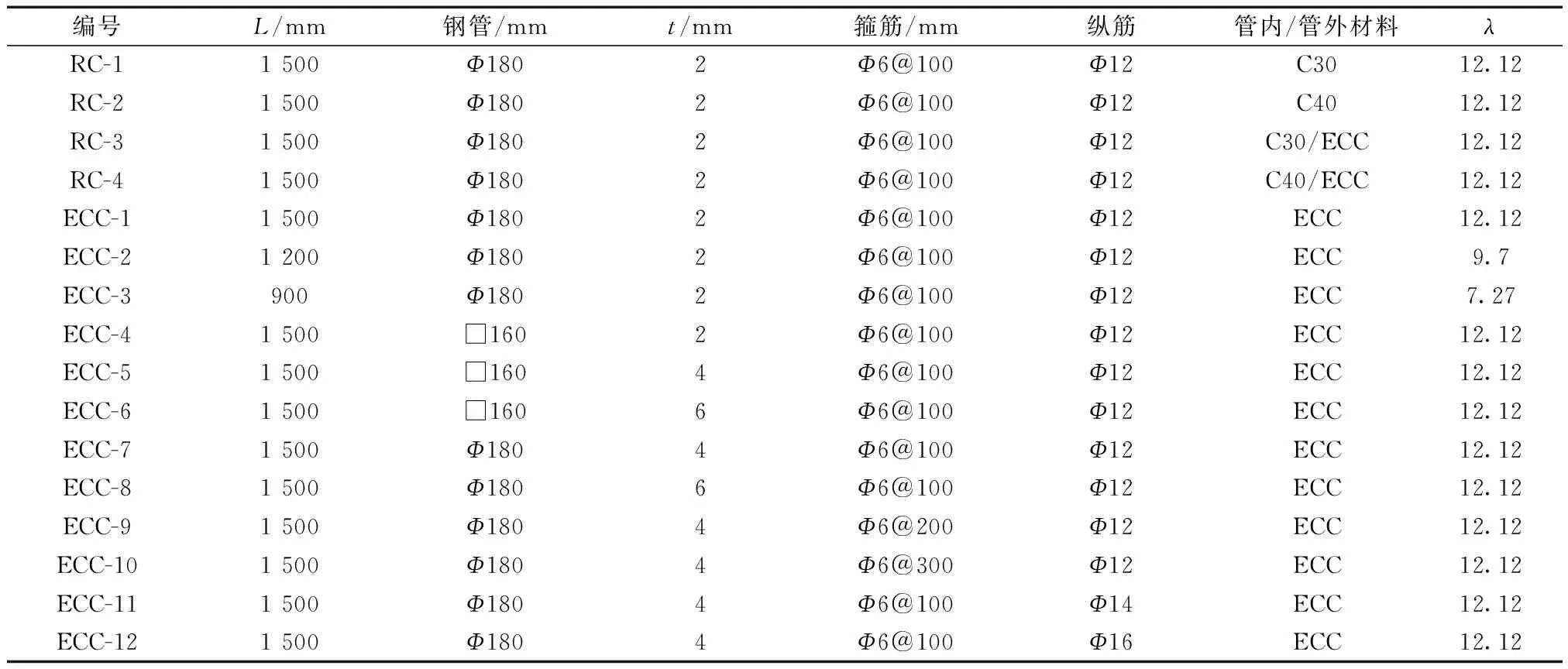
表1 试件编号及设计参数Table 1 Specimen number and Design parameters
2 模型建立与验证
2.1 有限元模型建立
钢材选用强度等级为Q345级低碳钢,其材料模型采用韩林海[5]提出的二次塑流本构,屈服准则服从Von Miss屈服准则。
混凝土以及ECC材料均选用ABAQUS中自带的混凝土损伤塑性模型,泊松比0.2,黏性系数0.005,膨胀角37°,屈服面形状参数K取0.667,偏心率取0.1,混凝土的双轴受压强度与单轴受压强度之比取1.16。为了考虑钢管的约束效应,混凝土材料采用韩林海提出的本构关系模型[5]。对于ECC材料,选用文献[9]中龄期90 d的试件实测应力-应变(σ-ε)曲线进行模拟,如图2所示。
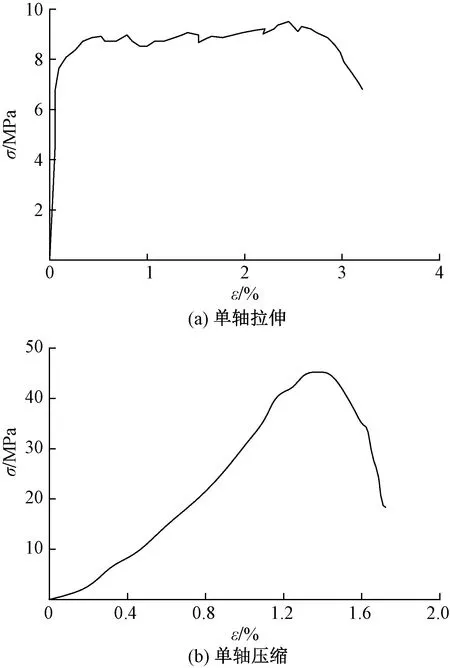
图2 ECC材料应力-应变(σ-ε)曲线Fig.2 ECC material stress-strain (σ-ε) curve
核心混凝土、钢管、钢筋骨架以及垫板均采用三维实体缩减积分单元C3D8R,纵向钢筋与箍筋采用三维桁架Truss单元;钢筋骨架采用Embedded形式,嵌入核心混凝土之中,钢管单元与混凝土、ECC单元之间为表面-表面(surface to surface)接触形式,法线方向采用“硬接触”,而切线方向则选用摩尔-库伦摩擦,罚摩擦因数取0.3。试件上下端部的垫板假定为弹性模量无穷大的刚体,垫板与核心混凝土、钢管之间采用“Tie”连接,试件的上端设为自由端,底部设置为固定端约束,X、Y、Z轴方向的位移以及转角为零,防止在加载过程中柱子出现平面外的位移。试件的加载制度则采用的位移加载的方式控制,在试件顶部施加荷载。
2.2 模型合理性验证
为了验证有限元模型的合理性,对文献[6]中的核心钢管混凝土叠合短柱轴压试验进行有限元分析,对其中的CSTRC1、CSTRC3试件进行数值模拟。如图3所示,有限元计算所得曲线与试验结果趋势一致,吻合性较好。

图3 有限元结果对比图Fig.3 Comparison of finite element results
数值模拟计算所得的极限荷载与试验结果对比如表2所示,二者误差仅为0.17、0.16,完全在可接受范围内。

表2 极限承载力对比Table 2 Comparison of ultimate bearing capacity
3 有限元计算结果
3.1 破坏模式
图4所示为不同叠合柱试件的应变云图,显示试件在峰值荷载下最大塑性应变结果,云图的颜色越接近红色表示该区域发生的破坏变形越大。如图4所示,试件 RC-1与ECC-1的破坏模式相同,应变从柱中截面向两侧发展,破坏程度逐渐加大,其次边角部分的混凝土被压碎;峰值荷载下RC-1、ECC-1的最大塑性应变分别为2.284×10-3和4.172×10-3,ECC-1约达到了前者的2倍,这是因为在ECC混凝土材料具有较好的拉伸性能,使得钢管-ECC混凝土叠合柱能承担更大的变形,说明采用ECC材料能有效改善钢管混凝土叠合柱的延性,从而提高试件的承载能力。
从图4(b)与图4(c)的应变云图对比发现,当钢管-ECC混凝土叠合柱的钢管壁厚增大时,ECC-7则是在柱中截面发生屈服破坏,试件在截面中部破坏最大,向两侧逐渐减小;最大塑性应变为4.666×10-3,相比ECC-1增加了12%。钢管厚度的增加意味着钢管-ECC混凝土叠合柱的刚度得到有效提高,增强了对核心混凝土的约束作用,从而提升了整体的承载力。为验证长细比对试件破坏模式的影响,将图4(a)与图4(c)的应变云图进行对比,可以看出长细比较小的ECC-3试件在柱中截面发生屈服,与ECC-7破坏模式一致。从图4中发现在柱边没有箍筋的部位出现了较大的应变,这是由于外包混凝土没有箍筋的约束所造成的。
3.2 参数分析
3.2.1 ECC、混凝土材料
表3列举了16个模型的极限承载力,以RC-1为参考对象,可以看到采用ECC混凝土材料替代外包普通混凝土使得钢管混凝土叠合柱的极限承载力大幅增加,增加幅度达42%,同时可以发现配筋率、钢管截面类型与厚度等参数对试件承载力的影响较为显著。
图5为不同混凝土类型下钢管混凝土叠合柱的承载力-位移曲线图,从图5可以看出,钢管-ECC混凝土叠合柱的承载力、延性都普遍高于普通钢管混凝土叠合柱。

图5 不同混凝土类型下的承载力-位移曲线Fig.5 Bearing capacity displacement curves of different concrete types
当试件RC-1、RC-2达到极限荷载时,试件RC-3、RC-4的承载力还处于上升阶段并未达到峰值,屈服位移分别增加了73%、77%;同时RC-3、RC-4的极限承载力分别提高了42%与20%。当ECC混凝土同时替代核心、外包材料时,试件ECC-1的峰值荷载相对于RC-1则提高了大约59%,试件承载力与延性的提高主要得益于外包ECC混凝土较高的拉伸延性特征,在峰值荷载时还处于应变硬化阶段,能够继续承担荷载,此时的普通混凝土已发生了脆性破坏,无法承载荷载,导致后期承载力下降,延性较差。其次,ECC混凝土的极限压应变及峰值应力下对应的应变均要大于普通混凝土,因此钢管-ECC混凝土叠合柱的承载力力与延性比普通钢管混凝土叠合柱强。
3.2.2 构件长细比
图6为不同长细比下钢管-ECC混凝土叠合柱的荷载-位移曲线,从图6可以看到,在其他参数相同的条件下,钢管-ECC混凝土叠合柱极限承载力随着长细比的增大而减小,在达到屈服位移之前,随着长细比的增加,试件的承载力-位移曲线随着长细比的增加而逐渐变得平缓,屈服位移逐渐后移,从2.925 mm延长至5.189 mm,构件长细比的增加在一定程度上改善的钢管-ECC混凝土叠合柱的延性。长细比为7.27、9.7、12.12的钢管-ECC混凝土叠合柱,其极限承载力分别为4.691、4.652、4.622 kN,随着长细比的增加,峰值荷载分别降低了0.8%和1.5%,可以看出构件长细比的增加对钢管-ECC混凝土叠合柱极限承载力的影响并不显著。

图6 不同长细比下的荷载-位移曲线Fig.6 Bearing capacity-displacement curves under different slenderness ratios
3.2.3 钢管截面形式与壁厚
图7为不同钢管壁厚度下钢管-ECC混凝土叠合柱的荷载-位移曲线,从图7可以看到,从试件加载到破坏过程中,采用圆截面和方截面钢管的钢管-ECC混凝土叠合柱的承载力与刚度均随钢管厚度的增加而逐渐增大,在极限荷载以后,随着钢管厚度的增加,试件的延性得到大幅提高。如表3所示,钢管厚度为2、4、6 mm时,试件ECC-1、ECC-7与ECC-8的极限承载力分别为4 622.43、4 967.34、5 314.31 kN,承载力分别提高了7.5%与15%,而采用了方截面钢管类型的试件ECC-4、ECC-5和ECC-6的极限承载力分别为4 542.10、4 943.87、5 307.07 kN,极限荷载分别增长了8.8%和17.0%,与圆截面钢管类型的试件增长幅度基本一致,与构件长细比的影响相比,增加钢管厚度能更好地提高试件承载能力。

图7 不同钢管厚度下的荷载-位移曲线Fig.7 Bearing capacity displacement curve of different steel pipe thickness
如图8所示,在钢管厚度相同的情况下,圆钢管-ECC混凝土叠合柱的承载力要强于方钢管-ECC混凝土叠合柱。钢管厚度为2 mm时,采用圆截面钢管的钢管-ECC混凝土叠合柱与采用方截面钢管的钢管-ECC混凝土叠合柱极限承载力差距最为明显,两者差距约为1.8%;随着钢管厚度的增加,两者之间的差距逐渐减小;当钢管厚度达到6 mm时,两者的极限承载力差距仅为0.1%。这是由于圆钢管对于核心ECC混凝土的约束作用更强,而方形截面钢管在加载过程中其边角部位容易出现应力集中,导致了试件的承载能力有所减弱;当钢管厚度达到一定程度时,钢管截面形式的改变所造成的影响可不用考虑。除此之外,从图8可以看到,试件的极限承载力与钢管厚度近似呈正相关。

图8 不同钢管截面、壁厚下的极限承载力Fig.8 Bearing capacity displacement curves of different steel pipe sections and wall thicknesses
3.2.4 配筋率与配箍率
图9为不同纵筋直径下钢管-ECC混凝土叠合柱的承载力变化情况,从图9(a)可以看出,在加载过程中,钢管-ECC混凝土叠合柱的极限荷载与刚度随着纵筋直径的增大而增大,极限荷载之后试件的延性也随着纵筋直径的增大而提高,当纵筋直径从12 mm增加到14 mm时,钢管-ECC混凝土叠合柱的极限荷载提高了3.7%,纵筋直径从12 mm增加到16 mm时,极限荷载提高了8.8%,所以适当提高纵筋直径可以有效提高试件的承载力和延性。
不同箍筋间距下钢管-ECC混凝土叠合柱的荷载-位移曲线如图9(b)所示,试件在达到极限荷载前,3条曲线的荷载位移曲线基本重合,当箍筋间距从100 mm增加到300 mm时,峰值荷载分别下降了1.0%、1.5%,随着箍筋间距的增加,钢管-ECC混凝土叠合柱的极限荷载呈减小的趋势,与改变纵筋直径的方法相比效果并不明显。
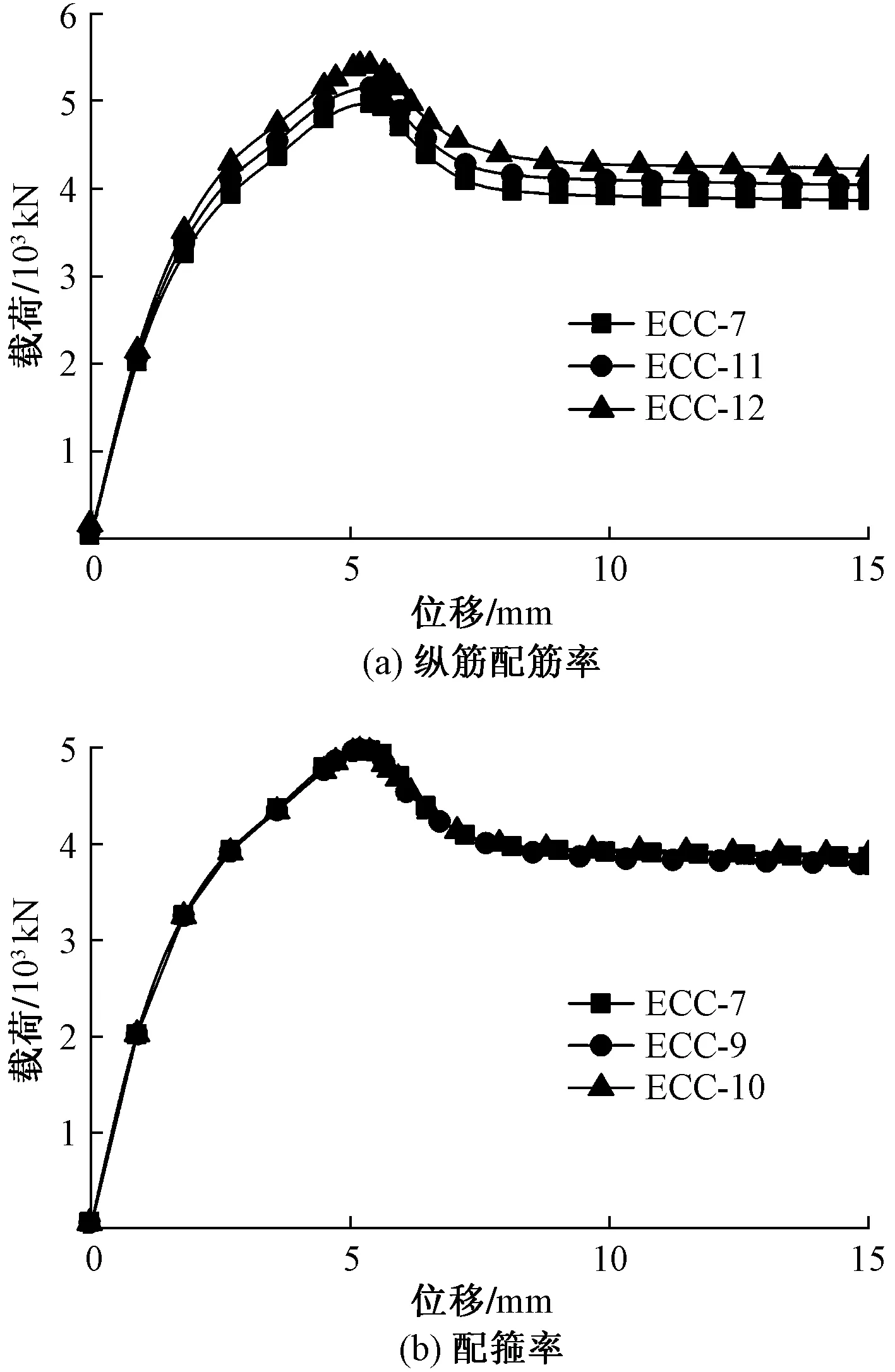
图9 不同纵筋配筋率、配箍率下荷载-位移曲线Fig.9 Bearing capacity-displacement curve of different longitudinal reinforcement ratio and stirrup ratio
4 结论
采用数值模拟方法研究了各参数对钢管-ECC混凝土叠合柱轴压承载力的影响规律,得出以下结论。
(1)外包ECC混凝土对钢管混凝土叠合柱承载力的提高有非常显著的作用,以本文模型为例,采用ECC混凝土替代普通外包混凝土能使钢管混凝土叠合柱的承载能力提高可达42%;钢管-ECC混凝土叠合柱延性较普通钢管混凝土叠合柱也得到显著加强。
(2)钢管-ECC混凝土叠合柱的承载能力随着长细比的增加而降低,但构件变形能力却随着长细比的增大得到提升。
(3)钢管厚度是影响钢管-ECC混凝土叠合柱承载力大小的重要因素,通过增加钢管厚度能有效增强试件的刚度与极限承载力;在截面含钢率相同条件下,圆截面钢管的约束能力强于方形截面钢管。
(4)外包纵筋的直径与箍筋间距对钢管-ECC混凝土叠合柱承载能力同样具有提高作用,但箍筋间距变化对承载能力提升效果相对较小,故不建议选用过小的箍筋间距。
