抗环境光照影响的边坡变形摄像监测方法
2021-04-13王寿旭马沁巍郭海旭邢同振
王寿旭, 马沁巍*, 郭海旭, 邢同振
(1.北京理工大学宇航学院, 北京 100081; 2.中国矿业大学(北京)力学与建筑工程学院, 北京 100083)
边坡是指自然或人工形成的具有一定坡度的坡面,是人类工程活动中最基本的地质环境之一,也是工程建设中最常见的工程形式[1]。边坡上的土体或者岩体,受河流冲刷、地下水活动、雨水浸泡、地震及人工切坡等因素的影响,在重力作用下,沿着一定的软弱面整体地或者分散地顺坡向下滑动的现象称为滑坡。滑坡是一种极具破坏性的地质灾害,据统计在中国地质灾害发生比例中占50%以上[2],造成了重大的财产损失和人员伤亡,因此滑坡灾害防治刻不容缓。对滑坡灾害进行预防虽可以使用人工到现场观测的方式,但是需要耗费大量成本,仅能够用于高速公路、隧道桥梁等重要工程,对于中国众多的边坡而言远远不够。因此,通过传感手段,对边坡的变形进行实时监测并判断其状态是更为行之有效的手段。
目前,边坡变形监测方法主要分为接触式和非接触式两类:接触式测量的典型代表是仪器监测法和全球定位系统(global positioning system,GPS)监测法。仪器监测法是在边坡上打孔后埋入一定数量的电学传感器(如测斜仪[3]、位移计[4]等),测量出边坡位移、角度[5]、应力等参数,其优点是系统简单、成本低廉、测量精度较高,但是布设工作量大,量程有限,且一旦发生大位移,滑动仪器容易受损,无法开展二次测量;GPS监测法是在边坡上设置测站,测站通过接收卫星信号并分析获取自身的三维坐标,之后计算变形。该方法可以进行自动化、全天候连续监测,但是在实际测量中,定位结果受到卫星星历误差、接收机钟差等多重因素的影响[6-7],测量分辨率低。为解决此问题往往需要对长时间获取数据进行平均来压制噪声,时间分辨率不足。更为重要的是,以上两类方法均需要在危险的边坡上进行作业,在实际使用过程中受到很多的限制,因此研究者又开发出了多种非接触测量方法。非接触测量的典型代表是全站仪和边坡雷达。全站仪通过测角和测距综合计算获得边坡上特征点的三维坐标,测量精度较高但是只能进行单点测量[8-9]。边坡变形存在空间上的强非均匀性特征,因此更需要的是全场测量方法以获得边坡变形的全貌。边坡雷达使用电磁波对坡面进行扫描,获得干涉图像,分析相位变化获取边坡变形,覆盖范围广泛,可连续观测,但在坡体表面起伏较大或植被覆盖严重时容易出现相位失相关现象,且雷达信号在大气条件(温度、湿度、气压)影响下会产生相位差[10-12],使得测量精度严重下降。
近景摄影测量是利用图像采集设备远距离获取边坡图像,之后对图像进行处理和分析,识别和定位边坡图像中特征点坐标,进而计算变形的技术[13-14]。该方法不需要在坡面上布设传感器,维护成本低,能够实现全场测量,可准确定位危险位置,适用于各类型边坡的变形观测,是目前新兴的边坡变形监测技术。中外学者在此方面开展了广泛的研究和应用工作:如Ohnishi等[15]使用数字相机从各个方向拍摄的边坡图像,重建了边坡体的三维形貌,但其并未开展变形测量应用;Matori等[16]使用类似方法开展了历时330 d的野外观测,获得了边坡变形演化过程;Travelletti等[17]用数字相机观测了阿尔卑斯山脉某处边坡的变形,并首次指出环境光照变化是影响测量精度的最核心因素。事实上,在长期野外测量中会不可避免地遇到由于太阳照射方向发生改变而引起的光照变化的情况,进而影响图像的灰度一致性。而图像又是变形分析的唯一基础数据,图像灰度受到影响必然会导致分析精度的下降。Travelletti等虽然发现了光照变化会对测量精度造成影响的问题,但并未提出相应的解决方法。随着边坡变形监测从定性观察到定量监测需求的转变,对测量精度的要求不断提升,上述问题已经成为阻碍该方法进入大规模实际测量应用的主要障碍。因此迫切需要对环境光照引起的变形测量误差、对测量精度的影响规律和抗光照影响的变形分析算法开展深入系统的研究工作,这对开展土木交通等其他野外摄像测量应用同样具有重要意义。
现从环境光照的物理过程出发,研究光照变化引起的图像灰度变化机理,分析总结光照变化特征及其对图像灰度的影响规律,发展一种基于灰度梯度的强鲁棒性边坡图像变形分析算法,最后通过室内和野外实验验证该算法的有效性。
1 光照变化对传统算法精度的影响分析
基于图像的变形测量方法通过跟踪变形前后图像(分别称为参考图像和变形图像)中同一点的移动,来获得变形信息(图1),其关键在于精确匹配到参考图像与变形图像中对应点的位置。常用的匹配方法是基于灰度特征的匹配方法,该方法假设在变形过程中图像的灰度具有不变性(灰度不变假设)[18],以相关函数为度量,搜索变形前后图像中最相关的点。相关函数的一种常见定义方式[19]为
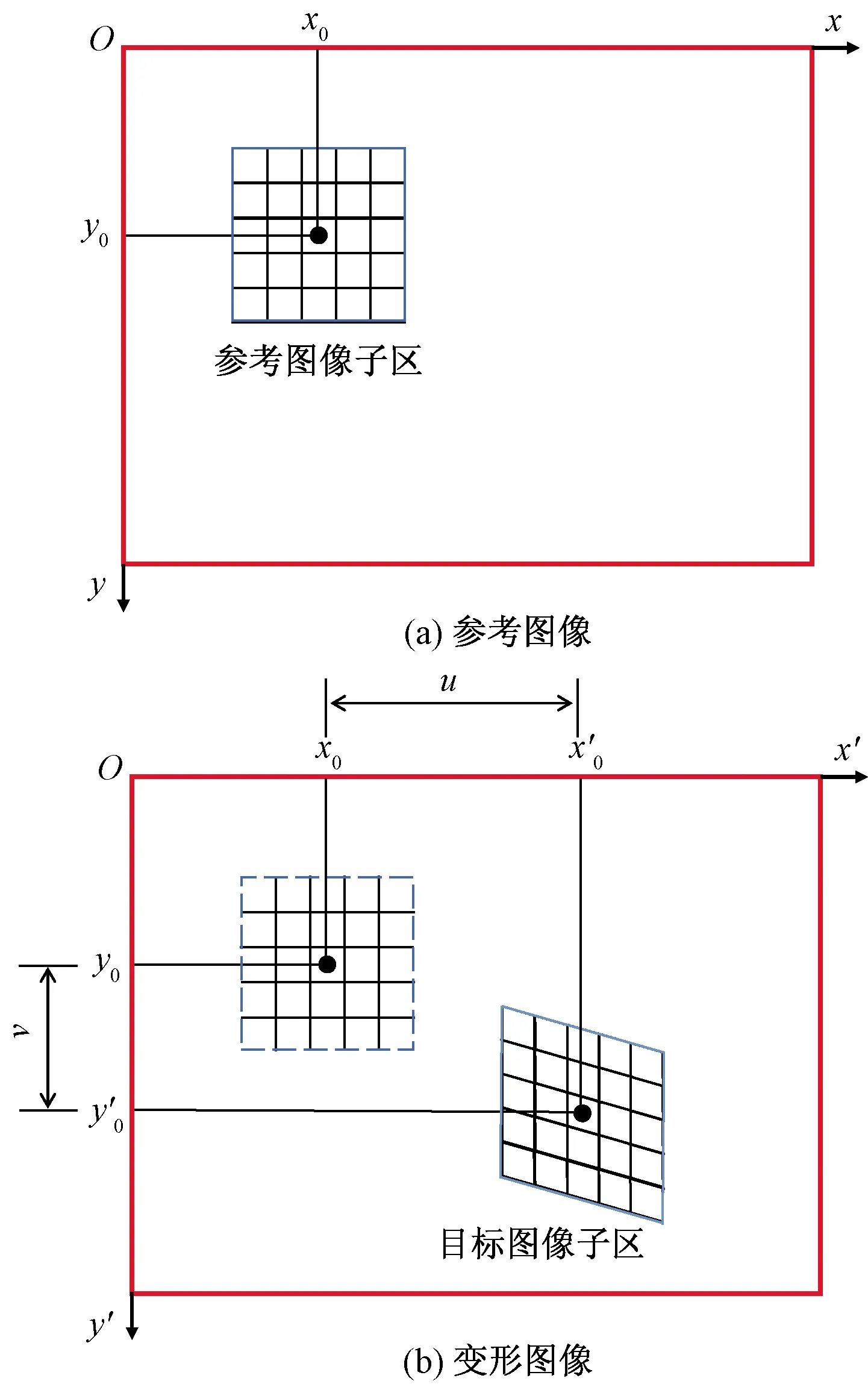
图1 图像变形分析原理示意图Fig.1 Schematic diagram of image deformation

(1)

然而在边坡监测中,受光照变化的影响,各个时刻的图像灰度将发生变化,导致灰度不变假设失效,造成图像失相关,引起变形分析误差。为了直观地展示光照变化对传统匹配方法变形分析精度的影响,本文对此过程进行了模拟。依据式(2)为图像施加一个灰度变换,模拟光照变化引起的散斑图灰度变化,结果如图2所示。

图2 散斑图对比Fig.2 Contrast of speckle patterns
fO=kfn(x,i)+G0,i=1,2,…,N
(2)
式(2)中:N为图像列数;fn(x,i)为原图灰度;fO(x,i)为调整后图像灰度。此处,k=0.003,G0=0.5。

表1 误差对比Table 1 The errors of contrast
从表1可以看出,光照变化会对变形分析精度产生较大的影响。观察相关函数分布的主峰顶点可以发现,当为图像施加光照影响后,主峰的位置会发生一定的偏移,从而造成定位发生误差,如图3所示。

图3 相关函数分布曲面Fig.3 Surface of correlation function distribution
在野外真实测量条件下,环境光照更加复杂,对灰度的影响更加剧烈,可能会对测量精度造成更加严重的影响。图4展示了野外同一天不同时刻拍摄到的图像,在此过程中,边坡并未发生变形。按照上述方法,将10:00的图像作为参考图像,将17:00的图像作为变形图像,计算二者间的相对变形量,按照理论位移为0像素,实测值与理论值的平均绝对误差和标准差如表2所示。

图4 野外真实边坡图像Fig.4 Slope image in the field

表2 误差对比Table 2 The errors of contrast
由表2结果可知,计算得到的两个方向的位移误差更大,原因在于光照的变化使得图像灰度匹配出现了失相关现象,而导致计算错误(图5)。综上分析可知,光照变化对灰度匹配的方法具有严重的影响,造成变形计算误差,因此,灰度特征并不适合作为边坡图像的匹配特征,需要选取一种新的抗光照变化的特征并发展相应的匹配算法,进而精确地计算出边坡的变形。

图5 相关函数分布曲面Fig.5 Surface of correlation function distribution
2 抗光照影响的变形分析方法
2.1 方法原理
通过第2节的分析可知,野外测量中所获得的边坡图像会被动叠加上一个光强场,导致图像灰度发生变化。设原图像灰度分布为I(x,y),由于边坡表面存在凹凸、裂隙等特征,材质纹理均不一样,因此拍摄到的图像灰度分布显示出随机性特征。当光照条件发生变化时,相当于在原来的灰度分布基础上增加另一个非线性变化,即灰度分布f(x,y),则光照变化后的灰度分布为I′(x,y)=I(x,y)+f(x,y)。
从信号角度上看,原图像I的灰度在空间上的分布相对于光照而言是一个高频信息,即光照后的图像I′实质上是在一个高频信号I上叠加了一个低频信号f(图6)。对一个小子区而言,相当于在原灰度分布上叠加了一个线性分布的光强变化,即一个线性信号。在此过程中,虽然灰度的绝对值发生了变化,但是其灰度梯度并未受到影响。因此,采用灰度梯度作为该子区的特征应该能够较好地消除光照的影响。

图6 光照对灰度分布影响示意Fig.6 Influence of illumination on gray distribution
利用高斯差函数提取出图像在频域空间中的高频信息,基于局部灰度梯度为每一个特征点分配一个主方向,并利用周围像素生成一个特征向量,使得该特征点具有唯一性,不随光照变化而变化,提高特征点的匹配率。
根据上述分析可知,消除光照影响算法的核心在于匹配时,不使用已经受到光照影响的灰度分布作为特征量,而使用对光照不敏感的灰度梯度分布作为特征量。因此,需要对子区的灰度进行变换。
设子区的灰度矩阵为I′,利用高斯卷积核对相邻尺度空间做差分建立高斯差分(difference of Gaussian,DoG)金字塔,检测局部极值作为整像素特征点[20-22]。DoG算子表示为
D(x,y,σ)=[G(x,y,kσ)-G(x,y,σ)]*I′(x,y)=
L(x,y,kσ)-L(x,y,σ)
(3)
(4)
式中:I′(x,y)为输入图像;σ为尺度空间因子;k为相邻尺度空间因子比例系数。
将金字塔中的每一个极值点与它的8个邻域值、对应的上一层尺度邻域值、下一层尺度邻域值(共26个值)进行比较,均大于或者均小于这26个值的极值点即为整像素极值坐标点,且检测到的特征点与尺度无关。
完成整像素特征点检测之后,先确定特征点的方向和特征描述符,进行整像素特征点匹配,最后确定特征点的亚像素坐标,从而提高特征点坐标的精度。具体方法如下:
(1)确定主方向。特征点的方向参数可由特征点的梯度大小m(x,y)和方向θ(x,y)表示,即
m(x,y)={[L(x+1,y)-L(x-1,y)]2+
[L(x,y+1)-L(x,y-1)]2}1/2
(5)
(6)
式中:L为输入图像的高斯卷积。
(2)建立特征点描述符。每个特征点具备3个信息:位置(x,y),尺度m和方向θ,通过向量建立一个描述符来表示特征点,使其具备尺度、光照和视角的不变性。该描述符包含对该特征点有贡献的周围像素点,因此具有独特性。
首先以特征点为中心,将邻域坐标轴旋转到主方向,使其具备旋转不变性;选取特征点周围1616的区域,并将此区域分为44的子区域,每个子区域内计算8个方向(0~360°划分为8个方向区间,每个区间45°)的梯度累加和,生成128(448)维特征向量。通过对特征点周围像素进行分块,生成具有独特性的向量,且该向量在该区域图像具有唯一性。
为进一步去除光照变化影响,对特征点描述符进行归一化处理。描述符向量为ξ=(ξ1,ξ2,…,ξ128),归一化后的特征向量为L=(l1,l2,…,l128),则
(7)
(3)特征点匹配。由于提取的大量特征点灰度分布比较相似,用尺度不变特征转换(scale-invariant feature transform,SIFT)算法中的欧氏距离匹配容易出现误匹配,因此采用相关系数来代替,并利用特征点主方向作为约束进行初步粗匹配。
首先判断两幅图像的特征点主方向差值绝对值是否小于给定的阈值T0,若小于T0,按照式(8)计算特征描述符的相关系数ρ,若两个特征点之间的ρ大于阈值T1,则认为是两幅图像的同名点。令T0=0.1,T1=0.7。
(8)
式(8)中:li和l′j分别为参考图像和变形图像的特征向量,n=128。
(4)确定亚像素特征点。在上一步骤中匹配得到的整像素同名点是以离散点做检测,这一步骤中将尺度看作是连续的,对函数D(x,y,σ)在x0处泰勒展开来拟合为二次函数,得
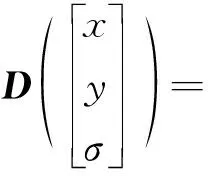
(9)
将式(9)写成矢量形式为
(10)
式(10)中:X为拟合之后连续空间下的插值点坐标,设X′=X-X0;X′为X相对于插值中心X0的偏移量。式(10)可用偏移量表示为
(11)
对式(11)求一阶偏导,令导数为零即可得到极值点相对于插值中心的偏移量为
(12)
(5)消除噪声和强边缘影响。当检测到的极值点在边缘和受到噪声干扰时,特征点会很不稳定,利用边缘上的点在横跨边缘方向上主曲率较大、在垂直边缘方向上主曲率较小的特点,可消除这一影响。
主曲率可由Hessian矩阵得到
(13)
式(13)中:Dxx(x,y)、Dyy(x,y)和Dxy(x,y)分别为DoG图像在x轴和y轴方向上的二阶导数和二阶混合偏导。由于像素点的主曲率和H(x,y)的特征值成比例,则令特征值α和β代表x轴和y轴方向上的梯度。为避免求解矩阵的特征值,计算两个特征值的比值即可。
计算H矩阵的迹和行列式值,得
Tr(H)=Dxx+Dyy=α+β
(14)
(15)
令α>β且α=γβ,其中,γ>1,于是得到
(16)
式(16)表明结果只和两个特征值的比例有关,当两个特征值相等时,式(16)最小;式(16)结果随着γ的增大而增大,即两个特征值的比值越大,表明在某一方向上的梯度越大,而另一方向上的梯度越小,这符合边缘的情况。令γ小于某个阈值,即可剔除这些边缘点。因此为了检测主曲率是否在某个阈值γ之下,只需计算式为
(17)
式(17)中:γ为经验值,取γ=10。
2.2 室内模拟实验验证
首先通过室内模拟实验对算法有效性进行验证。实验所用边坡模型由高密度泡沫制成,大小为500 mm500 mm,在模型表面涂抹不同颜色和粘贴草粉模拟岩石和植被。通过导轨移动模型,并使用百分表(MASTERPROOF 6420,精度± 0.01 mm)记录移动量。利用光源照射边坡模型,并通过改变灯的位置和亮度来模拟现实中的不同光照条件,使用数字相机(MQ013MG-E2,分辨率:1 280像素1 024像素)采集边坡模型运动过程图,实验布置如图7所示。

图7 实验布置图Fig.7 Experimental layout
实验过程中,移动平移台实现边坡模型的平移,每次移动1 mm;模型移动的同时改变光源位置并调整光源的亮度,平移台移动10次,相机记录每运动一次后的图像,拍摄得到的图像如图8所示,图中箭头为平移方向。

图8 不同光照条件下采集到的图像Fig.8 Images acquired under different lighting conditions
统计拍摄得到的边坡图像的平均灰度变化,表示实验过程中光源的亮度变化,如图9所示。结果表明,在实验过程中,光源的亮度随模型的移动,由低逐渐升高至最大亮度,然后亮度降低再逐渐升高,符合预设光强变化规律(太阳在天空中的运动)。

图9 不同光照下图像灰度变化曲线Fig.9 Gray change curve under different lighting conditions
根据本文算法对边坡模型的位移进行计算。以边坡上棋盘格的角点的位移作为标准值,根据每次移动匹配到的特征点坐标,计算各个特征点位移的相对误差。统计每次移动中,不同相对误差范围内特征点的个数,并与传统SIFT算法作比较,结果如图10所示。
从图10可以看出,基于SIFT的特征点检测能够匹配到15~20个点,相对误差小于15%;本文算法能够匹配到的特征点数为90~100,每次移动检测得到的特征点的相对误差能够控制在小于10%,由此可以证明,利用本文算法是有效的。
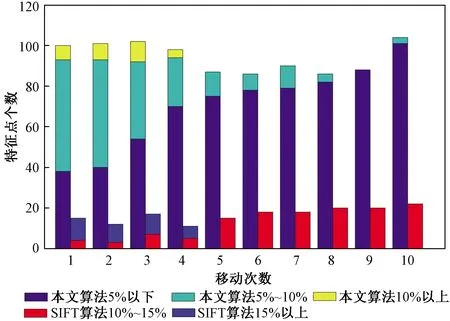
图10 每次移动的统计相对误差Fig.10 Statistical relative errors for each movement
对所有相对误差取平均,得到每次移动的平均相对误差,如图11所示。从图11可以看出,本文算法的计算精度优于SIFT算法,尤其是在初始位移量较小时,本文算法的精度远高于SIFT算法。SIFT算法的平均相对误差大于14%,本文算法的平均相对误差可以控制在小于6%。

图11 每次移动平均相对误差对比Fig.11 Comparison of mean relative errors for each movement
3 应用实例
3.1 系统搭建
为了验证本文算法在真实野外工况下的有效性,在河北省秦皇岛市青龙满族自治县承秦高速路一侧的边坡搭建了一个边坡变形监测系统,现场如图12所示。

图12 观测边坡图Fig.12 The slope image being observed
在边坡的对面一侧搭建观测系统,安装示意图如图13(a)所示,每隔14 m浇筑水泥底座,并打入螺栓与不锈钢立柱紧密固定,保证稳定性,立柱高2.2 m。选用四台海康威视的监控相机(型号:DS-2CD3T56WD-I3,分辨率:2 560像素×1 920像素)作为野外观测设备,利用抱箍将相机固定,保证了相机对各类恶劣条件的适应性。从山坡下的供电箱拉线至距离最近的立柱,利用网线为四台设备供电和图像数据传输,并将网线与光纤连接,接入高速公路的网络系统,从而实现图像的远程采集,现场安装如图13(b)所示。

图13 观测系统安装图Fig.13 Observing system installation image
3.2 测量结果
利用同一天不同时间采集到的图像(图14)验证本文算法。由于选取的是同一天的图像,且天气晴朗,无人为扰动,因此可以认为边坡未发生变形,即两幅图像的相对位移为0。根据本文算法共匹配到1 839个特征点,如图15所示,计算得到的x、y两个方向的平均绝对误差分别为0.337像素和0.271像素。

图14 不同时间下的光照图Fig.14 The slope images at different time

图15 特征点检测Fig.15 Feature points detection
从本文算法匹配到的特征点中随机选取50个点,基于灰度匹配算法计算这些点的位移量,以0像素为理论位移求取绝对误差,并与本文算法结果进行比较,如图16所示。本文算法的两个方向绝对误差的波动在0.5像素,而利用灰度匹配算法计算得到的结果与理论值相差较大,无法用于边坡变形的计算。
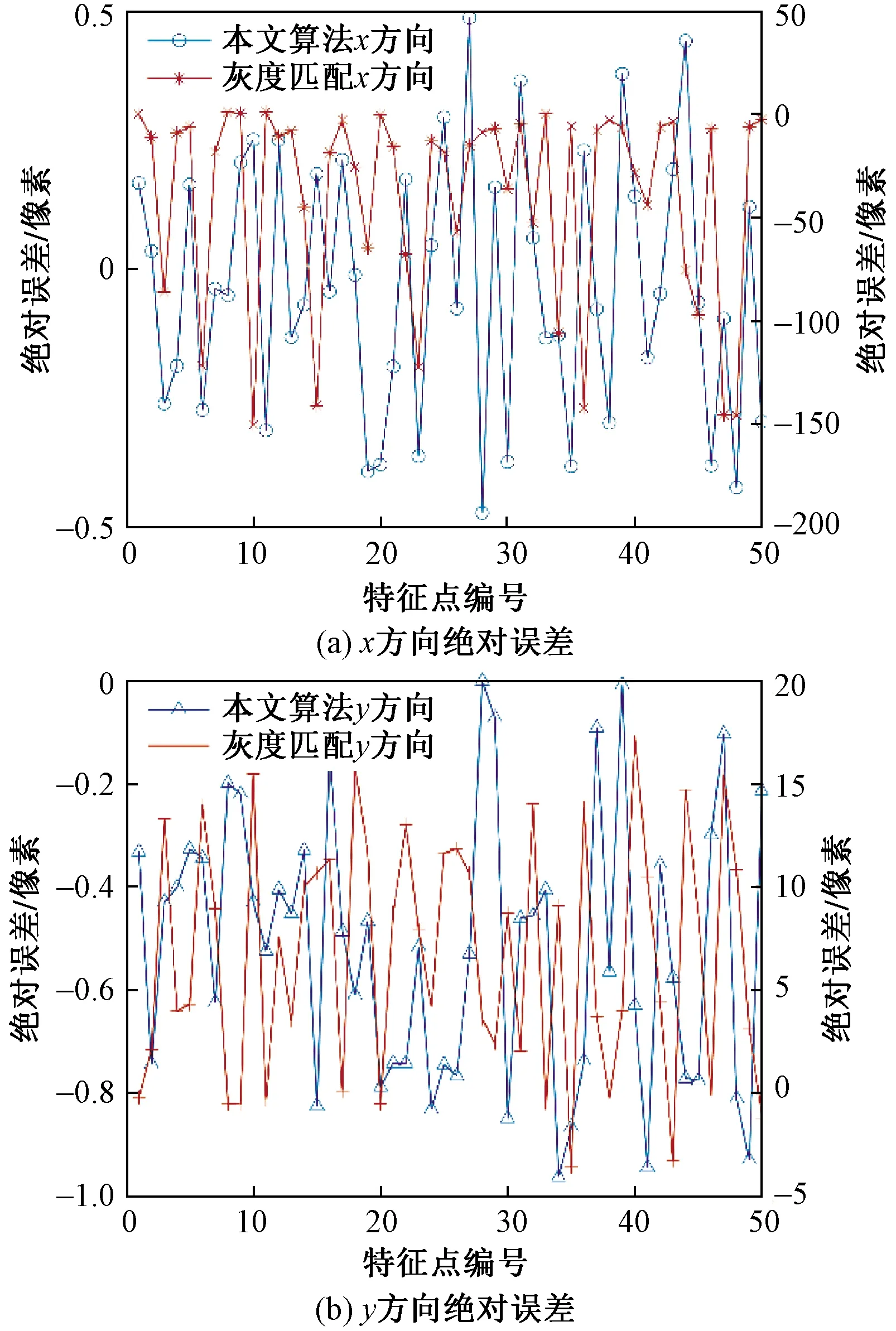
图16 x、y两个方向的绝对误差对比Fig.16 The comparison of absolute errors in x and y directions
因此,本文算法检测到的特征点数目足够可以描述整个边坡表面的位移情况,两个方向的均值误差均在0.3像素左右。根据相机分辨率和边坡实际尺寸,可得到物面分辨率为1 mm/像素,故测量分辨率为0.3 mm,完全符合精度要求。
4 结论
为了解决野外边坡摄像测量中光照变化对测量精度影响的问题,发展了一种抗光照的特征点提取与匹配算法,获得了很好的效果。主要结论如下。
(1)将特征点周围的局部灰度梯度的主方向作为特征量,结合匹配算法,实现了抗光照变化能力与匹配稳定性的变形分析。
(2)通过野外边坡实验验证了本文算法的可行性,与传统算法相比匹配点数更多、测量精度更高。
本文算法为边坡变形摄像监测提供了一种新的手段,同时也可以有力支撑该方法在航空航天和土木交通等领域的应用。在后续研究中,可将此方法扩展至三维变形测量,研究不同位置和视角图像(含不同光照变化特征)间的特征点匹配,进一步扩展本文算法的应用范围。
