柔性中压直流配电网的新型电流差动保护方案

2021-04-13刘静，吕睿

科学技术与工程 2021年7期

刘静，吕睿

(中国矿业大学(北京)机电与信息工程学院，北京 100083)

近年来，化石能源短缺以及环境污染问题日益突出，世界各国越来越重视可再生能源的开发利用，比如光伏、风电。伴随着配电网中分布式可再生能源的大量接入，再加上风电、光伏等可再生能源发电的波动性，导致潮流均衡协调控制愈发复杂，如何保证含分布式能源配电网的安全可靠已然成了一大难题[1]。而基于模块化多电平换流器(modular multilevel converter, MMC)的柔性中压直流配电网被认为是一种解决分布式能源接入问题的有效技术方案[2-3]。

对于多电平换流器并网的直流配电网，故障电流上升快且不存过零点，换流站中的绝缘栅双极型晶体管(insulated gate bipolar translator，IGBT)等电力电子期间受到电流冲击时极易发生损坏，这对直流配电网的继电保护系统提出了极高的要求[4-5]。现有的直流系统主要利用行波保护作为主保护，但是其在发生高阻故障、电压变化很小时的可靠性不高，需要利用电流差动保护作为后备保护[6]。目前应用的电流差动保护，由于受到故障初期分布电容电流的干扰，保护会先延时一段时间，此后的保护装置动作本身就需要500 ms左右的延时，这意味着即使保护能够正确动作，从发生故障到保护装置动作也需要大约1 s的延时[7-8]。这段延时可能会导致故障电流上升到较大值，而触发换流站处的保护，导致在电流差动保护动作前换流站就已经闭锁，扩大故障停电范围。

为了避免这个问题，中外学者已经进行了相关研究。这些研究的主要目标都是减少保护所需的延时，按照方式不同可以分为两类：减少通信所需的延时和减少躲过分布电容电流所需的延时。文献[9-10]利用磁环作为线路边界设计了基于单端电气量来设计保护判据，直接消除了收集线路两端信息所需的时间，但这类方法的可靠性还有待实践检验。而对于直流配电线路，线路长度相对较短，通信所需的延时较少，因此可以直接通过改良传统电流差动保护来提高可靠性。文献[11-12]以架空线路为研究对象，基于贝瑞隆线路模型，通过极模转换采用不同的方法计算差动电流。这种方法忽略了线路的频变特性，导致在极对地故障时会出现健康极的误跳。对于架空线路来说，频变特性的影响较小，这种方法有一定的可行性，然而对于柔性中压直流配电网来说，多用电缆作为传输线，电力电缆的结构特点和敷设环境决定了它的电容效应和频变效应，相较于架空线路会更加明显。对于电容效应，由于电力电缆的几何参数很小且绝缘层的介电常数很大，因此其电容效应比架空线路明显得多[13]，使得电力电缆中的分布电容电流更大。而对于频变效应来说，一方面，电力电缆内部分层的多导体结构加深了集肤效应[14]对截面电流分布的影响；另一方面，电力电缆大多与土壤直接接触使得大地返回效应更加明显。这样，在短路故障暂态，不同频率的电流波在线路上传播时就会具有不同的传播速度和衰减速度，使得频变效应更加明显。因此，之前忽略线路频变效应的方法就不再适用，亟需研究能够适用于电缆线路的电流差动保护方法。

目前，部分学者提出了一些适用于电缆线路的电流差动保护方法。文献[15]基于频变线路模型，对所得到的测量信号在2 ms的时间窗内进行时频域转换来计算差动电流，有效消除了分布电容电流的影响，但计算时间较长；文献[16]中提出了一种基于补偿点电流作为判据来补偿分布式电容电流影响的电流差动保护方案，同时在频域上推导了考虑频率特性传输线上的电压与电流计算公式;文献[17]基于输电线路等传递过程理论(equal transfer process of transmission lines, ETPTL)，同一低通滤波器对线路两端的电压、电流信号进行足够低的截止频率处理后，可以将线路上的电压分布视为线性分布，通过对线性分布电压的积分，计算并补偿分布电容电流，改进传统的电流差动保护。但是，这些方法均需要较大的计算量，对运算速度提出了较高的要求。

基于上述问题，如何减小乃至消除电力电缆线路频变效应和分布电容电流对电流差动保护的影响，并且保护动作快速可靠，成了柔性直流配电网电流差动保护的关键研究点。现针对含电缆线路的柔性中压直流配电网，提出一种基于贝瑞隆模型的新型电流差动保护方案，可消除分布电容电流的影响，其计算方法简单且可靠性高，最后验证了该方案提高电流差动保护速动性的有效性。

1 基于贝瑞隆模型的新型电流差动保护方案

1.1 贝瑞隆模型

贝瑞隆模型利用行波理论，用行波的观点分析电磁波在线路的传播过程来解释暂态过程[18]，将线路近似成无损传输线，是最简单的分布参数模型，它反映了内部无故障的线路两端电压与电流之间的关系，如图1所示。

图1 单根无损线路贝瑞隆等效模型Fig.1 Bergeron equivalent model for single lossless circuit

贝瑞隆域形式为

(1)

式(1)中：uj(t)、ij(t)和uk(t)、ik(t)分别为j端和k端的电压、电流在t时刻的测量值；Zc为线路波阻抗；Ijk(t-τ)和Ikj(t-τ)分别为线路两端的等效电流源，计算公式为

(2)

式(2)中：τ为电磁波通过线路全长所需的时间。

在实际情况中由于需要考虑损耗，可以采用分段的思想将线路作为集中电阻串入无损线路中，可以得到考虑损耗线路贝瑞隆模型的时域形式为

(3)

式(3)中：Z=Zc+R/4为考虑损耗后的等效波阻抗。

令h=(Zc-R/4)/(Zc+R/4)，R为线路全长等效电阻。

(4)

1.2 基于贝瑞隆模型的新型电流差动保护原理

由前文可知，造成常规电流差动保护性能较差的原因是分布电容电流的影响和电力电缆频变特性的影响。而贝瑞隆模型是一种线路分布参数模型，是消除分布电容电流影响并提高电流差动保护性能的一种有效方法。根据前文推导的单根无损线路的贝瑞隆模型，式(1)可变形为

(5)

线路内部发生故障时单根无损线路如图2所示。

图2 发生内部故障时的单根无损线路Fig.2 Single lossless circuit in case of internal failure

将式(5)分别应用于j与故障点f、f与k之间的线路，通过t和t-τj相互代替消去uf(t)可得

(6)

式(6)中：τj为电磁波从j端传播到f点所需的时间。由无损线路的贝瑞隆模型可知，j端通过贝瑞隆模型计算得到的计算电流icj(t)为

(7)

因此，式(6)可以写为

ij(t)-icj(t)=if(t-τj)

(8)

由式(8)可知，有内部故障发生于无损线路中时，线路j端实际电流与线路j端通过贝瑞隆模型计算得到的电流之差为故障电流。由于实际线路存在损耗，应采用考虑线路损耗的贝瑞隆模型获得参考点的计算电流，即

(9)

式(9)中：R0为单位长度线路电阻；x为线路j到故障点f的距离；v为波速。

因此，可以在线路上任选一个参考点m。分别通过测量保护安装处j端k端和的电压、电流uj、ij和uk、ik，利用式(9)计算参考点m左侧和右侧的电流icjm和ickm，二者并非此处的实际电流，而仅为计算电流。当没有区内故障发生时，线路相当于一段贝瑞隆模型等效线路，此时从j端计算的m点左侧故障电流icjm和从k端计算的m点右侧故障电流ickm相等；而线路发生区内故障时，线路不再是一段贝瑞隆模型等效线路，而是j-m和m-k两段，此时从j端计算的m点左侧故障电流icjm和从k端计算的m点右侧故障电流ickm的差值波形可以很好地反映故障电流的波形。由以上讨论的电流差动保护方法，可以构造判据，即

(10)

式(10)中：idiff是利用线路两端保护安装处的电压电流采样值通过贝瑞隆模型计算得到的参考点m两侧的差电流；iset是电流差动保护的电流阈值，可以采取如下方法来确定：首先确定最大不平衡电流，主要包括各种区外故障时可能出现的不平衡电流和区内不对称故障时非故障极的不平衡电流。然后，将最大不平衡电流与可靠系数相乘，即可得到电流阈值。这样，基于贝瑞隆模型的电流差动保护在原理上已经考虑了分布电容电流的影响，因此在应用中不再需要通过延时来躲过分布电容电流的影响，可以有效地改进常规电流差动保护动作时间较长的问题。

2 算例仿真及分析

为验证所提的基于贝瑞隆模型的新型电流差动保护的有效性和优越性，在PSCAD/ ETMDC上搭建了伪双极±20 kV的中压双端直流配电系统，其中传输线为直流电缆，线路n-j和线路j-k的长度均为10 km，换流站均为模块化多电平换流站，取线路j-k中点为参考点m，如图3所示，其中Bus为母线。

图3 ±20 kV中压三端直流配电系统Fig.3 ±20 kV medium voltage three-terminal DC distribution system

2.1 常规电流差动保护

要保证直流系统的差动保护能够正确可靠动作，必须保证其能够正确区分最严重的区外故障和故障电流最小的区内故障之间的差别。对于直流双极系统，故障电流最小的区内故障为区内高阻接地故障，故障电流最大的区外故障为区外近端金属性接地故障。而对于直流伪双极系统，发生接地故障时的故障电流很小，考虑区内双极高阻短路故障和区外近端双极金属性短路故障。

系统启动后0.6 s时分别在k端右侧和距离j端3 km处分别引入双极金属性短路故障和双极高阻短路故障，对于j-k线路的电流差动保护分别对应区外故障和区内故障，研究其差动电流的故障暂态特性，如图4所示。

图4 区内故障和区外故障的暂态差动电流Fig.4 Transient differential current for in-zone and out-of-zone faults

由图4可以看出，区内高阻故障时，在故障暂态阶段计算得到的差动电流与实际故障电流的暂态波形有较大的出入，且最大值在0.25 kA左右。而区外近端金属性故障时的差动电流有最大值，且在0.4 kA左右的波动。很显然，此时常规电流差动保护无法正确区分区内双极高阻短路故障和区外近端双极金属性短路故障，需要设置延时来躲过电流交叉部分。这种电流的波动实际上是由线路分布电容电流和直流电缆线路的频变特性共同作用产生的。

2.2 基于贝瑞隆模型的新型电流差动保护

为验证以上所述的基于贝瑞隆模型的新型电流差动保护方案对于提高电流差动保护速动性的有效性，根据前文介绍的电流差动保护方案，分别在区内双极高阻短路故障和区外近端双极金属性短路故障时的差动电流特性，并与常规的电流差动保护方案进行对比。两种保护方案的故障暂态差动电流曲线如图5所示。

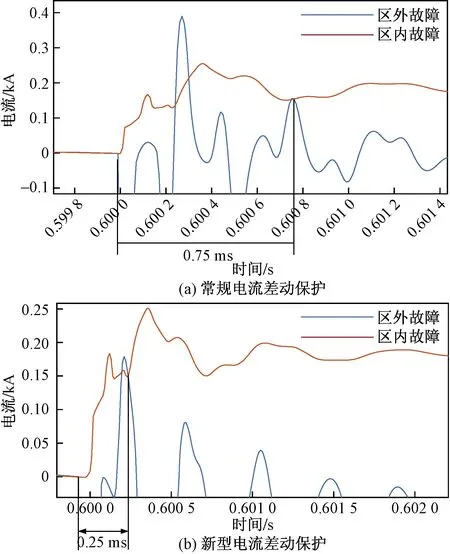
图5 两种电流差动保护故障暂态差动电流对比Fig.5 Comparison of transient differential current between two current differential protection faults

由图5(a)可知，区外近端双极金属性短路故障时的差动电流与区内双极高阻短路故障时的差动电流存在两次交叉，这样就需要延时来躲过这两次交叉，再判断是否发生故障，这段延时约为0.75 ms。而对于图5(b)所示的新型电流差动保护，区外近端双极金属性短路故障时的差动电流与区内双极高阻短路故障时的差动电流只存在一次交叉，因此只需要延时0.25 ms。这样，使用这种新型电流差动保护可以缩短近2/3的延时，有效提高了电流差动保护的速动性。