基于三次样条插值的频域频偏估计算法研究

张少侃，梁中英，高心炜

（广州海格通信集团股份有限公司，广东 广州 510663）

0 引 言

在目前的数字通信系统中，收发端载波频偏的存在会使通信系统的性能急剧恶化。文献[1-3]都对频偏估计问题进行了深入的研究与讨论，可见研究频偏估计问题具有重要的意义。

目前，常见的数字通信系统中，数据辅助的频偏估计算法由于其精度高、估计范围广，因而受到了更多的关注。数据辅助的频偏估计算法主要分为两大类，分别是基于时域分析的估计方法和基于频域分析的估计方法。实际系统中常用的时域估计方法有Kay算法、Fitz算法、M&M算法以及L&R算法[4-7]。在时域算法中，综合考虑估计范围和估计精度，M&M算法是不错的选择，但其对信噪比比较敏感，即使在低信噪比下，估计性能也会恶化。在频域算法中，基于快速傅里叶变换（Fast Fourier Transformation，FFT）变换对频谱进行精确插值的频偏估计算法比较常见[8]。此种算法频偏估计范围广，对信噪比不敏感，常常受到众多通信系统的青睐。但是由文献[9]可知，由于FFT自身的栅栏效应，估计精度和有用数据个数以及FFT变换点数有关，因而对于估计精度要求比较高的系统常常难以满足要求。二次抛物线频域内插频偏估计方法虽然使得估计精度有所提高，但此种方法因为只用到二次拟合,且没有分区间段拟合，所以估计精度提高程度有限，仍然很难满足很多系统的精度要求。

本文根据拟合理论，对FFT变换后的频谱进行分段拟合。每段使用三次函数进行拟合，从而提高了拟合精度。另外，本文从基本代数理论出发，推导出了分段三次函数拟合的插值公式。仿真结果说明了三次样条插值算法的估计误差在低信噪比下仍能接近修正的克拉 - 美罗界（Modified Cramer-Rao Bound，MCRB），与二次插值算法相比，其估计误差更接近修正的克拉-美罗界，且复杂度没有提高，因而将会有更好的应用场景。

1 频域频偏估计方法

本文考虑物理传输信道模型为加性高斯白噪声（Additive White Gaussian Noise，AWGN）信道，且接收端信号已经实现了位同步，则接收端收到的基带离散信号可以表示为：

式中，T为符号周期时间；N为符号个数；sk为基带信号的复数形式；Δf为接收基带信号的频率偏差；nk为加性复高斯白噪声，其均值为0，方差为σ2。

FFT 是离散傅里叶变换（Discrete Fourier Transform，DFT）的一种快速算法，是工程实践中可实现的方法。FFT频域频偏估计算法的基本思想是搜索接收端去调制信号频谱图的峰值。理论上去调制信号频谱图的峰值位置为零频位置，当信号带有频偏时，峰值位置便为频偏值的位置，因而峰值位置即对应于载波频偏。FFT作为频域频偏估计算法，其不但频偏估计范围大，可以达到50%的符号速率，而且还能够在很低的信噪比下工作。此外，由于使用快速傅里叶变换实现的复杂度低，因此在实际系统中得到了广泛应用。DFT频域估计算法和频率估计分别可以表示为：

式中，Nfft为DFT变换点数；sk*是信号sk的复共轭形式；为所要估计的频偏值。

2 三次样条插值算法

三次样条插值算法的基本思想是在利用基带去调制信号频谱图峰值进行频偏粗估计的基础上，根据三次样条插值公式，利用峰值及其左右两条谱线的幅度进行细估。根据FFT得到频谱能量的最大值A(km)及其对应的频率点km，同时可以得到最大值A(km)左右相邻的两个值A(km-1)和A(km+1)，及其对应的频率点km-1和km+1。根据这3点可以对构成的两个区间段进行独立的三次样条插值曲线拟合，最后在两个区间段中找到估计的最大值位置k以及下面给出三次样条插值的定义及求解过程。

2.1 三次样条插值定义

令x0=km-1，x1=km，x2=km+1，对应的y0=A(km-1)，y1=A(km)，y2=A(km+1)。样条曲线S(x)是一个分段定义的光滑曲线，其分段函数曲线用三次多项式进行拟合，两个分段函数可写为：

式中，a0，a1，b0，b1，c0，c1，d0，d1代表8个未知系数。

2.2 三次样条插值求解

根据前面的定义，步长h=x2-x1=x1-x0=1，将其带入以下条件中。

（a）由Si(xi)=yi,i=0,1 可以推导出：

（b）由Si(xi+1)=yi+1,i=0,1可以推导出：

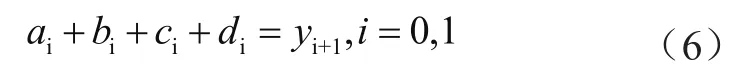
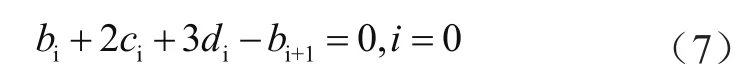
从式（5）到式（8）可知8个未知数有6个方程，还需要两个方程才能求解出8个未知数。根据FFT变换的平滑性可知，曲线两端没有受到任何让它们弯曲的力，即这样便可以得到：

联立式（5）到式（9）就可以求解出8个未知数，求解的结果为：

得到了8个未知系数后，便得到了两段区间的光滑曲线函数表达式，根据三次函数的特性，可以求解出两个区间段内的最大值点为：

对式（11）求解二次方程的根可得：

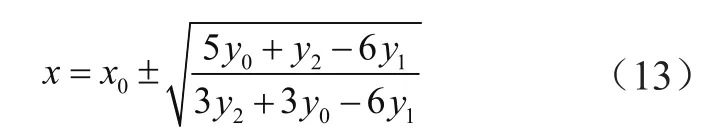
根据前面y0、y1、y2的定义可知，y1＞y0，y1＞y2，因此根号里面的分数值大于零。又因为三次曲线是建立在各段区间内的函数，而区间段长度h=1，所以对于式（13）取区间段内的根值为：

同时要求：

也即当y2＜y0时，在区间段[x0,x1)内，存在三次光滑曲线函数S0(x)的最大值，否则最大值不存在于区间段 [x0,x1)内。

对式（12）求解二次方程的根可得：

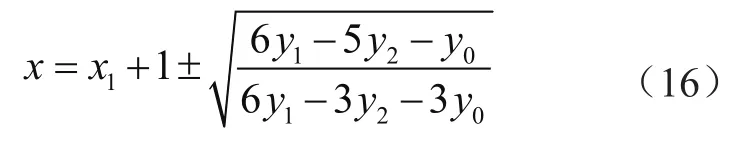
根据y1＞y0，y1＞y2可知，根号里面的分数值同样大于零。同理，因为三次曲线是建立在各段区间内的函数，区间段长度h=1，所以对于式（16）取区间段内的根值为：

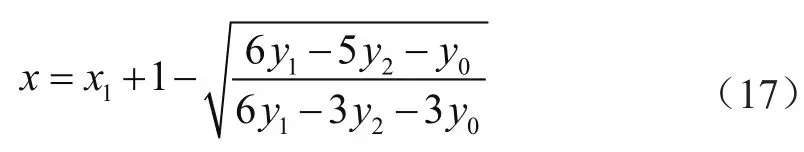
同时也还要求：

也即当y0＜y2时，在区间段[x1,x2)内，存在三次光滑曲线函数S1(x)的最大值，否则最大值不存在于区间段 [x1,x2)内。

2.3 三次样条插值算法总结

综上所述，下面给出三次样条插值算法的频域频偏估计算法具体步骤。

步骤1：对接收到的基带去调制信号进行快速傅里叶变换，找到频域峰值坐标点(km,A(km))及其左右两点 (km-1,A(km-1))与 (km+1,A(km+1))。

步骤2：判断A(km-1)与A(km+1)的大小，如果A(km-1)＜A(km+1)，则转入步骤3；如果A(km-1)＜A(km+1)，则转入步骤4。

步骤3：此时计算估计出的最大值位置为：

转入步骤5。

步骤4：此时计算估计出的最大值位置为：

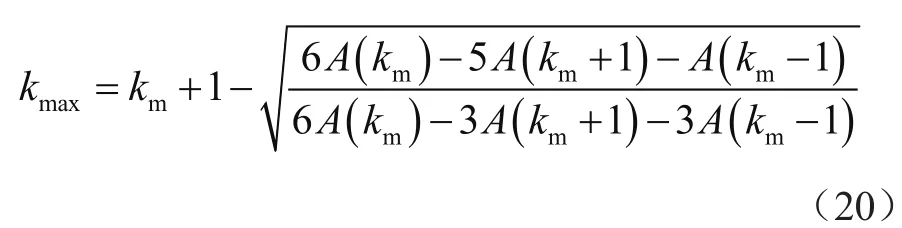
转入步骤5。

步骤5：计算频偏估计值为：

3 仿真分析

对本文提出的基于三次样条插值频域频偏估计算法进行MATLAB仿真分析。选取直接FFT频域频偏估计算法和二次插值频域频偏估计算法与本文提出的三次样条插值算法做比较，对于FFT频域频偏估计算法：

对于二次插值频域频偏估计算法：

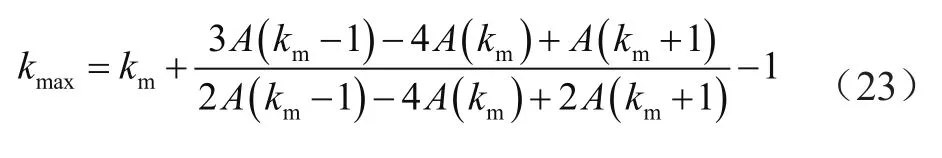
首先会对3种算法的频偏估计范围做仿真分析，研究它们在不同大小频偏下的频偏误差均值，然后将频偏估计结果与CRB进行比较。文献[10]给出了信号载频频偏估计的MCRB，具体为：

式中，ES表示每个符号的能量；σ2表示复噪声的功率。本文使用MCRB指标来对比算法的性能。

仿真设置调制方式为正交相移键控（Quadrature Phase Shift Keying，QPSK），假设接收有用的去调制符号个数N为64，信道为加性高斯白噪声信道，初始相移由随机函数产生，FFT的点数设置为256，蒙特卡洛实验统计次数设置为1 000次。

3.1 频偏估计范围仿真分析

设置系统符号速率为4 ks/s，频偏值的变化范围为-2～+2 kHz，间隔为10 Hz，信噪比（Signal-to-Noise Ratio，SNR）=-10 dB，使用FFT算法、二次插值算法以及本文提出的三次样条插值算法估计出的频偏估计归一化均方根误差随系统归一化频偏的变化曲线如图1所示，归一化步进为0.025。

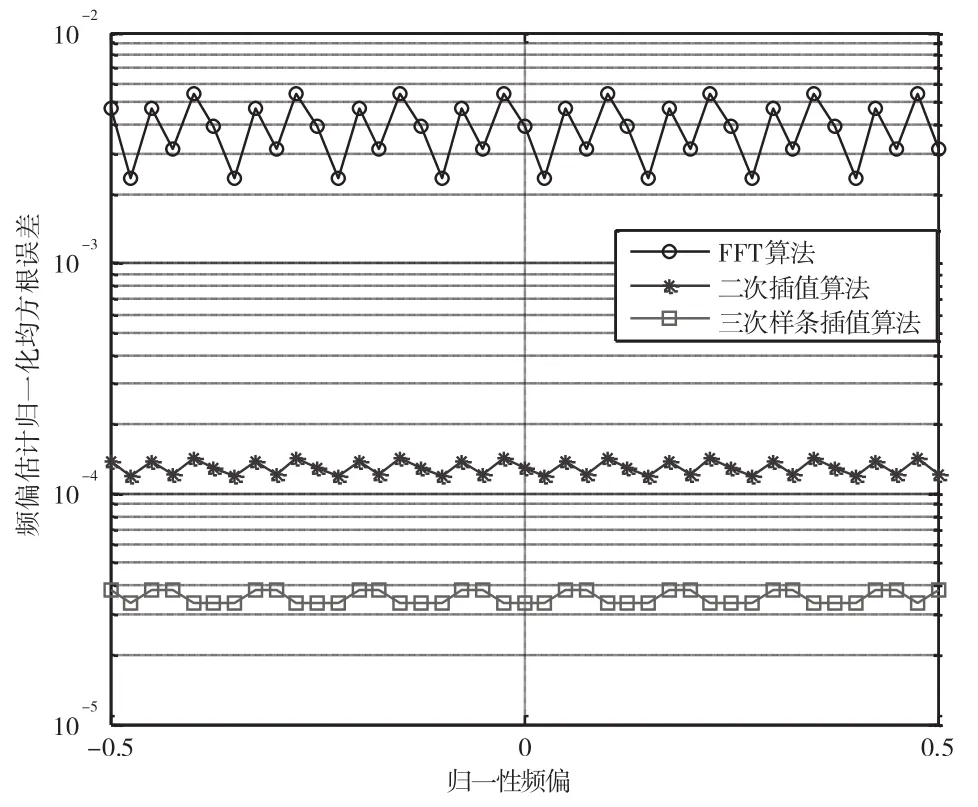
图1 不同算法的归一化均方根误差随频偏变化曲线

从上述仿真结果可以看出，3种算法均能在[-sr/2,sr/2]的频偏范围内工作，而且本文提出的三次样条插值算法的归一化均方根估计误差在任何频偏下都比FFT算法和二次插值算法的归一化均方根估计误差要小，有力地说明了本文给出的三次样条插值算法在[-sr/2,sr/2]的频偏范围内均可以正常工作。

3.2 频偏估计算法性能的仿真分析

设置系统符号速率为4 ks/s，频偏值大小在[-sr/2,sr/2]的范围内随机产生，系统信噪比值的变化范围为-10～+10 dB。FFT算法、二次插值算法以及本文给出的三次样条插值频偏估计算法的频偏估计归一化均方误差和MCRB随信噪比值变化的曲线如图2所示。

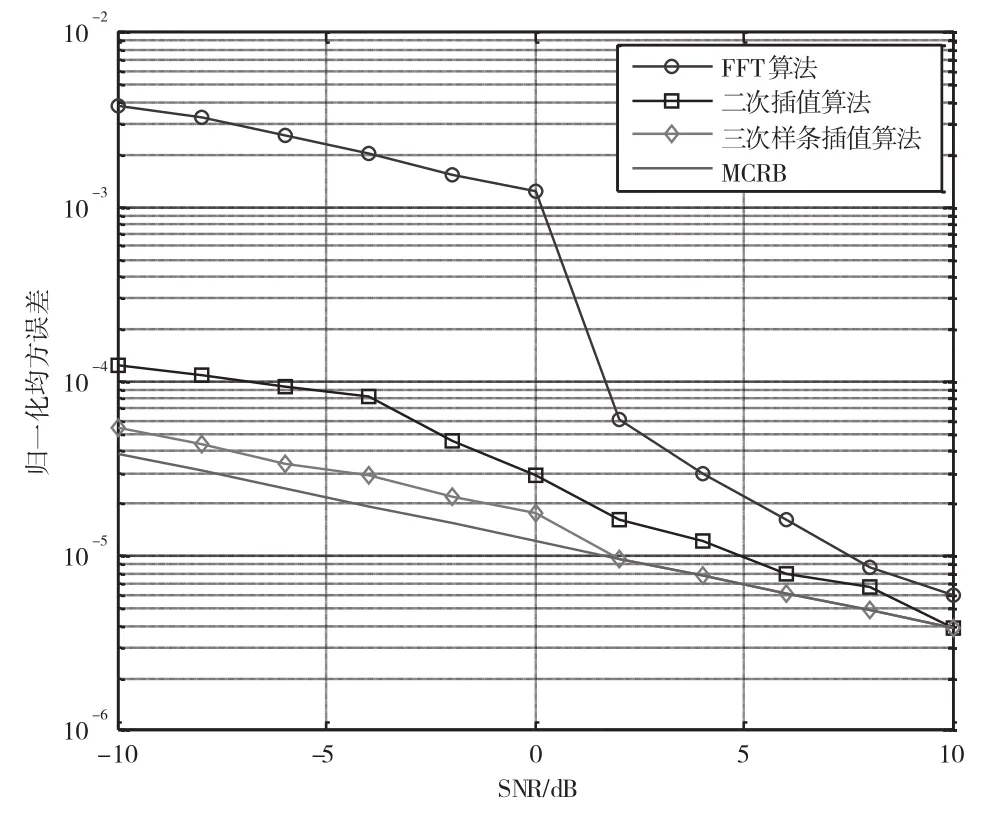
图2 不同算法的频偏估计归一化均方误差与MCRB的比较曲线

从上述仿真结果可以看出，随着信噪比的增加，各种算法的误差曲线都在向MCRB曲线靠拢，但是在低信噪比下，三次样条插值算法的误差明显更接近于MCRB曲线，且不会随着信噪比的降低急剧增大。

4 结 论

针对FFT栅栏效应对频域频偏估计算法造成的精度问题，本文根据拟合理论以及基本代数理论建立了FFT变换后频谱分段拟合模型，并通过详细推导，求解出了三次样条插值函数的最大点内插公式。最后，通过MATLAB仿真对比了FFT频域频偏估计算法、二次插值频域频偏估计算法以及三次样条插值频域频偏估计算法的估计范围和均方误差，有效地说明了本文提出的三次样条插值频域频偏估计算法的可行性与有效性。