基于FELMS算法改善车内声品质

赵向阳,周慧琳,吴启斌

(1.河南工学院 车辆与交通工程学院， 河南 新乡 453003；2.河南工学院 材料科学与工程学院， 河南 新乡 453003)

0 引言

声品质反应了人对噪声的主观心理感受，是当前噪声评价研究的热点之一。研究表明，声品质主要受某些客观参量影响，如响度、尖锐度及粗糙度等，其值与声波的振幅、频谱相关[1]。由波的独立传播性和矢量叠加性，当两列具有固定相位差的波在空间相遇时会产生干涉现象，基于此发展起来的噪声主动控制(active noise control, ANC)技术可人为发出次级声波与目标区域初始噪声进行叠加抵消，进而达到降噪的目的，具有主动性、选择性等优点，在声品质的改善中有独特优势。

当前声品质的噪声主动控制依据系统结构主要分为主动噪声均衡(active noise equalizer, ANE)系统和滤波误差最小均方(filter-error least mean square, FELMS)系统两类。吉林大学王登峰团队对ANE系统进行了实车噪声主动控制研究，结果表明，响度下降了25 %左右，尖锐度下降了10 %左右[2]；苏丽俐将车内噪声按照豪华感、运动感等进行了多维度的评价，利用ANE系统在不同维度下进行了噪声主动控制，取得了较好的优化效果[3]。但ANE系统中的增益系数求解复杂，处理芯片性能对系统实时性影响较大，实际应用中成本较高，而FELMS算法设计的ANC系统，结构简单且计算量相对较小。SOMMERFELDT验证了该算法对响度控制的可行性[4]；东南大学姜顺明针对响度优化了FELMS系统中的残差滤波器设计，仿真控制后响度取得了31.3 %的降幅，控制效果明显[5]。但在此类研究中，大多数学者只考虑了响度，控制变量单一且未考虑控制频段范围对声品质控制效果的影响。

针对研究现状中存在的不足，本文基于高预测精度的最小二乘支持向量机(least squares support veotor machine, LS-SVM)声品质预测模型，首先选取对声品质影响最大的响度作为被控的心理声学客观参量，根据特征响度的大小确定响度的控制方法，然后对样本信号进行互补集合经验模态分析(complementary ensemble empirical mode decomposition, CEEMD)分解重构，依据每个本征模态函数(intrinsic mode function, IMF)分量对声品质的影响程度确定声品质的控制方法，最后在考虑控制频段大小对系统性能影响的情况下进行仿真研究，经对比和二次主观评价验证，基于CEEMD分解重构的声品质主动控制效果优于只针对响度进行主动控制，研究思路和方法对声品质的主动控制具有较高的参考价值。

1 LS-SVM声品质预测模型

可靠且精确的声品质预测模型是进行声品质主动控制研究的基础，本节将首先进行稳态噪声样本信号的采集试验，然后对信号进行筛选和处理等，得到最终的有效样本，最后针对支持向量机的缺陷，利用最小二乘法对其进行优化，建立LS-SVM预测模型，实现声品质客观评价。

1.1 噪声信号的采集及处理

Head Acoustics公司在声品质研究方向有一套完整的软硬件解决方案，本次噪声信号采集选用该公司的SQuadriga四通道便携式采集前端以及内置声音传感器的BHS耳机，因SQuadriga有内置电源，在实车试验时无需连接供电设备，且BHS耳机可直接由驾驶员佩戴，所录取的信号能准确地反应驾驶位耳旁处的真实噪声，信号的后处理同样基于Head Acoustics公司的Artemis 12.0软件。噪声信号的采集如图1所示。

(a) SQuadriga四通道便携式采集前端

试验时车窗需保持密闭，空调关闭，外部环境要求无车辆通过、鸣笛等情况，选取的实验道路为城市郊区平坦的柏油路，综合考虑安全性和道路限速，试验车速度为怠速到90 km/h，利用定速巡航功能待车速稳定，开启SQuadriga，驾驶员佩戴的BHS耳机将会录取耳旁处噪音信号，并以hdf的数据格式存储，试验结束后可通过USB接口与计算机相连接将信号导出进行后处理。需要注意的是，信号采集时，若屏幕显示0 V则表明存在外界强干扰，信号已被污染，需删除并重新进行采集。本次试验中，以5 km/h为步长，每个车速下采集5组信号，通过FFT vs Time分析选择其中最为稳定的3组信号作为该车速下的稳态噪声样本。完成采集后筛出平稳的噪声信号导入Artemis 12.0软件中，经过截止频率为20 Hz的高通滤波及等响处理共得到54个有效的噪声样本信号，并对客观参量进行计算。

样本信号的声品质可通过主观评价来获得，本次组织的评审团成员均有2年以上的驾驶经验，并在正式评价前挑选了5种典型声音样本进行了听音训练。用烦恼度表征声品质，将其划分为5个等级，每个等级下又划分不同分值，评分表如表1所示。评审团共计22人，男女比例为7∶4，采用Sennheiser HD专业鉴定耳机在安静的会议室中回放样本信号，评审员依据等级划分评价表进行主观烦恼度打分。为保证主观评价结果具有统计学意义，需要对所有主观评价结果进行一致性以及可靠性检验，并对通过检验的评价结果求均值得到每组样本的主观烦躁度等级。54组噪声样本信号的客观参量值及其烦恼度等级如表2所示。

表1 等级评分法评分表

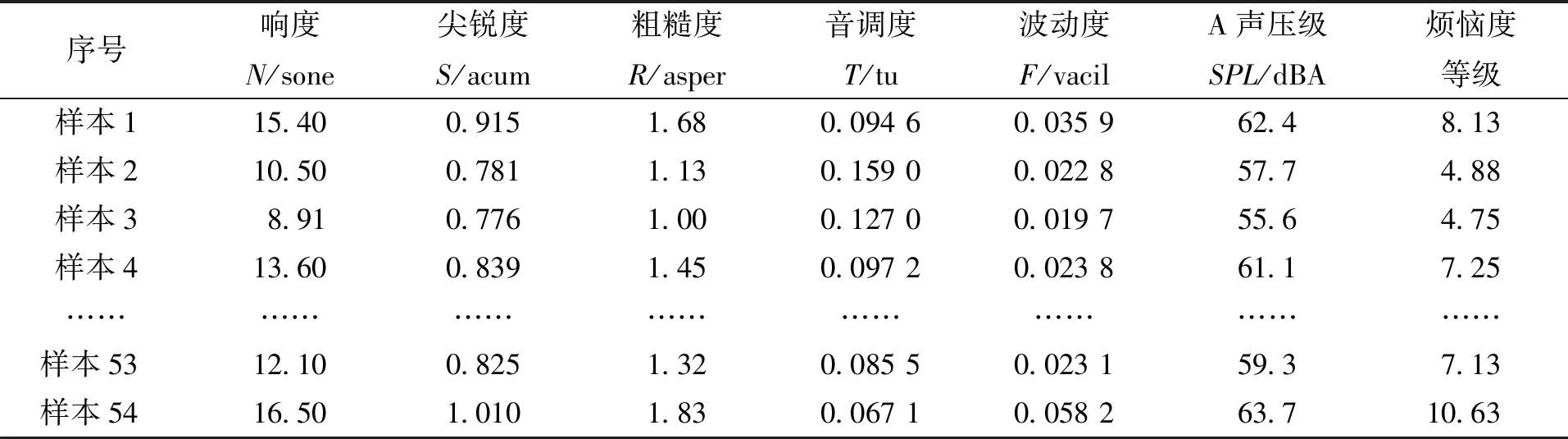
表2 客观参量计算结果及烦恼度等级

1.2 LS-SVM声品质预测模型

传统的声品质预测模型大多基于神经网络进行建模，比如较为成熟的遗传算法和反向传播算法相结合(genetic algorithm back propagation, GA-BP)神经网络模型，虽然引入了遗传算法对神经网络进行了优化，避免陷入局部最小，但该模型同样需要大量的样本进行训练才能获得较好的预测精度，对于小样本、多维问题识别精度往往不足。因受试验环境以及时间限制，本文共计只采集了54组有效信号，样本量小且选取的声品质客观参量多达6个，神经网络的建模方法并不适用，然而基于间隔最大化学习策略发展起来的支持向量机能完美地解决该问题，但因其为不等式约束，求解复杂[6]。为简化求解过程，可引入最小二乘法改变其约束关系，将支持向量机的松弛变量作为训练目标，不等式约束就变为了等式约束，形成了改进后的LS-SVM[7-8]，将问题归结为求解方程组。建立LS-SVM声品质预测模型的步骤如图2所示：

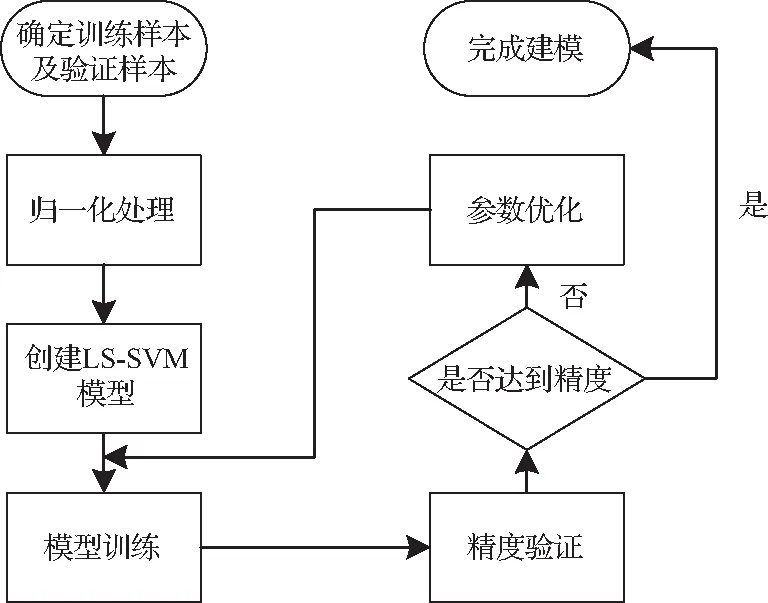
图2 LS-SVM声品质预测模型建立流程

① 将样本1～44作为训练样本，样本45～54作为验证样本；

② 对训练及验证样本进行归一化处理，避免量纲不同影响模型预测精度，归一化公式如式1，(其中，G为归一化后的值，xmin和xmax分别为该组数据种的最小值和最大值)：

(1)

③ 基于MATLAB搭建LS-SVM模型，并确定模型所使用的核函数，在此选择径向基函数为模型的核函数，使用网格交叉法寻找最优的惩罚因子gam以及径向基核函数中的核参数sig；

④ 使用1～44号样本进行模型训练，并使用样本45～54进行预测精度的验证；

⑤ 达到目标预测精度，完成建模。

按照上述步骤进行建模，为验证LS-SVM方法的正确性，同时建立GA-BP模型进行对比，样本45～54验证样本的预测结果如图3所示，LS-SVM模型拟合系数R2=0.958，平均误差仅为3.61 %，而GA-BP模型拟合系数R2=0.936，平均误差4.77 %，LS-SVM模型的拟合效果及平均误差均优于GA-BP模型，样本声品质的模型预测结果与主观评价结果得到了良好的拟合，所建立的LS-SVM声品质预测模型具有较高的预测精度，证明所选方法的正确性。

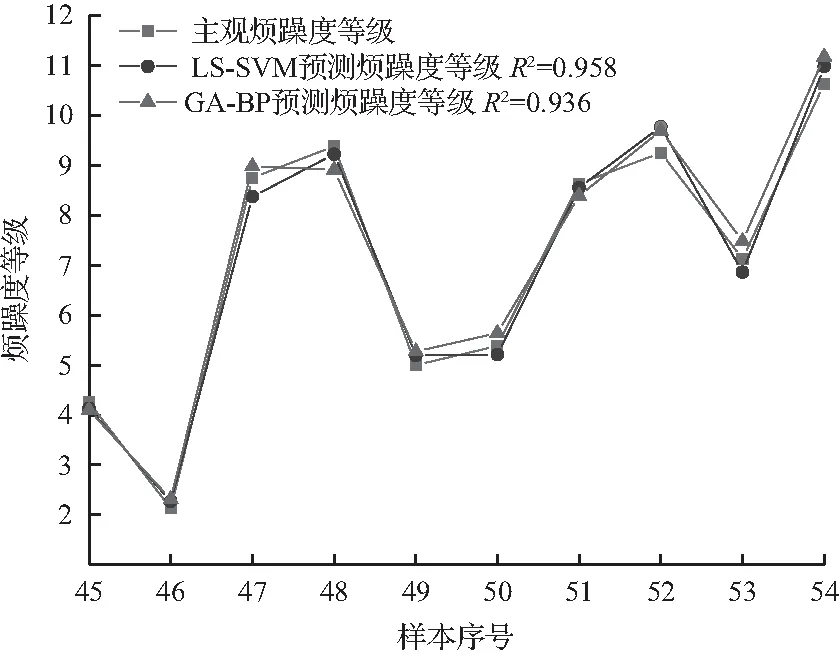
(a) 验证样本烦躁度等级

2 声品质控制策略分析

2.1 回归分析

每个客观参量对声品质的影响程度不一，为量化描述二者之间的关系，在SPSS软件中回归分析，结果见表3。回归产生的Pearson系数绝对值越大表明相关性越强[9]，由表可知，音调度与声品质为负相关，即音调度越大声品质越好，符合人对声音的主观反应，除音调度外，其余各参数与声品质均为正相关，即其值越大声品质越差，其中响度、粗糙度与烦躁度的相关系数均超过了0.8，呈显著相关性，是影响声品质的主要客观参量。

表3 Pearson相关系数

2.2 响度分析

由上文回归分析可知，响度与声品质的关联程度最大，因此首先分析对响度的控制策略。ISO532国际标准中规定了2种响度计算方法，其中Zwicker法因可适应多种声场被广泛使用[10]，计算公式见式(2)：

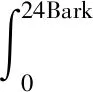
(2)

式中，N为总体响度;N′(z)代表在Bark域下的特征响度，其计算方法见式(3)：

(3)

式中，E为激励级;ETQ为听阈激励;E0为参考激励。

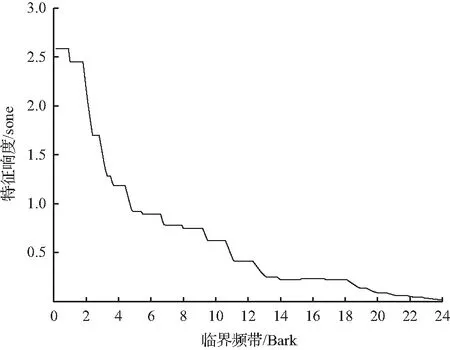
图4 52号样本特征响度曲线

图4为52号样本的特征响度曲线，结合式(2)可知，总体响度为特征响度曲线与坐标轴所围成的面积，即特征响度N′(z)在Bark域的积分,由于各临界频带下的特征响度N′(z)有较大差异，导致各频带对响度的影响程度不一。因此，在进行响度的主动控制时，可基于临界频带的影响程度，从大到小依次增加控制频段，以实现响度的最优控制。

2.3 基于CEEMD分解与重构的声品质分析

由回归分析可知，除响度外，其余各客观参量对声品质均有不同程度的影响，其中粗糙度与声品质也呈显著相关性，若只以影响程度最大的响度作为控制变量进行声品质的主动控制，可能会出现响度最优控制而非声品质最优控制的情况，因此需进一步探索声品质的最佳控制策略。

以粗糙度为例，计算公式见式(4)，其中,R为粗糙度，fmod为调制频率，ΔLE为掩蔽深度[11]，可以看出其计算方式与响度具有较大的不同，所以无法从计算公式推导出各客观参量之间的关系，进而确定控制频段。主动控制的目的是人为地控制次级声源消除噪声中令人烦躁的频率成分，因此为探索噪声中各频段对声品质的影响，可通过对原信号进行分解重构，即首先将信号分解为若干分量，然后在重构时依次剔除某些分量，对比声品质的变化情况。

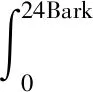
(4)

常用的信号分解重构方法有滤波、小波分析、经验模态分解(Empirical Mode Decomposition， EMD)等，其中滤波和小波分析需提前设置基函数，无法根据原信号特征进行分解，且重构信号中各分量的边界频率容易产生突变，引入的干扰频率较多，而EMD可直接根据原信号自有特征，将其分解成多个本征模态函数IMF分量，具有很高的信噪比和良好的时频聚焦性[12]。但为避免EMD实际应用中出现的模态混叠现象，NE.Huang等人在原信号中引入了高斯白噪声提出CEEMD[13]，步骤如下：

① 基于原信号S，按照公式(5)引入n组高斯白噪声Ga，每组需正负成对，N1、N2即为处理后的信号，共计2n组信号x2n(t)，

(5)

② 三次样条插值拟合，形成xi(t)上、下包络线；

③ 求解包络线均值mi1(t)，并计算新序列hi1(t)=xi(t)-mi1(t)；

④ 判断hi1(t)是否满足条件：

i.|V极点数-V零点数|≤1，

ii.上、下包络线关于时间轴局部对称；

⑤ 若满足步骤(4)，以xi(t)-mi1(t)为原始信号，重复上述步骤，得到k个IMF分量；

⑥ 当迭代到无法继续分解出IMF分量时，记此时的残余信号为ri(t)；

⑦ 求xi(t)第j阶分量均值，得到原信号S第j阶IMF分量cj，公式见式(6)：

(6)

⑧ 完成CEEMD分解，原信号S可由公式(7)表示，其中x(t)为原序列，r(t)为残余信号序列:

(7)

按照上述步骤，基于MATLAB对52号样本信号进行CEEMD分解，结果如图5所示，原信号S被分解为15个IMF分量以及1个残差余量，可由公式(8)表示，其中Res是分解后的参与信号。由图可知，第6阶至第11阶噪声幅值较大，其余各阶幅值较小，对比各分量的波形可以看出，所得的IMF分量之间无明显的模态混叠，证明了采用CEEMD对信号分解的正确性。

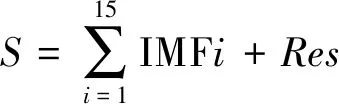
(8)

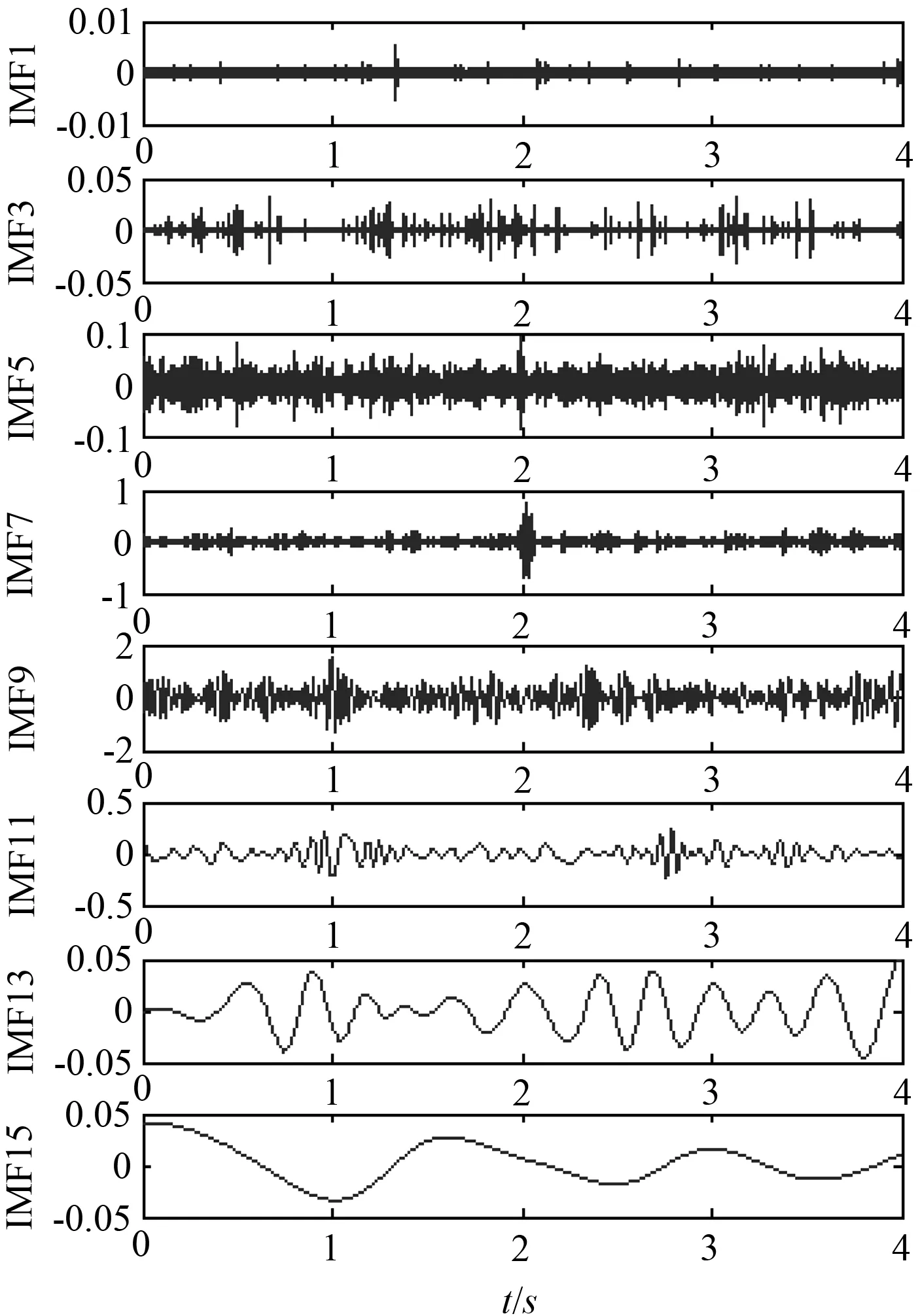
图5 52号样本的CEEMD分解

为确定各IMF分量对声品质的影响，可对IMF分量进行求和重构，在重构过程中依次剔除某分量得到重构信号S-IMFi，计算重构信号的客观参量，并利用LS-SVM模型预测得到烦躁度等级，根据其值变化确定各IMF分量对声品质的影响程度。

按照上述思路，首先对IMF分量进行FFT分析，确定对应的频率范围，然后依次剔除IMF分量进行重构，并求得重构信号的烦躁度等级，结果如表4所示。由表可以看出，对声品质影响最大的为IMF6分量，对应的频率范围为378～1 044 Hz，重构信号S-IMF6烦躁度等级降低了18.0 %。为更直观地表征基于CEEMD分解得到的IMF分量对声品质的影响程度，定义一个新的参数，即影响因子FCEEMD-SQ，计算公式见式(9)。

表4 基于CEEMD分解的重构信号的加权参数

(9)

式中，SQ(S)表示原信号烦躁度等级，SQ(S-IMFi)表示剔除第i阶IMF分量后的重构信号的烦躁度等级.以IMF6分量为例，其影响因子FCEEMD-SQ=0.180，在进行声品质主动控制时，即可依据影响因子FCEEMD-SQ寻找声品质的最优控制频段。

3 声品质主动控制

3.1 FELMS算法

LMS(Least Mean Square)是自适应控制系统中较为常用的时域迭代算法，它能将误差实时反馈至系统中，使系统能够自适应迭代调整输出进而保持误差值的均方最小。研究人员在将其应用于噪声主动控制中时，为了消除次级通道时延对控制效果的影响，形成了FXLMS(Filter-X Least Mean Square)算法，在此基础上发展而来的ANC系统如图6(a)所示，主要用于以声压级为控制目标的主动降噪中。在此基础上，KUO为了实现对特定频率的噪声进行选择性控制，在次级通道以及误差反馈通道增加了滤波器Hw(Z)，发展出了适用于声品质主动控制的FELMS算法[14]，通过调节残差滤波器Hw(Z)的通带进行选择性抵消，重塑噪声频谱，实现声品的主动控制，基于FELMS算法的ANC系统如图6(b)所示。

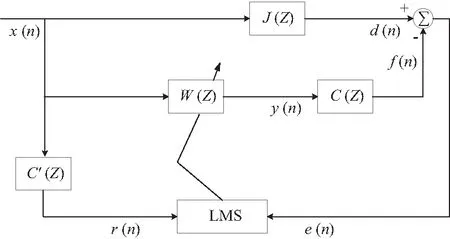
(a) 基于FXLMS算法的ANC系统

上图中，W(Z)为FIR(Finite Impulse Response)自适应滤波器，权系数由LMS算法根据主动降噪目标区域反馈的残差进行实时更新，LMS迭代公式如下：

W(n+1)=W(n)+2μe(n)x(n)，

(10)

式中：W(n+1)为n+1时刻权系数;W(n)为n时刻的全系数;μ为收敛因子;e(n)为残差信号;x(n)为参考信号。FXLMS算法由于增加了C′(Z)，迭代公式见式(11)，其中r(n)为参考信号X(n)与C′(Z)的卷积。

W(n+1)=W(n)-2μe(n)r(n)，

(11)

基于式(11)，FELMS算法中W(Z)的计算如式(12)所示，其中eh(n)、rh(n)为e(n)、r(n)经过Hw(Z)滤波后的信号，LMS算法以此作为输入进行运算，不断调整滤波器权系数，使目标区域始终保持被控频段声压的均方最小，以达到最佳的主动控制效果。在Matlab Simulink中建立基于FELMS算法的ANC系统，其中残差滤波器选取可设计出任意幅频响应曲线的FIR2型滤波器。

W(n+1)=W(n)-2μeh(n)rh(n)。

(12)

相关研究表明，FELMS算法的收敛性能受被控频段范围的影响，成反比关系，即被控频段范围越小，收敛性能越好，被控频段的控制效果越好，反之，被控频段范围越大，收敛性能越差，稳定后的误差均方值就越大[15-16]。因此在进行声品质客观参量主动控制时，应根据各频段对被控参量的影响程度，优先控制影响最大的频段，然后按照影响程度的大小依次增加被控频段，进而寻找出被控参量的最优控制频段。

3.2 基于响度的声品质主动控制

将52号样本的24个特征响度按照其值从大到小排序，如表5所示，按照序号依次增加被控制的临界频带个数，设置残差滤波器的通带，然后基于MATLAB Simulink模型进行仿真，共计24组。

表5 52号样本特征响度排序表

计算每组仿真后噪声的声品质客观参量，响度随被控临界频带的变化如图7所示，因优先控制的12个临界频带特征响度较大，此时响度控制效果明显，响度随被控频带个数增加而降低.但此后控制的临界频带不仅特征响度较小，而且对应的频率范围逐渐增宽，响度的控制效果随着被控频率范围的增加逐渐变差，因此响度随被控临界频带个数的增加而升高。由图可知，控制后的响度值随被控的临界频带个数呈先降后增的趋势，当被控制的频带为Bark1～Bark12，对应频率为20～1 720 Hz时，响度的控制达到最优，由16.3sone下降至10.8sone，取得了33.7 %的降幅。图8为响度达到最优时的特征响度曲线，可以看出被控制的Bark1～Bark12的特征响度均取得了良好的控制效果。

图7 被控临界频带个数对响度控制效果的影响

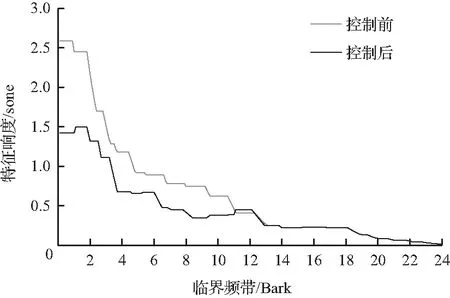
图8 控制前后特征响度曲线

将52号样本响度达到最优控制时的声品质客观参量输入LS-SVM声品质预测模型，得到的烦躁度等级如表6所示，可以看出，控制后除尖锐度因高频占比相对增加导致其略有升高外，其余客观参量均有不同程度的降低，最终烦躁度下降了2.39个等级，降幅为25.8 %。

表6 响度最优控制时客观参量及声品质的变化

3.3 基于FCEEMD-SQ的声品质主动控制

由上文的分析可知，响度最优并不等于声品质最优，因此为进一步提升声品质的控制效果，基于所提出的新参数影响因子FCEEMD-SQ进行主动控制仿真，然后与响度最优声品质的改善情况进行对比，进而确定声品质最佳的主动控制频段。

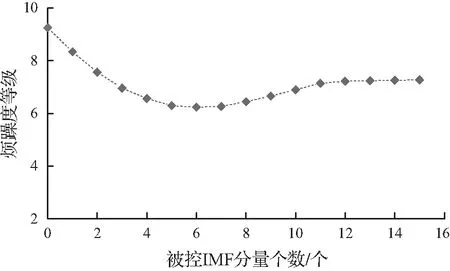
图9 烦躁度等级与被控IMF分量个数的变化关系

与寻找响度最优控制频段相似，依据表4中各IMF分量的影响因子FCEEMD-SQ，从大到小依次增加被控频段进行主动控制仿真，共计15组，计算每组仿真后的客观参量，并利用所建LS-SVM模型进行预测，声品质随被控IMF分量个数的变化如图9所示。由图可知，当被控IMF分量个数小于6时，烦躁度等级随着被控分量个数的增加而降低；当被控IMF分量个数大于6时，声品质控制效果随着被控频率范围的增加逐渐变差；当被控IMF分量个数等于6时，即被控频段为21～2 245 Hz时，声品质的控制达到最优，由控制前的9.25下降至控制后的6.23。

图10显示了声品质最优控制时，在仿真过程中影响声品质的两个主要客观参量响度、粗糙度的时域变化曲线，可以看出所建立噪声主动控制系统具有良好的收敛性，在大约经过0.3秒收敛至稳定状态，响度由控制前的16.3 sone下降至11.0 sone，粗糙度由控制前的1.76 asper下降至1.22 asper。

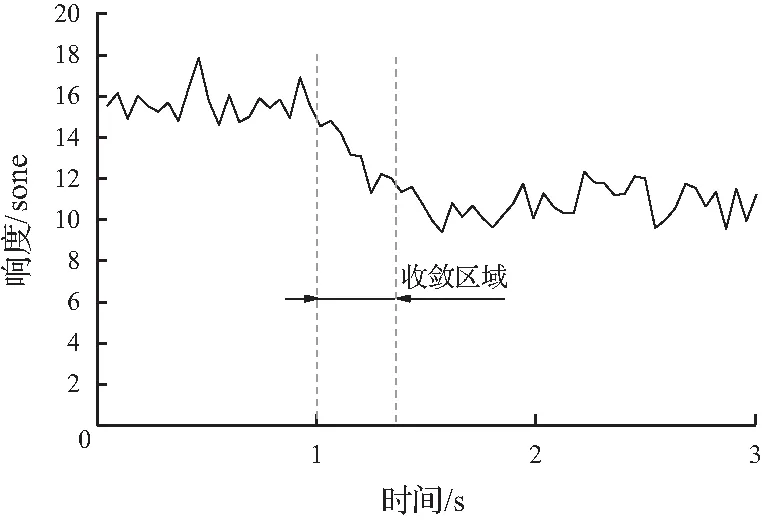
(a) 响度时域变化曲线

表7显示了基于响度及影响因子FCEEMD-SQ两种方法最优控制时的客观参量及烦躁度等级，由表可知，相较于响度最优控制，当基于FCEEMD-SQ控制声品质达到最优时，虽响度略有上升，但粗糙度却进一步降低了0.15asper，最终的烦躁度又降低了0.63个等级，声品质控制效果提升了6.8 %，说明了基于响度单一参量进行声品质主动控制的局限性以及基于所提参数FCEEMD-SQ进行声品质主动控制的正确性。

表7 最优控制时客观参量及声品质的变化

为进一步验证主动控制后声品质的改善情况，组织原主观评审团对控制后的噪声进行主观评价，结果如图11所示，控制前后声品质变化情况与LS-SVM预测结果基本一致，再次证明了所建立的预测模型具有较高的精度，当声品质最优控制时，主观烦躁度等级由控制前的9.28下降至控制后的6.21，下降幅度为33.1 %，极大地改善了车内声品质。

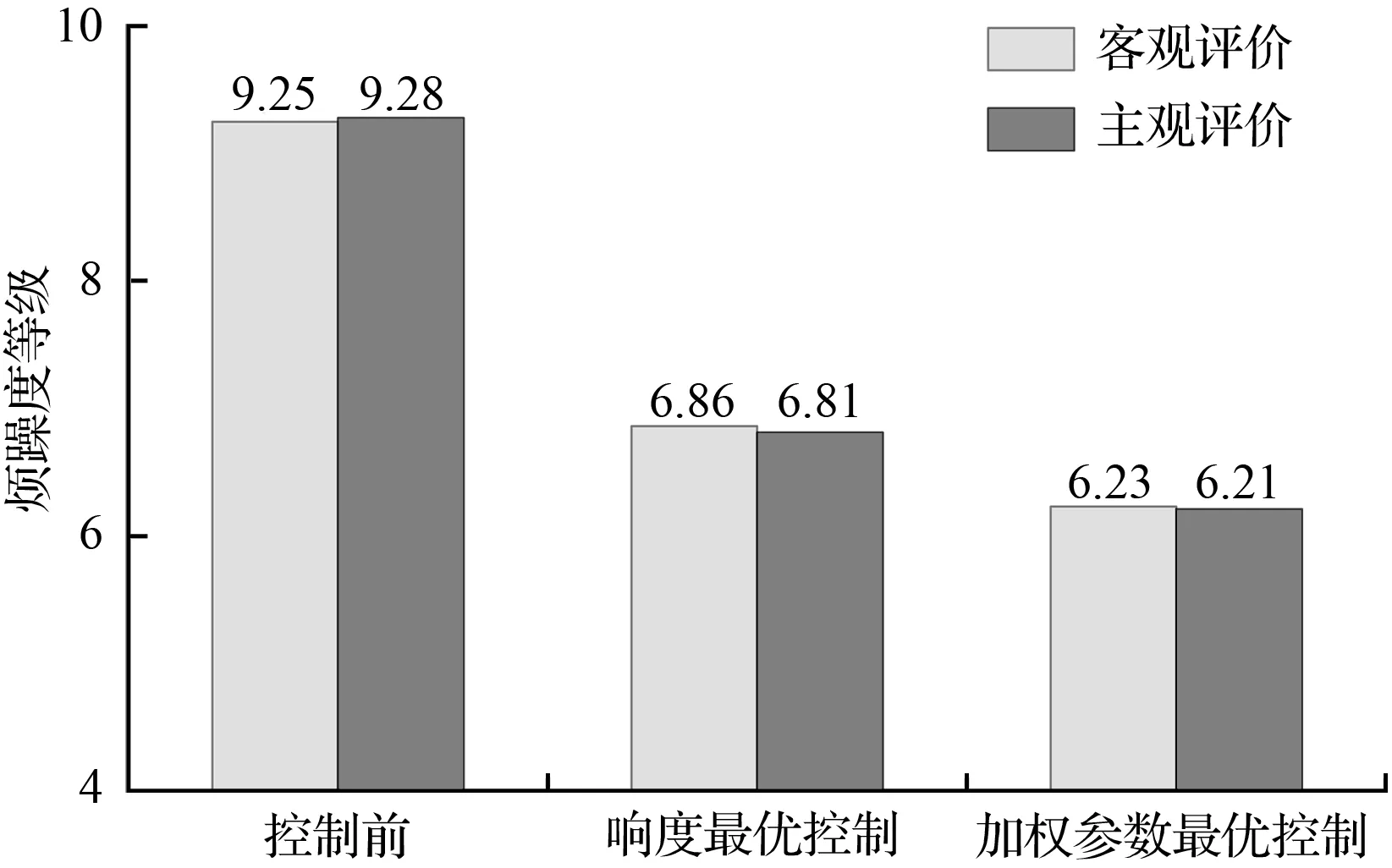
图11 控制前后主客观声品质变化

4 结论

基于FELMS算法的噪声主动控制系统结构简单，收敛性及稳定性均较好，具有较高的工程应用价值且前景广泛，在此背景下，本文以影响汽车舒适度的车内噪声为研究对象，建立了预测模型，实现了声品质的客观评价，提出了在考虑控制频段范围大小对自适应滤波性能影响的情况下，实现声品质最优主动控制的方法，主要研究成果如下：

① 进行了实车道路噪声采集和声品质主观评价试验，经过数据处理得到了54组样本信号的主观烦躁度等级，并计算得到声品质客观参量，建立了高精度的LS-SVM预测模型，平均预测误差仅为3.61 %，实现了声品质的客观评价；

② 引入高斯白噪声优化EMD，基于CEEMD分解重构，提出了用于表征IMF分量对声品质影响程度的新参数影响因子FCEEMD-SQ，为寻找声品质最优控制频段提供了理论依据；

③ 考虑到频率范围对自适应滤波性能的影响，提出了寻找声品质最优控制频段的方法，进行了多次仿真及二次主客观声品质评价，结果表明，基于FCEEMD-SQ的声品质控制效果优于基于响度的控制方法，当声品质达到最佳控制时，主观烦躁度下降了3.07个等级，车内噪声由烦躁下降至有点烦躁，大幅改善了车内噪声声品质，提升了驾驶及乘坐舒适性。