基于Karhunen-Loève级数的改进摄动随机有限元法

2021-04-13李秀梅邵湛钧李朝阳张永兵

广西大学学报（自然科学版） 2021年1期

李秀梅，邵湛钧，李朝阳，张永兵

(广西大学土木建筑工程学院，广西南宁 530004)

0 引言

对具有随机参数的结构进行分析，获得其位移与可靠度等数据[1-2]，对于提高结构分析的精度与可信度是非常有意义的，因此随机分析是非常重要的。

在随机分析中，结构的随机性往往表现为连续的随机场函数，而随机有限元法的计算对象是随机变量，因此随机场需要被离散成若干随机变量，所以真正的随机有限元必须包含随机场的离散[3]。Karhunen-Loève(简称K-L)级数展开法数学格式严谨明确，且对随机场离散高效便捷，已被广泛地应用。黄炎生等[4]将K-L法与Neumann法进行了结合，杨绿峰等[5]将K-L法与预处理谱随机有限元法进行结合，TSABTILI等[6]推导了Spartan空间随机场的K-L展开式，ZHENG等[7]建立了统一的n维随机场K-L展开式，MONTOYA等[8]提出了一种在随机场参数稀少的情况下模拟非平稳高斯随机场与非高斯随机场的新方法。

摄动随机有限元法有着清晰的理论证明，在处理小变异随机结构时得到的结果精度较高，非常适合工程随机分析。因此，近些年来学者们对摄动随机有限元法进行诸多改进。KAMINSKI[9]将广义随机摄动技术与边界元法、有限元法和有限差分法进行了结合。WANG等[10]针对大变异非线性结构的动力问题提出了一种基于摄动随机有限元法的新算法。WU等[11]结合模态方法、二阶摄动技术与数值理论方法，从一阶精度的角度建立了有限元模型的近似随机模型。廖光明等[12]提出了线弹性结构的n阶摄动随机有限元法。QIU等[13]针对特征值问题，考虑设计变量的不确定性，提出了一种改进的随机摄动法。

WU等[11]针对摄动随机有限元法需要对系统矩阵求导、大变异情况下精度低的缺点进行了改进，提出了改进的摄动随机有限元法(MPSFEM)。该方法对比传统方法最大的优势在于无需对系统矩阵进行求导，在计算复杂问题时可以省略大量的计算过程，且计算精度高，在只有一个随机变量的情况下，结果甚至可以达到五阶精度。文献[14]已经证明MPSFEM在处理静力弹性问题、框架结构特征值问题、桁架非线性问题以及热传导问题时比摄动随机有限元法更具优势，文献[15]表明改进的摄动法在处理双曲型热传导问题时比传统摄动法更有效，文献[16]提出了基于框架结构极限塑性分析QR法的MPSM-QR法。但以上研究大多将随机参数视为单一随机变量，并未引入随机场理论。

本文系统地阐述了一维到多维随机场的K-L展开，并将其与MPSFEM进行结合，建立了基于Karhunen-Loève级数的改进摄动随机有限元法(简称KLSMPSFEM)，并对多维随机场下的结构进行随机分析，以基于Karhunen-Loève级数的蒙特卡洛有限元法[17](简称MCM)的解作为参考解，同时对比基于Karhunen-Loève级数的摄动随机有限元法(简称PSM)，讨论3种方法精度与效率的不同之处，以此来阐述该算法的优势。

1 随机场的K-L级数展开

1.1 一维随机场的K-L展开

K-L法将随机场离散成一个均值随机场与一个零均值随机场之和，如式(1)

(1)

随机场的协方差函数为C(x1,x2)，由Fourier级数展开定理可知

(2)

其中:λi为协方差函数特征值;fi(x)为协方差函数的特征函数，它们可以通过求解第二类Fredholm积分方程来获得，即

(3)

其中:D为随机场区域。

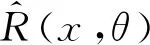
(4)

式中:ξi(θ)是一组不相关的标准正态分布随机向量。

在实际应用时，通常截取有限项级数来近似代替上式，则可得到随机场的K-L级数展开为

(5)

K-L级数展开法将随机场离散成一组不相关的随机变量，与局部平均法等相比，该方法只需要较少的随机变量就能较好地模拟随机场，提高了计算效率。

1.2 多维随机场的K-L展开

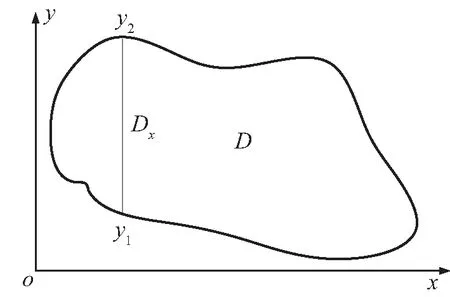
图1 形状不规则的二维随机场

对于二维随机场，假设有一零均值随机场R(x,y,θ)如图1所示，其随机场区域为D，协方差函数为C(x1,x2;y1,y2)，要将此随机场进行K-L展开，需要先固定坐标x的位置，其协方差函数变为准一维协方差函数C(x;y1,y2)，则该随机场的K-L展开为

(6)

λi(x)与fi(x,y)为协方差函数C(x;y1,y2)的特征值与特征函数，求解下式即可得到

(7)

其中:Dx如图1所示。

若将二维随机场按式(6)表示，则还需要将中间一维随机过程ξi(x,θ)进行K-L分解，假设其协方差函数为K(x1,x2)，则该随机过程K-L展开式为

(8)

其中:γij(θ)为一组互不相关的标准正态分布随机变量;φij与gij(x)为协方差函数K(x1,x2)的特征值与特征函数，可通过下式求解

(9)

因此，二维随机场可分解为

(10)

若将此推广到三维随机场，则其K-L展开式为

(11)

其中：qijk(x)、gij(x,y)、fi(x,y,z)与ηijk、φij(x)、λi(x,y)分别为一维、二维、三维协方差函数的特征函数与特征值;γijk(θ)为一组互不相关的标准正态分布随机变量。

以上为多维随机场K-L展开的统一计算格式，该方法将一个n维随机场分解为n个一维随机过程，每个随机过程都可以用一维随机场的K-L展开式进行展开，其计算难点在于计算中间一维随机过程的Fredholm积分方程式，对此ZHENG等[7]给出了一种高效的计算方法对于少数形状规则的二维随机场，其协方差函数可以在两个方向上分离，因此可以使用一维随机场的K-L展开式在2个方向上对其分别进行离散，最后组合成二维随机场协方差函数的特征值与特征函数，具体方法可参考文献[18]。

2 改进的摄动随机有限元法

改进的摄动随机有限元法(MPSFEM)分为随机变量不相关、随机变量不相关且具有对称的联合概率密度函数、随机变量相关3种情况，不同的情况精度有所不同[14]。由于K-L展开所得到的随机变量是一组不相关的标准正态分布随机变量，因此本文采取随机变量不相关且具有对称的联合概率密度函数的情况。

在MPSFEM中，随机向量α被替换为确定性向量bi，形式如下

(12)

则MPSFEM的位移四阶泰勒展开式为

(13)

(14)

由式(13)与式(14)相加相减可得

(15)

(16)

其中:

zi=U(bi)+U(-bi)-2U0，

(17)

wi=U(bi)-U(-bi)。

(18)

将zi与wi代入MPSFEM的均值与标准差表达式即可得

(19)

(20)

式中的未知量只有zi与wi，而zi与wi只需要U(±bi)就能求得，因此只需按照下式求U(±bi)即可得

K(±bi)U(±bi)=F。

(21)

3 基于K-L级数的改进摄动随机有限元法

以一维随机场的K-L展开为例，离散后得随机向量ξ(θ) ，即

ξ(θ)=(ξ1(θ),ξ2(θ), …,ξq(θ))，

(22)

其中:每个随机变量均服从标准正态分布，均值为0，标准差为1。

将随机向量ξ(θ)替换为确定性向量

(23)

然后按照MPSFEM计算格式进行计算即可。KLSMPSFEM具体计算步骤如下：

① 获得Fredholm积分方程的解析解、数值解或实验解，得到特征值λi与特征函数fi(x)，从而得到随机向量ξ(θ)，该随机向量包含q个随机变量。

② 将随机向量ξ(θ)按式(23)替换为确定性向量bi，重复q次。

③ 将bi与-bi代入到单元刚度矩阵中进行积分计算，得到Ke(bi)与Ke(-bi)(i为单元编号)，并组装得到结构刚度矩阵K(±bi)。

④ 将K(±bi)代入式(21)得到U(±bi)。

⑤ 将U(±bi)代入式(17)、(18)得到zi与wi。

⑥ 将zi与wi代入式(19)、(20)求得结构响应的均值与方差。

以上就是KLSMPSFEM的具体计算步骤。本算法将K-L法与MPSFEM法进行了结合，使其可以处理随机场条件下的各类随机问题，且由于K-L法将随机场直接离散为一系列不相关的随机变量，因此该算法无需进行MPSFEM中的相关随机变量转换步骤，也无需判断随机变量的概率密度函数，直接进行计算即可，节省了大量的时间。

4 算例分析

例1：设有一根二维随机场下的悬臂深梁，如图2所示，其相应的结构参数如下：

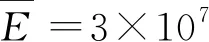
Cov(x1,x2;y1,y2)=σ2e-|x1-x2|/40-|y1-y2|/5。

图2 二维随机场下的悬臂深梁

首先对随机场进行离散，图3列出了K-L法模拟该随机场得到的前20阶特征函数与特征值的逐级叠加，可以看到随着阶数的增加，图像变化逐渐变小。从第16阶开始，图像趋于稳定，因此本题取q=16。

(a) 前4阶叠加

图4 前16阶特征函数与特征值的叠加

图4给出了前16阶的特征函数与特征值叠加后的三维图。在题目中，随机场x方向相关长度取为40 cm，等于结构的在该方向的长度，y方向相关长度取为5 cm，等于结构的在该方向的长度的一半，而由图3与图4可知，在进行了16阶叠加后，随机场在x方向上变化幅度较小，而在y方向上变化剧烈，这说明在相关长度较大的情况下，特征值衰减快，取较少的阶数就能较好地模拟随机场，相关长度较小则特征值衰减慢，需要取较多的阶数才能较好地模拟随机场，因此阶数的选取取决于相关长度较小的方向。

本题计算采用4节点等参元，MCM样本数量取10 000个，得到的计算结果如图5所示。

在精度方面，当变异系数在0.05至0.15之间时，以MCM为计算基准，3种方法精度相差不大；当变异系数在0.15至0.25之间时，KLSMPSFEM的计算精度要明显高于PSM，在计算结构响应标准差时，精度差异更加明显。

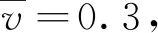
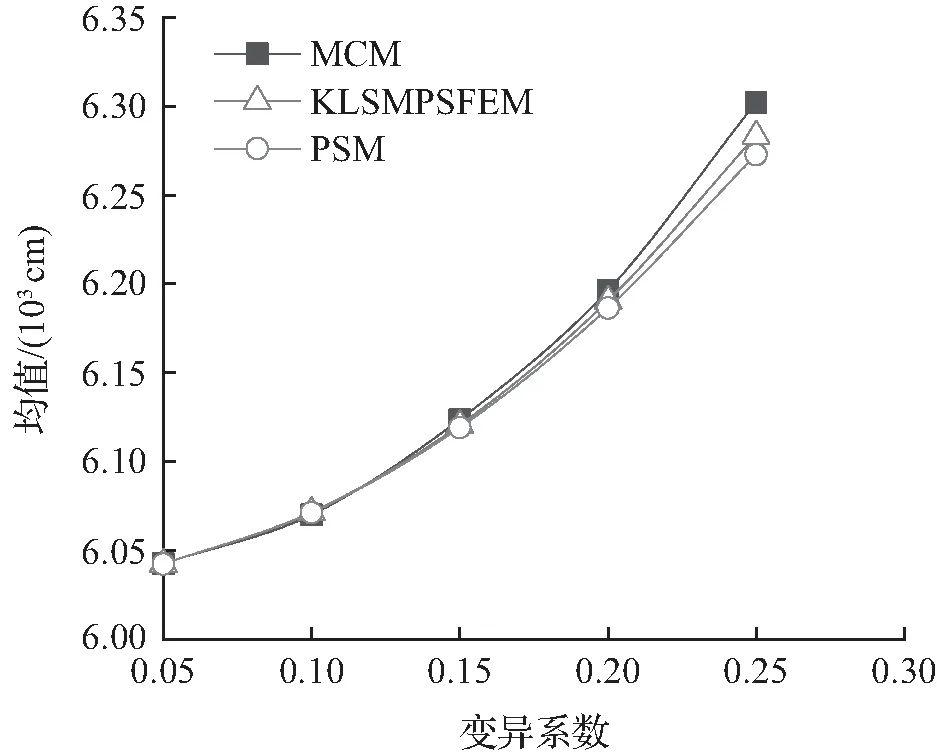
(a) 均值

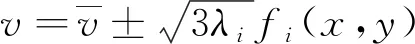
(24)

图6为不同方法计算A点竖向位移得到的二阶估计值，由图6可知，KLSMPSFEM的计算结果与MCM的拟合度很高，符合算例1得出的结论。

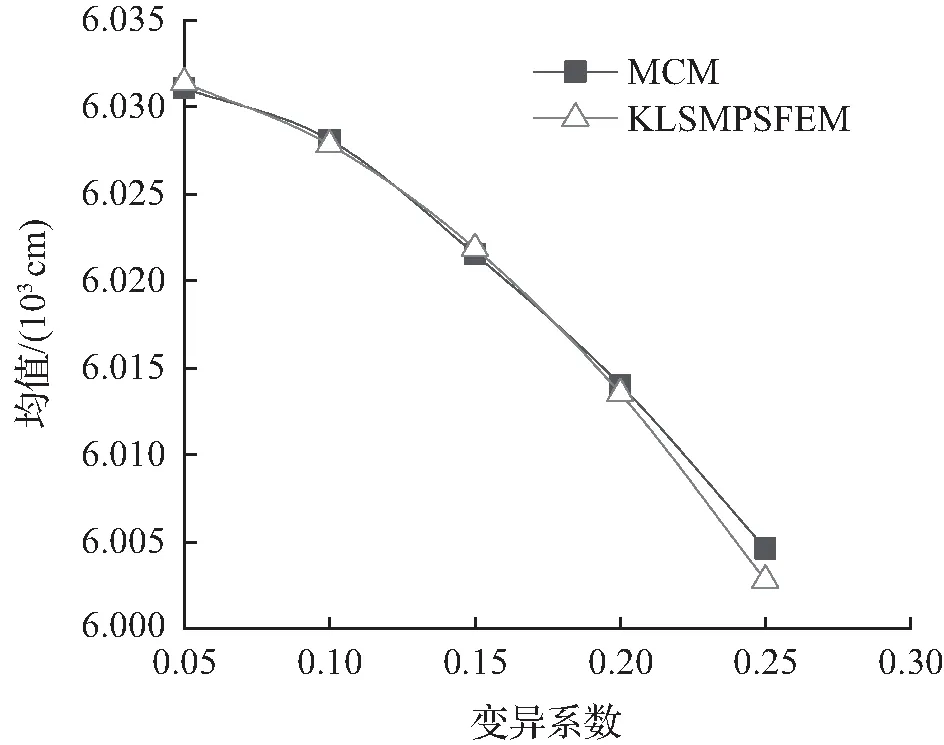
(a) 均值

在效率方面，使用MCM需要抓取样本并计算，算例中抓取10 000个样本就需要计算10 000次，耗费了大量的计算时间，使用PSM需要进行刚度矩阵求导的字符运算，耗费了大量的编程时间，而使用KLSMPSFEM则只需计算1次，也不涉及任何字符运算，程序编写方便，运算速度快，因此KLSMPSFEM的效率无疑是最高的。