基于加权块稀疏联合非凸低秩约束的高光谱图像去条带方法

袁宇丽，吕俊瑞，罗学刚,3,4

（1.内江师范学院 计算机科学学院，四川 内江 641100；2.攀枝花学院 数学与计算机学院，四川 攀枝花 617000；3.四川旅游学院 信息与工程学院，四川 成都 610100；4.电子科技大学 信息与通信工程学院，四川 成都 610054）

引言

条带噪声是星载和机载多探条带测器光谱仪图像中常见的结构噪声。高光谱成像传感器在成像过程中不可避免地会对采集到的HSI 数据产生条带噪声。HSI 中的条带噪声将严重影响高光谱图像的视觉质量，对混解、图像融合、目标检测、分类等后续处理提出了很大的挑战[1]。为了获得更好的视觉质量，提高HSI 后续应用的能力，去除HSI 中的条带噪声是一个重要研究课题。针对去条带的问题，学者们提出了众多模型[1-5]。其中，基于全变分模型[6-8]的图像分离方法实现HSI 条带噪声去除效果良好，受到学者们的广泛关注，但在实际应用中依然存在结构细节丢失等不足。为了增强去噪适应性，大量改进的方法先后被提出。2016 年Bouali 等人提出了一种自适应单向变分的HSI 条带去除（unidirectional total variation, UTV）[7]模型，该方法利用方向TV 刻画条带结构，分离条带效果良好，但对于无条带区域的识别不够准确，特别是对严重条带噪声的识别性能较差；Dou 等人在2018 年提出基于方向ℓ0范数稀疏约束的去条带噪声模型[9]，采用方向ℓ0范数的正则化来描述条带全局稀疏分布，但全局稀疏度不能反映条带分量的内部结构，当条带稠密时导致条带稀疏性失效；2019 年Wang等人提出RBSD（ reweighted block sparsity destriping, RBSD）去条带模型[10]，利用加权块稀疏和UTV 正则化约束提高图像变化区域的局部平滑度，由于该模型没有考虑高光谱影像的光谱特征，性能仍有较大的提升空间；Liu 等人[11]在2019 年提出基于小波域的低秩组稀疏去条带模型（ wavelet-domain low-rank/group-sparse destriping,WLRGSD），在变换域下的低秩稀疏约束分离条带，效果良好，但条带和图像结构在小波域中都处于高频区域，不能较好地辨识容易导致图像模糊；2020 年Yang 等人[12]提出联合单向变分和非凸低秩构建（TV and nonconvex low-rank, TVNLR）去条带模型，利用高阶变分较好地自适应图像结构，但没有考虑条带分量结构特点和高光谱影像光谱特征，容易引起非周期条带分离不完全的缺陷。

为了避免条带噪声去除过程中丢失影像细节，本文提出一种基于加权块稀疏联合最小最大非凸惩罚约束的HSI 条带噪声去除方法（WBS-MCP）。WBS-MCP 在保持影像边缘和加强区域平滑性方面具有良好的优势，特别是对于非周期条带噪声去除获得了更好的效果。

1 WBS-MCP 模型及优化求解

本节首先描述条带噪声模型，然后介绍MCP函数和WBS-MCP 模型及优化求解过程，最后描述算法流程。

1.1 条带噪声描述

设定遥感高光谱图像为Y∈RM×N×B，空间大小为M×N（M为宽度，N为高度），光谱波段数为B，将HSI 条带效应建模为加性噪声，模型建立如（1）式：

其中：Y表示含噪HSI 图像；X表示无噪声的HSI 图像；S表示条带噪声；Y、X和S具有相同维数，大小为M×N×B。HSI 条带噪声去除就是从观测噪声图像中还原出具有图像本身特征潜在影像X。为了更好地描述条带噪声的低秩和稀疏性，以图像块为单位将HSI 数据从沿条带垂直方向和光谱方向利用滑动窗口分解构建图像矩阵，描述形式如（2）式：

式中Y、X和S分别表示HSI 影像按图像块分组排列的观测图像矩阵、干净图像矩阵和条带噪声矩阵。

1.2 MCP 惩罚

UTV[7]对图像梯度利用ℓ1范数进行约束，体现条带噪声的稀疏性特征。研究发现ℓ0范数为最佳描述稀疏性，然而由于ℓ0范数求解困难，采用ℓ1范数和核范数等凸函数近似描述低秩和稀疏，获得近似ℓ0范数的效果。在图像恢复中，非凸惩罚通常比凸近似逼近具有更好的性能，能更加准确描述低秩和稀疏。因此，非凸惩罚函数广泛应用在描述低秩和稀疏的应用中，其中常见的有bridge[13]、capped-ℓ1[14]、平滑剪切绝对偏差（SCAD）[15]和极小极大非凸惩罚（MCP）[16]。文献[17]对上述约束函数在图像恢复中进行数值实验比较，发现MCP 模型在效率和精度上均优于经典的TV 模型，性能比其他几种惩罚函数表现得更突出[17]。

对于一维变量t, MCP 标量函数定义如（3）式[17]：

式中 α＞0 和 β≥1分别为两个常数。

扩展到二维矩阵K∈Rp×q， MCP 函数定义为其中σi(K)表示矩阵K的SVD 奇异值,r表示秩。

那么，相应的MCP 阈值操作算子可表示为

图1 为ℓ0、ℓ1和MCP 3 种惩罚函数的阈值示意图。从图中可以发现，MCP 函数具有连续性、稀疏性和无偏性等特征，保证MCP 正则化问题具有良好的统计性质, 表示非凸稀疏恢复MCP 模型比凸稀疏恢复模型具有更好的性能。由于MCP 函数具有良好的性质，MCP 函数已经在稳健主成分分析问题上成功应用。

图1 3 种惩罚函数的阈值示意图Fig.1 Threshold schematic of 3 penalty functions

1.3 WBS-MCP 模型描述

本节描述一种将MCP 约束和加权ℓ2,1范数融入到UTV 模型中，联合空间-光谱下条带低秩性和稀疏性正则化项的去条带新模型WBS-MCP：

其中：λ1、λ2、λ3为非负参数；||S||w,2,1表示加权ℓ2,1范数，定义为和分别表示水平和垂直方向的微分算子。（5）式的第1 项和第2 项分别描述条带噪声低秩性和稀疏性约束，第3 项为估计图像水平方向的TV 正则化项。图2 详细地描述了WBS-MCP 去条带模型。

1.4 模型优化求解

WBS-MCP 模型将（5）式分解为多个子问题采用ADMM 算法迭代求解，通过引入两个辅助变量Q=ΔyS,D=ΔxX，（5）式可以重写为

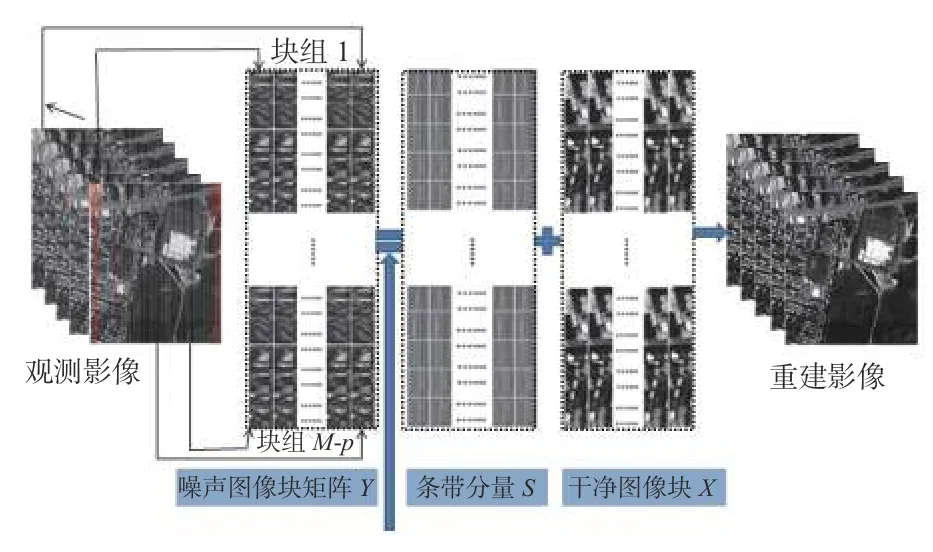
图2 WBS-MCP 去条带模型Fig.2 Stripe removal model of WBS-MCP

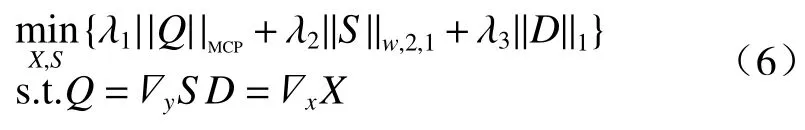
由于模型中目标函数的4 个变量具有可分性，采用增广拉格朗日函数可重写为

其中：G1、G2分别为与约束的拉格朗日乘数； ρ为惩罚参数。

将WBS-MCP 模型的复杂多变量问题简化为多个子问题求解，下面描述分解的子问题第k+1 次迭代求解流程。

1） 估计图像Xk+1子问题，求解可以描述为一个典型的最小二乘模型：

通过对X一阶求导，等价于线性方程组：

式中f ft和f ft−1分别为快速傅里叶变换和逆变换。

2） 条带分量Sk+1子问题，条带分量S可描述为

根据文献[10]的加权ℓ2,1范数最小化问题求解，定义矩阵元素的软阈值操作符算子可求解S为

3） 变量Qk+1子问题求解，可以描述为

4） 变量Dk+1子问题求解，可以描述为

是典型的ℓ1范数最小化问题。对ℓ1范数最小化问题使用矩阵软阈值操作符求解，其闭式解为

式中s hrink(l,τ)=sign(l)×max(|l|−τ,0)。

式中 κ1和κ2为收缩参数。

结合上述已解决的子问题，采用多步迭代求解，直到满足收敛条件结束迭代循环， δ为设定的误差参数。

2 实验结果与分析

为了验证WBS-MCP 模型的有效性，分别对仿真高光谱图像和真实带条带的高光谱图像去除条带，并与UTV[7]、RBSD[10]、WLRGSD[11]和TVNLR[12]4 种性能表现较好的去条带方法对比，结合视觉效果、平均峰值信噪比(MPSNR)、平均特征结构相似性因子(MFSIM)[18]、平均等效视数(ENL)[6]和边缘保持指数(EPI)[6]多种客观评价方法以及谱线曲线综合评价实验结果。实验测试环境为Matlab2015a，计算机硬件参数为Intel(R)Core(TM)i5-2520M CPU @2.5, RAM: 8.00 GB。

2.1 仿真数据实验

模拟实验中，选用了HYDICE Urban 数据集[6]和Washington DC Mall 高光谱图像集[9]作为实验数据源进行周期性和非周期性条带降噪处理。为保证实验比较的公平性，对于给定的实验数据，每种对比方法中的参数保持一致。

2.1.1 周期性条带实验

图3 多种算法对HYDICE Urban 数据集的band5 模拟仿真去条带复原图像视觉效果Fig.3 Restoration results of multiple algorithms using band 5 of HYDICE Urban data set

选取HYDICE Urban 数据集做实验，添加了噪声均值为30、比率为0.25 的周期性条带进行性能比较。图3 和图4 分别为HYDICE Urban 数据集波段5 的多种算法视觉效果图。从图3（c）～图3（e）中可以发现，在垂直方向依然存在比较明显的条带信息，主要原因是选取波段影像结构突出，导致UTV 识别条带区域不够准确，RBSD 在图像变化区域的局部平滑效果不佳和WLRGSD 在影像细节区域引起影像模糊，图3（f）的TVNLR 方法采用了非凸低秩近似，整体图像结构视觉效果较好，采用高阶方向TV 对效果有一定提高，但由于图像内容丰富，无法准确描述存在局部细节丢失，而本文算法采用的自适应加权可以较好地适应图像内容变化较大的情况。

图4 多种算法对HYDICE Urban 数据集的band5 模拟仿真去条带分量分离视觉效果Fig.4 Component results of multiple algorithms using band 5 of HYDICE Urban data set

表1 为在Washington DC Mall 高光谱图像集中增加了5 种不同均值和比率的周期性条带，采用不同算法去条带MPSNR 和MSSIM 值对比。表1中粗体表示不同噪声水平下最佳性能结果，从MPSNR 和MSSIM 指标的比较可以看出，RBSD、UTV、WLRGSD 和TVNLR 随着噪声水平增加性能降低较快，特别是当噪声均值从25 变到30 及比率从0.25 变到0.3 时，性能指标值降低近3 dB，而本文算法降低相对较缓慢。整体性能指标比较结果与图4 和图5 的图像质量保持一致，特别是MSSIM指标值在评价图像边缘结构上与图4 的视觉效果基本吻合。本文模型在多种比较方法中获得最高的指标性能值，这是因为本文模型从空域和光谱域联合考虑条带噪声的方向特性、低秩性和结构稀疏性等特点，特别是以波段为单位将影像分割成块组，利用光谱的低秩特征取得更好的去条带性能。

为了清楚地展示影像重建结果，图5 展示了用不同方法估计Washington DC Mall 高光谱图像集20 波段图像的谱特征曲线。如图5（a）所示，由于条带和其他噪声的影响，原始波段图像的谱特征曲线中出现了许多波动。可以观察到，用图5（b）～5（f）所示的不同方法恢复后，参与比较的算法模型在一定程度上抑制了波动，图5（b）～图5（c）的曲线中还存在微小波动，表明图像部分混合噪声去除无效。从谱特征曲线结果表明，本文算法模型得到的恢复曲线明显比其他方法平滑，说明本文算法具有更好的去噪效果。

2.1.2 非周期性条带实验

本实验以Washington DC Mall 高光谱图像部分子图像集为数据源，加入合成的随机分布非周期性条带噪声。图6 为对加入均值为30 和比率为0.2 的随机条带噪声的DC Mall 数据集波段3 的去条带恢复图像视觉效果。

图6 显示各种方法的去条带结果和局部区域放大比较。比较图6（c） ～图6（e）的放大区域可以看出,恢复的影像整体偏暗，有一定的图像模糊。从白色框图区域可较明显发现图6（c）～图6（f）的垂直方向结构信息被当作条带去除，导致了不清晰,而本文算法结果基本和图6（a）保持一致。另外，UTV 方法恢复图像的结构细节丢失，同时可观察到一些残留的条带，与条带方向相同的图像结构被抑制，缺少条带识别能力。从图6（d）～图6（f）也可发现，由于比较方法对图像结构适应性不够，导致有一定的破坏，残留少量条带在影像中。从图6（g）可知，本文算法恢复图像人工痕迹不明显，条带被较好地去除，同时图像结构保留较完整。与RBSD、WLRGSD 和TVNLR 相比，本文算法利用加权的ℓ2,1范数描述非周期条带稀疏性，较好地保持图像结构，在适应图像结构变化方面能力更强。

图7 为不同去噪影像列均值曲线展示，通过列均值曲线反映去条带噪声影像效果，UTV 的跃变整体偏大, RBSD 和WLRGSD 在中间部分处有明显的偏移且条带分量偏差较多，反映出影像整体偏暗、局部区域偏亮。特别是WLRGSD 震荡幅度过高，TVNLR 的列均值曲线也存在一定的震荡偏差，而本文算法的列均值曲线更平滑，使得图像整体亮度和结构保持效果更好。

表1 多种算法对不同噪声水平的周期条带分量去噪MPSNR 和MFSIM 值对比Table 1 Comparison of MPSNR and MFSIM of multiple algorithms with periodic stripe component at different noise levels

图5 对Washington DC Mall 高光谱图像集20 波段图像用各算法估计谱特征曲线对比Fig.5 Comparison of spectral feature curves by multiple algorithms for band 20 of Washington DC Mall

图6 DC Mall 波段3 的非周期条带去条带恢复效果与局部区域放大比较Fig.6 Comparison of stripe removal restoration effect of aperiodic stripe and local area amplification of DC Mall band 3

图7 去噪后影像列均值曲线图Fig.7 Mean value curves of image list after denoising

2.2 真实数据实验

为了说明本文方法的实用性，选取了两幅受到周期噪声和非周期噪声污染的真实高光谱图像集Terra MODIS进行实验[6]，图8 和图9 分别给出了两幅真实高光谱图像集波段8 和波段34 的去条带处理结果。

图8 和图9 分别为真实周期噪声影像和真实非周期噪声影像的去条带视觉效果。从图中不难发现，图8（c）UTV 方法由于识别条带能力不够，在真实影像去除条带时，部分条带依然保留在影像中；RBSD 方法整体效果较好，但由于图像自适应加权调整不够，依然有少量的条带残余没有被去除,同时模糊了部分细节；WLRGSD 和TVNLR方法由于低秩近似忽略了图像结构特征，导致部分重要细节结构信息被丢失，本文算法去除效果较好，主要是在考虑条带低秩和方向特征的同时，还利用MCP 正则化约束保持结构信息，因此

图8 真实周期噪声影像波段8 的去条带视觉效果图Fig.8 Restoration results of multiple algorithms for band 8 of real periodic noise image

本算法的去噪结果在细节和整体结构方面保留较完整。

图9 真实非周期噪声影像波段34 的去条带视觉效果图Fig.9 Restoration results of multiple algorithms for band 34 of real aperiodic noise image

由于图9（a）中图像遭受不均匀细条带干扰，从图9 中可以看出，几种算法去除效果有一定的差异，由于条带分布不均匀，UTV、TVNLR和RBSD 无法适应条带和图像结构变化，在噪声图像中的条带信息被大部分去除，但仍有部分残留被当做图像内容保留。WLRGSD 利用加权低秩组稀疏去除效果较好，由于本文算法采用加权ℓ2,1范数和MCP 范数，对非周期条带噪声去除效果更佳。表2 为高光谱图像客观评价指标对比表。

表2 高光谱图像客观评价指标对比表Table 2 Comparison of objective evaluation indexes of hyperspectral images

表3 记录了本文算法与RBSD、UTV、WLRGSD和TVNLR 4 种算法对两个数据集中的部分波段的运行时间。从表中可以看出，由于本文算法利用了加权块稀疏和MCP 约束，减少了部分计算量，与其他几种算法相比，效率方面依然保持良好。

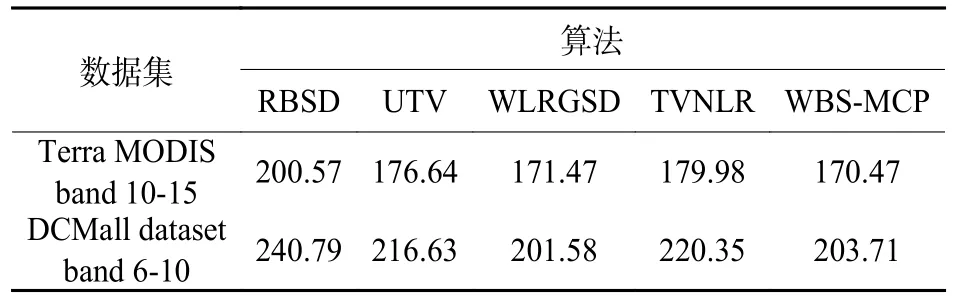
表3 多种算法运行时间对比Table 3 Comparison of running time of various algorithms s

2.3 参数分析

WBS-MCP 模型包含4 个参数:图像块大小p、λ1、λ2、λ3。为了评估和分析这些参数的影响和最优值，本文使用图3 为实验，利用PSNR 值评价测度，采用贪心策略，逐一选取参数值，选4 个参数的最优值。从表4 中不同图像块取值下的PSNR 值对比可以发现，当p取值为7 时，获得最佳的性能，随着图像块加大，性能有一定下降。因此，本文选取p=7。

表4 不同p 值的PSNR 指标值对比Table 4 PSNR comparison of different values of p

图10 绘制了不同正则化参数下λ1、λ2、λ3的PSNR 值实验结果。图10（a）随着λ1从0.001 增加到0.005，PSNR 值有明显的提高，λ1最佳取值在0.005 附近。同理，图10（b）中λ2最佳取值在0.045 附近, 图10（c）中λ3最佳取值在0.002 附近。

图10 不同正则化参数下λ1、λ2、λ3 的PSNR 曲线图Fig.10 PSNR curves of λ1， λ2， λ3 with different regularization parameters

3 结论

本文提出一种针对高光谱图像直条带去除的新模型WBS-MCP。在分析了条带噪声的特点基础上，该模型利用MCP 范数和加权ℓ2，1范数约束，较好地刻画条带低秩特性，同时具有经典UTV正则化项模型，能准确提取图像的主要结构信息，采用自适应的权值优化了图像结构约束，较好地保留估计影像的边缘和纹理结构等信息。通过在模拟数据和真实数据的周期性和非周期条带去除，并采用多种评价指标与同类性能优秀的算法比较，可以看出，WBS-MCP 模型采用了非凸MCP 来表征条带噪声的低秩性，可以有效地将条带分量和图像分离，同时加权ℓ2，1范数约束在图像结构保持方面都优于其他比较方法。将来的工作和研究方向是尝试将旋转策略加入到WBS-MCP 模型中来捕获斜条带。此外，还可以将本方法扩展到视频雨斑去除和红外图像条带噪声去除等应用中。