New structures for closed-form wave solutions for the dynamical equations model related to the ion sound and Langmuir waves
2021-04-12MdNurAlamandOsman
Md Nur Alam and M S Osman
1Department of Mathematics,Pabna University of Science and Technology,Pabna,6600,Bangladesh
2 Department of Mathematics,Faculty of Science,Cairo University,Giza 12613,Egypt
3Department of Mathematics,Faculty of Applied Science,Umm Alqura University,Makkah 21955,Saudi Arabia
Abstract This treatise analyzes the coupled nonlinear system of the model for the ion sound and Langmuir waves.The modified (G ′/G)-expansion procedure is utilized to raise new closed-form wave solutions.Those solutions are investigated through hyperbolic,trigonometric and rational function.The graphical design makes the dynamics of the equations noticeable.It provides the mathematical foundation in diverse sectors of underwater acoustics,electromagnetic wave propagation,design of specific optoelectronic devices and physics quantum mechanics.Herein,we concluded that the studied approach is advanced,meaningful and significant in implementing many solutions of several nonlinear partial differential equations occurring in applied sciences.
Keywords: the modified (G′/G)-expansion method,ion sound wave,Langmuir wave,closed-form wave solutions
1.Introduction
The nonlinear model of the wave equations has evolved to form the physical characteristics of science and engineering [1,2].The nonlinear partial differential equations (NPDEs) have importance in many categories of physical sciences,such as ocean engineering,solid state,geophysics,optics,chemistry,plasma physics,biology,mechanics,material sciences,mathematical physics and mathematics[3–10].The closed-form wave solutions of the NPDEs are a crucial task necessary for understanding the processes and physical phenomena in the diverse applied sciences sectors.Numerous new approaches have been exploited to study this kind of solution for the NPDEs.Some crucial processes include the extended direct algebraic method[11],the sech-tanh technique [12],the sine-Gordon expansion scheme [13,14],the finite series Jacobi elliptic cosine function ansatz [15],the extended tanh expansion method [16],the generalized exponential rational function method [17,18],the improved tan (φ(ξ)/2)-expansion scheme [19,20],the novel(G′/G)-expansion approach[21,22],the extended trial equation method (ETEM) [23],the improved tan (φ(ξ)/2)-expansion method (ITEM) [24],optimal homotopy and the differential transform method [25],the homogeneous balance method [26],the modified Kudryashov method [27],Riccati–Bernoulli sub-ODE method[28],the exp(−φ(ξ))-expansion method[29,30],and the unified method and its generalized form [31–37].
This research deals with the model for Langmuir waves(LWs) and ion sound waves (ISWs) [24,38,39] as below

where the electric field of the Langmuir oscillation and the density perturbation are represented bynd n in the normal form,respectively.Here,we supervise the method of dynamical models concerning the ISW with the effect of the ponderomotive force owing to the high-frequency area,as well as for the LW,which is one variety of nonlinear wave models.The implementation of novel types of soliton solutions for the LW and ISWs has an extremely prominent status through the contributors.A few studies have converged on the Langmuir solitons.Musher et al[40]give support to the application of the weak turbulence hypothesis to LW turbulence,and consideration was given to plasma under relative unmagnetized and magnetized electron and ion temperatures.Zakharov [41] expressed the method of dynamical models for the LW.Benilov [42] illustrated the stability of solitons through the Zakharov model,that recognizes the interaction between ISWs and LWs.In[38,40],a system of equations for the ISW under the action of the ponderomotive force due to the highfrequency field and the LW was discussed.
The main motivation for this work is to study the model for the LWs and ISWs via the modified-expansion method [22,43].The essential advantage of this technique over the other methods in the literature is that it provides novel explicit analytical wave solutions,including many real free parameters.The closed-form wave solutions of nonlinear NPDEs have their significant meaning to reveal the interior device of the physical phenomena.Furthermore,the calculations in this method are very simple and vital to providing new solutions compared to the steps in other approaches.
The synopsis of this paper is shown below.We mention the algorithm of the new method in section 2.The implementation of our approach for solving the solitary wave phenomena of the studied model is manifested and some discussions are provided in section 3.Finally,some outcomes of the research are presented in section 4.
2.A brief description of the modified -expansion scheme
The following strides summarize the modified sion method [22,43].
Suppose an NPDE has the form:
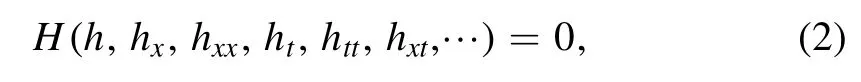
where h=h(x,t) and H is a polynomial in its arguments.Assume that:
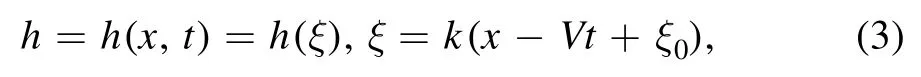
where k,ξ0and V are constants.From equation (2) and equation (3),we get

• Postulation 1:calculate m using the rule of the homogeneous analysis in(4).
• Postulation 2:the modified-expansion technique suggested that

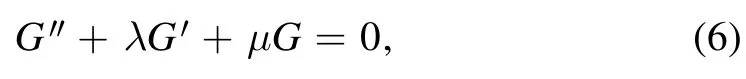
where Ai,λ and μ are free parameters.From (6),we have

• If b >0,then

• If b=0,then

• If b <0,then
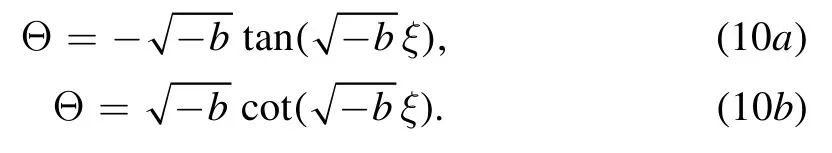
• Postulation 3:inserting(5)and(7)into(4),and collecting all terms with the same order of Θ together,the left-hand side of equation(4)is converted into the polynomial in Θ.Equating each coefficient of this polynomial to zero yields a set of algebraic equations which can be solved to find the values of the unknown parameters.Thus,the general solutions of equation (2) are obtained.
3.Soliton solutions for the model system related to ISWs and LWs
Here,we study the coupled nonlinear system of the model related to ISWs and LWs [24,38,39]:

Let us consider the transformations:
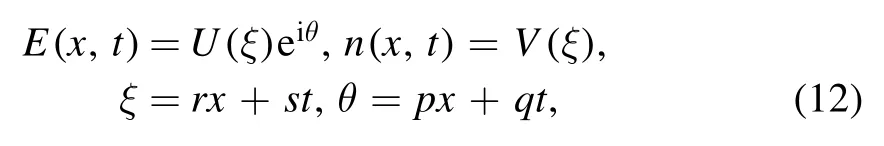
where r,s,p and q are constants.We obtain:

From (13) and by integrating (15) twice w.r.t.ξ,we get:
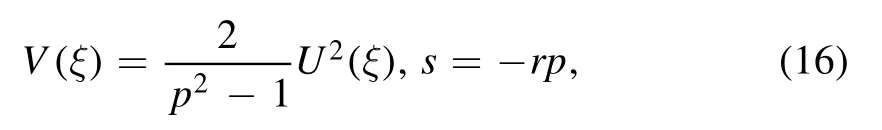
where the integration’s constants are identical zero.Substituting equation (16) into equation (14),we reach:-expan-

Plugging (18) into (17) and by applying postulation 3,we find that:
• Result1:andWe get the following solutions:


• Result 2:A0=0,A1=f1r,and A−1=0.We have:


• Result 3:q=A0=0,A1=f1r,andWe obtain:



• Result 4:q=A0=0,A1=f1r,andWe get:



3.1.Physical and graphical explanation of constructed solutions
In this section,we have explained the results of the coupled nonlinear system of the model for ISWs and LWs by drawing some 3D,2D and the contour figures of the succeeded solutions with the support of the symbolic calculation software Maple.The graphical illustrations of 3D,2D and contour plots for some of the obtained solutions are given in figures 1–12.Figure 1 depicts the 3D plot,2D plot and the corresponding contour plot of solution E11(x,t) that behaves like the spike shape solution.Figures 2,11 and 12 depict the 3D plot,2D plot and the corresponding contour plot of solutions n11(x,t),E45(x,t) and n45(x,t),respectively,that represent the singular soliton solutions.Singular solitons are other varieties of solitary waves that give up under a singularity,typically countless discontinuity.Moreover,they can be connected under solitary waves when the midpoint location of the extraordinary wave is missing.Simultaneously,with these lines it is not necessary to address the problem of singular solitons.This answer has spiked and,in this manner,can likely clarify the improvement of rogue waves.Figures 3–6,8 and 10 depict the 3D plot,2D plot and the corresponding contour plots of solutions E13(x,t),n13(x,t)E14(x,t),n14(x,t),n23(x,t) and n24(x,t),respectively,that represent the periodic wave solution.Herein,the special kind of periodic wave solutions of the solutions E23(x,t)and E24(x,t) are shown in figures 7 and 9.
4.Conclusion
In this work,we successfully executed the modified(G′/G)-expansion approach to obtain the closed-form wave structures of the studied equation.Furthermore,this approach concerned new closed-form wave structures like rational,trigonometrical and hyperbolic function solutions.The techniques prescribed the well-designed systems for supervising various nonlinear wave equations with integer-order and also with fraction order arising in several applications of applied sciences.As can be seen from the above solution process,the modified (G′/G)-expansion method is very effective for solving different types of NPDEs.Our results show that the structures of the obtained wave solutions are multifarious in nonlinear dynamic systems.In the near future,we will modify the algorithm presented here to deal with different NPDEs when their coefficients are variables,for exhaling nonautonomous wave solutions.

Figure 1.Graphical descriptions of the solution E11(x,t) under the values p=2,q=0.5,r=2,μ=1,λ=3 and t=0.01 for 2D graphics.
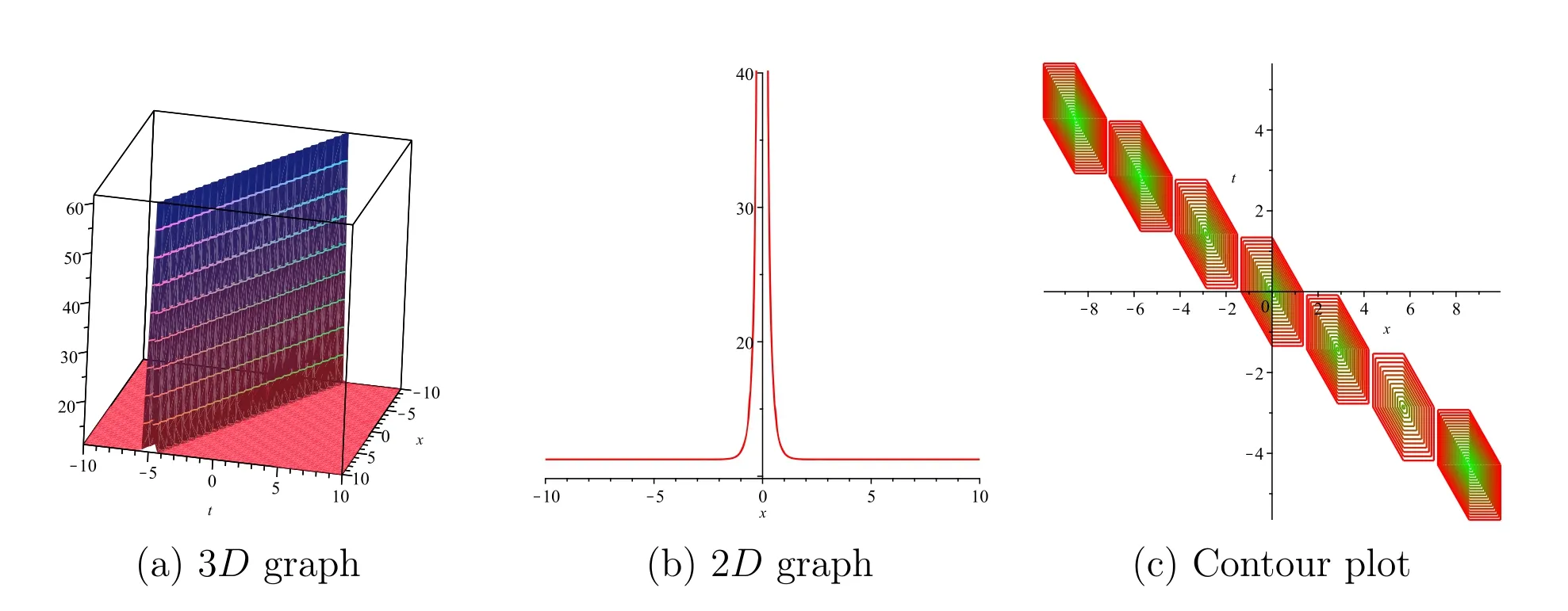
Figure 2.Graphical descriptions of the solution n11(x,t) under the values p=2,q=0.5,r=2,μ=1,λ=3 and t=0.01 for 2D graphics.

Figure 3.Graphical descriptions of the solution E13(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.
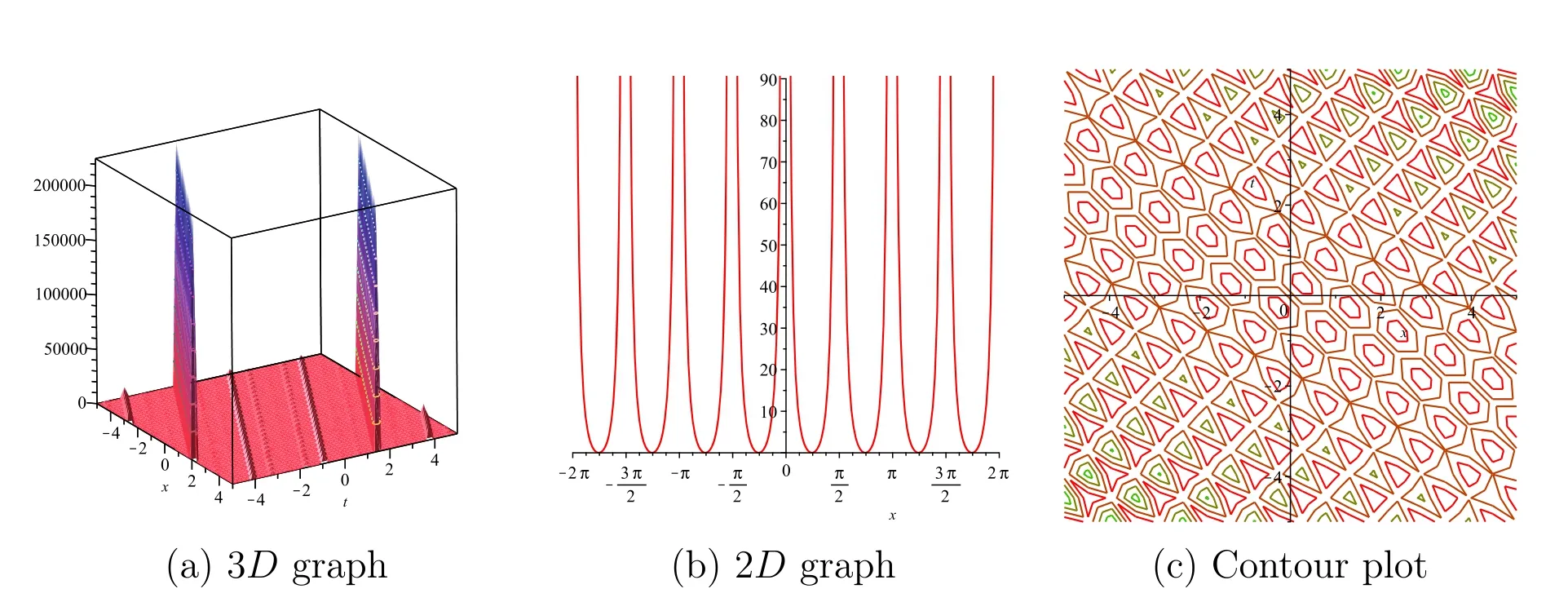
Figure 4.Graphical descriptions of the solution n13(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.
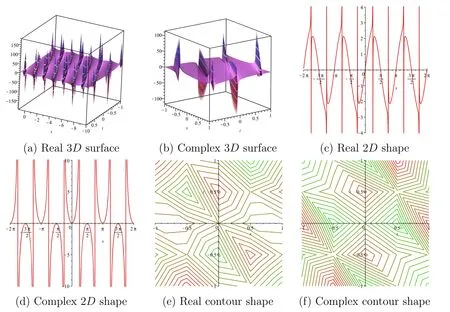
Figure 5.Graphical descriptions of the solution E14(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.

Figure 6.Graphical descriptions of the solution n14(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.
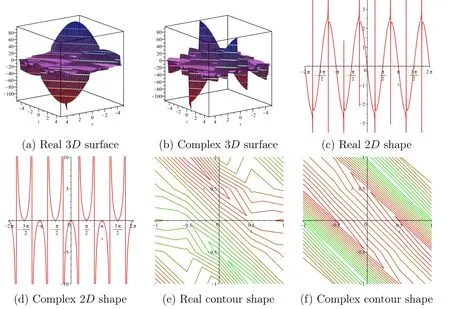
Figure 7.Graphical descriptions of the solution E23(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.

Figure 8.Graphical descriptions of the solution n23(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.

Figure 9.Graphical descriptions of the solution E24(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.

Figure 10.Graphical descriptions of the solution n24(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.

Figure 11.Graphical descriptions of the solution E45(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.

Figure 12.Graphical descriptions of the solution n45(x,t) when p=2,q=0.5,r=2,μ=2,λ=2 and for 2D graphics t=0.01.
ORCID iDs
杂志排行
Communications in Theoretical Physics的其它文章
- First-principles study on superconductive properties of compressive strain-engineered cryogenic superconducting heavy metal lead (Pb)
- Majorana–Kondo interplay in a Majorana wire-quantum dot system with ferromagnetic contacts*
- Effect of Zn doping on electronic structure and optical properties zincblende GaN (A DFT+U insight)
- Exploring the influence of microRNA miR-34 on p53 dynamics: a numerical study*
- A new approach for modelling the damped Helmholtz oscillator: applications to plasma physics and electronic circuits
- Coexistence and fluctuations phenomena with Davidson-like potentials in quadrupole–octupole deformed nuclei
