The dynamical creation/annihilation of a Dp-brane from D(p −2) branes
2021-04-12XiaoyingZhu
Xiaoying Zhu
Department of Modern Physics,University of Science and Technology of China,Hefei,Anhui 230026,China
Abstract
Keywords: D-brane dynamics,noncommutativity,brane generation
1.Introduction
In[1],it was found the dynamical creation and annihilation of a spherical D2 brane from N D0 branes via a background flux which extends earlier work of the static creation of a higher dimensional brane from lower dimensional ones via a background flux [2–5].The natural question is: Is such a dynamical process true only for this particular case or can it be generalized to other p-branes? The other question is: Is the presence of such a background flux necessary for this dynamical process to occur? We try to provide answers to these questions in this paper for a particular class of a Dp-brane from N D(p−2) branes with p≥2.As we will see,the presence of a relevant background flux is not necessary and all we need is the so-called excess energy above the corresponding BPS bound of N D(p−2) branes for such a dynamical process to occur.Some related earlier work can be found,for example,in [6–9].
As we will see,for p≥3,we have the freedom in finding spatial dependent solutions in addition to the time dependent ones.Some of these spatial-dependent solutions and the related ones have been found previously in [10–16].These spatial-like solutions can be viewed as the Euclidean versions of the time-dependent ones.The investigation into the spatial dependent ones can be parallel to that for the timedependent solutions.We find four kinds of the dynamical spherical Dp-branes in the presence of a background flux,depending on their respective excess energy.Each of them has a novel profile along the chosen spatial direction and can also be interpreted as the Dp brane–anti Dp brane system.These solutions will show that when an extended object has an excess energy above the corresponding BPS bound,its size will grow even if no background flux is present,therefore lending support to the spacetime uncertainty principle [17].Other relevant or related works include those in [18].
The paper is organized as follows: we begin in section 2 by providing a short review on the non-abelian action describing N D(p−2) BPS branes and taking proper approximation for the configurations of our interest.Then we present the equation of motion for the transverse non-abelian scalars which is the starting point of our discussion.In section 3,we will consider the simplest but non-trivial timedependent Dp brane from N D(p−2)branes with or without the background flux.In section 4,we will discuss in detail the simplest but non-trivial spatial-dependent solutions and their essential characteristic behaviors,then provide physical explanations to them.In section 5,we have a glance at the space–time dependent Dp branes by applying the Lorentz boost σa(witha= 0,1,…,(p−2)) to the Dp branes discussed in the previous two sections.Section 6 ends with a discussion of the implications of the present work.
2.The set up
For the purpose of finding a dynamical spherical Dp-brane from N BPS D(p−2)-branes p≥2 via an RR(p+2)-form(or even with no such a background flux),we need to have a proper action in describing the N D(p−2)BPS branes and also a DBI action which describes a single Dp-brane with the same background but with a worldvolume magnetic flux.The latter is easy to obtain but the former needs some effort for which we are making now.This set up was also mentioned in[19]and discussed partially in[3].We know that the low energy effective action of N D(p−2)branes is a U(N)non-abelian generalization of the corresponding DBI action for a single D(p−2)-brane.The general precise form of such a non-abelian action is still unknown but Myers proposed[2,20] a form based on T-dualities which is believed to be correct at least to the orderO (λ2)with λ=2πα′.We take such a limited non-abelian action describing N D(p −2)-branes as our starting point and we try to take a proper account such that this kind of action is enough for our purpose.We consider a flat background with a constant RR (p+2)-form flux as
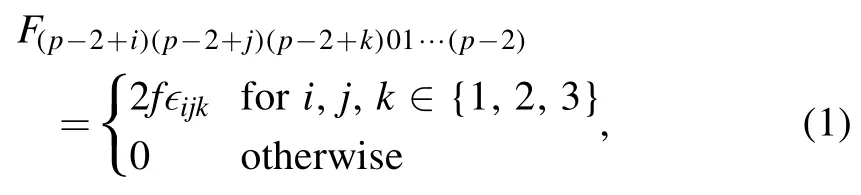
with f carrying dimensions of length−1.We also take bulkBμν=0.As we will discuss in the following,for the confgiurations of our interest and the approximations taken,we can set zero the worldvolume gauge field consistently.As in [20],we take static gaugeσa=xafora= 0,1,…,(p−2).With the above background,we have the bosonic part of the DBI action including the worldvolume gauge field to the order of λ2as
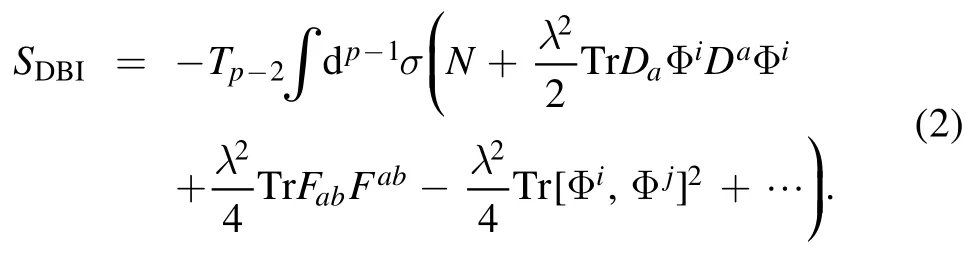
We try to find the conditions for which we can set the worldvolume gauge field to zero consistently.From the above action,the equation of motion for the gauge field is
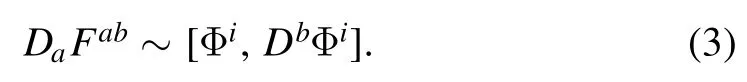
If we set Aa=0,then we must have a consistent condition

Only when this condition is satisfeid,we can set the worldvolume gauge feild to zero consistently.Given this,we also need to keep in mind that we need to fnid conditions under which the above DBI action to order ofO (λ2) is a good one.As we will see,all these can indeed be met for the time-dependent confgiurations considered in this paper.For spatial-dependent ones,there exist two dual descriptions of the same dynamics which are valid in complementary regions of parameter space [20].Just like the time-dependent cases,these two descriptions agree when the number of lower dimensional coincident D-branes are large.Therefore,we need to consider only the following DBI action
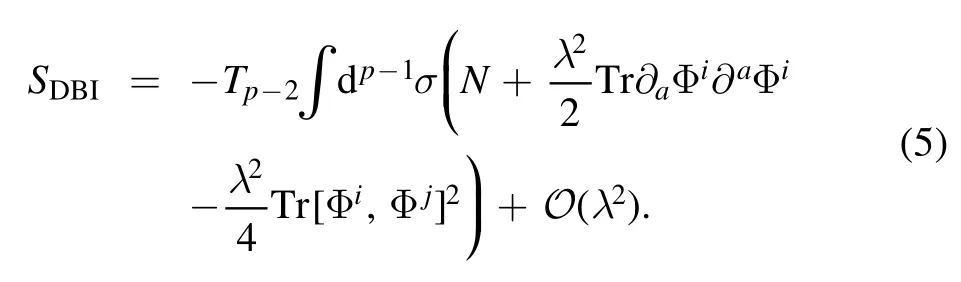
Given the above background,the exact Chern–Simons action is,following [2]
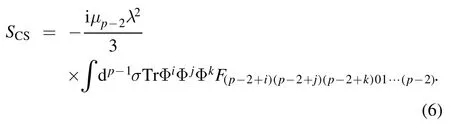
Therefore the total low energy effective action of N D(p−2)branes up to order ofO (λ2) is
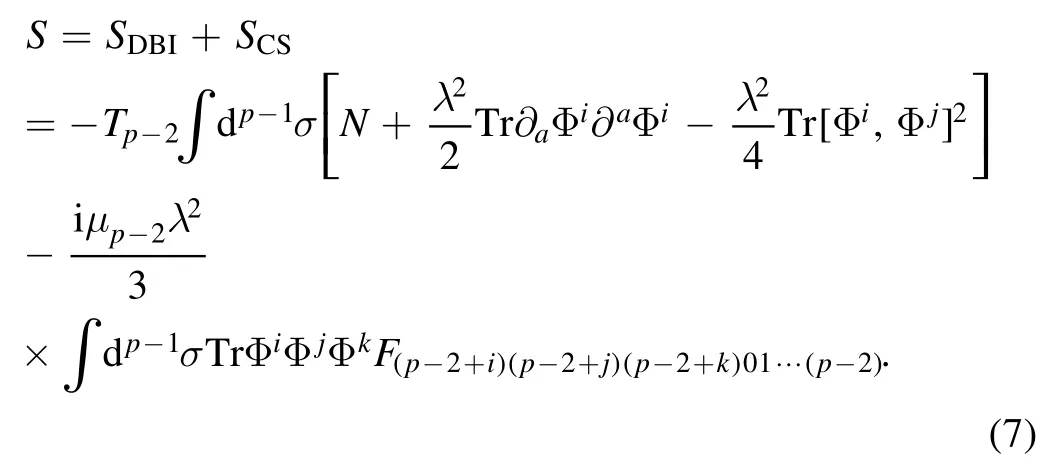
We have Tp=μpwith
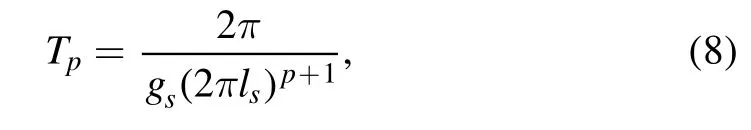
where gsis the string coupling and lsthe string length scale.The corresponding Hamiltonian density from the above is

The corresponding potential density is

The equation of motion from the above action (7) is
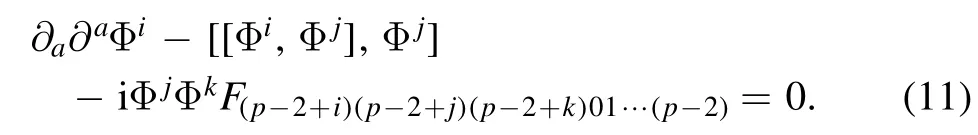
Let us now plug the expression for the RR (p+2)-form flux given in (1) to the above and we have
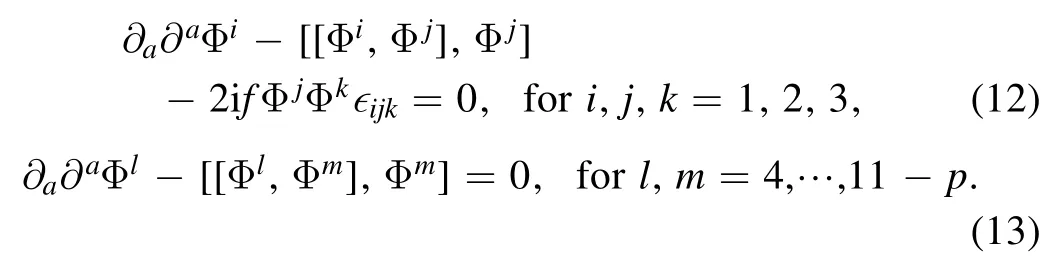
In the above,one should not confuse the imaginary number i with the spatial index i.
In obtaining the above,we have assumed [Φi,Φl]=0 which is true for the consideration of this paper.Once this is assumed,the Φiand Φlare decoupled and we can consider them separately.The above two equations serve the starting point of our discussion in this paper.
3.The simplest non-trivial time-dependent Dp brane
We focus in this section on the simplest but non-trivial timedependent Dp brane from N D(p−2)branes.This is a direct extension of the cases considered in [1,7].Let us consider(13)first.As discussed in[7],the non-trivial solution must be in a non-trivial representation of certain group and must be time-dependent1We here consider either time-dependent or time-independent configuration.The spatial-dependent ones are postponed to the following section..For example,if we take three of Φlin a N×N representation of a SU(2),i.e.φ3+i=g(t)Kiwith the SU(2) generators Ki(i=1,2,3) in this representation and the rest are trivial,then equation is simply reduced to

which can be integrated once to give

with obviouslyW=E2≥0(we assume E≥0 without loss of generality).At fixed t,the above ansatz for the non-abelian scalars describes a non-commutative two-sphere with a physical radius given by
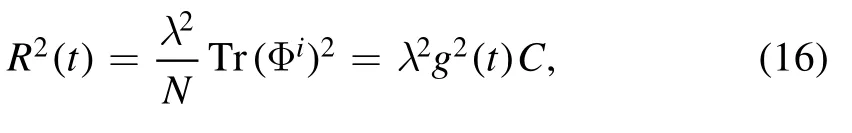
where the repeated indices represent summation and C denotes the quadratic Casimir of the particular representation of the generators under consideration,defined as

with1N×Nthe unit N×N matrix.For example,C=N2−1 for the N×N irreducible representation.For convenience and simplicity,we will take the N×N representation as the irreducible one from now on unless stated otherwise.This equation has a periodic solution of time as
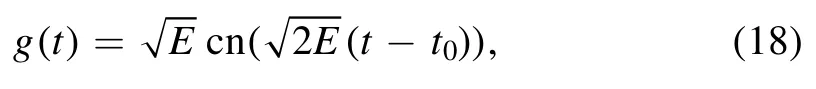
where E2is proportional to the contribution of excess energy from these directions.cn(x) is a Jacobian elliptic function,which,likecosx,is a periodic function with its value taking between −1 and 1 and whose real period is 4K with K the complete elliptic integral
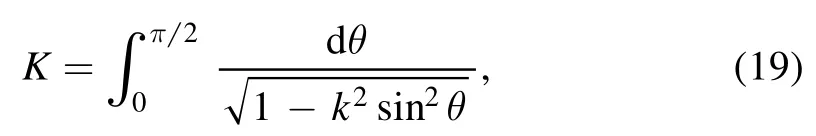
where k2=1/2 with k the modulus.This solution indicates that we can create a dynamical Dp brane with topologyfrom N D(p−2)branes onceE>0 even without the presence of any background flux,again lending support to the spacetime uncertainty principle proposed in [17] and the space noncommutativity [21–27].This time-dependent configuration can also be found from a single Dp brane with a topology ofand with a worldvolume U(1)magnetic flux as discussed in [2] (similar discussion with a non-vanishing background flux will be briefly presented at the end of this section).This consideration also sets the limits for the parameter E which validate the approximation made in the previous section.We actually need E ≪2/(λN).Even with this,the physical radius of the fuzzy sphere can still be large for large N in units of string length lssince from(16)and for large N,

In the remaining part of this section,we consider φifrom equation (12).The non-trivial solution can be obtained by taking Φiin the N×N irreducible representation of another SU(2),i.e.φi=u(t)Jiwith the SU(2) generators Ji(i= 1,2,3) in the N×N irreducible representation.Then equation (12) is reduced to

This is exactly the same as the one given in [1] for finding a dynamical spherical D2 brane from N D0 branes via a constant RR four-form flux,therefore we expect the same three kinds of solutions found there.The various properties and the critical behavior of the solutions and how these depend on the excess energy have been discussed in detail in[1]and also in[7],we will present the solutions briefly below and the discussion of their properties are referred to [1].The only difference between the present case and the one in[1]is that for p≥3,the dynamical Dp brane has a topology ofRp−2×S2rather than merely a p-dimensional sphere.The above equation can be integrated once to give

with W the integration constant proportional to the excess energy.To have a clear physical picture of the following,we define the so-called reduced potential for the system under consideration as

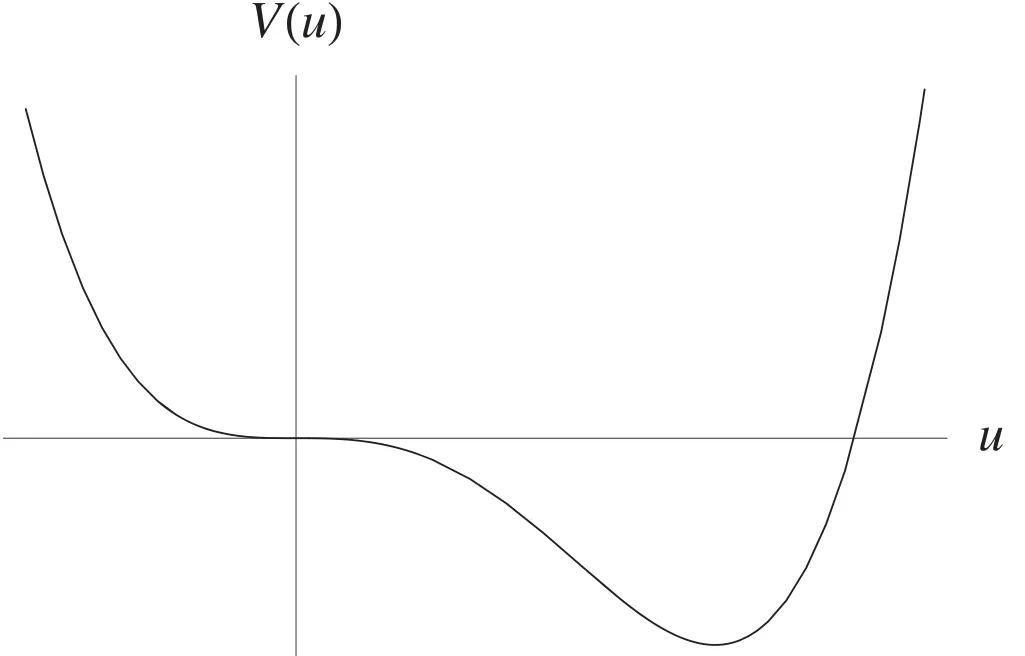
Figure 1.Plot of the reduced potential V(u).
withV the potential density given in (10).The profile of the reduced potential is shown in figure 1.The integration constant W is now twice the corresponding reduced excess energy defined aswith H the Hamiltonian density given in (9).
For the purpose of finding the solution to(22),we define the polynomial

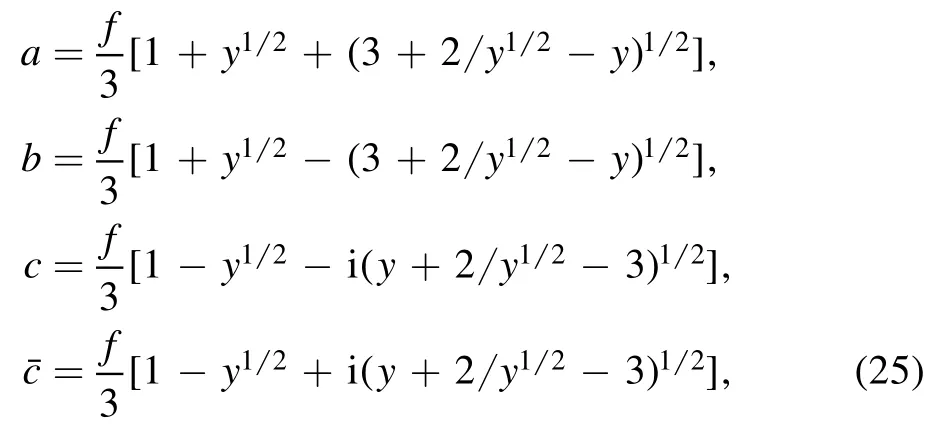
where

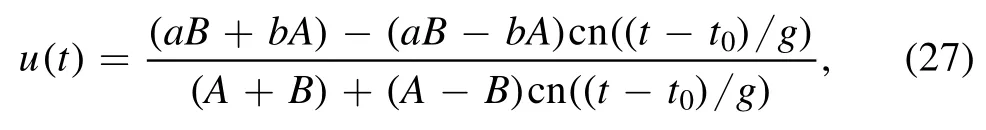
where A,B,g,k are given as
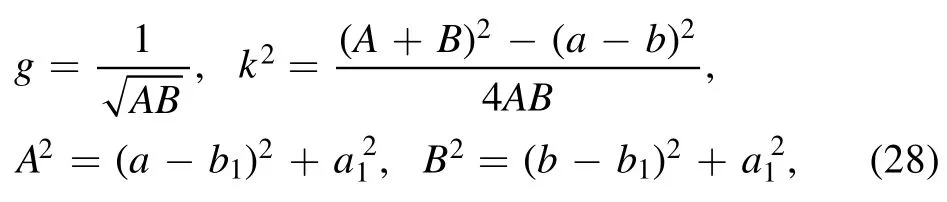
with
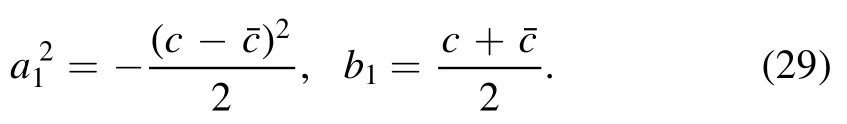
The real period 4K of cn can again be found once we have the complete elliptic integral (19) for K with the present k2given above.
For W=0,the solution can be expressed in terms of a simple function as

The time-dependent behavior of this solution can be similarly discussed as in [1] for p=2.It represents a dynamical creation and annihilation of a Dp brane with a topology offrom N D(p−2) branes with a topology of Rp−2.
For W>E2>0,the time-dependent configuration can continuously be given by equations (26)–(28) witha,b,c,given by (24) but now we have a different y given as
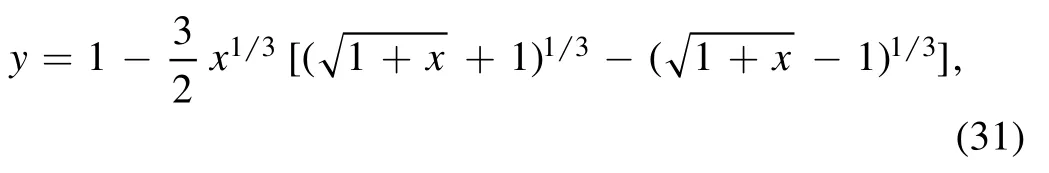
The present Dp solution can also be found from a single Dp brane action with a p-dimensional worldvolume U(1)fluxrepresenting N D(p−2) branes,for example,see [1,2],and the following metric

In doing so,we take static gaugeand take the radial coordinate R to be time dependent and xlto be constant.As in [1,2],we further need to take the motion to be non-relativistic,i.e.andwhich can indeed be satisfied consistently for the solutions found.Notice also that− 2fR2sinθ→Ctθφ12…(p−2)=(2fR3sinθ) 3.With all these,the equation of motion for R(t)can indeed be reduced to(21)for u(t) above if we identifySoimplies thatwhich also impliesAgain the above discussion with an RR(p+2)flux can be generalized to different fuzzy cosets as discussed in [3].For time-dependent soluions,we can also consider having some RR flux along certain fuzzy directions and certain fuzzy directions with no flux,i.e.combining the two previous discussions,one along i,j directions and the other along l,m directions.
4.The spatial-dependent Dp brane
In addition to the time-dependent solutions discussed above,the other simplest but non-trivial solutions are those dependent on a single spatial coordinate.Without losing generality,we can take,for example,this spatial coordinate as x1=σ1=σ.The present discussion can be parallel to what we did in the previous section for time-dependent solutions.The p=3 case with no background flux,by the name of funnel solution,has been discussed in[20]and is taken as the‘dual’ to the spike-like bion solutions in the abelian worldvolume theory of a single D3 brane which were discussed previously in [10,11].The same system has also been analyzed previously in[13–15].The extension to a general p with no background flux was also mentioned in[19].Even for this case,our interpretation is however slightly different from that given in[19].We also discuss the case with the presence of a constant RR (p+2)-form flux.
Let us consider first the solution along 4,…,11−p directions forp≥ 3 and focus on the case when no background flux is present.For this,we can take three of the Φl's,for example,in the N×N irreducible representation of a SU(2),i.e. φ3+i=g(σ)Ki(i=1,2,3) with the SU(2)generators Kiin this representation,and the rest are trivial.Then from (13) we have


with W the integration constant.Here W can be either negative,zero or positive.
ForW= −E2≤0,it is not difficult to see from the effective potential~−g4in(34)that we have two branches of solutions,one withwhile the otherThe corresponding solution to the above equation can be solved in terms of Jacobian elliptic functions sn and cn as
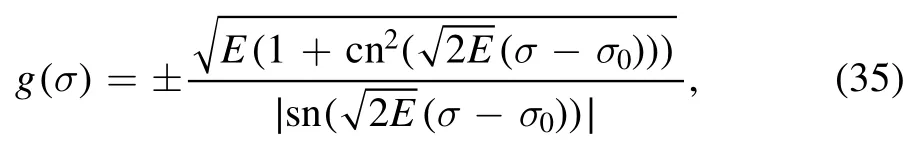
where the plus sign gives the solution ofwhile the minus sign givesWe have the real period 4K of the Jacobian elliptic functions sn and cn with K the complete elliptic integral given by (19) with now k2=1/2.We choose the plus sign above for the following discussion.Given that both sn and cn fall between −1 and 1 and their real period 4K,we havewith a period of 2K.Whenσ=g(σ) = ∞whileσ=σ0+Here n is an integer.Whenever→∞,i.e.the opening up of three more infinite dimensions in this limit and therefore having a D-brane with its spatial dimensionality ofp− 2 − 1 + 3 =p.In other words,we have an infinitely extended Dp brane located at everyσ=with n an integer.The identification of this can be along the same line as given in[19].Note that near each of these points along the σ-direction,the newly opened dimensions look like a funnel while the rest (p−3) dimensions remain the same as before.Each of these funnels contracts first,then reaches a minimum radius whenσ−σ0=then reexpands into another brane.This process repeats itself along the σ-direction.Note that the corresponding physical radius isTherefore,we have an infiniterepetition of the funnels or wormholes along the σdirection in dual Dp-brane framework [10,11,19].Here our interpretation of the solution differs slightly from that given in[20].For p=3,they took the ‘dual’ viewpoint to the spikelike bion solutions in the abelian world-volume theory of the Dp brane given in [10,11].For the spike-like bions,it is perfectly fine to take σ as a function of radius r on the Dp brane with 0<r<∞(using our notation here).For the present case,the variable is σ with −∞<σ<∞and the radius r or equivalent g(σ)is a function of σ and the range of its value is determined by that of σ rather than the other way around as did in [19].For this reason,the periodic profile is similar to that given in figure 2 for the case of W=E2>0 discussed later along the σ-direction rather than just the funnel as given in [19].The conventions on brane and antibrane from [10] are as follows: ifg′ >0 at the location of brane,we would call it brane otherwise we call it anti-brane.With this,the interpretation for the branes are also similar to the case of W=E2>0 and we refer there for detail.

Figure 2.The profile g (σ) for the case of W=E2>0.The characteristic behavior of the case W = − E2 <0is similar but with the following differences:and at g(σ )=
For E=0,we can solve either directly from(34)or take the limit E →0 from aboveW= −E2<0solution to have
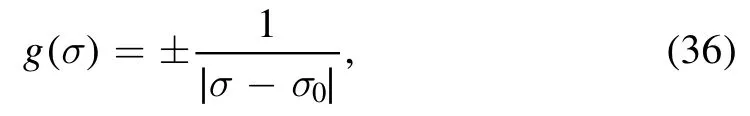
which is actually a BPS configuration and solves even the complete DBI action in either complimentary description as discussed in [10,11,19].The interpretation of these two solutions can be similarly discussed following [10].
If the integration constant W=E2≥0,the solution to(34) is now

Here eitherg(σ)≥0org(σ)≤0.As E →0,we have

as expected.Unlike the previous case ofW= −E2discussed,the present profile is now periodic with a real period of 4K(see figure 2).Here the complete elliptic integral K is given by(19) with k2=1/2.For simplicity,we take σ0=0 in the figure.We need to consider only the range of<4Kand the rest would be clear from this.For plus sign in(37),the brane located at σ=0 represents an anti Dp brane with respect to the wormhole at its right side since nowg′(0+)<0 while it appears as a Dp brane to the wormhole at its left side since nowg′ (0−)>0 .To the right side of this brane,the funnel collapses to zero size,then reexpands into an Dp brane atσ=To the left,the funnel collapses to zero size and then re-expands into an anti Dp brane atSo a brane will appear atwith n an interger.For present case,whether it is a Dp brane or an anti Dp brane depends on which side one is referring to.A brane is always a Dp-brane when the wormhole appears at its left side and an anti Dp-brane when the wormhole appears at its right.If we choose the minus sign in (37) instead,the above brane and anti-brane are just reversed.
The above discussion can be applied either to equation(13)alongl,m= 4,…,11 −pdirections or the case for the system under consideration without the presence of a background flux.From now on in this section,we focus on(12).Since the i=1,2,3 directions are decoupled with thel,m= 4,…11 −pdirections as mentioned before,we can discuss these two parts independently.We now assume that each Φiis in the N×N irreducible representation of another SU(2) by φi=u(σ)Jiwith SU(2) generators Jiin the same representation2We could assume that Ji in a general,either reducible or irreducible,representation of SU(2)since all we need at the end is the quadratic Casimir..Then we have from (12)

Integrating this equation once,we have

with W the integration constant.To facilitate finding solutions to the above equation,we introduce the so-called analogous particle whose kinetic energy is given bymoving in a potential−V(u) with V(u) the reduced potential (23)
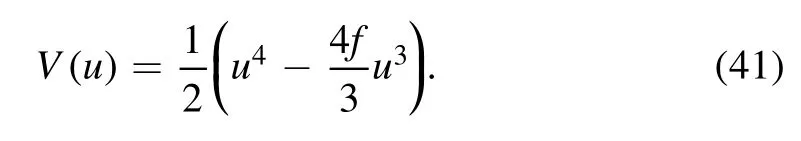
Then the constant W is twice the total energy of this analogous particle.Note that the actual total energy is proportionalWith the analogous particle,we can have a better picture in finding solutions.The extremes of the potential−V(u)are at u=0,f respectively.But−V″ =0 at u=0 while−V″ = − 2f2<0at u=f ,therefore u=0 is merely a turning point while u=f gives the maximum of−V(u).Also−V(u= 0) =0and −V(u=f) =Given this information,we can now discuss the solutions.For the purpose of solving the above,we need to define the following polynomial

Case 1:W>f4/3,now the polynomial P(u)has no real roots.The essential characteristic behavior of the solution has not much difference from the W>0 case when f=0 discussed above and we will not repeat the solution here.
Case 2:0<W<f4/3,the polynomial P(u) has two real roots a,b with a>b>0 and two complex ones c andwhich are complex conjugate to each other.They are

where


where

with
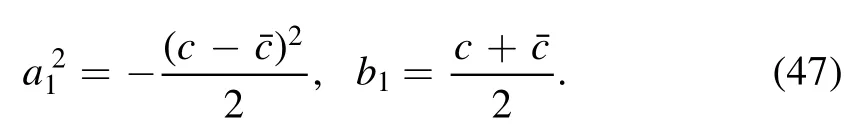
One can check indeed either u(σ)>a or u(σ)<b.Thinking in terms of the motion for an analogous particle,we don’t have difficulty in understanding the above.The potential−V(u)has a barrier of hight f4/6 and now the particle has an energy in the range 0 <W2 <f4/6which is positive but is lower than the barrier.When the motion of the particle is either on the left or the right of the potential barrier,classically it will keep its motion either in the u(σ)>a region or in the u(x)<b region since its velocity will be zero when it reaches u (σ)=b from left or u (σ)=a from right.It does not have enough energy in moving beyond that point classically.Note that here b>0,so the radius of the two-sphere moving on the left side of the barrier can be zero.The real roots a>b>0 can indeed be checked by noticing when 0<x<1,the value of y falls in-between 1 and 4 from (44)and (43).Therefore,classically,the two-sphere radius for the motion on the right side of the potential barrier can not be zero (since u (σ)>a) while for the motion on the left,the corresponding radius can be zero since u(σ)<b with b>0.

Figure 3.The profile of 0<W<f4/3.
Let us discuss in some detail the profile of u(σ).For simplicity,we take σ0=0.To have a clear picture of the profile,we need to consider the region of −4K≤σ/g≤4Kwith K the complete elliptic integral for the present case.As σ=0,cn(σ/g)=1 and u (σ)=a.Therefore we expect that u(σ)>a for∣σ∣>0until we reach cn(σ/g ) =(A − B )/ (A+B) at some pointσ= ±σ1where u(σ)blows up.Just passing∣σ∣>σ1in both directions,u(σ)is negative and it reaches the first zeros in both directions when3If b<0,we cannot have this equation satisfied.This will happen in the following Case 4.cn(σ/g= (bA−aB )/(bA+aB)at some pointσ= ±σ2withσ2>σ1.That σ2>σ1can be understood from (bA−aB)/ (b A +aB ) <(A −B)/(A+B).Then u (σ) will become positive in both directions and reaches its local maximum atσ/g= ±2Kwhere cn (2K) = −1and u (σ)=b.Further,u(σ) will decrease and reaches its second zeros when cn(σ/g= (bA−aB)/(bA+aB).Thenu(σ)will become negative again and blows up when cn(σ/g=(A−B)/(A+B) atσ= ±σ3withσ1<σ2<σ3<4Kg.Passing both of these two points,u(σ)will become positive again and reaches its value a atσ/g= ±4K.After this,the profile will repeat itself according to our above discussion.According to the criterion in identifying a brane or anti-brane given in [10] and mentioned a while ago,for the branch u (σ)≥a,we can determine the brane located at σ=σ1as Dp brane while the one located at σ=−σ1is an anti-Dp brane.For the same reason,the brane located at σ=σ3is an anti-Dp brane while the one located at σ=−σ3is a Dp brane.The brane and anti-brane will be alternating along the σ-axis.For u(σ)≤b,we just reverse the above.We have two kinds of wormholes,one with nonvanishing radius while the other with its radius vanishing twice as shown in the figure 3,and they also appear alternative along the σ-axis.
Case 3:W=0.As happens always,this corresponds to a critical point where the solution can be solved in terms of an elementary function as
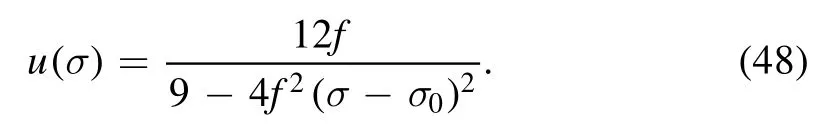

Figure 4.The profile of W=0 case.
This solution is the Euclidean version of the time-dependent one given in [1] by sending (t−t0) →− i (σ−σ0) there.Unlike the corresponding solution in the case of no background flux,u(σ) →4f/3asσ→σ0while u(σ) diverges whenσ−σ0→±3/2f.It approaches zero whenσ→±∞.Therefore we have three more dimensions opening up atσ=σ0±3/2f,respectively.Sinceu′(σ)>0for σ>σ0whileu′(σ)<0for σ<σ0,therefore we expect an anti–Dp brane located atσ=σ0−3/2fwhile a Dp brane located atσ=σ0+3/2f.On the left side of the anti-Dp brane,we have a funnel with its mouth open at the location of the anti brane while the other funnel on the right side of the Dp brane with its mouth open at the location of brane.There is a wormhole throat which connects the brane and the anti-brane.The wormhole has its minimum radiuswith the quadratic CasimirC=N2−1.The proflie of the confgiuration is given in figure 4.
Case 4:W<0.The polynomial P(u)in(42)has still two real roots a and b with a>b and two complex roots c and,complex conjugate to each other.They are still given by the expressions in (43) but now with y as
wherex= −3W/f4.Since x>0,therefore 0<y<1,giving a>0,b<0 anda>∣b∣which can be checked from(43).The corresponding solution is still given by (45)–(47)and we continue to have either u(σ)>a or u(σ)<b.The important difference between the present solution and the one for 0<W<f4/3 is that we haveb< 0 here,therefore the radius cannot be zero classically on either side of the potential barrier.The present case(here a>0 and b<0 buta≠−b)looks more like the W<0 case of no background flux discussed earlier for which a=−b.The identification of brane and anti-brane is the same as what we did there.We have two kinds of wormholes adjacent to each other in the periodic profile with their minimum radii determined by a and∣b∣,respectively.We will not repeat the analysis here.
5.The space–time dependent Dp brane
In this section,we apply the Lorentz boost along σa(witha=0,1,…(p−2)) to the Dp branes discussed in the previous two sections.By this,we can obtain space–time dependent Dp branes.For the Dp-branes found in section 3,the boosted ones should be time-like while the boosted ones from the Dp branes discussed in section 4 should be spacelike brane.Such obtained Dp branes are still special kinds.There exist great possibilities that more general spacetime dependent brane configurations exist but in this paper we limit ourselves to the above Lorentz boosted ones only.
For each of the time-dependent solutions discussed in section 3,the correspoonding Lorentz boosted one can be obtained simply by replacing the time t by (t−v·σ)/wherev is the boosted (p−2)-dimensional vectorlike parameter andv=∣v∣with v in the range0≤v<1.For example,v= 0,we reproduce the solutions given in section 3.However,in general,the solution depends not only on time but also on the (p− 2)-dimensional coordinates σawitha= 1,…,(p−2).
For each of the σ-dependent solutions discussed in section 4,we can only do limited Lorentz boost,i.e.we can only boost along the σ-direction,i.e.replacing the σ byAgain,v=0 gives back the original one.
6.Discussions
By making use of the non-abelian action describing N D(p−2) BPS branes,in section 3,we show that the time evolution of the dynamical Dp-brane for a general p remains the same as for the p=2 case[1].We also provide evidence in support of the spacetime uncertainty principle by finding that we can create a dynamical Dp brane with topologyRp−2×S2from N D(p−2) branes once there is excess energy above the corresponding BPS bound even without the presence of any background flux.
In section 4,we can see that the spatial-dependent solutions with or without the background flux can also be interpreted as the Dp brane-anti Dp brane system since the D(p−2) branes expand out in a funnel-like geometry to become orthogonal Dp branes as well as anti Dp branes.Note that our analysis has been limited to large N world-volume theory in each case.These solutions can also be found in the dual abelian Dp brane action description.The equation of motion for R(σ)can be reduce to the u(σ)ones in section 4 if we identifyWe need to takeimplying thatu2≪ 2 /(λN).This in turn saysIn particular,for large N,both u(σ) and f are tiny but the radius of the Dp brane can still be large.The smallness of u(σ) makes our ignoring higher order terms in the matrix action justified while that of f implies that the flat background satisfies the bulk equations of motion to the leading order since now the metric correction due to the presence of the four-formδ hμν≪1 as discussed in [5].
Acknowledgments
The author would like to thank J X Lu for fruitful discussion and acknowledge support by a grant from the NNSF of China with Grant No: 11 775 212.
杂志排行
Communications in Theoretical Physics的其它文章
- First-principles study on superconductive properties of compressive strain-engineered cryogenic superconducting heavy metal lead (Pb)
- Majorana–Kondo interplay in a Majorana wire-quantum dot system with ferromagnetic contacts*
- Effect of Zn doping on electronic structure and optical properties zincblende GaN (A DFT+U insight)
- Exploring the influence of microRNA miR-34 on p53 dynamics: a numerical study*
- A new approach for modelling the damped Helmholtz oscillator: applications to plasma physics and electronic circuits
- Coexistence and fluctuations phenomena with Davidson-like potentials in quadrupole–octupole deformed nuclei
