Investigation of quark distributions in a family of pentaquarks using the Thomas–Fermi quark model
2021-04-12MohanGiriSumanBaralGopiChandraKaphleNirmalDangiSudipShiwakotiLeonardoBardomeroPaulLashombandWalterWilcox
Mohan Giri,Suman Baral,Gopi Chandra Kaphle,Nirmal Dangi,Sudip Shiwakoti,,Leonardo Bardomero,Paul Lashomb and Walter Wilcox,,∗
1 Department of Physics,Baylor University,Waco,TX 76798,United States of America
2 Everest Institute of Science and Technology,Kathmandu,NP 44618,Nepal
3 Central Department of Physics,Tribhuvan University,Kirtipur,NP 44600,Nepal
4 Neural Innovations LLC,Lorena,TX 76655,United States of America
5 Division of Health Science and Mathematics,Niagara County Community College,Sanborn,NY 14132,United States of America
Abstract Using the Thomas–Fermi quark model,a collective,spherically symmetric density of states is created to represent a gas of interacting fermions with various degeneracies at zero temperature.Over a family of pentaquarks,uudc,color interaction probabilities were obtained after averaging over all the possible configurations.Three different functions are developed for light,charm,and anti-charm quarks and are assumed to be linearly related by some proportionality constants.Interesting patterns of quark distributions are observed while analyzing the quark function consistency conditions for such constants.
Keywords: quark models,Thomas Fermi models,pentaquarks
1.Introduction
Over the last two decades the existence of multi-quark states such as pentaquarks and tetraquarks have been confirmed through the efforts of the LHCb [1–4],BESIII [5,6],Belle[7–10]and other collaborations.One can expect even more to be discovered in the years to come.The measurements of the state productions by the LHCb [4] were determined to be pentaquark states of quark flavor contentuudc.Specifically,the measured charmonium-pentaquarks were the PC(4312)+,PC(4440)+,and PC(4457)+.
One of the standard theoretical methods to investigate such multi-quark states is lattice quantum chromodynamics(LQCD).As the quark content increases,however,LQCD becomes more computationally expensive and time-intensive.A great deal of effort on theoretical setup in terms of Wick contractions,operator selection,wave function smearing and analysis must be done.Each state must be investigated separately and no global picture emerges.Larger systems also require larger lattices.In order to investigate the dynamics of such exotic states,the Thomas–Fermi (TF) statistical quark model was developed[11] as an inexpensive alternative.We have pointed out that it could be key to identifying families of bound states,rather than individual cases[12].The TF quark model has previously been applied to systems of multi-quarks to investigate ground state properties of baryons[13,14].It has also been used to examine the bound states of multi-quark mesons [15].The latter paper suggested the existence of several tetra,octa,and hexadeca quark states.Due to its timely experimental significance,in this paper we begin a theoretical investigation of the quarkdistributions for the family of multi-charmonium pentaquarks.These would include penta (5),deca (10),pentedeca (15),…collections of quarks and antiquarks,where we require one additionalcombination per penta addition.

Table 1.Five different ways to obtain a color singlet.
The paper is organized as follows.We first develop a formalism to count the number of color interactions in section 2.In section 3 we put flavor and color interactions together,convert a discrete system of particles into a continuous system,and obtain normalization conditions.After that,we introduce the TF statistical quark model and obtain expressions for potential and kinetic energies in sections 4.The energy is minimized by varying the density of states and TF differential equations are obtained in section 5.The consistency conditions are then formulated in section 6 for various quark contents and degeneracies.We examine the resulting radial distributions of three different types of quarks (light,charmed and anticharmed)in section 7.Finally,we give conclusions and outline of further work in sections 8 and 9.
2.Residual color coulombic interactions
The types of possible color interactions will be six in number,the same as in [15]; namely,color–color repulsion (CCR),color–color attraction(CCA),color-anti-color repulsion(CAR),color–anti-color attraction (CAA),anti-color–anti-color repulsion(AAR),and finally anti-color–anti-color attraction(AAA).The statistics,however,will differ from before.In this section,we will determine the average number of times a given interaction will occur,perform a cross check on the calculations,and finally see that the system is bound through residual color coupling alone even in the absence of volume pressure.
2.1.Occurrence of color interactions
Due to color confinement,objects made from quarks must be SU(3) color singlet states in order to exist as free particles.Color singlets can be achieved in five different ways,as shown in table 1.
A pentaquark is a system of either four quarks and an antiquark or four anti-quarks and a quark.In order for it to be a color singlet,other arrangements are not possible.This requirement for pentaquarks to be color singlets,and the various ways they can form color singlets affects the number of occurrences of color interactions.For example,a system of ten particles could equally be two red,two blue,four green and two anti-green;or two red,three blue,three green,one anti-blue and one anti-green.So,when we talk about the occurrence of colorinteractions,there is some probability for each occurrence.We calculate such probabilities for a system of 5η particles in this subsection.For convenience,we refer to a color singlet consisting of five quarks as a pocket.This means a system of 5η particles have η pockets in total.Any pocket could equally be one of the six possibilities as shown in the table 2 below.

Table 2.Different ways a color singlet pocket could be formed.

Table 3.Possible quark interactions between the same type of pocket.
In this paper,we are investigating structures of a family of hidden charm multi-pentaquarks.So,our system of fermions can have only the first three pockets from the table.We will let x be the number ofpockets,y be the number ofpockets,and z be the number ofpockets so that

Since all particles in this system of 5η particles can interact with each other through color,there will be a total ofinteractions.At the same time,we cannot be sure how the singlet is achieved in each pocket; we can only tell they are one of the three possibilities.This gives rise to 3ηpossible configurations and,at any given time,the system would be found in one of those configurations.In order to give equal footing to all the color combinations,we counted all the possible interactions across all configurations.In this distribution,there will beoccurrences across the six possible color interactions.In order to simplify the calculation,we distribute the calculation into three different categories and put them together in the sub-subsections to follow.
2.1.1.Occurrence of interactions between same type of pockets.Here,we count the number of occurrences for interactions between the same type of pockets.For example,when apocket interacts with anotherpocket,as given in table 3,we can have six CCR type of interactions,ten CCA type of interactions,and so on,as shown in table 4.

Table 4.Occurrence of interactions between the same types of pockets.

Table 5.Possible quark interactions between two different types of pocket.

Table 6.Occurrence of interactions for different types of pocket.
2.1.2.Occurrence of interactions between different pockets.Here,we count the number of occurrences of interactions between different types of pockets.For example,when anpocket interacts with apocket,as given in table 5,we can have five CCR type interactions,eleven CCA type interactions,and so on.The complete list is shown in table 6.

Table 7.Interaction within the same pocket.
2.1.3.Occurrence of interactions within each pocket.The last case we need to consider are interactions within each pocket.We will first consider the pocketIf we first consider r,it can interact with all of the other four quarks,namely,rr,rb and rg.If we then consider the interactions involvingthere are four possibilities,but only three unique interactions that we have not yet counted,namely,,andSimilarly,the two unique interactions involving the second r that have not been previously counted are rb and rg.Lastly,b interacting with g as bg is the only remaining unique interaction and we have now counted all of the interactions.The results are shown in table 7 below.
Exactly the same number of possibilities can be constructed foras well as for.Therefore,the total number of times CCR type of interaction can occur is η,CCA is 5η and so on.Here,we have used the fact that x+y+z=η.
2.1.4.Calculation of total number of occurrences.In the next step we varied x from 0 to η and y from 0 to(η−x) ,thereby giving equal footing to all the color combinations and counted color interactions.Eigives the total number of occurrences of the ith color interaction out of 3η5η(5η −1)/2.Putting together what we obtained in previous sections,we have for Ei:

Here,Eihas been expressed in terms of vectors where the components of each of the column vectors denote the calculations summarized in tables 4,6,and 7.The first term in Eicorresponds to the interactions within a pocket,the second term corresponds to interactions between the same type of pockets,and the last corresponds to interactions between different pockets.As an example,the first component of Eitells us the total number of occurrences of the ith color interaction involving CCR which can are made up by CCR interactions within a pocket,between the same type of pockets,and between different pockets.
Employing Mathematica,equation (2) simplifies to

Since Eiis the total number of occurrences of the ith color interaction,the probability of the ith interaction can be obtained by dividing equation (3) by the total number of possible interactions between the color combinations we’re interested in,3η5η(5η −1)/2.In addition,we define a probability notation that will help us in the calculation of energies.In this new table,i and j refer to colors,P refers to probability of interaction with no anti particle,refers to interaction between one particle and one anti-particle,whereasrefers to interaction between two anti-particles.We also divide by three to provide equal footing for each color.In this notation,we arrive at table 8.
In table 8 it is understood that i <j inand
2.2.Cross check on our counting
As a cross check on the probabilities,adding them up yields
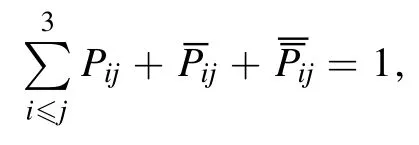
so the probabilities sum to one,as desired.
We will also check our pentaquark model to ensure that it is indeed a color singlet.Let→denote the total color charge of the quarks.By definition,we have,

Squaring both the sides
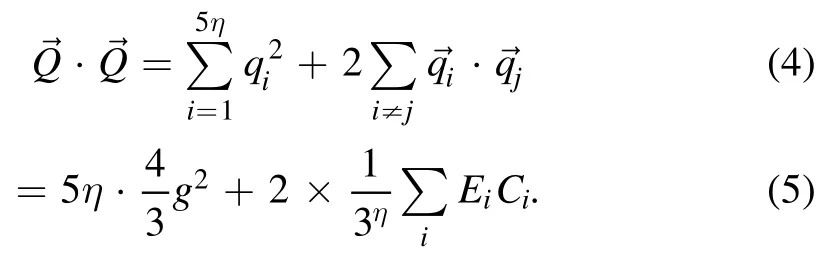

Therefore,using this value

Hence,we see that our model is,indeed,a color singlet.
It should also be noted that,if we add the product of coupling and probability,we find thatHere,the negative sign indicates that the system is attractive because of the collective residual color coupling alone,even in absence of volume pressure.
3.Flavors,colors and normalization conditions
In the previous section,we examined the system of 5η particles in terms of color.Now,we wish to examine the same system in terms of flavor and then combine our results with the corresponding color probabilities we calculated earlier.After that,we convert the discrete system into a continuum density of states and,finally,obtain normalization conditions that will help us calculate system energies.
3.1.Counting based on flavors
Our multi-quark system consists of 5η particles,where η is the number of pockets.In each pocket there are four quarks and one antiquark.If NIandrepresent the number of flavors and the number of anti-flavors with degeneracy factors gIandrespectively,then,

where I=1 indicates light quarks and I=2 indicates heavy quarks.Degeneracy factors g andcan take on a value of one,two,three or four depending on whether it is a light or heavy quark,which will be further explained in the results.
3.2.Putting flavors and colors together
Since there are 4η quarks and η anti-quarks,we can expect 4η(4η−1)/ 2 interactions between colors,η (η −1) /2 interactions between anti-colors,and 4η2interactions between color and anti-color,all of which add up to 5η(5η −1)/2.Interactions between two flavors can only be either CCA or CCR type,interactions between two anti-flavors can only be either AAR or AAA,and interactions between a flavor and anti-flavor can only be CAR or CAA.Using the equations above,we can summarize the interactions as those shown in table 9.
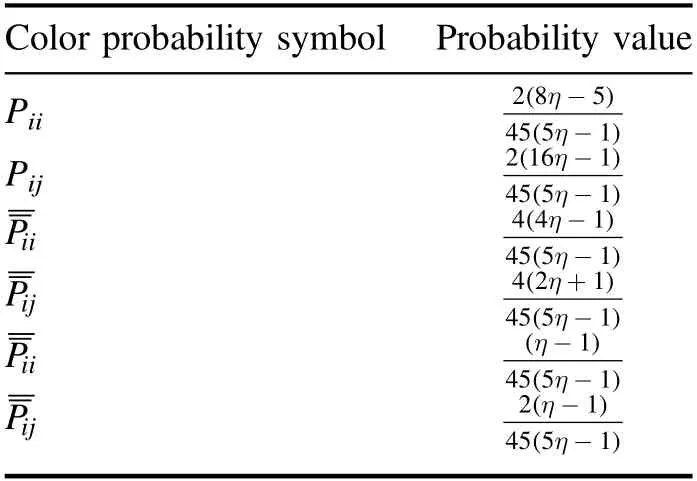
Table 8.Probabilities due to color interactions in multi-pentaquarks.

Table 9.Interactions due to flavor.
By assigning the flavors with color interaction probabilities,we can develop the expression for the potential energy.In the expression for potential energy in equation(26)of [15],there are terms related to CCR and CCA,terms for AAR and AAA,and one term for CAR and CAA type.They can simply be obtained by the expansion of the terms displayed above and separated into same flavor and different flavor pieces.
3.3.Discrete to continuum system
The system we have so far described has been one of discrete particles and,in order to apply the TF model,we have to convert it into a continuous system.Ifandrepresent quark density of particles and anti-particles with flavor index I and color index i,respectively,then equations (6) and (7) can be written as

and
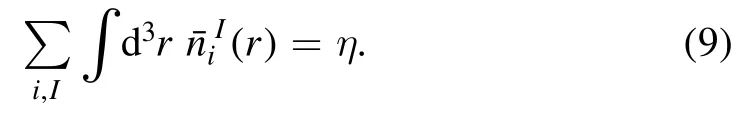
In the above equations,the degeneracy factors are already included in the quark densitiesandFor a particular color index i,the above equations can be written as,
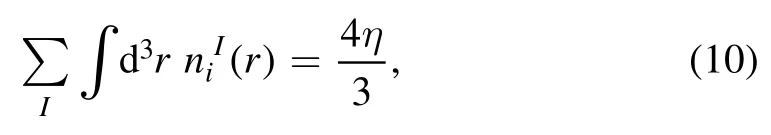
and
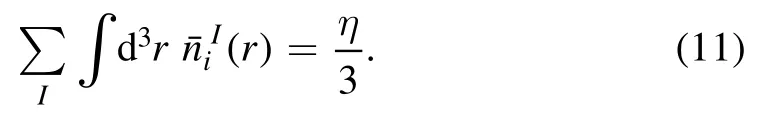
Similarly,for a particular flavor index I,these equations become

and

3.4.Fermi–Dirac normalization
For individual colors,equation (12) can be written as

We will assume equal quark color content and drop the index i from this equation,remembering to sum over colors later.This gives
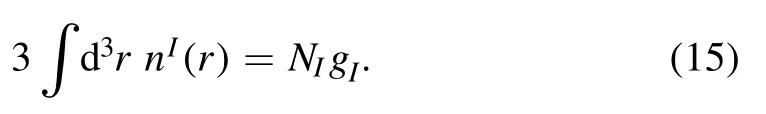
Similarly,for anti-particles,we have

We will now introduce TF functions,fI(r) andas
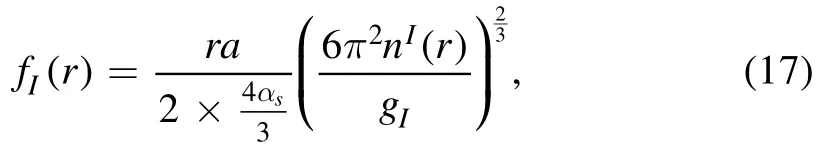
and
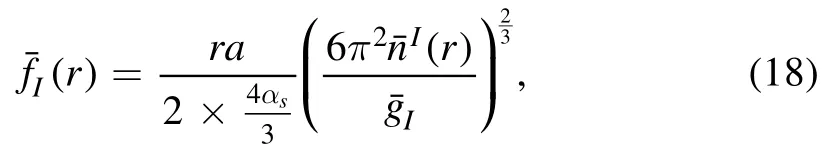
where a=ħ/(m1c) gives the scale,m1is the mass of lightest quark,and αs=g2/(ħc)is the strong coupling constant.Note that gIandare degeneracy factors.Equations(15)and(16)can now be written as
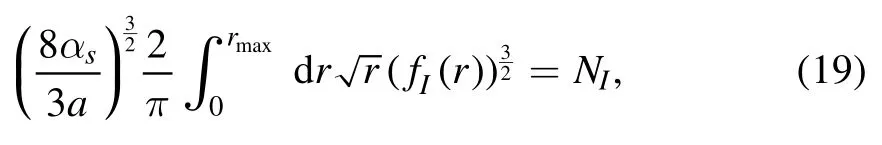
and

We will introduce a dimensionless parameter x such that r=Rx where

In terms of the dimensionless parameter x,equations(19)and(20) reduce to the following normalization conditions:
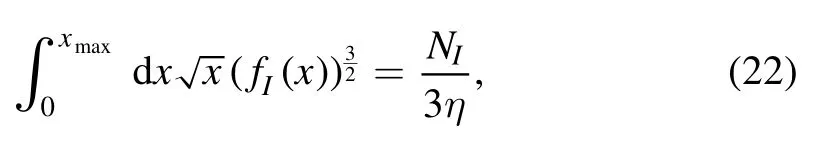
and
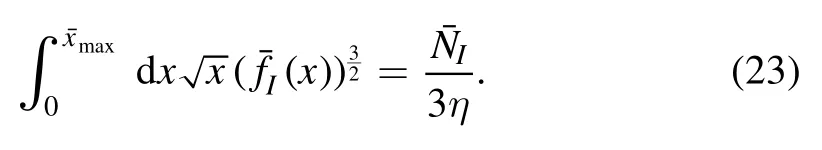
4.Expression for total energy
In this section,we first introduce the TF model to show how the kinetic and potential energies are expressed as a function of the density of states.We then use the interaction probabilities from previous sections to build the expression for the potential energy for a family of multi-pentaquarks.The TF Statistical model is a semi-classical model introduced to many fermion systems.It treats particles as a Fermi gas at T=0.Despite it utilizing Fermi statistics,it is not fully quantum mechanical since it does not have a quantum mechanical wave function but,rather,a central function related to particle density.This function is determined by filling states up to the Fermi surface at each physical location.The key idea of the TF quark model is to express both the kinetic energy and the attractive and repulsive potential energy contributions as a simple function of quark density.
The general expression for the kinetic energy is explained in section 2 of [15] and is embodied in equation (25)6Please note the incorrect numerator in equation (25) of [15].The correct numerators should replace the 6π2 factors with 2π2.This error propagates to equation (27),but no further.In addition,the kinetic energy terms in equations (28) and (31) should not have the number densities NI and in their numerators.This error also does not propagate.of that reference.In order to apply this expression to the quark system,we will introduce normalized degeneracy densitiesandgiven by

and

This new form of the quark density is helpful in correctly normalizing energies when continuum sources are used.When summed over flavors and colors,this yields the total kinetic energy (T)

The procedure for determining the potential energy (U) will mirror that of [15] in equation (26) with the exception of the new probabilities found for the multi-pentaquarks.We use the probabilities and flavor statistics of the previous section,giving

We have

and

Furthermore,with equal weighting provided to all the colors,we arrive at the final expression for the total energy (E)

where we have switched to the single-color particle densities nIandwith normalizations (15) and (16).
5.TF pentaquark equations
In section 4,we calculated the total energy of a family of pentaquarks.Now,we want to formally minimize the energy by varying the particle densities,while keeping the quark number constant.This will give us the differential equations we need to solve.
Let’s introduce Lagrange undetermined multipliers λIandassociated with the constraints

and
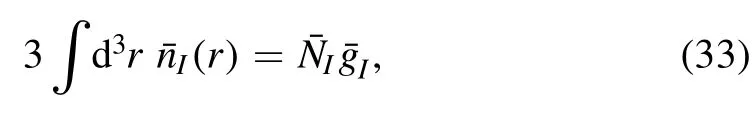
respectively.Then,the total energy becomes

Once again,the purpose of adding these terms involving the Lagrange multipliers is to allow a minimization of the total energy while keeping particle number fixed.
The variation of the density δnI(r)in equation(34)gives

Similarly,variation of the densityin equation (34)gives

We also know that
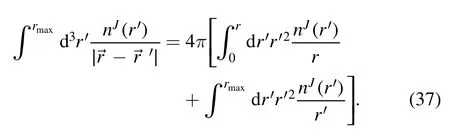
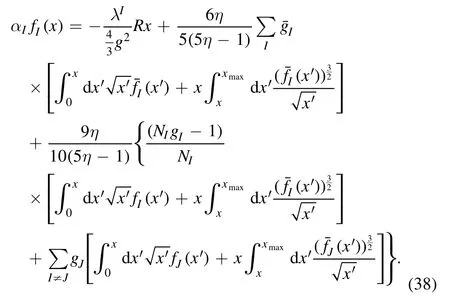
Differentiating equation(38)twice,we get the first of two TF differential equations,namely

Similarly,combining equations(17),(18),and(37)with(36)and using the dimensionless parameter x,we have
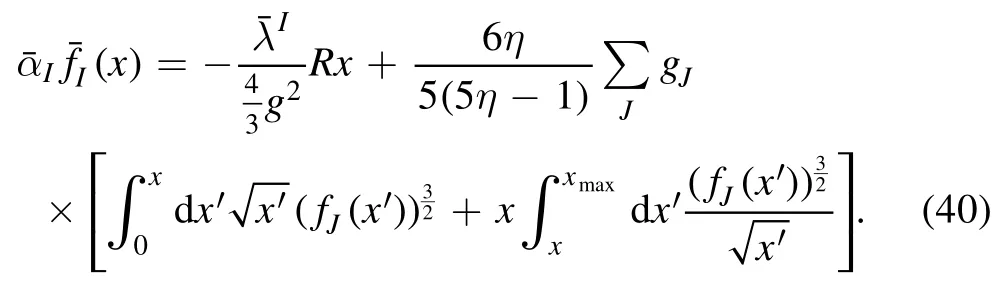
Finally,differentiating equation (40) twice yields

Equations (39) and (41) are TF differential equations for our system of pentaquarks.
6.Consistency conditions and parameters
Similar to the atomic model,the TF quark model assumes heavy particles in the central region and light particles spread outside of it.In the case of hidden charm multi-pentaquarks,the u and d quarks are light particles which can have larger radii while the c andare the heavy quarks relative to the u and d quarks.In this paper,we will be investigating whether the c or thewill be found within the innermost radius.This can depend on several factors like color-coupling probabilities,strength of color-coupling,separation between particles,number of flavors,mass of flavors,and more.
In this section,we first obtain the consistency conditions required for our model to give a single collective density of states and then discuss how the parameters will be chosen to solve consistency conditions numerically.
6.1.The consistency conditions
For the heavy particles,the TF function is f2(x) and for the heavy antiparticlesFor the light quarks,the TF function is f1(x) and for light anti-particles,Since we are not dealing with light anti-particles,will be zero.
The TF quark model creates a single,collective,spherically-symmetric density of states.So,we will assume that the TF Fermi functions of all particles will be linearly related to each other by some proportionality factor k and.In other words,

Using these TF functions in the TF differential equations,we obtain


and

Inserting equations (42) and(43)into equation (44)–(46),we obtain
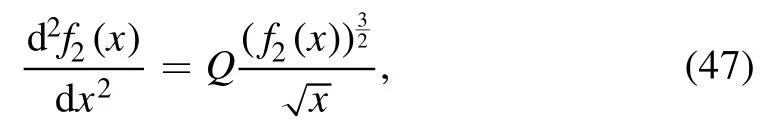
where
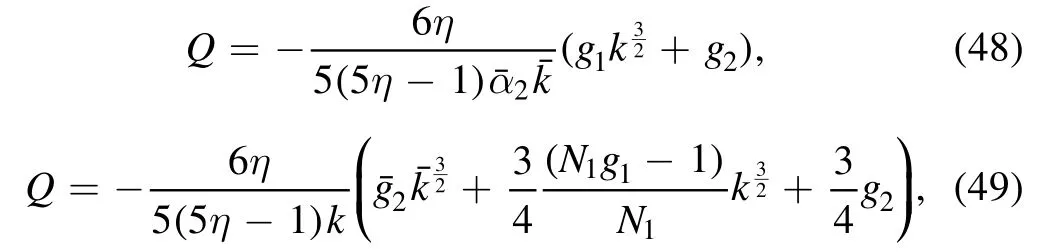
and

Equations(48)–(50)are the consistency conditions.Here,k,and Q are three unknowns which can be calculated using these three consistency conditions.
6.2.Methods and parameters
The internal number parameters which enter the model are the particle state numbers N1,N2and the antiparticle state numberIn addition,there are the particle and antiparticle degeneracy factors g1,g2andThese parameters satisfy the particle number constraints (6) and (7).Due to their masses being nearly equal,we will assume the density functions of the u and d quarks to be the same.Furthermore,since spin up and spin down states are distinguishable between flavors,this gives us four distinguishable particles with the same mass.The degeneracy factor,g1,for the light particle therefore will have a value from one to four.Charm and anti-charm can have a maximum degeneracy of two because there is no other quark with a similar mass.
In the following we will investigate the solution and interpretation of the consistency conditions in the special case of the ground state system for a given multi-pentaquark.We will therefore choose the maximum possible values for degeneracy factors g1,g2andfor each value of η.We will also specialize to the equal heavy state and number situation:N2=andg2=.Let us analyze the situation.
For η=1,the quark combination iscqqq,where q represents a light quark species.If one q is flavor u with spin up,another q is flavor u with spin down,and the last q is flavor d with either spin up or in spin down state,all three light flavors are distinguishable.Therefore,there should be a degeneracy of three for the light quarks.Similarly,c andcould either be spin up or spin down,so their degeneracy is one.Hence,we should have N1=1,g1=3,N2=1,g2=1,=1and,=1.For η=2,the quark combination is().In order to maximize the degeneracy factors,it is clear that the ground state is represented by N1=2,g1=3,N2=1,g2=2,=1and,=2.For η=3,the only state parameters which add up correctly are: N1=3,g1=3,N2=3,g2=1,=3,=1.For η=4,the maximum degeneracy state should haveg2==2.Then,maximizing the light quark degeneracy factor,we expect the ground state to be given by N1=3 and g1=4.For η=5 the only possibility is N1=5,g1=3,N2=5,g2=1,=5,and=1.Finally,for η=6,we have the maximally degenerate state N1=6,g1=3,N2=3,g2=2,=3and=2.
7.Results and discussion
The normalization condition from equations(22)and(23)can be written for heavy charm and anti-charm as
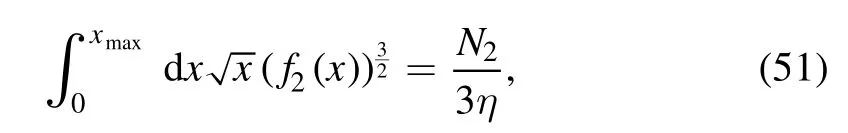
and

In the family of multi-pentaquarks under consideration,charm and anti-charm are always equal in number,henceN2=.If we assume thatwe may substitutefor all x in equation (52).Thus,we find

Since equations (51) and (53) have same right hand sides,it follows that the left hand sides should also be equal.Note that the functionis non-negative as it represents the number density and further that x,andxmaxare positive numbers.This implies that the value of integration keeps decreasing as the upper limit of integration decreases.In other words,ifthen consequently>1 and vice-versa as this argument can be repeated by substitution in(51)rather than (52).
We solved the consistency conditions given by equations(48)–(50)using Mathematica.We used the mass of charm and anti-charm from [15]; the masses of charm and anti-charm were 1553 MeV while the mass of the light quark was 306 MeV.We then obtained real values for k and,the results of which are tabulated in table 10 below.

Figure 1.For η=1,all three particles can be found inside the inner region represented by coordinate The middle region bounded by coordinate x2 is for heavy charm and light quarks but not anti-charm.The outer region between x2 and x1 is populated only by light quarks.
Table 10.Value of k and for various TF pentaquark states.
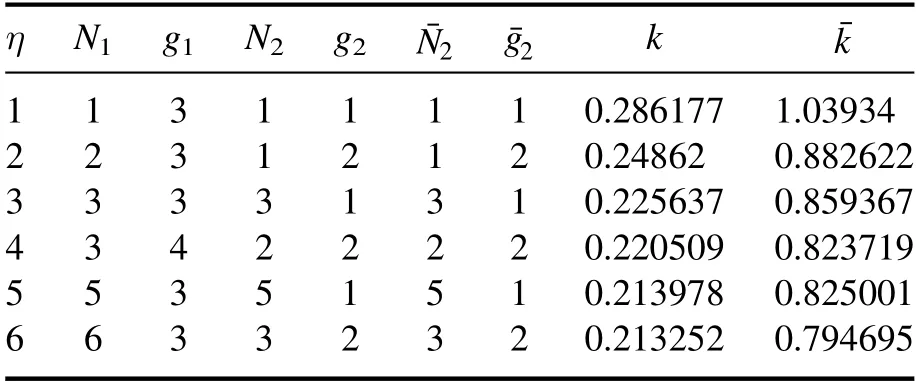
Table 10.Value of k and for various TF pentaquark states.
η N1 g1 N2 g2 ¯N2 ¯g2 k images/BZ_104_873_2510_901_2557.png 1 1 3 1 1 1 1 0.286177 1.03934 2 2 3 1 2 1 2 0.24862 0.882622 3 3 3 3 1 3 1 0.225637 0.859367 4 3 4 2 2 2 2 0.220509 0.823719 5 5 3 5 1 5 1 0.213978 0.825001 6 6 3 3 2 3 2 0.213252 0.794695
In our further investigations of this family of pentaquarks,we will need three TF functions for light quarks,heavy charms and heavy anti-charms.The position of x2andhave to be chosen carefully,depending on the number of quarks.Figures 1 and 2 illustrate the idea.
8.Future work

Figure 2.For η=(2,3,4,5,6) the region inside coordinate x2 is populated by all three particles.The middle region bounded by coordinate x2 and is for heavy anti-charm and light quarks but not charm.The outer region between and x1 is populated only by light quarks.
There are additional steps which need to be taken before the mass spectrum and radial structure of multi-pentaquark family states can be fully delineated.The complete kinetic and potential energies will need to be developed and related to the TF functions f1,f2andwith the understanding thatin general.The volume energy needs to be added and the numerical job of minimizing the total energy while solving the TF equations still remains to be done.
The beginning point for the phenomenology and fits in this model is the LHCb states identified as pentaquarks with minimal quark content;see the summary in [16].Note that a very simple model for hidden charm pentaquarks has a spin interaction Hamiltonian given by

where s1is the light quark spin,s2is the heavy quark spin and J is the total spin.The three terms represent the light–light,heavy–heavy and light–heavy spin interactions,respectively.We would expect that κ2<κ1,κ3based on the quark masses.It will be necessary to form a hypothesis on the spin and parity content of the LHCb pentaquark states in order to fit the model parameters,which include the charm and light quark masses,the strong interaction constant αsand the bag parameter,B.On the other hand,this process has already been completed in the considerations of[15],and we could proceed with the previous parameter set.Ideally,the use of two sets of parameters could give an indication of the systematic error in the model.In addition,to bring the evaluations to the same level of completeness as in [13,14],the spin energies also need to be calculated for the various degenerate states based upon their non-relativistic wavefunctions.
There have been model attempts to interpret pentaquarks as either a system made of diquarks [17] or triquarks [18,19],a loosely bound molecular model consisting of a charmed baryon and an anti-charmed meson[20],or compact hadro-charmonium states [21–24].Our statistical model does not assume smaller subsytems of quarks per se,but postulates that the interactions between the quarks can be characterized by averaged gluonic color interactions.In the emergent system formed the charmed and anti-charmed quarks reside at the center of the system,and in this sense more closely resembles the structure associated with the hadro-charmonium picture.However,note that equation(54)will produce a seven-plet of spin energy levels,the same as the molecular picture [25].Ultimately,it will be the the comparison with the pentaquark energy levels,which are nearparticle thresholds,which will be the most revealing.We now have all the tools to make this comparison:the baryon results from [13,14] (which need to be extended to charm quarks) and the meson results from [15] will allow us to calculate both thresholds and pentaquark energy levels when a unified set of parameters are used.We then use the reliable predictions from TF particle density theory as a basis to search for families of such states.The ground states will only be stable if the average energy per quark is a decreasing function of quark number.We have found such a decrease for a type of meson state that we called Case 2 charmed and bottom systems in[15].This is what we will search for in pentaquark families as well.
Although this represents a considerable amount of additional work,we are encouraged by the consistent mathematical structure and physical picture that seems to be emerging,and we pause here before continuing on.
9.Conclusions
We have initiated research into hidden charm multi-pentaquark families using the TF statistical model.We were able to evaluate the various color interaction terms and obtain the probabilities of particle and antiparticle interactions.This allowed us to form the kinetic and potential energies subject to flavor normalization conditions.We then obtained the appropriate TF differential equations and solved the consistency conditions for a number of multi-pentaquark ground states.We found that this required at least three TF functions with three different radii.We observed that for a pentaquark,the ordering of the quark radii is as in figure 1 where the heavy charm antiquark is limited to the innermost region.As the quark content increases,however,the heavy charm,rather than the anti-charm,is limited to the center region,as in figure 2.Our evaluations were carried out to η=6,i.e.for a state that is a combination of 6 pentaquarks.
Acknowledgments
We thank the Baylor University Research Committee,the Baylor Graduate School,and the Texas Advanced Computing Center for partial support.We would like to acknowledge Mr Sujan Baral and Ms Pratigya Gyawali,CEO and COO respectively from Everest Institute of Science and Technology for initiating EVIST research collaborations.We thank Mr Bikram Pandey,Mr Shankar Parajuli and Mr Pravesh Koirala for partial calculations and other helpful considerations.We also acknowledge the Grant Office at Niagara County Community College as well as the National Science and Research Society for Educational Outreach of Nepal.
杂志排行
Communications in Theoretical Physics的其它文章
- First-principles study on superconductive properties of compressive strain-engineered cryogenic superconducting heavy metal lead (Pb)
- Majorana–Kondo interplay in a Majorana wire-quantum dot system with ferromagnetic contacts*
- Effect of Zn doping on electronic structure and optical properties zincblende GaN (A DFT+U insight)
- Exploring the influence of microRNA miR-34 on p53 dynamics: a numerical study*
- A new approach for modelling the damped Helmholtz oscillator: applications to plasma physics and electronic circuits
- Coexistence and fluctuations phenomena with Davidson-like potentials in quadrupole–octupole deformed nuclei
