Analysis of the excited Ωc states as the pentaquark states with QCD sum rules
2021-04-12HuiJuanWangZunYanDiandZhiGangWang
Hui-Juan Wang,Zun-Yan Di and Zhi-Gang Wang
1 Department of Physics,North China Electric Power University,Baoding 071003,China
2 School of Nuclear Sicence and Engineering,North China Electric Power University,Beijing 102206,China
Abstract
Keywords: charmed baryon states,charmed pentaquark states,QCD sum rules
1.Introduction
In 2017,five new narrow excited Ωcstates named Ωc(3000),Ωc(3050),Ωc(3066),Ωc(3090) and Ωc(3119) were observed in the LHCb collaboration [1].These new observed hadrons were reported to be the excited states of Ωcwhich is composed of one c quark and two s quarks.The decay widths of these states were also measured,which were only a few MeV.However,the quantum numbers of theses excited states are not confirmed until now.
The above discovery inspired a large amount of theoretical studies of these excited Ωcstates with different asssumptions of their structures.Conventionally,these states were interpreted in three-quark frames [2–13] and assigned as the orbitally or radially excited states of the Ωcbaryons.In [9],the authors employed the QCD sum rules on the light-cone to study the decay properties of Ωcbaryons and assigned Ωc(3000),Ωc(3050)and Ωc(3119) to berespectively.In[10],the authors assigned Ωc(3066)and Ωc(3119)as the 2S states,and used the QCD sum rules to calculate the masses of these states.In[11],the authors employed the3p0model to study the decay widths of the charmed baryons and interpreted Ωc(3066) and Ωc(3090) to be 1P-wave withrespectively.The possibility of the assignment of the 1D-wave states were also discussed in[11].In[12],we assigned Ωc(3000)and Ωc(3119) to beandrespectively,and assigned Ωc(3090) to beorIn [13],our calculation predicted Ωc(3000),Ωc(3050),Ωc(3066),Ωc(3090)and Ωc(3119)to be the P-wave baryon states withandrespectively.
In 2015,the LHCb reported the exotic structure Pc(4450)which also has a narrow decay width of 39 ± 5 ± 19 MeV[14].In [15],the analysis of the low-lying pentaquark states with S=−3 and negative parity indicated that baryon excitation by pulling out apair may need less energy than by the tranditional orbital excitation.The ground states of Ωcare Ωc(2695)and Ωc(2770)with spin-parityandwhich had been observed experimentally.The mass gaps between the excited Ωcstates and the ground states are 230–424 MeV,which are large enough to excite a light quark-antiquark pair.It means these excited states can be the multiquark candidates.

Figure 1.The absolute contributions of the vacuum condensates of dimension n for central values dependent on the energy scalewhere (I) and (II) denotesusc andsusc,respectively,(a) and (b) correspond to respectively.
Kim et al proposed Ωc(3050) and Ωc(3119) to be exotic pentaquarks withrespectively,in the chiral quark-soliton model.The calculation of the strong decays of Ωc(3050)and Ωc(3119)supported the assignment and naturally explained the LHCb obsevation that Ωc(3050) and Ωc(3119)have anomalously small widths [16].In [17],the investigation found that the pentaquark configurations take sizable probabilities in these Ωcbaryons.Yang and Ping studied both the three-quark system with ssc and the five-quark system withandsscddby performing the dynamical calculation of Ωcin the framework of the chiral quark model[18].Those excited states were also considered as candidates of molecular states[19–21].In [22],we designed these excited states as axialvector-diquark-scalar-diquark-antiquark type charmed pentaquark states with.
In our previous work,we have ever assigned the five Ωcstates as conventional three-quark baryon states [12,13] and axialvector-diquark-scalar-diquark-antiquark type charmed pentaquark states [22].A hadron could have a lot of Fock states,which can couple to different interpolating currents with certain quantum numbers.Up to now,the mass spectrums of these Ωcstates were not determined,we can construct different three-quark and pentaquark interpolating currents to investigate the inner structures of these hadrons.In the present work,in order to explore the possible interpretation of pentaquark states for these Ωcstates,we construct both the scalar-diquark-scalar-diquarkantiquark type and axialvector-diquark-axialvector-diquark-antiquark type interpolating currents to study the charmed pentaquark stateswithBy considering the vacuum condensates up to dimension 13 we investigated the masses and pole residues of the charmed pentaquark states through the QCD sum rules.Comparing the results with the measurement of LHCb,it is found that the scalar-diquark-scalar-diquark-antiquark type and axialvector-diquark-axialvector-diquark-antiquark type charmed pentaquark stateswithcan be possible candidates of the excited Ωcstates observed in the LHCb collaboration.
2.QCD sum rules for the charmed pentaquark states
The two-point correlation function in QCD rum rules is written as follow

where

i,j,k,l,m,n and a are color indices,C is the charge conjugation matrix.In this work,we construct the scalar-diquarkscalar-diquark-antiquark type and axialvector-diquark-axialvector-diquark-antiquark type interpolating currents to study the charmed pentaquark stateswith.
At the phenomenological side,a complete set of intermediate pentaquark states with the same quantum numbers as the current operators J(x) and iγ5J(x) are inserted into the correlation functions Π(p) to obtain the hadronic representation [23].The result is obtained as follow after isolating the lowest states with.

where M±and λ±are the masses and the pole residues of the lowest states corresponding torespectively.
The currents J(0) couple potentially to the charmed pentaquark states with[24]

Based on dispersion relation,we can obtain the hadronic spectral densities at the phenomenological side
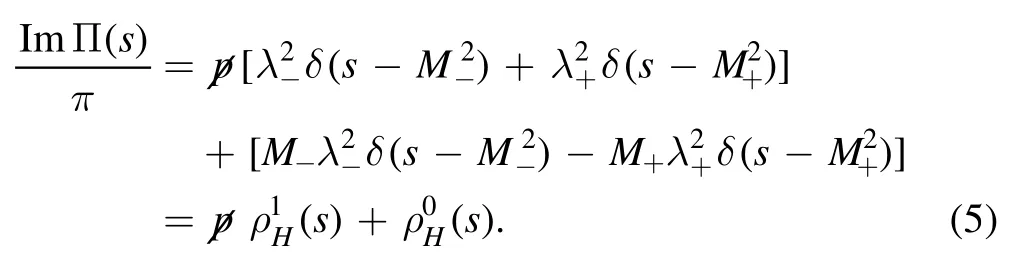
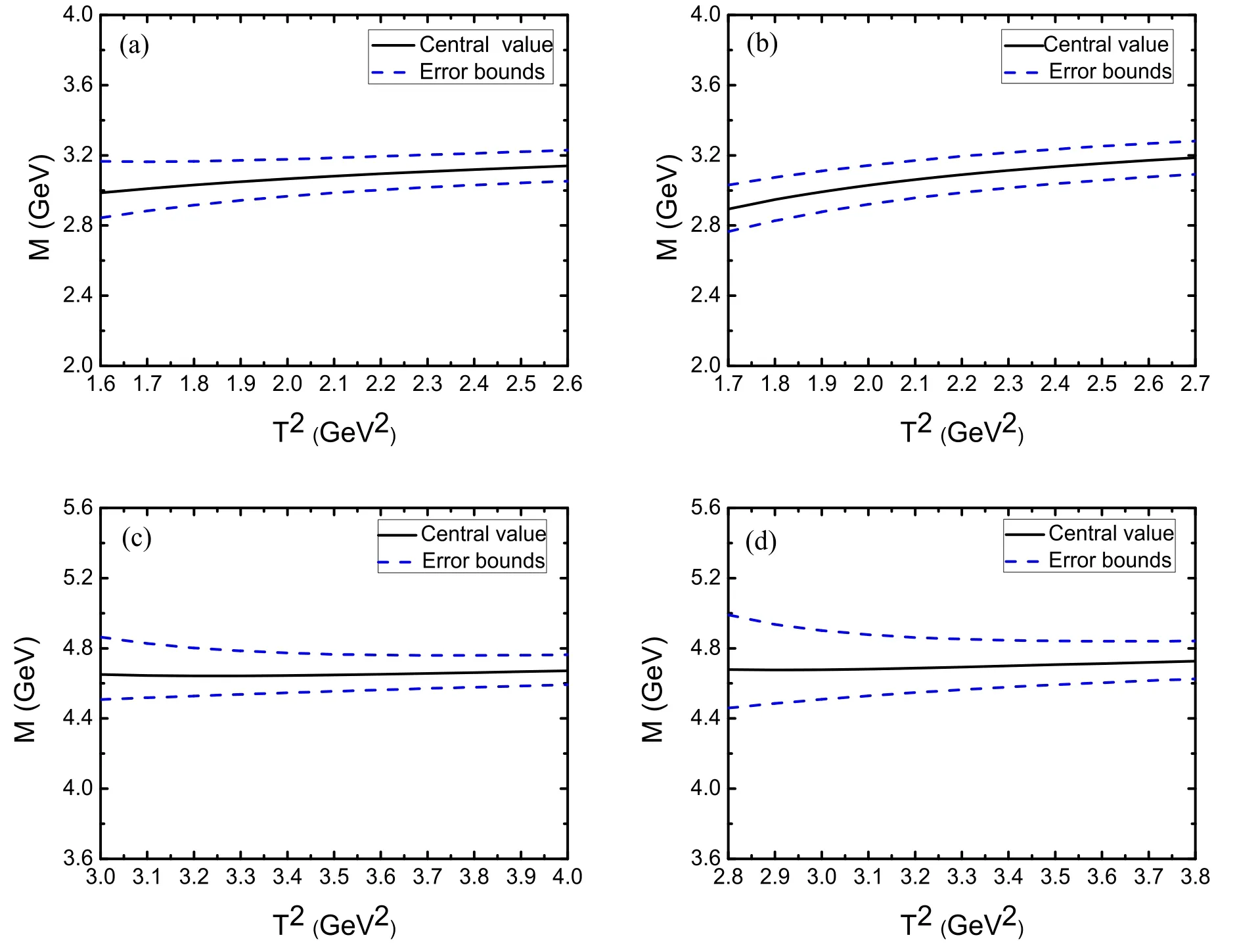
Figure 2.The masses of the charmed pentaquark states with variations of the Borel parameter T2 dependent on the energy scalehere (a)–(d) correspond tespectively.
We can obtain the QCD sum rules at the hadron side by introducing the weight function,

where the subscript H denotes the hadron side,s0is the continuum threshold parameter and T2is the Borel parameter[24].According to equations (5) and(6),we can separate the negative parity state from the positive parity state clearly.
We briefly outline the operator product expansion for the correlation functions Π1,2(p).Using Wick theorem we contract the s,u and c quark fields in the correlation function Π1,2(p) and obtain the results as follow:
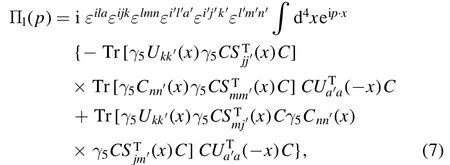
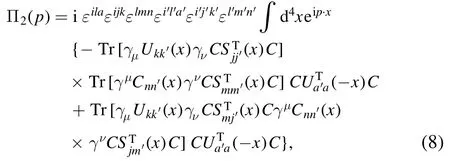
where Uij(x),Sij(x) and Cij(x) are the full u,s and c quark propagators,respectively [23]

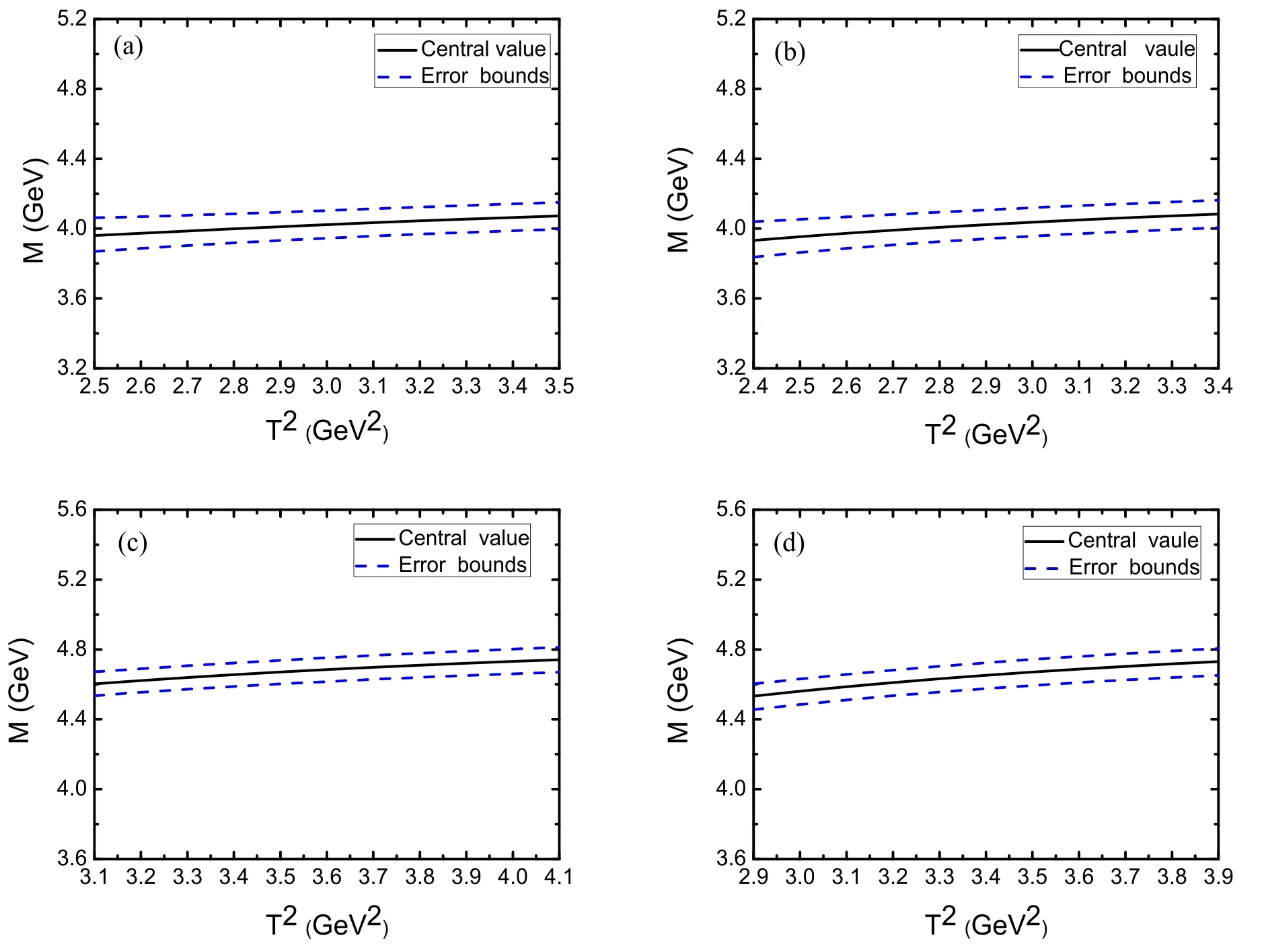
Figure 3.The masses of the charmed pentaquark states with variations of the Borel parameter T2 dependent on the enery scale μ=1 GeV,where (a)–(d) correspond to respectively.


After obtaining the QCD spectral densitiesandwe take the quark-hadron duality below the continuum threshold parameter s0and introduce the weight functionto obtain the QCD sum rules:
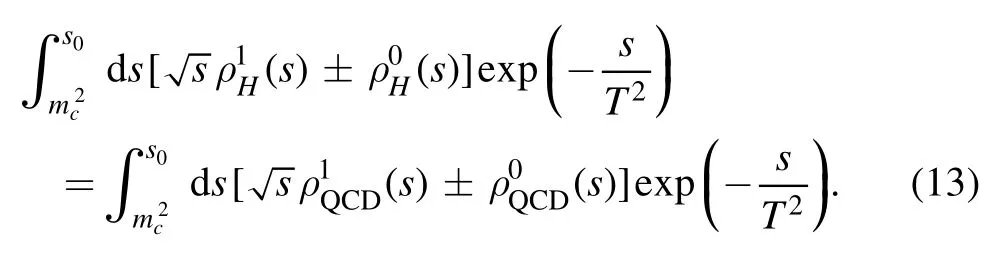
The QCD sum rules can be rewritten clearly as follow

We derive equation (14) with respect tothen eliminate the pole residues λ±and obtain the QCD sum rules for the masses of the charmed pentaquark states
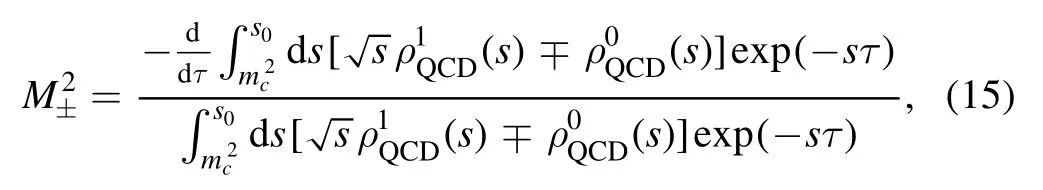

Figure 4.The masses of the charmed pentaquark states with variations of the Borel parameter T2 dependent on the enery scale μ = 1.0 GeV,where (a)–(d) correspond to and respectively.

Table 1.The optimal energy scale μ,Borel parameter T2,continuum threshold parameter s0 and pole contributions for the charmed pentaquark states.
where M±are the masses of the charmed pentaquark states withOnce the masses M±are obtained,we can take them as input parameters and obtain the pole residues from the QCD sum rules in equation (14).
3.Numerical results and discussions
In our calculation,the vacuum condensates values are taken as−(0.24 ±0.01 GeV)3,=(0 .33 GeV)4at the energy scale μ=1 GeV[23],The quark condensate and the mixed quark condensate evolve with the renormalization group equation [28,29]
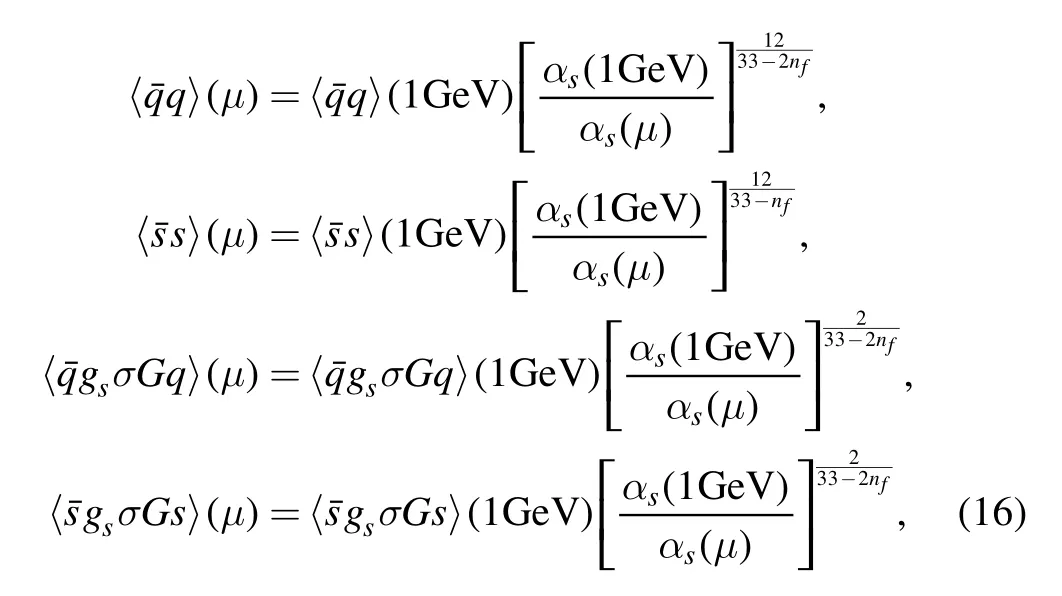
here,we choose the MS masses mc(mc)=(1.28 ± 0.03)GeV andms(μ= 2 GeV) = 0.096GeV from the Particle Data Group[30].Furthermore,we take into account the energy-scale dependence of themasses from the renormalization group equation
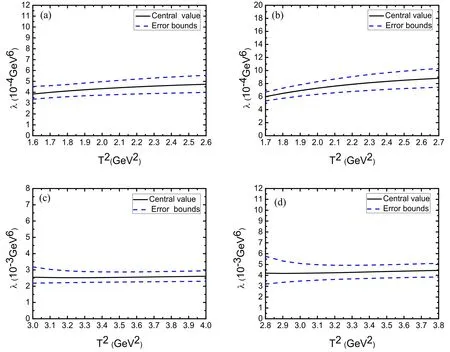
Figure 5.The pole residues of the charmed pentaquark states with variations of the Borel parameter T2 dependent on the energy scalewhere (a)–(d) correspond to respectively.

We have ever discussed how to choose the optimal energy scale and suggested an energy scale formulato study hidden charmed(bottom)tetraquark states,pentaquark states and molecular states in the QCD rum rules in details [24–27].The effective Q-quark massesMQembody the net effect of the complex dynamics and have universal values[24–27].In this paper,we rewrite the energy scale formula asbecause there exists only one c quark,and take the effective c-quark mass Mc=1.82 GeV [33].
Here,we study the charmed pentaquark states with three types of energy scale parameters.Firstly,we evolve the input parameters to the energy scaleto extract the masses MP.Then,we evolve the input parameters to the energy scale μ=1 GeV to extract the masses MP[34,35].Finally,we evolve the input parameters except for mc(mc) to the energy scale μ=1GeV to extract the masses MPwhich is denoted asμ=GeV [36,37].
We can determine the ideal Borel parameter T2and continuum threshold parameter s0according to three criteria.The first criterion is pole dominance at the hadron side.The optimal energy scale μ,ideal Borel parameter T2,continuum threshold parameter s0and pole contribution are shown in table 1.From table 1,we can see that the pole contributions are approximately in the range of 40%–60% and pole dominance at the hadron side can be satisfied.The valuescan lead to satisfactory results [38–40].In this work,the pole contributions PC is defined as follow

Figure 6.The pole residues of the charmed pentaquark states with variations of the Borel parameter T2 dependent on the enery scale μ=1 GeV,where (a)–(d) correspond to respectively.

here,‘+’ and ‘−’ correspond to the pole contributions for negative parity state and positive parity state,respectively.
The second criterion is convergence of the operator product expansion.The absolute contributions of the vacuum condensates |D(n)| for the central values dependent on the energy scale parameterare shown in figure 1.D(n) is defined as

where ρn(s) is the n dimension QCD spectral density,andis the total spectral density.In this work,we carry out the operator product expansion up to the vacuum condensates of dimension 13 and assume vacuum saturation for the higher dimension vacuum condensates.We take the truncations n≤13 and k≤1 in a consistent way anddiscard the operators of the orderswith k>1 [22].From figure 1,we can see that the largest contribution comes from the vacuum condensates of dimension 6 for the scalardiquark-scalar-diquark-antiquark type pentaquark state denoted aswith negative parity.The contributions from dimensions 10,11,12 and 13 are tiny.Therefore,the operator product expansion is convergent in this case.The axialvectordiquark-axialvector-diquark-antiquark type pentaquark state denoted aswith negative parity has the analogous situation.For the positive parity pentaquark states,the dominant contributions come from the perturbative terms,the operator product expansion is obviously convergent.For another two kinds of energy scale parameters,the convergence of the operator product expansion is also satisfied.
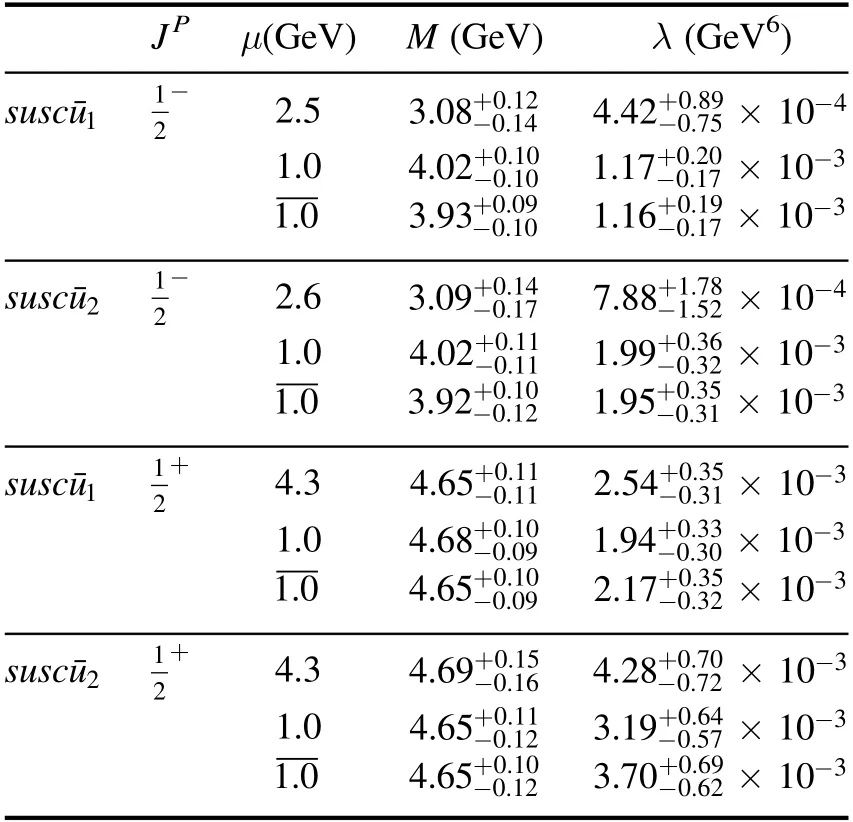
Table 2.The predicted masses and pole residues of the charmed pentaquark states.

Figure 7.The pole residues of the charmed pentaquark states with variations of the Borel parameter T2 dependent on the enery scale μ = GeV,where (a)–(d) correspond to respectively.
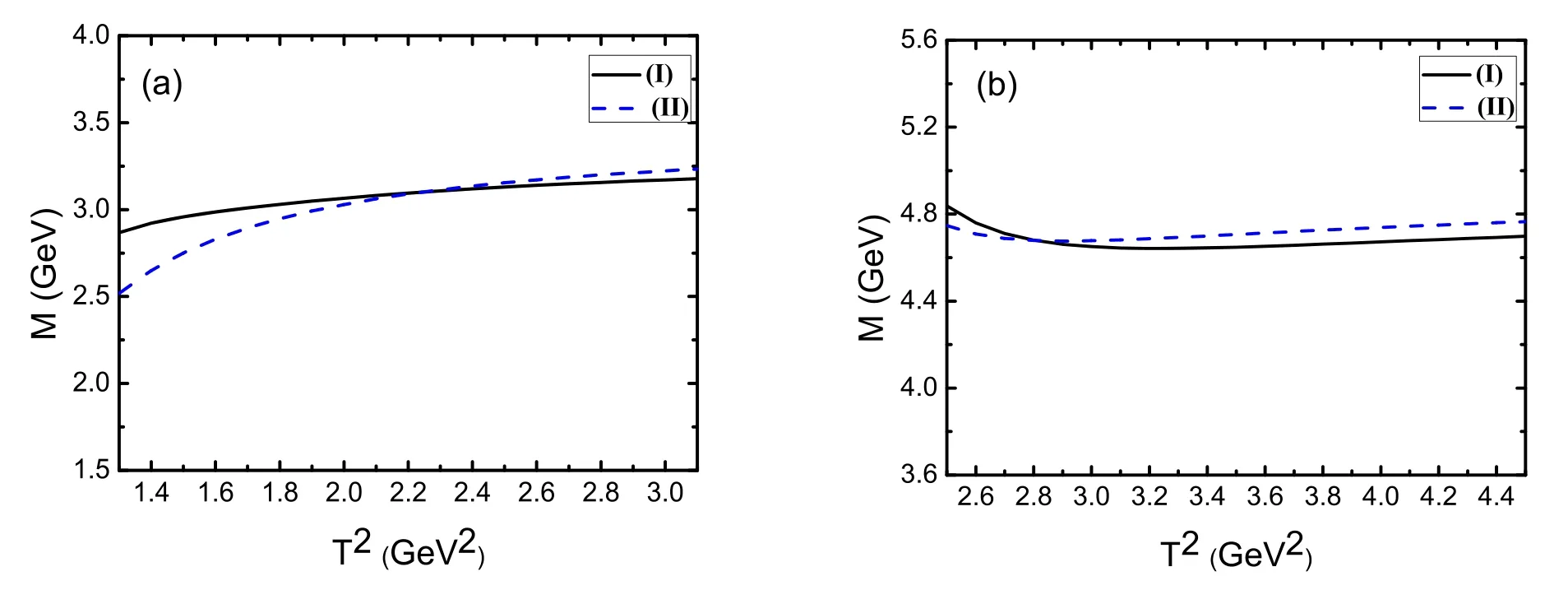
Figure 8.The predicted masses with variations of the Borel parameter for central values dependent on the energy scale μ = where (I) and (II) denote the pentaquark statesand,respectively,(a) and (b) correspond to and respectively.
The third criterion is Borel platforms figures 2–7 show the masses and pole residues distribution with the variations of the Borel parameter T2at much larger intervals than the Borel windows as shown in table 1.It can be clearly seen that the uncertainties of the masses and pole residues from the Borel parameter T2in the Borel windows are very small,therefore,the Borel platforms exist.Now the three criteria are all satisfied.
Figure 8 shows the masses distribution with the Borel parameter for central values on a large scale dependent on the energy scaleIt is seen that the predicted masses increase slowly with the Borel parameter for the negative parity.For the positive parity the predicted masses decrease slowly with the Borel parameter.It warrants the appearance of good Borel platforms.
Considering all uncertainties of the parameters,we obtain the masses and pole residues of the charmed pentaquark states withbased on three types of energy scale parameters as shown in table 2.It is seen that the predicted masses of the charmed pentaquark statesandwithdependent on the energy scale parameterareandrespectively,which are in consistent with the experiment data of the LHCb collaboration [1].The masses of the charmed pentaquark statesandwithdependent on the energy scale parameterareandrespectively,which have large deviation to the five new excited states.The predicated masses based on the other two kinds of energy scale parameters are larger than that based on the energy scale formula.
The predicted uncertainties originate from the input parameters,such as the effective c-quark massMc,the continuum threshold parameter s0,and the vacuum condensate valuesand,in which the parameters s0andcause main uncertainties.For example,for the charmed pentaquark stateswiththe uncertainties from s0andareandrespectively.
From table 2,we can see that the masses of the negativeparity pentaquark states from two different interpolating currents lie in the same region.Generally speaking,an interpolating current can couple to a hadron or several hadrons or a hadron system or several hadron systems if they have the same quantum numbers,as the non-vanishing couplings are not forbidden by the symmetries.On the other hand,a hadron maybe have many Fock states,a Fock state couples potentially to an interpolating current with the same quantum numbers as the Fock state.Therefore,the present calculations could indicate that a pentaquark state owns two different inner structures,or two pentaquark states have masses in the same region.More experimental and theoretical works are still needed to make a solid assignment.In addition,it is found that the mass gaps between the positive-parity pentaquark states and the corresponding negative-parity pentaquark states are more than 1.5 GeV.If the positive-parity pentaquark states are the orbitally excited states of the negative-parity ones,the mass splittings seem too large because the energy costs exciting an orbital angular momentum are approximately 300–600 MeV.However,our calculation results are obtained based on the quantum chromodynamics,which are different from the ones based on the quark model,the positive-parity pentaquark states are not necessarily the orbitally excited states of the negative-parity ones.The currents J1(x) and J2(x) have negative-parity,they also couple potentially to the positive-parity pentaquark states,as multiplying iγ5to the currents to change their parity[40–43].
For the positive-parity pentaquark states,the contribution of the vacuum condensate of dimension n in the QCD spectral densitywith n≥3 is canceled out with the corresponding ones in the QCD spectral densityto a great extent due to the combinationthe operator product expansion converges very well at all the energy scales μ≥1 GeV.In such a case,the energy scale formulacan only improve the pole contributions mildly and enhance the operator product expansion convergence mildly,therefore the predicted pentaquark masses depend on the energy scales of the QCD spectral densities mildly.For the negative-parity pentaquark states,the contribution of the vacuum condensate of dimension n in the QCD spectral densitywith n≥3 is strengthened by the corresponding ones in the QCD spectral densitydue to the combinationthe operator product expansion converges very slow.In this case,the energy scale formulacan improve the pole contributions remarkably and enhance the operator product expansion convergence remarkably,we prefer the energy scale formulato choose the best energy scales of the QCD spectral densities to obtain the ideal Borel windows to extract the pentaquark masses,as the predictions vary considerably with variations of the Borel windows.
4.Conclusion
In this work,we construct both the scalar-diquark-scalardiquark-antiquark type and axialvector-diquark-axialvectordiquark-antiquark type interpolating currents to study the charmed pentaquark stateswithWe employ three types of energy scale parameters to investigate the masses and pole residues of the charmed pentaquark states using the QCD sum rules.By comparing these results with experiment data,we find that if we take pole contributions in the scope of 40%–60%we can get more reasonable prediction using the energy scale formulathan the other two types of energy scale parameters.The energy scale formulacan improve the pole contributions dramatically and enhance the operator product expansion convergence remarkably,especially for the negative parity states.Hence,we prefer the energy scale formulain this work.Our calculation results support assigning the new excited Ωcstates to be the scalar-diquarkscalar-diquark-antiquark type and axialvector-diquark-axialvector-diquark-antiquark type charmed pentaquark stateswithIt indicates that the pentaquark configuration can be possible interpretation of the new narrow excited states observed in the LHCb collaboration.
We group the flavor parts asto construct the interpolating currents here.If we group the flavor parts asto construct the scalar-diquark-scalardiquark-antiquark type interpolating current,which is nonexistent according to fermi statistics.We can construct axialvector-diquark-axialvector-diquark-antiquark type interpolating current by grouping the flavor parts asThe result should approximately equal to that by grouping the flavor parts asaccording to the SU(3) symmetry.Further calculation is still needed to make a solid conlcusion.
Acknowledgments
This work is supported by National Natural Science Foundation,Grant Number 11775079.
Appendix








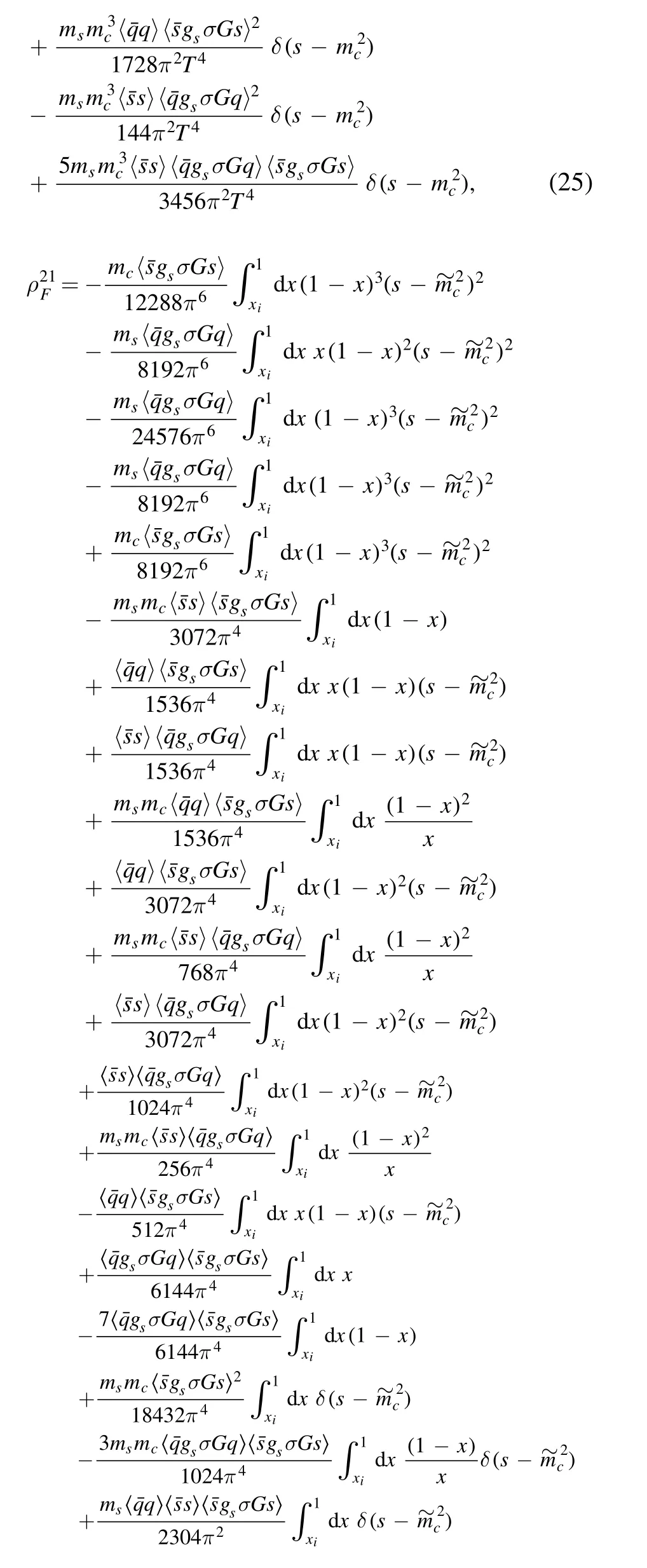


杂志排行
Communications in Theoretical Physics的其它文章
- First-principles study on superconductive properties of compressive strain-engineered cryogenic superconducting heavy metal lead (Pb)
- Majorana–Kondo interplay in a Majorana wire-quantum dot system with ferromagnetic contacts*
- Effect of Zn doping on electronic structure and optical properties zincblende GaN (A DFT+U insight)
- Exploring the influence of microRNA miR-34 on p53 dynamics: a numerical study*
- A new approach for modelling the damped Helmholtz oscillator: applications to plasma physics and electronic circuits
- Coexistence and fluctuations phenomena with Davidson-like potentials in quadrupole–octupole deformed nuclei
