基于接触理论与数值分析下复合墙体抵抗冲击力研究

邹佳明,杨伟军,夏彬华,杨春侠

(长沙理工大学,湖南 长沙 410004)

0 引言

近年来，我国装配式建筑行业技术发展迅速，特别是在建筑隔墙墙体创新及应用方面尤其显著。本文以一种新型的可调式轻质复合保温墙体为主要研究对象进行拓展，对建筑隔墙领域中出现的工程问题进行思考与探究，复合墙体如图1所示。

图1 可调式轻质复合保温墙体示意图

研究发现，建筑内隔墙复合墙体在使用期间会受到来自墙体外部物体的偶然碰撞，碰撞产生的冲击力会使墙体产生一定的局部变形或应力集中现象从而影响到墙体的各方面性能。从实际工程角度来看，建筑内的复合墙体受到来自物体低速碰撞的情况较多，产生的冲击作用的持续时间往往不长，产生的冲击大小则成为影响到复合墙体变形情况的主要因素之一，对于研究复合墙体抗冲击性能、安全设防、隔墙墙体结构设计等问题，如何确认这种低速碰撞后产生的冲击力大小则成为解决问题的关键因素之一。

通过对相关文献资料与现有的多种理论计算方法进行研究分析，认为采取能量守恒定律计算复合墙体受到物体碰撞后产生的最大冲击力较为符合实际[1]。为更贴合真实作用情况，采用将《建筑隔墙用轻质条板通用技术要求》[2]中的砂袋试验方法改进并简化来模拟复合墙体的受到物体的碰撞情况。

本文以如何计算墙体受到物体低速碰撞后产生的最大冲击力为主要研究内容，对于墙体受到物体低速碰撞下的状态展开墙体碰撞机理分析，采取分级评估方法对墙体破坏形态进行分析研究。当前冲击力的主要计算理论之一便是Hertz弹性碰撞理论[3]，对物体低速碰撞复合墙体后产生的冲力大小开展理论分析。基于考虑Hertz弹性理论和Thornton弹塑性理论[4]，假定砂袋落物满足Von Mises屈服准则的条件[5]，考虑碰撞面弹塑性区域的接触特性，通过简化计算模型推导考虑弹塑性变形的冲击力算法，提出适用于复合墙体的冲击力理论计算公式，并采用ABAQUS有限元数值模拟来验证模型与算法的有效性，以期解决复合墙体受到物体低速碰撞下产生的变形等问题来为实际工程推广应用提供理论依据，推进建筑隔墙结构设计的发展。

1 物体低速碰撞复合墙体下墙体破坏分级评估与机理分析

通过对相关文献与资料的研究发现我国建筑内复合墙体以采用混凝土材料作为墙体内部填充材料的情况居多。由于混凝土的抗拉强度较低，复合墙体受到外部物体碰撞后，产生贯通裂纹成为主要破坏形式之一[6]。

本文采用分级评估方法对复合墙体受到物体低速碰撞后产生的破坏形态进行研究分析。将复合墙体受到低速碰撞后的破坏部分分为单侧面板、泡沫混凝土、整体结构3个分析对象进行探究，其中整体结构指的是泡沫混凝土层与两侧面板共同组合而成的构造部分。复合墙体受到物体碰撞后形成的墙体破坏形式呈裂纹扩展、局部破坏、整体破坏3类主要形式[7]，结合实际碰撞情况，复合墙体的破坏分级如图2所示评估。

图2 受碰撞下复合墙体破坏分级评估图

以单侧面板为破坏对象进行破坏形式机理分析，在碰撞作用下单侧面板破坏形式可分为3类形式评估，①即裂纹扩展：单侧面板上裂纹宽度达到相关规范中的宽度限度之前的面板变形状态；②局部破坏：单侧面板在碰撞接触区域产生较大的冲切弯曲变形而未达到面板抗拉极限的破坏情况；③整体破坏：单侧面板整体变形达到面板的抗拉极限强度后弯曲破坏。

复合墙体内层的泡沫混凝土破坏形式同理采用分级评估进行破坏机理分析，①裂纹扩展：泡沫混凝土层受到来自物体碰撞后产生的裂纹在达到相关规范中的宽度限度之前的变形情况；②局部破坏：泡沫混凝土层受到来自物体碰撞后局部碎裂破坏；③整体破坏：泡沫混凝土层达到其抗拉极限后产生弯曲破坏。

以整体结构为对象采用3类评估形式分析，①裂纹扩展：复合墙体非碰撞一侧的面板上裂纹宽度在达到相关规范中的宽度限值之前的变形状态；②局部破坏：整体结构的非碰撞一侧的面板上裂纹宽度超过相关规范中的宽度限值但面板变形未达到抗拉极限时的状态；整体破坏：③整体结构受到物体碰撞后发生的整体变形达到屈服后产生整体弯曲破坏。

通过分级评估方法发现不同程度的破坏情况下，复合墙体接触面的受力情况也不同。对碰撞后的破坏机理分析得知复合墙体受到物体碰撞后的受力形式复杂，破坏形式多样，为得到复合墙体受到物体低速碰撞后产生的最大冲击力，本文以较为符合实际的情况对复合墙体受到外部物体低速碰撞后产生的冲击力进行理论计算研究。

2 复合墙体受外部物体低速碰撞产生的冲击力理论计算分析

2.1 动量与能量守恒分析

为较好地模拟复合墙体在正常使用过程中受到的碰撞现象，采取砂袋碰撞模式用于复合墙体受到物体低速碰撞后产生的冲击力理论研究。通过将规范砂袋试验中碰撞墙体的形式改进简化，依据能量守恒定律进行动力过程分析[8]，在不考虑下落过程中的能量损失，忽略空气与砂袋的摩擦阻力，假定砂袋重力势能全部转化为动力势能，得到如下转化关系式：

(1)

式中：m为砂袋质量，kg；H为砂袋初始高度，m；h为下落高度，m；v1为砂袋初速度；v2为砂袋碰撞到墙体上的瞬时速度；g为重力加速度，m /s2。

将式(1)简化得到能量转化式:

(2)

式中：符号说明同前。

2.2 动量定理与冲量平衡分析

由于对象为低速运动物体，依据动量守恒定律[9]，砂袋动量变化可表示如下：

ΔP=p′-p=mv2-mv1

(3)

式中：ΔP为动量变化量，kg·(m/s)；p′为末动量，kg·(m/s)；p为初始动量，kg·(m/s)；其余符号说明同前。

物体动量的增量变化等于物体所受合外力的冲量，结合冲量定律可知冲量是力在时间上的积累效应[10]，分析得到如下关系式：

FΔt=ΔP

(4)

通过将式(4)代入式(3)化简可得墙体接触面上的冲击力与砂袋物体的动量转化关系式：

FΔt=m(v2-v1)

(5)

式中：F为作用于墙体的冲击力，N；Δt为冲击力的作用时间，s；其余符号说明同前。

2.3 基本理论计算结果分析

以上公式算法是建立在能量守恒理论、冲量定理、牛顿第二定理[11]等理论基础上来求解复合墙体接触面上的最大冲击力。

研究分析发现，由于没有考虑复合墙体的整体变形和局部变形、砂袋碰撞产生的压缩变形和能量消耗等方面因素的影响，通过上述基本理论分析得到的式(5)计算得出碰撞接触面的冲击力值大于真实值。因此为更精确的求解实际冲击力，需考虑物体与复合墙体碰撞接触区域的弹塑性变形与摩擦产生的能量损失。

3 基于考虑弹塑性含修正参数的最大冲击力理论计算

3.1 基本假定与弹性分析

为得出物体低速度碰撞复合墙体后墙体的变形与冲击力之间的关系，本文将砂袋简化为一个球体，取复合墙体面板中心为最不利位置。假设砂袋与复合墙体的碰撞满足Hertz接触理论基本条件与下列基本假定：① 墙体接触面看作半无限空间；② 墙体均质连续且各向同性；③ 砂袋不转动；④ 砂袋为均质规则球体；⑤ 砂袋下落的速度方向垂直于墙体面板。

在墙体接触面产生塑性变形之前为完全弹性接触的前提下，弹性接触压力Pe与法向变形压缩量δ在弹性范围内之间的关系为：

(6)

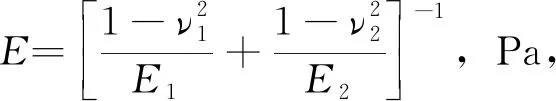
3.2 简化模型计算研究

在考虑弹塑性变形的影响，假定质量为m的匀质砂袋以速度v2撞击墙体，复合墙体受到碰撞后会产生一部分弯曲变形能[12]，通过对碰撞计算模型进行简化，将墙体简化为长a宽b厚h的墙板，如图3所示。

通过碰撞简化计算模型可知墙体抗弯刚度满足下列关系式：

(7)

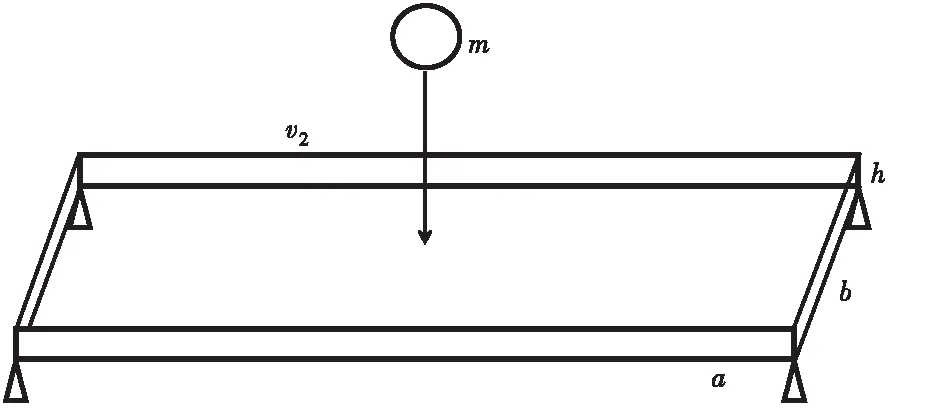
图3 复合墙体简化计算示意图

式中：D为墙板的抗弯刚度；h为墙板厚度，m；其余符号说明同前。

碰撞产生的冲击力转化为接触压力作用于墙体，通过弹性力学相关公式可知墙体所产生的弯曲变形能满足式(8)。

(8)

式中：Ew为墙体所产生的弯曲变形能；P为作用于墙体的接触压力，N；a为墙体面板长度，m；b为墙体面板宽度，m；其余符号说明同前。

基于Hertz弹性碰撞模型与理论，在假定两相互碰撞物体的接触面半径为r*前提下，可知碰撞时的弹性接触压力、接触变形量、接触面半径与接触压应力的关系如下：

(9)

砂袋与墙体的接触面半径与等效半径、法向变形压缩量关系满足式(8)。

(10)

3.3 基于Thornton弹塑性分析冲击力

由Thornton弹塑性假设可知，当最大接触压应力大于碰撞对象的屈服强度时，接触面上会产生一塑性变形区。不考虑碰撞对象的材料塑性硬化或软化并视其为理想弹塑性材料，通过式(6)、式(9)与式(10)联立求解得出屈服压应力与初始屈服对应的接触面半径之间的关系满足：

(11)

式中：py为碰撞接触面塑性区内的接触屈服压应力，MPa；ry为初始屈服对应的接触面半径，m；其余符号说明同前。

根据Hertz接触理论，假设砂袋屈服满足Von Mises屈服准则条件，可得到碰撞接触面塑性区内的接触屈服压应力的计算公式满足下式[13]：

py=CνY

(12)

式中：Y为接触材料的屈服强度，MPa。Cν=1.234+1.256ν，其中ν为接触材料的泊松比；

由式(9)至式(12)联立可知初始法向屈服压入变形量δy，再代入式(6)可得到初始法向屈服压力Py。弹塑性法向接触压力与法向压缩变形量之间关系满足下式[14]：

Pep=Py+2πRpy(δ-δy)

(13)

通过对能量守恒分析可知砂袋产生的动能主要由接触区域的局部弹性变形能、弹塑性变形能与墙体整体弯曲变形能组成，将式(8)代入能量守恒式，对等式积分可得到考虑弹塑性变形下法向最大压入量δmax满足式(14)。

(14)

式中：δmax为考虑弹塑性变形下法向最大压入量，m；其余符号说明同前。

由式(14)可知δmax，再将δ=δmax代入式(13)可知考虑弹塑性最大冲击力满足式(15)。

Pmax=Py+2πRpy(δmax-δy)

(15)

式中：Pmax为考虑弹塑性碰撞最大冲击压应力，kPa；其余符号说明同前。

3.4 含参数的修正表达

考虑复合墙体受到外部物体低速碰撞问题的特殊性，此问题包含弹塑性变形过程与粘性和摩擦能量耗散等行为，认为碰撞后产生的最大冲击力理论上应受到折减系数的影响，考虑弹塑性的最大冲击力应满足式(16)[15]。

Fmax=γPmax=γ[Py+2πRpy(δmax-δy)]

(16)

式中：Fmax为考虑弹塑性含修正参数的最大冲击力，N；γ为参数折减系数，依据相关文献与试验数据认为范围取0.85～0.95；其余符号说明同前。

4 冲击力计算公式适用与算例分析

4.1 适用分析

对于本文提出的计算公式的适用范围，进行分层次法分析。

复合墙体有其特殊的构造特征，通过对墙体受碰撞后的破坏形式进行分层次分析：将复合墙体的单侧面板受到碰撞后发生的弯曲破损视为复合墙体表观破坏，影响墙体的外观，通过面板裂纹扩展宽度判断。将泡沫混凝土内层受到碰撞后产生的弯曲破损开裂视为内部破坏，直接影响隔墙使用性能，通过泡沫混凝土抗弯屈服极限判断。

本文论述的理论计算方法主要适用于简化后的计算模型且面板厚度较薄的复合墙体。对不同层次的适用情况视复合墙体面板厚度而定。

4.2 工程应用算例分析

通过下列工程实际试验算例对理论计算方法进行应用和说明。

以复合墙体为碰撞接触对象，算例计算材料参数如表1所示。

表1 算例计算基础参数Table 1 Calculation of base parameters项目形状尺寸/mm泊松比计算参数/MPa复合墙体长方体1 200×600×2000.3弹性模量7 750简化后的标准砂袋球体直径2500.3弹性模量55

以考虑弹塑性含参数计算方法为例，给定重30 kg砂袋初速度为零，下落高度为1 m，以4.42 m/s速度碰撞墙体，动接触作用时间0.001 s，接触等效刚度E为3.5 MPa，通过式(12)计算得初始屈服强度py为0.148 MPa，结合式(10)与式(11)得到初始接触压入深度约为0.53 mm，代入式(14)与式(15)计算得到冲击力值约为7.31 kN。同不含参数的弹塑性理论计算与动能量守恒理论比较，如表2所示。

表2 冲击力计算值比较 Table 2 Comparison of calculated values of impact force理论计算方法运用公式计算结果/kN动能量守恒理论式(5)13.26考虑弹塑性接触理论式(14)、式(15)8.25含参数修正后计算式(16)7.31

表2为3种计算方法的比较分析，结果表明含参数修正的算法计算得到的结果更符合真实情况。

5 ABAQUS有限元数值模拟验证

5.1 有限元模型建立材料属性与本构选择

本文基于ABAQUS有限元建立复合墙体碰撞模型，数值模型由整体轻钢龙骨骨架、泡沫混凝土、外侧面板、简化砂袋、螺栓连接件共同组成。

其中龙骨材料采用的冷弯薄壁型钢，本构模型采用准静态拉伸得到的Q235钢在常温下应力应变曲线来表征相对合理[16]，材料密度为7.85×10-6kg /mm3，线膨胀系数为1.2×10-5，弹性模量为2.06×105MPa，泊松比为0.3。为反应实际情况，对轻钢龙骨做开孔与切割处理并装配组成为整体骨架形式，轻钢模型如图4所示。

图4 轻钢龙骨整体骨架模型

泡沫混凝土采用王博群[17]提出的修正后泡沫混凝土本构关系，采取ABAQUS混凝土塑性损伤模型来考虑其塑性发展，参照由苏步云[18]研究所得的泡沫混凝土塑性损伤本构曲线可以较好模拟本文研究的混凝土受到各种动态作用力下的动力学行为，混凝土塑性损伤模型参数取值如下：膨胀角30°，偏心率0.1，K为0.666 7，fbo/fco为1.16，粘性系数0.005。

5.2 单元类型与网格划分

轻钢龙骨由于腹板厚度较薄选择四节点线性减缩积分三维实体壳单元进行模拟较为合适，采用种子散点布置自由网格划分；混凝土与面板选择显式八节点线性减缩积分单元，采用规整结构网格划分；六面体单元不适合简化砂球与螺栓连接件，宜采取四面体单元进行自由网格划分。

5.3 碰撞接触与边界条件模拟

通过ABAQUS中的约束操作将整体轻钢骨架采用Embeded region约束类型嵌入到泡沫混凝土层内部。外侧面板与泡沫混凝土层采取Tie接触。复合墙体上下侧通过Load设置固定约束模拟室内复合墙体的实际情况，边界固定如图5所示。

图5 模型边界条件

砂球采用Rigid body绑定于球心基点，通过对基点施加平动速度场模拟冲击过程，砂球与墙体接触面设有Surface to surface contact接触形式，接触碰撞模型如图6所示。

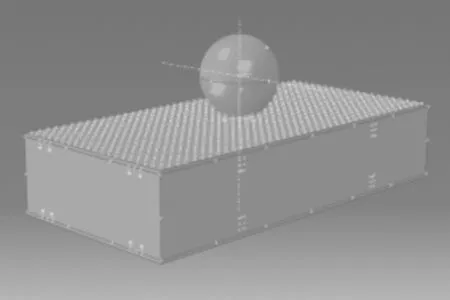
图6 接触碰撞模型

5.4 ABAQUS碰撞模型应力云图分析

通过数值模拟得到复合墙体受到低速物体碰撞后墙体应力云图变化如图7所示。

由云图得知复合墙体受碰撞接触面会发生小变形并产生均匀的应力变化，冲击力值的变化以圆波纹形状从面板中心向四周展开并逐渐衰减，如侧剖面应力云图7(a)所示；碰撞在面板上的力传递给泡沫混凝土层，复合墙体内部的轻钢整体骨架受到泡沫混凝土层的挤压发生变形，观察可知两侧竖龙骨中间区域产生较大应力变化，如图7(b)所示。

(a)

5.5 有限元模拟结果与理论计算结果对比验证

将ABAQUS有限元模拟结果同理论计算结果进行对比，如表3所示。

表3 模拟结果与理论计算结果对比Table 3 Comparison of simulation results and theoretical calculation results碰撞接触时的速度/(m·s-1)有限元数值结果 / kN理论计算结果/kN有限元与理论结果对比率4.438.197.311.125.4210.198.981.13

由表3可知数值模拟值大于理论计算的算法值，分析是因为计算碰撞过程中有惯性力以及摩擦损耗影响，但数值模拟时没有考虑，导致计算时的冲击能量相较有限元分析值偏小。总体而言理论计算与数值模拟结果的误差小于15%，证实本文模型是有效准确的，验证了理论计算算法的有效性。

6 结论

本文以复合墙体为主要研究对象进行拓展理论分析，得到适用于复合墙体的冲击力算法并通过有限元模拟对比分析理论计算结果，得出下面几点结论：

a.通过分析国内外冲击力计算方法和研究成果，关于物体低速碰撞隔墙墙体下冲击力计算方法目前研究较少且尚未考虑墙体整体变形影响，要得到切合实际的计算结果则不可忽略碰撞过程中的墙体整体变形与弹塑性变化过程。

b.由动能量分析法得知碰撞冲击力值随物体下落高度增大而增大，经过对比分析，基于动能量守恒分析下的冲击力大于真实值。研究表明泡沫混凝土作为一种典型的弹塑性材料，采用弹性理论计算所得冲击力值偏大，考虑材料的弹塑性质所计算出的冲击力值理应更接近实际情况。

c.以Hertz弹性和Thornton弹塑性接触理论为基础，建立墙体低速碰撞下简化计算模型，结合墙体弯曲变形机理，导出含修正参数冲击力计算方式。算法考虑碰撞面弹塑性变形特点，故计算的冲击力小于弹性碰撞理论得出的结果；冲击力与接触物体质量、速度呈正相关，接触压入深度随接触物体质量的增加而成一定比例的增大。

d.有限元模拟与理论计算结果对比验证ABAQUS数值模型的有效性与算法的准确性，分析表明未考虑摩擦损失等影响导致数值结果较大于理论计算结果，在容许误差范围内，模型能较为真实反馈实际，算法适应于复合墙体冲击力计算。本文研究为建筑隔墙墙体结构抗冲击力设防提供一定的理论参考价值。