水沙耦合模型在辽宁小流域水土流失模拟的适用性分析

丰亚丽

(辽宁省盘锦水文局，辽宁 盘锦 124000)

1 引言

小流域治理设计需要对区域水土流失量进行预测，水土流失预测的精准度对于小流域治理设计的合理性十分重要[1]。早在1877年来自德国的研究学者Ew al dWollny开始进行土壤侵蚀的定量研究，直到美国研究出一个通用土壤侵蚀方程，德国研究学者的这一阶段研究才结束，这一个时期的土壤侵蚀研究主要定量研究土壤侵蚀量和一些简单因子之间的关系，这些简单的因子例如流域坡度、坡长以及植被覆盖度等，国外学者通过进行大量的实验小区进行土壤侵蚀实验并进行观测，基于大量观测数据，一些土壤侵蚀的统计模型得到了发展[2-7]。我国的研究学者在土壤侵蚀方面也同样进行了大量的研究工作，在我国早期也大都是经验统计学的方法，通过实验区域，得到土壤侵蚀的经验模型，在1953年刘善建[8]在我国首次提出一个坡面土壤侵蚀方程的公式，而后许多学者结合不同区域的地理和下垫面情况，得到了不同的土壤侵蚀经验模型，在这些土壤侵蚀的统计模型中，有代表的是江忠善[9]和刘宝元[10]两位学者分别提出的土壤侵蚀经验模型。但这些模型大都未能考虑坡面产沙量，而坡面沙量主要随水流进入河道内，需要结合水文模型对水量进行模拟，在水量模拟的基础上，实现坡面沙量的计算。为此本文建立水沙耦合模型，实现降雨侵蚀量和坡面产沙量的模拟，提高水土流失预测的精度。

2 水沙耦合模型原理

相比于传统单一考虑降雨侵蚀模型，水沙耦合模型在通过土壤侵蚀方程的基础上，增加了水文因子，计算方程为：

S=11.8×(Qsurf·qpeak·A)·K·C·P·L·R

(1)

式中：S表示为预测的水土流失量，t；Qsurf表示为场次降雨下的产流量，mm，本文结合水文模型来计算场次降雨下的产流量；qpeak表示为暴雨侵蚀力，mm，可用区域最大1 h降雨量进行表征；A表示为集水面积，km2；K表示土壤侵蚀因子；C表示为植被覆盖参数；P表示为水土保持措施参数；L表示为流域平均坡度，‰；R表示为土壤质地中的沙砾比例，%。

土壤侵蚀因子K计算方程为：

K=fs·fcl·fforgc·fsd

(2)

式中：fs表示为壤土比例，%；fcl表示为砂土比例，%；forgc表示为有机质的比例，%；fsd表示为砂砾石比例，%。

植被覆盖参数C采用如下方程进行计算：

C=exp([ln(0.8)-ln(Cmin)]·exp[-0.00115·rsdsurf]+ln(Cmin))

(3)

式中：Cmin表示为植被覆盖度的年最小值；rsdsurf表示为植被表层距离地面的高度，mm。

流域平均坡度L的计算方程为：

(4)

式中：Lhill表示为斜坡系数；ahill表示为平均坡度系数；m表示为坡比系数。

m=0.6·(1-exp[-35.835·slp])

(5)

式中：slp表示为计算区域的坡度均值，‰。

土壤沙砾比例的计算方程为：

R=exp(-0.053×rock)

(6)

式中：rock表示为砾石比例量，%。

3 模型应用

3.1 区域概况

本文以辽宁西部某小流域治理为工程实例，流域流域集水面积为24.93 km2，高程差为195 m，属于典型的大陆季风半干旱、半湿润气候，区域多年降水量均值为430 mm，径流深多年均值为60 mm，流域平均宽度为5.3 km，长度为5.6 km。流域属于中度土壤侵蚀，水蚀是流域水土流失影响的主因，侵蚀沟壑在小流域内分布较为密集，水土流失比例占总面积比例高达56.0%。

3.2 基础数据

模型输入的基础数据包括：①地形数据，本文采用的地形数据的分辨率为90 m；②土地利用/植被覆盖数据的分辨率为1 km；③土壤质地数据主要包括土壤类型、土壤质地组成；④气象数据，采用流域内气象站点的最高、最低日平均气温、太阳辐射、相对湿度、风速等数据，气象数据主要用于计算流域的蒸发，作为水文模型的输入；⑤降雨数据，采用小流域内10个降水站点数据，采用面积加权计算面平均降水量，并统计分析最大1 h平均降水量。此外考虑到水文模型的验证，本文结合小流域附近的水文站，采用面积相似方法，将水文站实测流量和泥沙数据移植到计算流域，用于模型验证。

3.3 参数设置

由于计算流域位于西部，为此本文采用超渗产流模型对水文因子进行计算，土壤侵蚀因子采用式(2)，结合设计流域的土壤质地比重进行计算得到，植被覆盖比例和水保比例这两个参数主要参考文献[11]进行设置，坡度因子结合式(4)，其中Lhill和aLill结合参考文献[12]，基于设计流域的地形数据进行确定，土壤沙砾比例主要结合土壤质地数据进行确地。超渗产流模型参数结合附近水文站水文预报方案进行确定，结果见表1。

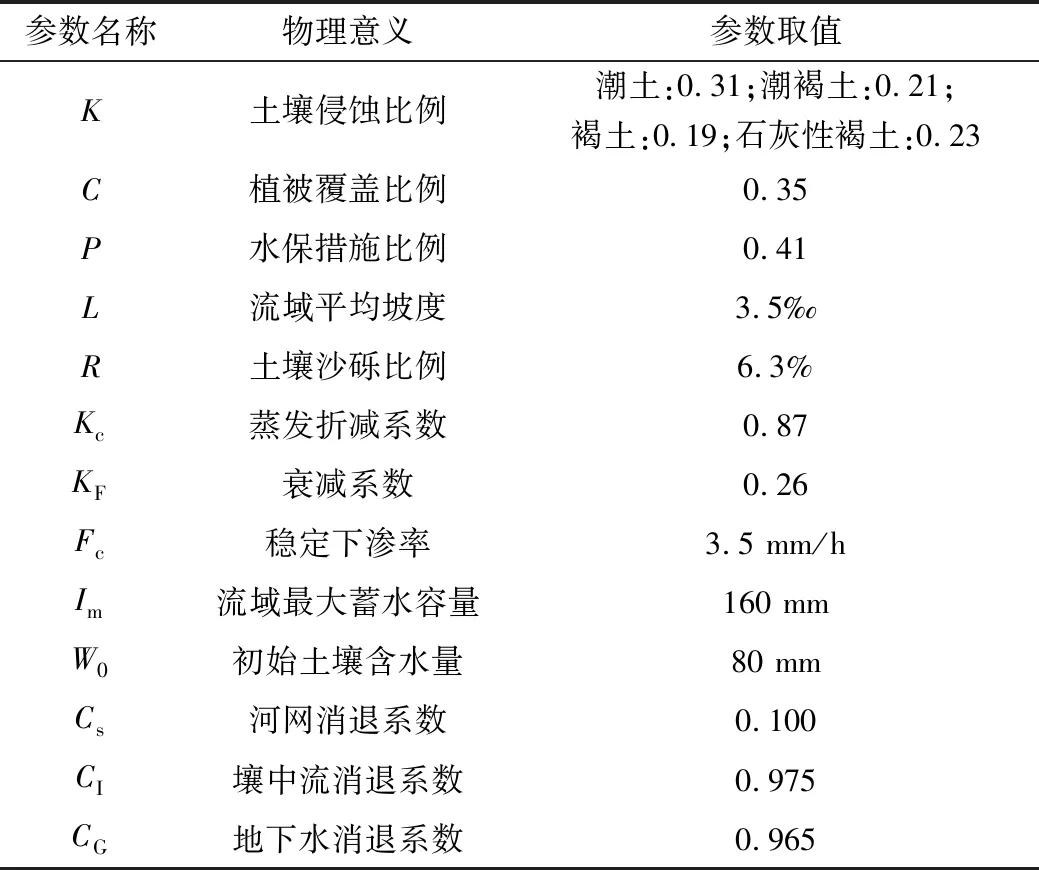
表1 水沙耦合模型参数设置结果

3.4 精度检验结果

采用对比观测试验方式，从2015年开始，进行试验小流域水土流失的观测，对场次降雨下的水土流失量进行了分析，并结合水沙耦合模型，在模型参数设定的基础上，对比分析水沙耦合模型和传统单一产沙模型(ULSE方程)的产沙量模拟精度，结果见表2，并分析典型降水条件下不同模型含沙量过程的预测精度，结果见图1。

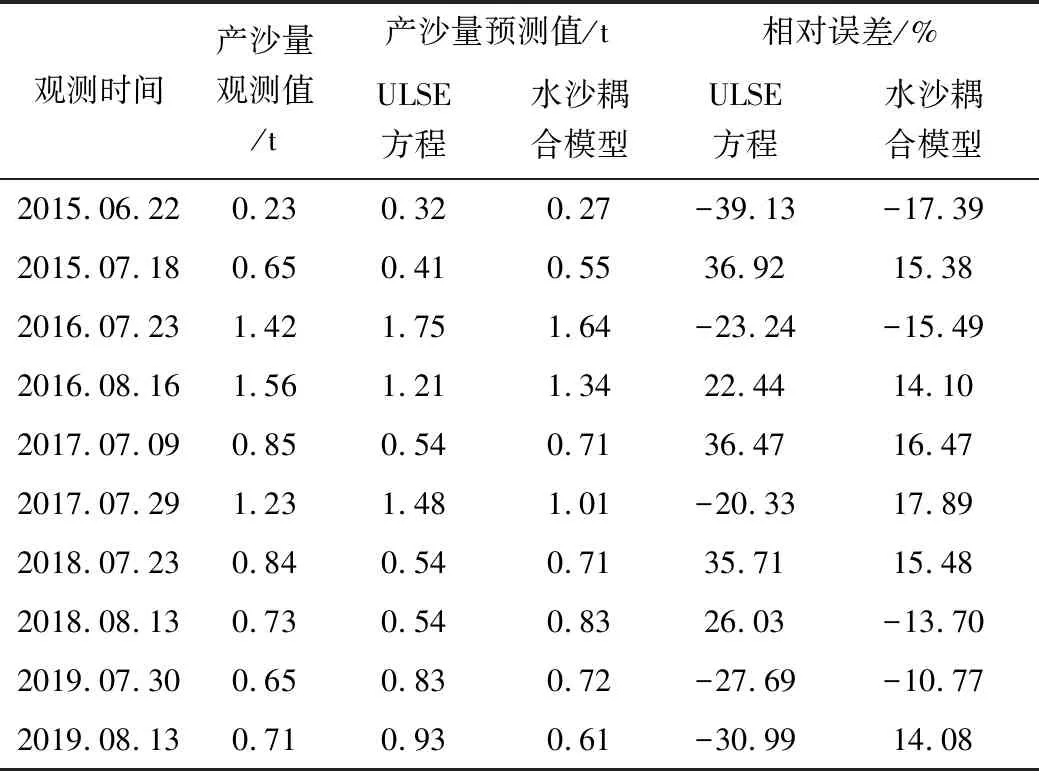
表2 产沙模型精度验证结果

从分析结果可看出，在观测的10场典型降水过程中，水沙耦合模型都较ULSE单一产沙模型的沙量模拟精度有明显改善，采用ULSE方程模拟的沙量与观测沙量的相对误差在22.44%～-39.13%之间，各场次产沙量预测的相对误差均高于20%，这主要是因为ULSE模型主要考虑降雨对土壤侵蚀的影响，预测的含沙量大部分为暴雨侵蚀量，这种模型主要适合于南方地区，当降雨的土壤侵蚀力较大时候，可以忽略坡面的产沙量。而对于北方地区而言，在暴雨条件下，由于降雨的土壤侵蚀力不高，因此坡面产沙量不能被忽略。从对比结果可看出，采用水沙耦合模型后，对其地表径流进行模拟，综合考虑降水产沙和坡面径流产沙，6场降水过程下，水沙耦合模型预测的沙量和观测沙量的相对误差在-10.77%～17.89%之间，均低于20%，相比于单一考虑降雨的ULSE模型，预测的精度平均提升14.8%。从图1中可看出，水沙耦合模型的含沙量过程预测值和观测的逐时段含沙量值均有较好的吻合度，ULSE方程虽然在沙峰过程模拟较好，但是总体的吻合度要低于水沙耦合模型。综上，可见水沙耦合模型由于综合考虑降雨和坡面汇流对产沙的影响，产沙量预测精度得到较好的提升。

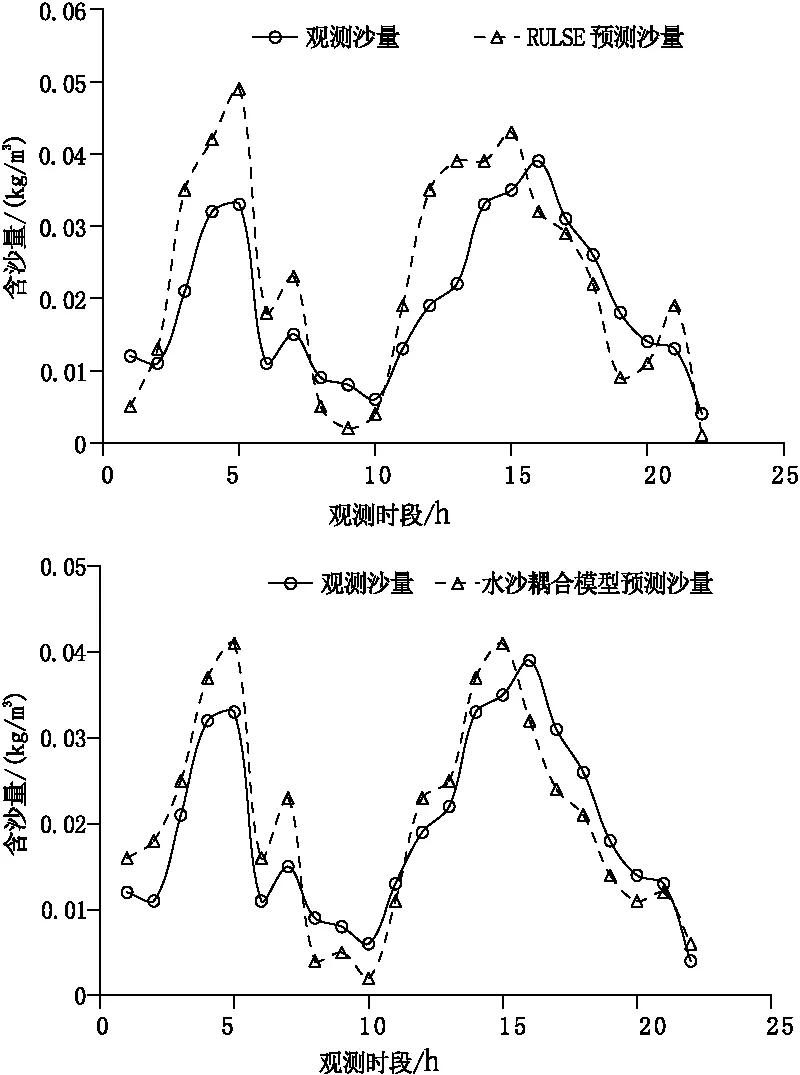
图1 各模型含沙量预测过程对比

3.5 土地利用变化下的产沙量响应分析

土地利用变化是小流域治理关键措施之一，结合水沙耦合模型，通过对应的土地利用数据，调整植被覆盖度因子和水保措施参数，即可对不同土地利用方式下沙量进行预测，为此本文通过设定3种土地利用变化情景，并对各情景下的产沙量进行预测，结果见表3。

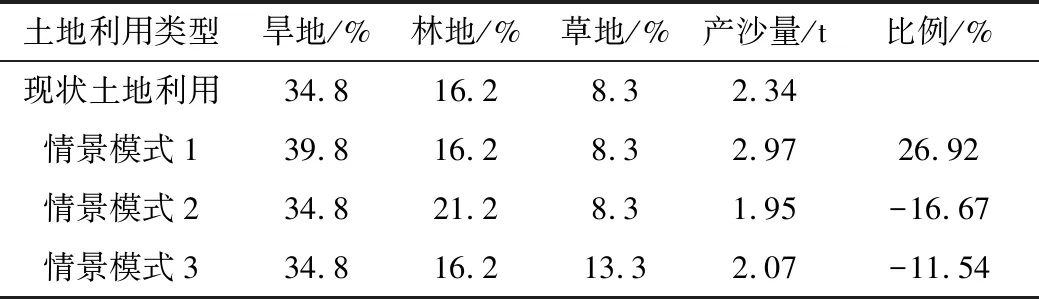
表3 不用土地利用情景模式

从土地利用情景模式变化情况可看出，情景模式1相比于现状土地利用增加了旱地的面积，增加比重为5%，其他土地利用比重不变，从情景模式1的产沙量预测结果可看出， 旱地面积的增加，使得产沙量增加幅度为26.92%，产沙量递增较为明显。而情景模式2下主要是增加了林地的面积比例，其他土地利用方式不发生变化，从情景模式2下的产沙量预测结果可看出，相比于土地利用未发生变化前，产沙递减幅度为16.67%，可见增加林地面积后，流域产沙量削减效果较为明显。土地利用情景模式3主要是增加了草地的覆盖面积，对应的产沙量削减幅度为11.54%，少于林地增加的情景模式下的产沙量削减比例，从而可以看出，草地面积的变化对流域土壤侵蚀能力改善程度低于林地面积的变化。

4 结语

(1)水沙耦合模型可综合考虑暴雨对土壤侵蚀的影响及坡面产沙的影响，在小流域水土预测的精度明显高于传统单一考虑降雨侵蚀下的沙量预测精度，适合于北方小流域水土流失预测；

(2)通过预测分析，对于水沙耦合模型而言，水量模拟的精度也将直接影响沙量的模拟精度，因此在运移水沙模型进行预测时，要结合小流域的水文特征，选定不同水文模型进行产沙量的预测；

(3)林地对于小流域产沙量削减幅度效果较为明显，其次为草地，增加相同比重的旱地，其产沙量的增幅远高于同比例林地或草地下的沙量削减比例。