基于数据包络分析法的灌区相对有效性评价

吴浩力，吴方力，黄 愉

(1.陕西省水利发展调查与引汉济渭工程协调中心，陕西 西安 710004；2.陕西省地下水管理中心，陕西 西安 710003)

1 引言

截止到2017年末，全国耕地面积134881.2千hm2，耕地灌溉面积68272千hm2，耕地灌溉率仅为50.6%。陕西省的耕地面积3982.9千hm2，耕地灌溉面积1274.99千hm2，耕地灌溉率32.0%，明显低于全国水平。

灌区是我国经济社会发展的重大公益性基础设施，是维系国家粮食安全、水生态健康、水土流失和风沙治理的重要纽带，同时是城市和工业以及生态环境供水的重要载体，也是山水林田湖草系统治理和乡村振兴的重要支撑。因此，如何高效、合理的评价灌区运管水平对灌区可持续发展具有重要意义。本文主要使用数据包络分析法对陕西省值五大灌区进行评价，为现代化灌区评价提供借鉴。

2 数据包络分析法(DEA，Data Envelop ment Analysis)

数据包络分析法是运筹学、管理科学和数理经济学交叉研究的一个新的领域，也称“平衡基准”。其第一个模型CCR由运筹学家Charnes，Cooper等人于1978年提出[1]。该方法以凸分析、线性规划和对策论为基础，使用输入、输出数据建立非参数的经济数学模型，评价具有多个输入和输出的，拥有相同目标的运营单位或“决策单元”的相对效率。其主要特点一是不依赖过多条件假设，简化了指标间的关系分析；二是采用综合指标，不必对数据进行规范化处理，实现了无量纲化；三是不需要人为干预，由模型自动确定最佳权重，实现了客观分析；四是相关软件成熟，借助电算操作便捷。

2.1 决策单元(DMU，Decision Making Units)

任何一个生产过程或企事业单位(或部门)都涉及投入和产出两项基本活动，而从投入到产出的过程是通过一系列决策来实现的，因此，将这个生产过程或生产单位称为一个决策单元DMU(即评价对象)。通常，这些DMU应为同种类型或同属于某个领域，具有类似的投入和产出，并且，可以认为这些活动的期望都是向着资源的高效利用，实现帕累托最优状态。以灌区为例，假设对A、B、C三个灌区进行相对有效性评价，则这每个灌区就可以看作是一个DMU。

2.2 生产可能集及其公理

设每个DMU在生产活动中有m项投入，n项产出，写成向量形式分别为，；于是便可以用来表示该DMU的整个生产活动，并称集合S为该生产活动的生产可能集。它反映的是多投入和产出条件下，两者之间的技术关系(即经济学中的生产函数)。由于DEA最早是应用在基于收入和产出的经济学分析，为了合理描述生产活动的内在逻辑关系，从中引入一些公理体系，包括平凡公理、凸性公理、无效性公理、锥性公理等[2-3]。在满足上述部分公理的基础上，又引入了三个取值0或1的参数。生产可能集S的一般形式如式(1)所示：

(1)

2.3 生产前沿面与DEA有效性的判断

生产前沿面(又称包络面)是经济学中生产函数向多产出情况的推广，有关其研究始于1957年，由经济学家Machaell Farrell基于线性规划模型的生产效率测度思想所构建[4]。国内魏权龄、王金祥等人[5-6]对该理论有过系统深入的论述。简而言之，生产前沿面指从DMU中观测输入和输出数据包络面的有效部分，可以理解为帕累托最优点构成的面。而DEA方法的本质就是判断DMU是否位于生产可能集的前沿面上。

落在前沿面上的DMU被认为具有相对有效性，称“DEA有效”。确切的说应是“DEA弱有效”，因为DEA有效还需要满足两项权重系数u、v大于0的条件。相关数学表达如式(2)所示，其中hjo表示模型的相对效率值，简称效率指数，其经济学含义为相对生产率，根据相关性质[7]，其与量纲选取无关，其值等于1即表示DMU位于生产前沿面上，此时即为DEA弱有效。相反的，没有在前沿面上的DMU是相对无效率的，其值介于0～1之间；u、v表示权重系数，其并非由主观的价值取向得出，而是由模型本身求得的最优权重，这就较好的排除了主观因素的影响，pj、qj分别表示投入和产出。

(2)

2.4 技术有效、规模收益和综合技术效率

技术有效又称纯技术效率，反映的是DMU在最优规模时投入要素的生产效率，可通过产出/投入的比值来测度，通常受技术和管理等因素制约。规模效率反映的是实际规模与最优生产规模的差距，主要受规模因素影响。综合技术效率是对DMU的资源配置能力、资源使用效率等多方面能力的综合衡量与评价。通常认为，综合技术效率=技术有效×规模效率。综合技术效率=1，表示该决策单元的投入产出是综合有效的，即同时技术有效和规模有效，当采用CCR模型时，就认为DMU同时为技术有效和规模有效。纯技术效率=1，表示在目前的技术水平上，其投入资源的使用是有效率的，未能达到综合有效的根本原因在于其规模无效，因此，其改革的重点在于如何更好地发挥其规模效益。

2.5 DEA方法原理及其经典模型

DEA方法核心思想是使生产率越大越好。经典的模型方法是基于DMU的投入、产出构造生产函数和不失一般性的约束条件(为分式规划)，利用分式规划CC-变换[8]将模型中生产函数转化为的线性规划的目标函数，同相关约束条件一起合称为原线性规划(PCCR)，为了降低运算量，再利用线性规划理论对其进行变换，将其转化为对偶线性规划(DCCR)，易知对偶规划与原规划是等价的，再求DCCR最优解的过程。由于生产活动一般都伴随着多项投入和产出，按照模型的要求，需要将这些投入和产出合成单一的投入和产出，而这种合成，就需要借助权重向量，这里权重向量正好揭示出DMU的重要性排序。利用约束条件求解线性规划的最优解即是计算权重向量。方法流程图见图1。

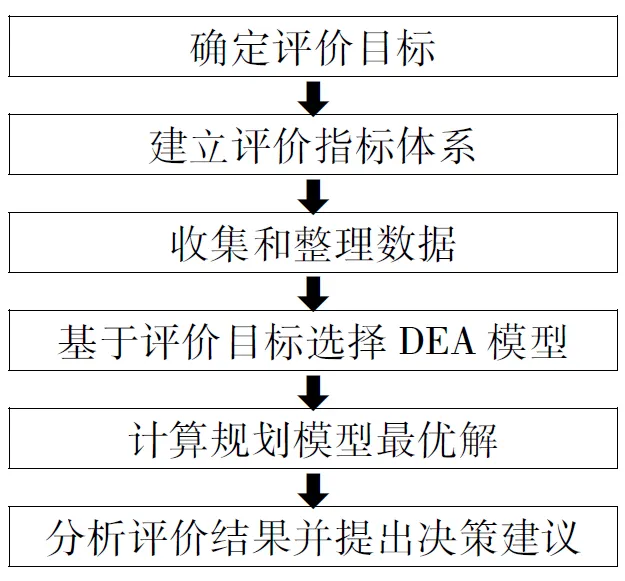
图1 DEA方法流程图

DEA方法自诞生以来，受到众多学者的追捧，并针对不同类型的决策单元开发了大量模型，如CCR模型、BCC模型和交叉效率模型等。其中，最早同时也是普适度最高的当属CCR模型，包括经典CCR模型和含非Archimedes无穷小量的CCR模型。非Archimedes无穷小量是一个小于任何正数且大于零的数，在实际应用中通常量级为1×10-5，过大有可能造成目标函数无边界，过小则可能使对偶模型无解[9]。有关其引入模型的合理性仍存在争议，相关文献可参考[10]。

ε→0 Λε>0

CCR模型假定DMU的规模收益是不变的，也即是说投入量和产出量是成正比例关系，本文既采用该模型。其以投入为导向的分式规划模型如(3)所示：

(3)

式中：vT、uT分别表示DMU输入和输出的权重系数向量；I表示为投入导向模型。

CCR的原线性规划模型PCRR见式(4)：

(4)

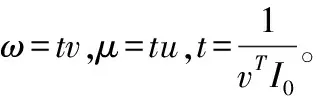
CCR的对偶线性规划模型DCRR见式(5)：

(5)

式中：θ、λ为DCRR的最优解。θ表示DMU距离包络面的径向距离；λj可将各个有效点连起来形成包络面。

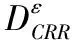
(6)

式中：s+、s-分别为松弛变量与剩余变量，其作用是使包络面沿着水平和垂直方向延伸。

2.6 陕西省直属五大灌区基本情况

陕西省直属灌区有宝鸡峡引渭、泾惠渠、交口抽渭、石头河水库和桃曲坡水库五大灌区，均为公益二类事业单位。五大灌区总设计灌溉面积429.06千hm2，总有效灌溉面积377.56千hm2，占全省灌区总有效灌溉面积的42.9%，总实际灌溉面积286.45千hm2，占自身有效灌溉面积的75.87%，累计节水灌溉面积205.09千hm2，占全省节水灌溉面积21.24%。涉及总灌溉人口492.01万人，分别占全省总人口和关中地区总人口的12.69%和20.27%。详细情况见图2、图3。

图2 省直五大灌区灌溉面积情况

图3 全省灌区有效灌溉面积占比情况

2.7 评价指标的选取

大型灌区的综合运行状况评价是一项复杂的系统工程，涉及项目目标评价、设施状况和管理水平评价、项目效果和效益评价、资源及环境可持续性评价、社会评价等诸多方面。因此，需要大量的指标和数据的支撑，这些数据来源于不同的利益相关者，搜集难度较大，加之有些数据不全面、口径不一致或更新不及时，不能客观的反映评价对象的真实状况。

本文经过对省直五大灌区的现有数据资料的分析，指标体系整理结果见表1，共计28项。在此基础上清除无效数据，见表2。

表1 灌区综合评价指标体系

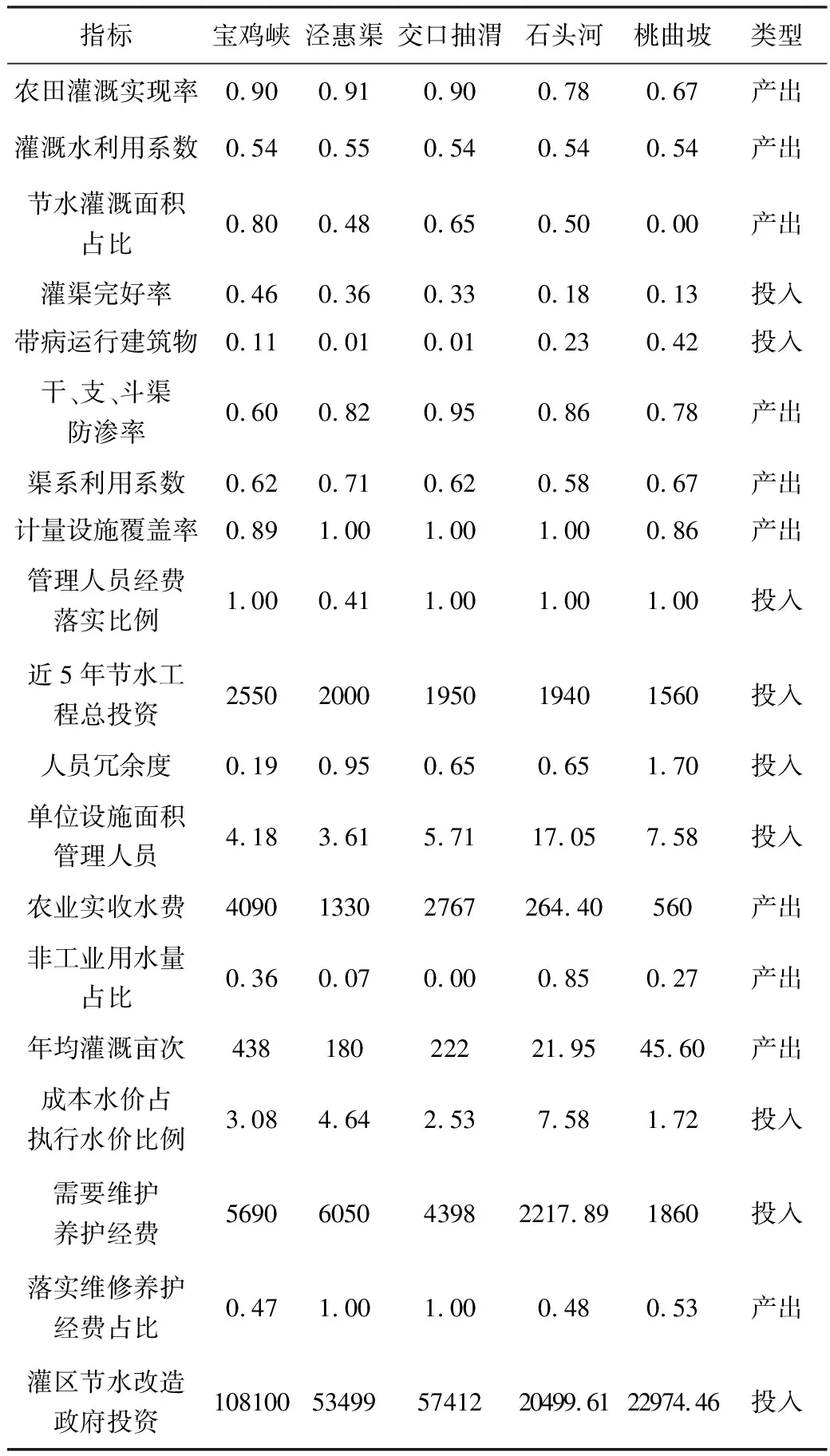
表2 指标数据

2.8 计算分析评价结果

Cooper[11]认为，DMU数量应满足式(7)的要求，而本例中只有5个DMU，故最多只应有一项投入指标和一项产出指标，但若只选2项指标结果会以偏概全，使评价结果置信度低，为此，本文借助主成分分析法，使上述指标在降维的同时又保证了信息丢失最小化。降维后的投入和产出见表3、图4。对于单投入和单产出的DEA模型则可以直接用产出比投入来表示：

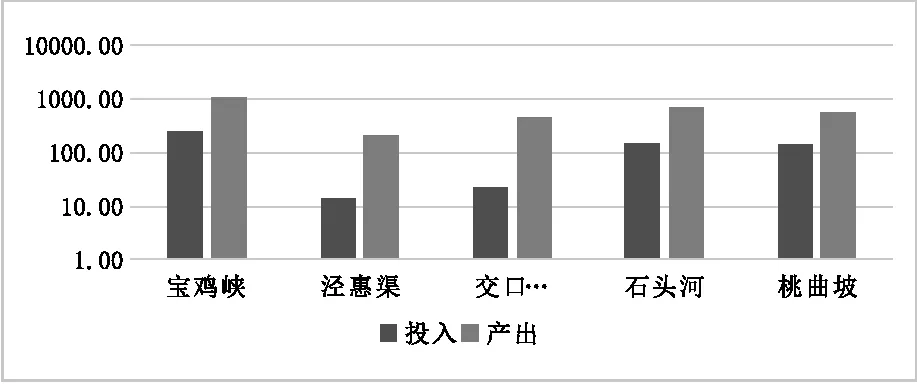
图4 五大灌区投入产出对数图

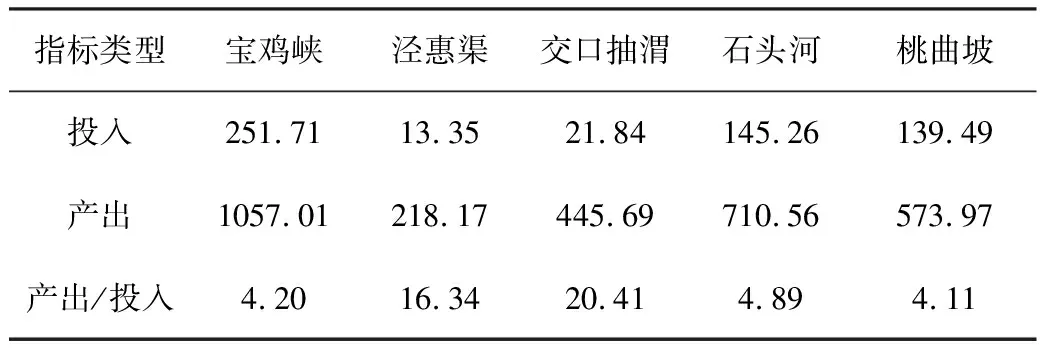
表3 降维后指标

t≥max{m×n,(m+n)×3}

(7)

式中：t为DMU的个数，m、n分别为投入和产出指标的个数。

通过上述分析，可知目前交口抽渭的相对有效性最高，也即是说，在相同的生产条件下，其产出率最高，后面依次为泾惠渠、石头河、宝鸡峡和桃曲坡，作为五大灌区之首的宝鸡峡，其规模最大，但其产出与其投入并不匹配，五大灌区产出投入比平均水平为9.99，宝鸡峡为4.2，占平均水平的42%，和交口、泾惠渠还有一定差距，需要加强设施维护和提高管理水平；石头河和桃曲坡排名靠后是由于其主要给城市供水，农业供水相对薄弱，同时存在水资源短缺和灌区节水措施有待改进的问题。

3 结语

由于本文的分析主要是侧重于农水方向，同时也缺乏必要的数据，如综合经营情况、制度管理等，所以排名只反映灌区在支撑农业方面的相对有效性。如石头河虽然排名靠后，主要是石头河主要是向城市供水，农灌较少的缘故。要全面公允的评价五大灌区的综合运行情况还需更多详实数据资料，但这不影响DEA方法评价的有效性；再者，实例中的评价单元只有5个，对于DEA方法而言，往往评价单元越多，所构建的前沿面就越精细，计算结果置信度就越高；此外，最后，DEA方法还有很多种模型，本文只抛砖引玉采用CCR模型予以评价，某些过程和假设或与现实情况有出入，值得进一步探索挖掘。