考虑气体压力时的隧道围岩渗流场分析

郭 菁，彭杰帅，白 薇，罗 超，唐 祚

（湖南南方水利水电勘测设计院有限公司，湖南 长沙 410007）

1 绪 论

1.1 研究背景

随着我国城市化建设的发展, 基础工程建设的规模和工程难度越来越大, 工程事故时有发生, 大量的地下工程事故均是由地下水造成的, 其主要原因是隧道开挖后地下渗流场的改变所引起的隧道周围应力场的改变[1]，故而引起隧道围岩的变形或者失稳。因此，在存在地下水的不良岩土体中开挖隧道时，需要解决地下水的问题。一般情况下，地下水的处理对策主要分为两大类，即堵水和排水[2～5]。“堵水”主要就是通过灌浆等方法来改善岩土体的渗透系数，以此来达到止水的目的，混凝土作为一种胶凝材料，其本质就是一种化学凝结剂[6]，对于环境有一定的影响；而“排水”主要就是通过排水的方法使地下水位低于工作面，当地下水位线大量下降时，一方面会扰动附近地下水的运动状态[7]，另一方面，由于大量抽取地下水，引起地下水位线下降，造成河流、泉水枯竭，破坏城市景观，同时还会引起较大面积的地面沉降[8]，危机已有建筑物的安全。

压缩空气作为水下隧道及软土沉箱作业的一种廉价支护及止水手段，已经有150 多年的历史。在欧美、中东及澳大利亚等地区，许多主要的隧道及沉箱工程作业中都使用了压气技术[9～10]。根据文字记录，英国于1851 年最早使用压气隧道施工技术[11]。

1.2 研究内容和研究方法

1.2.1 研究内容

在对渗流的分析研究上，本文研究了在考虑隧道中气体压力的影响时，隧道周围渗流场的变化，具体内容如下：

1）介绍了水气两相非饱和渗流基本理论，介绍了非饱和渗流的控制方程，给出了渗流方程的定解条件。

2）运用GEO-STUDIO 系列软件，建立渗流场分析模型，对隧道周围的孔隙水压力分布的变化规律进行模拟分析。

1.2.2 研究方法

GEO-STUDIO 系列软件中，AIR/W 模块是一款内置SEEP/W 模块中的用于水-气两相流分析有限元软件，适用于岩石和土等多孔介质材料中地下水与空气的相互作用分析。AIR/W 模块与SEEP/W 模块通过基质吸力耦合，气压的变化会导致水压的变化，反之亦然，既可以被应用于饱和稳态问题的求解，也可以被应用于饱和-非饱和时变问题的分析。本文的研究路线如图1 所示。

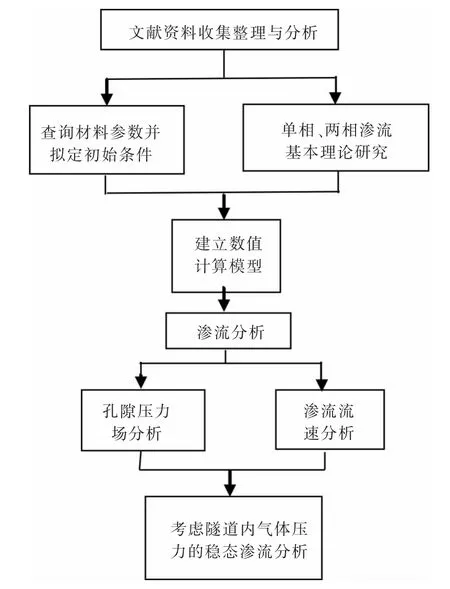
图1 研究技术路线

2 两相渗流基本理论

达西定律的表达式为：

或：

式中 q——流量（m3/s）；

k——渗透系数（m/s）；

A——渗流截面面积（m2）；

i——水力梯度；

ν——达西速率（m/s）。

达西定律最早在饱和土中得到和应用，后来经过试验证实也同样适用于非饱和土中，只是在非饱和土中应用时，渗透系数不再是定值，它将成为是一个变量，随土体饱和度变化而改变。

式（3）即为二维渗流的质量守恒方程微分形式：

式中 H——总水头（m）；

kx、ky——x 和y 向的渗透率（m2）；

Q——边界流量（m3/s）；

θ——体积含水量；

t——时间（s）。

在稳态渗流条件下，在一个单元中，流入和流出的量相等，此时方程右侧求导后为零，即：

体积含水量的变化取决于应力状态的变化以及土壤特性，对于饱和状态以及非饱和状态而言，这种应力状态可以用σ-ua和ua-uw来刻画，其中：σ 为总应力；ua为孔隙气压力；uw为孔隙水压力。假定岩体总应力以及孔隙气压力不变，这就意味着σ-ua对岩体的体积含水率没有影响，孔隙水压力的变化关系可用下式表示：

式中 mw——土壤水分曲线的斜率。

（2）破胶剂投加量确定。取3号样品加入不同浓度AP破胶剂，考察破胶后脱水率、COD去除率、色度，试验结果见表3。通过数据分析可以看出，随着AP破胶剂加量的增加，整个破胶效果变好，当破胶剂加量达到2.0%时，破胶后各项指标均达到较好的效果，再增加破胶剂投加量，破胶效果变化不大，因此，选择破胶剂加量为2.0%。

总水头H 可表示为：

式中 uw——孔隙水压力（Pa）；

γw——水的重度（N/m3）；

y——高度（m）。

结合式（5）和式（6）可得：

由式（7）和式（3）可得：

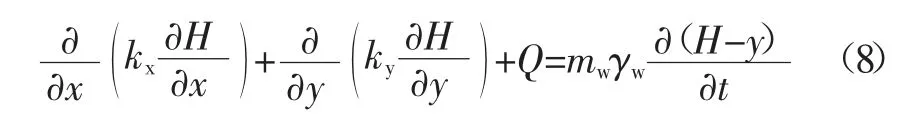
与单相流的连续方程表达式类似，对于气水两相不混溶渗流，气水两相流的连续性方程可表述为：

式中 下标a 和w——表示气相和水相；

φ——孔隙度；

s——饱和度；

▽——梯度算子；

V——体积；

q——流量。

多孔连续介质气液两相流的控制方程为：

式中 κij——本质渗透率张量；

kra和krw——气体和水的相对渗透系数；

pa和pw——气体和水的压力；

pc——毛细压力；

Sw——水饱和度；

φ——孔隙介质的孔隙率；

βa——气体体积升成因子；

μa和μw——气体和水的黏滞性系数；

g——重力加速度；

t——时间；

xj——笛卡尔坐标。

3 数值模型及计算方案

3.1 计算边界及初始条件

渗流计算边界：模型左、右边界概化为定水头边界；底部边界为不透水边界；顶部设为气体压力零边界；洞库设为潜在渗流面，同时施加气体压力。

渗流计算初始条件：左右边界概化为定水头边界，水头为16 m；模型底边界为不透水边界；顶部设为气体压力零边界；洞库设为潜在渗流面，并设置为气体压力边界，压力为50 kPa。

3.2 计算方案

计算方案如表1 所示。

表1 计算方案

4 结果分析

4.1 总水头

由图2 可知，在不考虑气体压力时，总水头由边界向隧道方向递减，水头最小值出现在隧道底端，最小值为4.52 m。由图3 可知，当考虑气体压力对渗流场的影响时，气体压力使各点总水头增大，水头还是由边界向隧道方向递减，在靠近隧道底部递减速度越快，在洞库下方增大值最大。

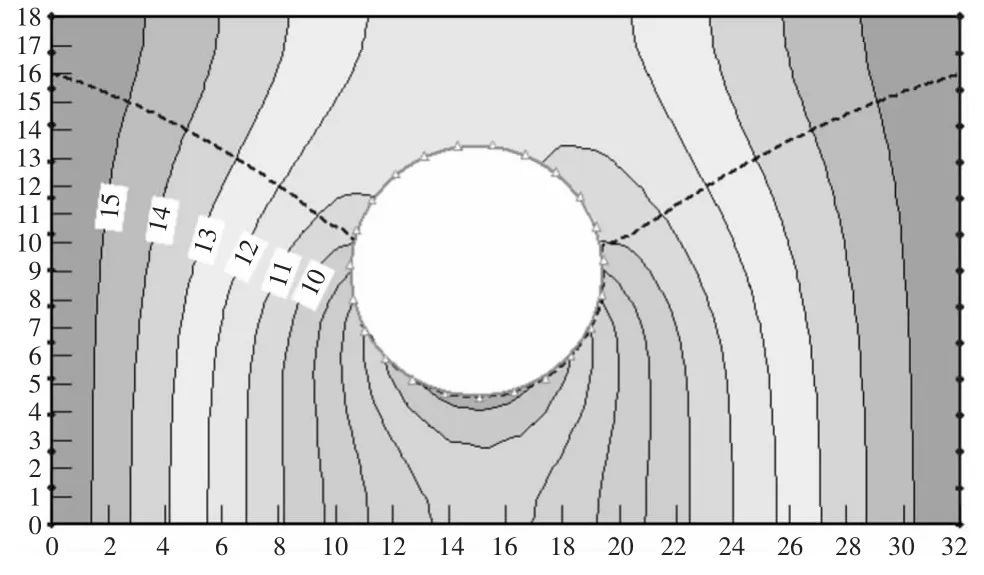
图2 不考虑气体压力时的总水头

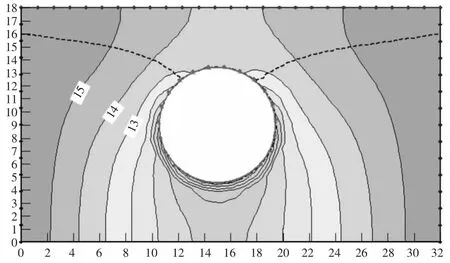
图3 考虑气体压力时的总水头

4.2 孔隙水压力

由图4 可知，不考虑气体压力时的孔隙水压力呈层状分布，压力值从上至下呈递增趋势，最小值为-65.342 kPa，最大值为156.91 kPa。由图5 可知，考虑气体压力时，由于孔隙介质全部被空气和水充满，对于每一相来讲，阻力增大，孔隙率减少，气体压力使孔隙水压力增大，浸润线抬高，隧道周围流量减半。由于在洞室的上方气压和水压的压力差最大，因此在洞室上方空气渗流速度最大。

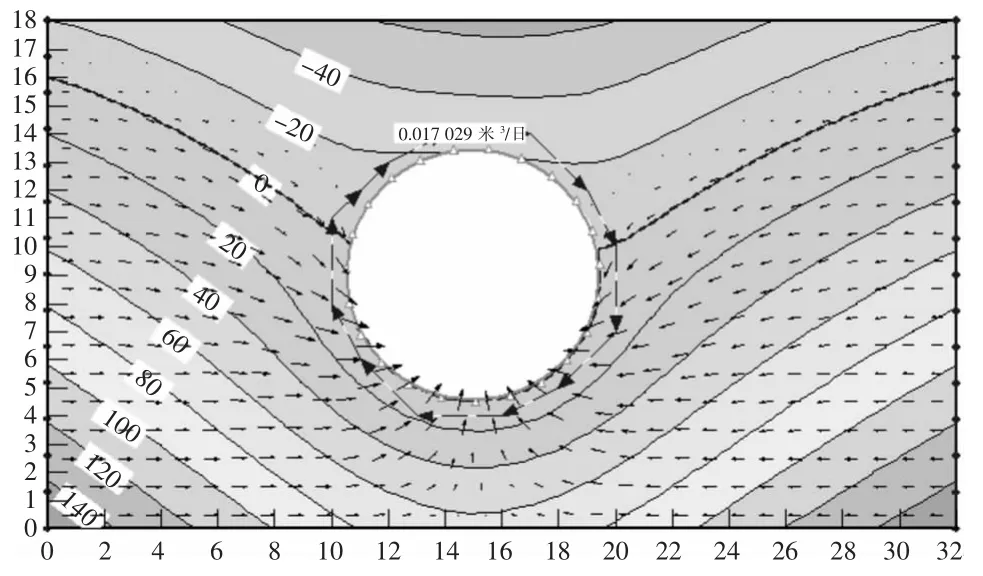
图4 不考虑气体压力时的孔隙水压力

4.3 水平流速

图5 考虑气体压力时的孔隙水压力

由图6 和图7 可知，在隧道的左下方和右下方水平流速最大，往边界方向水平流速呈递减趋势，而气体压力降低了隧道周围左下方和右下方的水平流速。

图6 不考虑气体压力时的水平流速

图7 考虑气体压力时的水平流速

4.4 垂直流速

由图8 和图9 可知，在隧道周围的左、右、下方三个方向，垂直流速较大，流速等值线密度也较大，说明在这三个位置的流速增加较快，对稳定不利。而使在隧道周围左右两个方向上，气体压力使垂直流速减少，但在隧道的底端垂直流速的增加变快。

4.5 总流速

图8 不考虑气体压力时的垂直流速

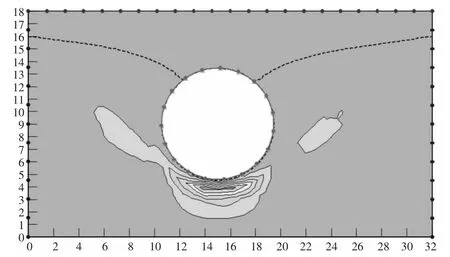
图9 考虑气体压力时的垂直流速

由图10 和图11 可知，气体压力使隧道周围流速减少，但在洞库下方流速增大且流速变化变快，对稳定不利。

图10 不考虑气体压力时的总流速

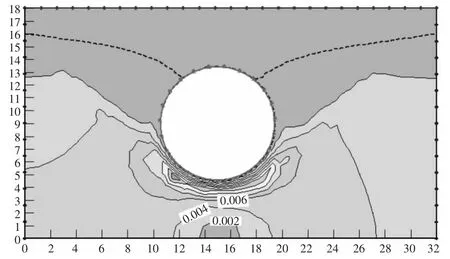
图11 考虑气体压力时的总流速

5 结论与展望

5.1 结 论

本文运用GEO-STUDIO 系列软件，建立渗流场分析模型，对隧道周围的孔隙水压力分布的变化规律进行模拟分析，得到如下结论：

1）在考虑气体压力影响的情况下，隧道周围地下水渗流会受到一定的影响，主要表现为孔隙水压力增大，浸润线抬高；隧道周围流量减半；在洞室上方空气渗流速度最大。

2）由于空气由洞内向洞外渗流，相当于对开挖面施加了一个支护力，可以从隧道中排除地下水，并减少地面沉降。

5.2 展 望

本文的分析中还存在着一些没有考虑到的影响因素，今后还要在以下几个方面进一步展开研究：

1）本文建立的是一个二维数值分析模型，为了更好地反应工程实况，建议采用三维模型。

2）在计算时隧道周围的岩体全部为粉质黏土，与实际不符。

3）在计算中采取的是孔隙介质模型，而实际上的岩层存在着复杂节理或裂隙，其渗流状态与孔隙介质存在差异。