利用主轴因子法的严重性代码异味相关性分析

张生栋，吴海涛，高建华

(上海师范大学 计算机科学与技术系，上海 200234)

1 引 言

软件开发过程中，软件维护的工作量和成本比起其它过程要大得多，而代码异味的存在使得软件的可维护性大大降低.代码异味又称代码的坏味道，是开发人员在设计代码时的不良选择,开发人员的编程习惯、经验不足或者是迫于在规定日期内完成项目的交付等原因都会引入代码异味.Martin Fowler[1]定义了22种代码异味，并详细介绍了每一种代码异味的重构步骤.近年来，代码异味的研究受到重视，检测代码异味的方法层次不穷[2-5]，并且异味的关联从不同角度被广泛研究.

Palomba[6,7]等人研究发现社区异味和代码异味之间存在着相关性，他们从社会和技术债务中使用混合方法经验收敛性评估提供两者之间存在关系的证据，并且设计了一个预测模型，使用社区异味和几个来自最新技术的已知社区相关因素来预测代码异味强度.Tufano[8]等人对测试异味和代码异味的共现进行了实证分析，实验结果表明，部分测试异味与代码异味之间存在着相关性，比如Assertion Roulette(断言轮盘赌)和Spaghetti Code(意大利面代码).Cardoso[9]和Sousa[10]都探讨了设计模式和代码异味之间的关系，并且都发现设计模式的使用不能避免代码异味的存在.

Walter和Pietrzak[11]两人使用了多标准的方法检测代码异味，其中有一条检测的标准是：是否有其他代码异味的存在.他们认为，一种代码异味的存在可能意味着相关代码异味的存在，这是由于某些代码异味的共同起源：一个代码错误会导致许多设计错误，并且所产生的代码异味并不是相互独立的.Fontana[12]等人在74个系统上对6种代码异味进行实验，深入研究了代码异味之间的共存，他们发现Brain Method(大脑方法)容易与其他代码异味共存，同时比较意外的结论是God Class和Data Class(数据类)并没有发现共存现象.Pietrzak和Walter[13]定义分析了代码异味之间的6种关系，并提出通过这些关系来减轻其他代码异味的检测工作量.Lozano和Mens[14]等人分析了3个开源系统，报告了4种代码异味中发现的5种可能关系(简单支持、相互支持、拒绝、公共重构、包含)的证据.发现Feature Envy和Long Method的相关性最强.

Abbes[15]等人首次提出了代码异味交互的概念.他们实验发现God Class(上帝类)和God Method(上帝方法)单独存在时，对系统的影响不是很大，但是当他们一同存在时，对系统质量就会造成很大的影响.Yamashita和Moonen[16]等人根据实验研究了12种代码异味的交互，并分析了这些交互和维护问题之间的关系，他们使用自动检测工具检测代码异味，并用主成分分析方法分析代码异味，以识别共存的代码异味模式.随后Yamashita[17]等人在两个开源系统和一个工业系统中对代码异味之间的交互做了实验，发现代码异味之间的交互在不同的系统上表现是不一样的.

Garg[18]等人通过位图(Bitmap)的方法分析了两个系统的7种代码异味的关联，通过百分比的形式比较了两个系统中两两代码异味共同出现的概率，他们发现每个系统都会出现代码异味共现现象，同时他们发现Data Clumps、Internal Duplication(内部重复代码)、External Duplication(外部重复代码)比较常见.

Palomba[19，20]等人在30个系统一共395个版本上，针对13种代码异味使用关联规则算法得到了6个共存的代码异味对.并且发现代码异味同时出现的现象非常普遍，59%的臭味类受多个代码异味的影响.

Walter和Fontana[21]等人采用成对相关分析、主成分分析和关联规则3种方法，对92个java系统中检测到的14种代码异味的频繁搭配进行了识别和实证验证.

本文的目标是在前人的研究基础上，针对主成分分析在布尔变量分析中会产生难以解释的主成分含义的弊端，赋予代码异味严重性，利用因子分析进行实验，与主成分分析比较，并解释每个因子的含义.

本文的主要工作如下：

1)根据代码异味检测工具检测的不一致性，对数据集进行处理，将检测到代码异味为真的工具占检测该代码异味工具的比例作为该代码异味的严重性值.

2)利用因子分析法对改进的92个系统的数据集上进行实验.

3)分析比较实验结果，并对得到的因子进行解释和分类命名.

本文的结构如下：第2章介绍了本文研究的代码异味和因子分析的相关概念；第3章研究了代码异味的严重性赋值和本文用到的方法；第4章进行实验和对实验结果进行分析及解释分类命名；第5章总结本文并指出将来的工作.

2 基本概念和术语

2.1 代码异味

代码异味是程序开发领域代码的不良设计，可能会导致深层次问题的症状.继Fowler[1]定义了22种代码异味之后，Lanza和Marinescu[22]将代码问题大致分为3类，并新定义了几种代码异味.本文研究了14种代码异味，其中有7种代码异味由Fowler[1]定义，6种由Lanza 和Marinescu[22]定义，另外1种由Trifu和Marinescu[23]定义，表1中列出了每种代码异味及其描述(后跟定义者).

表1 代码异味及其描述Table 1 Code smells and its description

2.2 因子分析(Factor Analysis,FA)

因子分析是多变量降维统计技术.它通过将紧密相关的变量归为同一个因子，以实现通过少量因子就可以尽可能表达原始数据中所有变量表达的信息的目的.

因子分析和主成分分析(Principal Components Analysis,PCA)都运用了降维的思想，因子分析的基本原理是提取对表达整个数据集信息具有最大贡献的公共因子和不属于公共因子但又不可忽略的特殊因子，然后两者线性组合表示变量.而主成分分析的基本原理是将用原始变量线性组合表示主成分，且各个主成分之间独立.因子分析是在主成分分析基础上的扩展，相对于后者，前者对于变量之间的关系的关注更为侧重.

图1给出了因子分析的流程图，进行因子分析首先需要确定所要分析的变量和样本，通过计算变量间的相关矩阵、KMO值和Bartlett′s值来检验能否进行实验,验证可以则进行因子提取，提取后的因子经过旋转后得到易于解释的因子.

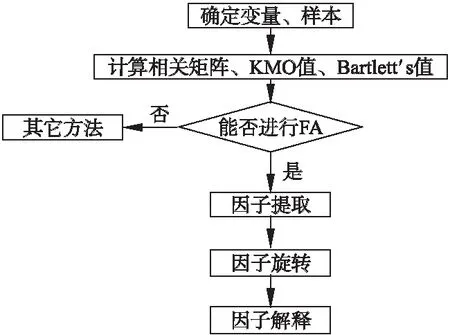
图1 因子分析流程Fig.1 Process of factor analysis

2.2.1 因子分析模型

设有m个原始变量xi(i=1,2,…,m)，它们之间可能相关，也可能独立，将xi标准化得到新变量yi，则可以建立因子分析模型如式(1)所示：

yi=ai1F1+ai2F2+…+ainFn+ciSi(i=1,2,…,m)

(1)

其中Fj(j=1,2,…,n)线性组合表示每个变量，称为公共因子，Si(i=1,2,…,m)仅与变量yi有关，称为特殊因子，aij为系数，ci(i=1,2,…,m,j=1,2,…,n)称为因子负荷，A=(aij)称为因子矩阵.

可以将式(1)表示为如式(2)所示的矩阵形式：

y=AF+CS

(2)

其中，标准化后的变量y=(y1,y2,…,ym)T,因子矩阵A=(aij)m×n,公因子F=(F1,F2,…，Fn)T,因子负荷C=diag(c1,c2,…,cm),特殊因子S=(S1,S2,…,Sm)T.

2.2.2 指标检验数据

本文采用相关矩阵、KMO值、Bartlett′s值3个指标检验数据集能否用来进行因子分析.相关矩阵也称相关系数矩阵，表示了两两变量之间的相关程度，是表示变量之间是否存在关系的最基本最常用的指标.相关系数由变量之间的标准差和协方差计算得来，通常用r来表示，其基本公式如式(3)所示：

(3)

KMO(Kaiser-Meyer-Olkin)值是本文的第二个检验指标，由于本文研究的代码异味之间关系属于多变量之间的关系，仅仅考虑简单相关系数会有很大的误差，需要同时考虑偏相关系数，KMO值便是对两者的比较.其值是0～1区间的数值，通过比较简单相关系数的平方和值和偏相关系数的平方和值来确定KMO值的大小.当前者比后者越大，KMO值越大，越趋近于1，同时也表明变量之间具有很强的相关性，反之则趋近于0，变量之间趋向于无相关性.0.5是区分有无相关性的标志，0.5～1区间内值越大越适合进行因子分析，0.5以下则不具备因子分析的条件.本文将0.5作为阈值，大于0.5表示可以进行因子分析.

Bartlett′s球度检验以变量的相关矩阵为切入点，其作用是检验数据的分布，以及各个变量间的独立情况，其显著性概率值小于0.05时才认为数据有效，可以进行因子分析.

2.2.3 公因子提取

公因子提取是在复杂的变量中提取最能够表示整个数据集信息的公因子，每个公因子充分体现了变量之间存在的相关关系.多种方法可以用来提取公因子，其中主成分分析法、极大似然法、最小二乘法、主轴因子法和Alpha因子分析法等是比较常用的方法.本文使用的是主轴因子法，该方法从相关矩阵出发，重在解释变量的相关性.

2.2.4 因子旋转

公因子提取过程中不仅提取了公因子，而且得到了每个公因子中变量的公因子方差.此时提取的公因子并不能很好地解释，需要进行旋转来使得因子矩阵更加简化，从而可以使得因子可以更直观的被解释，在因子旋转的过程中，并不会影响提取的公因子的个数.

变量正交的正交旋转和变量非正交的斜交旋转是因子旋转的两种方法，其中正交旋转有四次方最大法、最大方差法和均等变化等方法，斜交旋转有直接斜交法和最优斜交法等方法.本文采用的正交旋转的最大方差法，其主要原理是通过最大化各因子负载的平方的方差来简化矩阵.

3 基于代码异味严重性的主轴因子分析

不同代码异味检测工具的检测能力各不相同，主要是由于各个工具的检测策略以及检测规则阈值不同造成的，本文选用6种代码异味检测工具和3种方法对14种代码异味进行检测.

3.1 代码异味严重性定义

本文中的代码异味检测采用了不同的检测工具，对于同一个类，假设需要进行检测某代码异味C，设有N个检测代码异味C的工具分别记为T1,T2,…,TN，其中检测结果中检测到代码异味C存在的工具记为Tt1,Tt2,…,Ttn，个数记为n，检测不到代码异味C存在的工具记为Tf1,Tf2,…,Tfm，个数则记为m，可知N=n+m.本文定义代码异味严重性值如式(4)所示：

SV=n/N

(4)

即检测到代码异味C存在的工具个数占所有检测代码异味C的工具个数的比值.代码异味本身没有明确的定量定义，也不存在一种权威的工具明确表明某类是否存在代码异味.因此对于检测结果不一致的情况，如果一个代码异味同时被多数工具检测到，可以认为这种代码异味具有比较高的严重性，如果一个代码异味仅有个别工具检测到，可以认为该代码异味严重性并不是很高，用n/N来代表其严重性既没有忽略代码异味存在的可能性，也没有将处在阈值模糊界限上的类强行归为布尔类型上的代码异味.对于只有一种代码异味工具检测的代码异味，本文仍然按照布尔类型处理.

3.2 主轴因子分析

主轴因子法提取因子的特点是从变量的相关矩阵出发，提取的公因子能够尽可能的使得其中的变量相关，并且易于解释其中的关系和结构.而主成分分析的切入点在于变量的方差，尽量使提取到的主成分解释变量的方差，其分析过程如图2所示.

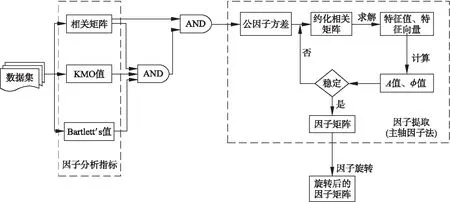
图2 主轴因子分析过程Fig.2 Process of principal axis factor analysis

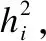
3)求出φ的估计值φ(1)=R-A1A1′；

4)返回第一步用φ(1)代替φ，直到A的值和φ的值达到稳定为止.

算法1.主轴因子法提取因子算法

输入：数据集D

输出：因子矩阵

2. forA的值和φ的值稳定

4.前q个大于0的特征值(λ1,λ2,…,λm)>0及特征向量E1,E2,…,Em←|R*-λI|=0//I为单位矩阵

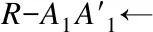
6. End for

3.3 方差最大化旋转

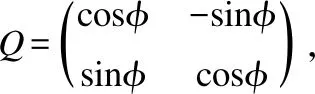
4 实 验

本节对92个系统上的代码异味进行实验，实验主要寻求解决以下几个问题：

Q1：得到的因子能否从以往的论文中找到依据？

Q2：本文采用的主轴因子法是否比主成分分析更容易解释变量的关系？

Q3：改进的数据集比原始数据有什么优势，是否更加适合进行因子分析？

4.1 实验环境

本文的实验环境如下：操作系统是Windows 10，处理器是Intel(R)Core i5-4258U CPU @ 2.4GHz，内存4GB，实验是在SPSS和PyCharm中完成，开发语言是Python.

4.2 实验数据集

本文用到的数据集是由6种代码异味自动检测工具和3种方法对92个系统中的14种代码异味进行检测得到，表2中报告了这6种工具和3种方法能够检测到的代码异味.

表2 代码异味检测工具Table 2 Code smells detecting tools

4.3 因子分析检验指标

进行因子分析的首要条件就是要保证变量之间存在相关性，以保证因子分析有意义，本文通关变量之间的相关矩阵、KMO测度和Bartlett′s球度检测进行因子分析可行性检验.

4.3.1 相关矩阵

因子分析的第一步便是计算相关矩阵，表3展示了带严重性值的代码异味的相关矩阵.

本文采用|ρ|≥0.3作为阈值，表明至少存在弱相关性(Cohen[24]，1988)，正值表明两个代码异味之间经常一同出现，负值则表明一种代码异味的存在通常排除另一种代码异味.

有8对代码异味满足设定的阈值，表中数值加粗表示.其中{Extensive Coupling、Long Parameter List}、{Long Parameter List、God Class}在原始数据集中没有出现，表中数值下划线加粗表示.{Long Parameter List、God Class}代码异味对在Walter[11]中有被实验证实；{Extensive Coupling、Long Parameter List}只在Walter[21]的实验中出现过，此代码异味对单独出现在DGDV(图表生成器/数据可视化)数据集中，被认为是一种特殊情况，而本文的实验表明这种代码异味对并非是一种特例.同时发现Extensive Coupling代码异味与Brain Class、God Class、Shotgun Surgery以及Long Method的相关值都接近于阈值0.3，说明Extensive Coupling与其他代码异味关系紧密，这也与Extensive Coupling的定义相吻合.

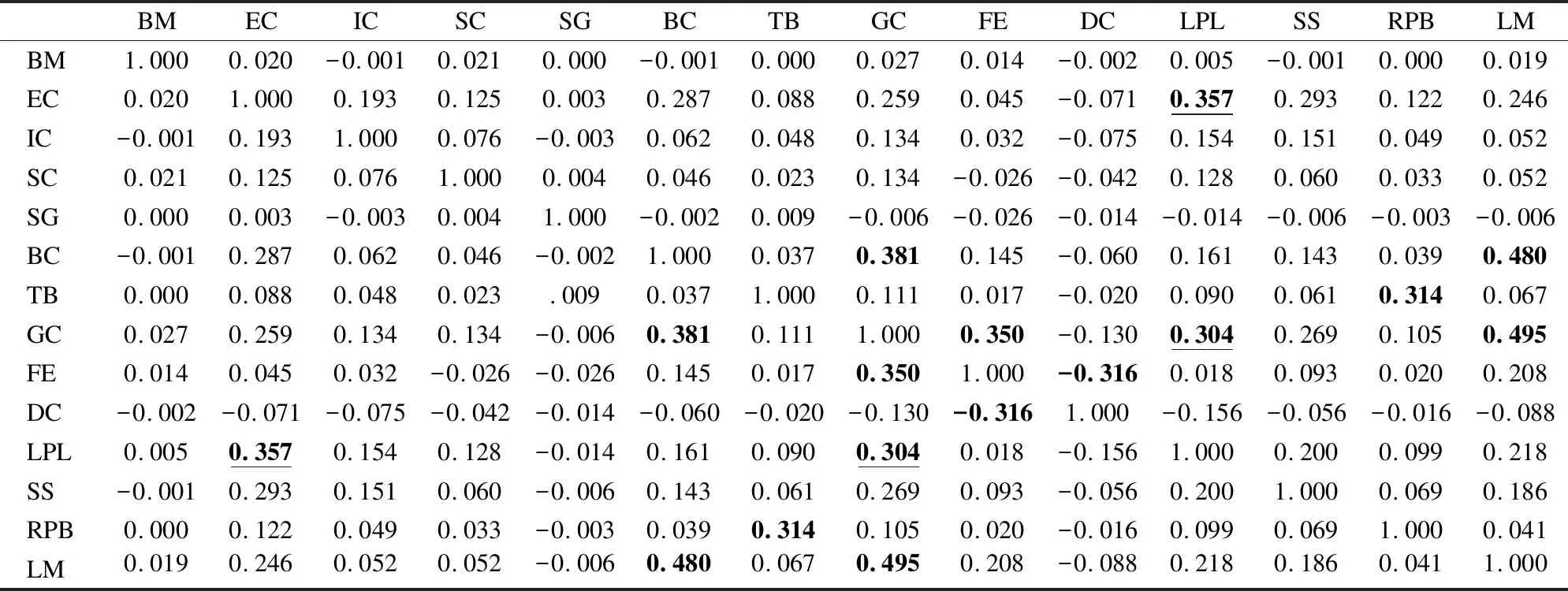
表3 相关矩阵Table 3 Correlation matrix

4.3.2 KMO测度和Bartlett′s球度检测

表4给出了KMO测度和Bartlett′s球度检测的结果，其中KMO值为0.712，高于设定的0.5的标准；Bartlett′s球度检测的显著性值为0，低于0.05的标准，二者均满足因子分析要求.

表4 KMO和Bartlett′s检验Table 4 KMO and Bartlett′s test

4.4 旋转后的因子矩阵

通过主轴因子法提取的因子矩阵需要通过旋转后才使因子更加简化和易于解释，本文采用的旋转方法是凯撒正态化最大方差法.表5是详细的旋转后的因子矩阵.

通过旋转后的因子分析矩阵可以看出有6个因子被提取出来，图3展示了提取的因子.下面对每一个因子中的代码异味进行讨论和分析.

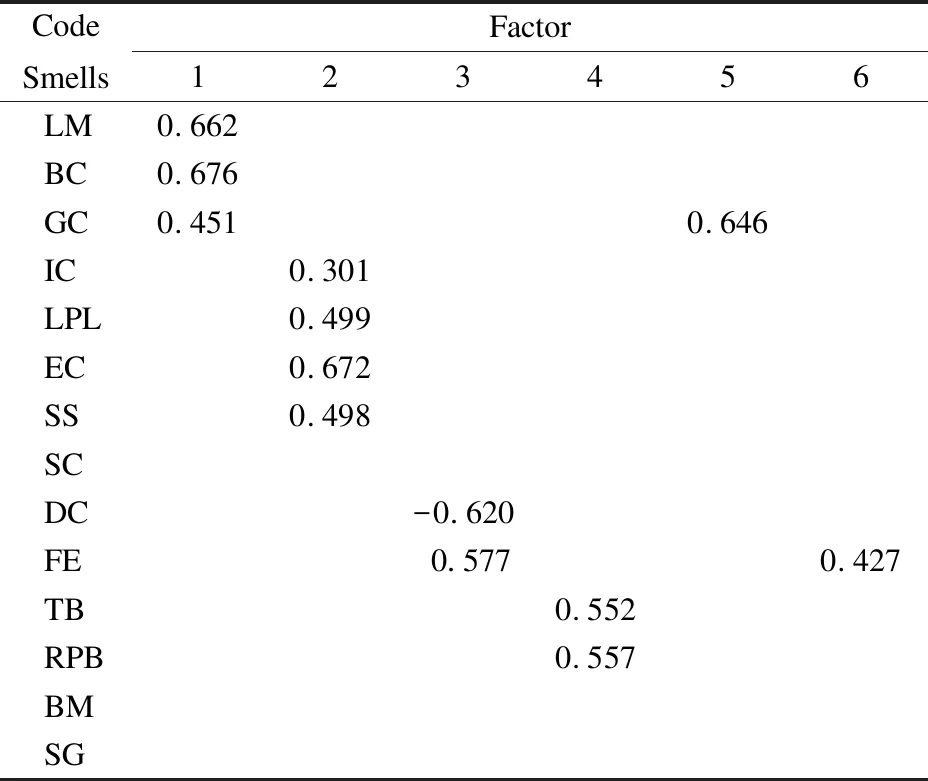
表5 旋转后的因子矩阵Table 5 Factor matrix after rotation

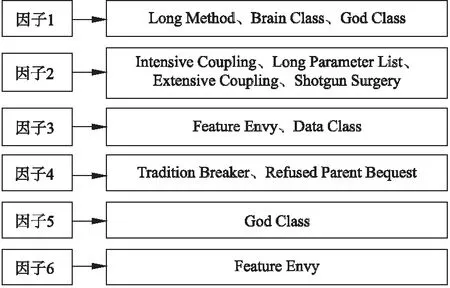
图3 提取的因子Fig.3 Extracted factors

因子1.Brain Class、Long Method和God Class被归为了因子1，Brain Class和God Class的定义很相似，都是倾向于集中系统功能的类，代码异味检测工具对他们的检测策略都是基于大小度量的，所以检测为Brain Class的类很大可能性上被检测为God Class，Brain Class和God Class中的功能太过繁杂，包含了太多的方法，Long Method也会出现于此，从定义上看该方法也是过于繁杂，需要大量的代码行、大量的变量和参数，Brain Class和 God Class更符合其存在条件，因此Long Method通常伴随着Brain Class和God Class的存在而存在.3个代码异味的共同点就是代码繁杂，囤积了太多的功能.Yamashita[17]定义这种囤积了太多功能的类为“Hoarders”，在他的分类中将Feature Envy归为“Hoarders”，通过本实验的结果和对Feature Envy的定义来看均不支持归为“Hoarders”，反而Long Method更符合要求.

因子2.Intensive Coupling、Long Parameter List、Extensive Coupling和Shotgun Surgery被归为因子2，符合在Yamashita[17]定义的第3种关系“Wide interfaces”，其描述为如果维护任务需要在显示这些异味的类中进行任何修改，则这些更改将导致由于功能耦合分散而产生的意外副作用.Extensive Coupling、Shotgun Surgery和Intensive Coupling根据定义可知3种代码异味的存在主要是由于类的耦合，至于Long ParameterList可以理解为大量参数的引入导致“被调用对象”与“较大对象”间存在依赖关系，使得Long Parameter List代码异味耦合严重，本文将这一因子不再定义为“Wide interfaces”，而是定义为“Coupling”.

因子3.Feature Envy和Data Class被归为因子3，其中Data Class显示负负荷，并不说明Data Class与此因子无关，正负与影响的大小没有关系，负号表示Data Class与此因子呈负相关.根据Feature Envy的定义，两个代码异味之间确实存在着关联，结果却比较意外，两者一般不会出现在同一个类中，标记为Feature Envy的类，一般不会再标记为Data Class，标记为Data Class的类同样也很少会被标记为Feature Envy.这种情况很符合Pietrzak[13]等人定义的“Rejection”关系.

因子4.Tradition Breaker和Refused Parent Bequest被归为因子4，从这两个代码异味的定义上看归为一个因子也在预料之中，两个代码异味都是由于子类中除了父类的方法外含有其他的方法，都属于继承体系设计错误，因此本文将这一因子命名为“Inheritance extension”.

因子5.God Class被单独归为因子5，因子1中同样存在代码异味God Class，本文认为此代码异味被单独分离出来可能是由于该代码异味出现频率很高而且会使用其他类的数据，此代码异味会与其他因子存在关联，比较明显的是因子1相关，经过斜交实验发现因子1中的God Class被去除，也证明了两个因子存在着关联.

因子6.Feature Envy被单独归为因子6，Feature Envy的存在几乎贯穿了整个数据集，根据统计，本文数据集中70%的类中存在该代码异味，有如此高的占比率，很大程度上是由于检测工具将被调用的类(Data Class除外)也标记为Feature Envy，Feature Envy更像是滴在清水里的墨水，很容易与其他类耦合在一块.

表6总结了本文得出了几种关系.同时可以先对Q1进行解答，本文得到的前4个因子都可以从过往的论文中找到依据，其中因子1、2、3的关系都有论文进行总结分类，因子4没有总结，但是因子中变量的关系明确，因子5、6则无法找到充足的依据.

表6 代码异味的关系和描述Table 6 Relationship and description of code smells

4.5 与其他方法和原始数据集的对比

本节对主成分分析提取的因子和本文用到的方法得出的结果做了对比，同时对比了在主轴因子方法下，原始数据集与带有严重性的异味数据集下的模型的好坏，并对Q2、Q3进行解答.

针对Q2：表7展示主成分分析提取的因子，可以看出，主成分分析下的前两个因子中变量都比主轴因子法得出的结果多.特别地，尽管都进行了因子旋转，但是主成分提取的因子1和因子2中都存在变量Extensive Coupling，从相关矩阵可以发现Extensive Coupling代码异味与因子1中其它3种代码异味相关系数都接近0.3，但构不成弱相关，可以视为一种极弱相关，本文的方法忽略这种极弱相关，不仅可以使不同因子中的变量尽可能独立，而且简化了因子变量，使得因子1更易于解释；对于因子2，主成分分析提取的因子2变量中多了Schizophrenic Class代码异味，结合相关矩阵，发现Schizophrenic Class与其他异味并不存在明显的相关关系，可以认为本文方法得到的结果更具有可靠性；对于主成分分析提取的因子5中的Brain Class和Schizophrenic Class并未在相关矩阵中找到两者存在相关关系的证据.综合对比表5可以看到本文用到的方法提取的因子更加简化，忽略了一些极弱相关，变量之间的关系更容易解释.主轴因子法比起主成分分析法的优势是忽略了特殊因子的影响，主成分分析得到的特殊因子各分量之间存在关联，不满足因子分析的前提条件，从而会使因子矩阵存在偏差[25].通过观察表7可以看到主成分分析得到的公因子方差并没有达到很高的水平，存在很多0.3～0.8的公因子方差值，这就说明无法忽略特殊因子的影响.同时本文的目的侧重于确定代码异味关系的内在结构，主轴因子法提取公因子正是以变量的相关矩阵为出发点确定其内在关系，而非侧重变量的方差，因此得到的结果结合相关矩阵来看比主成分法提取的结果更简化且容易解释.

针对Q3：本文从相关矩阵代码异味对、平均初始变量方差和平均KMO值3个方面对两个数据集的结果进行了比较，如表8所示.

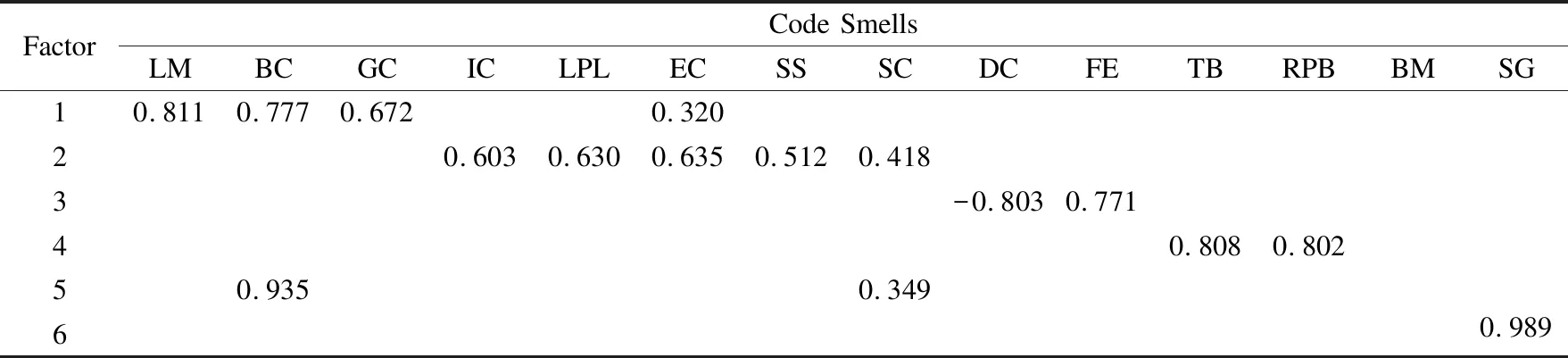
表7 主成分提取的因子矩阵Table 7 Factor matrix of principal component extraction

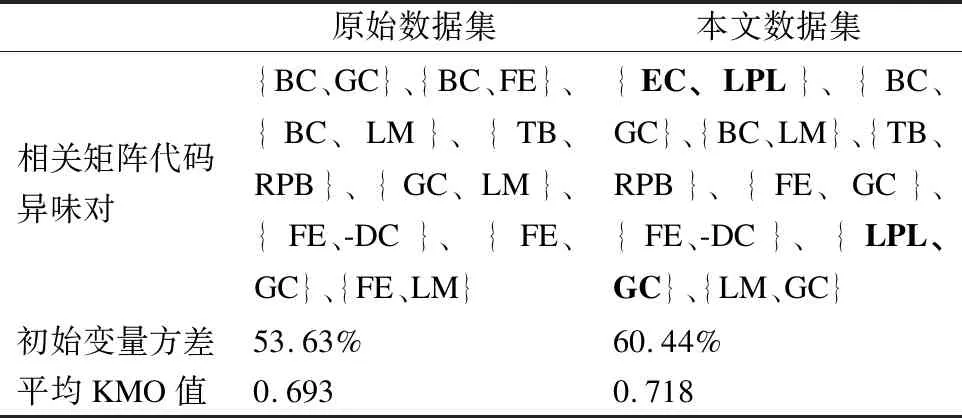
表8 数据集结果对比Table 8 Dataset results comparison

两个数据集的相关矩阵得出的代码异味对都是8对，原始数据集对于Feature Envy的关系提取的更多，主要原因是Feature Envy广泛存在于整个数据集，占比率达到了70%，没有严重性值约束下，更容易将其与其他代码异味关联.本文的数据集得出了两对代码异味{EC、LPL}和{LPL、GC}是原始数据集没有得到的，其中{EC、LPL}在之前的论文中都没有提及，唯一提及的是Walter[21]在一个特殊数据集中出现过这种异味对，但并没有进行总结.

原始有数据集的平均初始变量方差为53.63%，比本文带有严重性值的数据集的60.44%少了将近7%，之所以考虑初始变量方差而不是最终的旋转载荷方差，是因为本文用的方法出发点不在于变量方差.

对于平均KMO值，本文数据集达到了0.718，比起原始数据集的0.693也要好了很多.

5 结束语

本文对带有严重性值的代码异味进行相关性分析，将检测到代码异味的检测工具的比例作为代码异味的严重性值，然后运用因子分析中的主轴因子提取因子的方法，对代码异味进行相关性分析，从相关矩阵中得到了一种新的代码异味对，同时得到6个因子,并对其进行解释和分类，最后与主成分分析法和原始数据集的结果进行了比较，得出本文的方法可以对因子很好的解释，数据集也更加适合因子分析.本文研究的代码异味的相关性是以类为研究对象，没有考虑由于耦合类之间的代码异味的相关性，将来可以以包为研究对象，研究类之间的代码异味的关联.