Solving Nonlinear Partial Differential Equations in Mathematics with the Idea of Navier-Stokes Equation
2021-04-11HuSiyu
Hu Siyu
(Soochow University,Suzhou 215000)
Abstract:Navier-Stokes equation is the core problem in fluid mechanics.It is a momentum conservation equation describing viscous incompressible fluid.Simply put,it only describes the movement of water in the flow tube.But such a seemingly simple equation of motion,because it is a nonlinear partial differential equation,whether it has a solution or not,or even whether it is wrong at all,stumped many mathematicians and made it a century problem,so it is known as one of the seven "Millennium Prize Problems" of Clay Institute of Mathematics.The nonlinear partial differential equation in mathematics is a difficult problem in mathematics.In this paper,by analyzing two different specific cases of N-S equation as examples,we analyze how scientists have succeeded in solving mathematical problems through physical thoughts.
Key words:Fluid mechanics; Navier-Stokes equation; Nonlinear partial differential equation
1 Derivation and Introduction of Navier-Stokes Equation
1.1 Continuity equation of incompressible fluid
Firstly,rectangular micro-element control bodies with side lengths dx,dy and dz are selected in the flow field.Because the fluid is incompressible,the net fluid volume flowing out and into the microelement control bodies in dt time is zero.Let the coordinates of the center point of the control body be (x,y,z)

1.2 Differential equations of viscous fluid motion expressed by stress
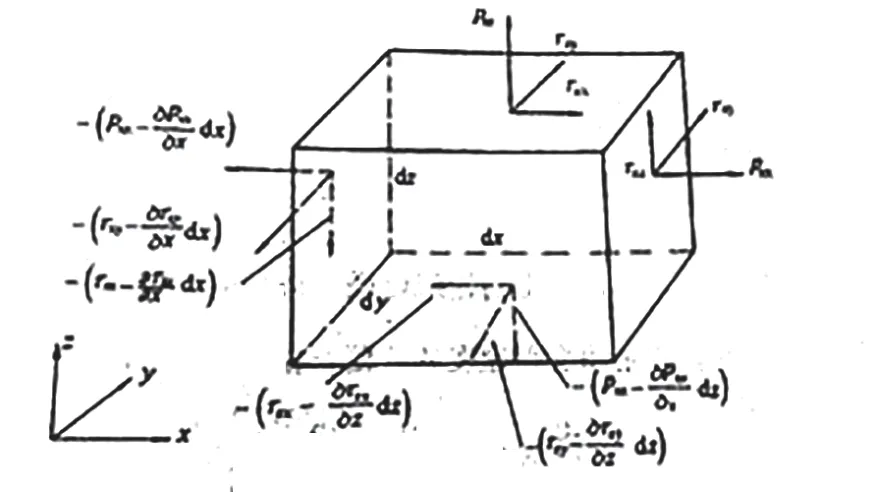
Take cuboids with side lengths dx,dy and dz as control elements in viscous fluid,as shown in the figure:
P denotes normal stress,τ denotes tangential stress,in which the first pin of stress symbol denotes the outer normal direction of the action surface,and the second pin denotes the stress projection direction.According to Newton's second law:the differential equation of motion in x direction is:

The linear deformation movement means that the normal stress decreases with the elongation deformation,so the relationship between the normal stress of viscous fluid and the linear deformation velocity is as follows:
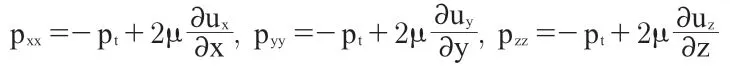

2 The Method of Solving the Exact Solution of Navier-Stokes Equation
2.1 The main purpose and thought of solving Navier-Stokes equations


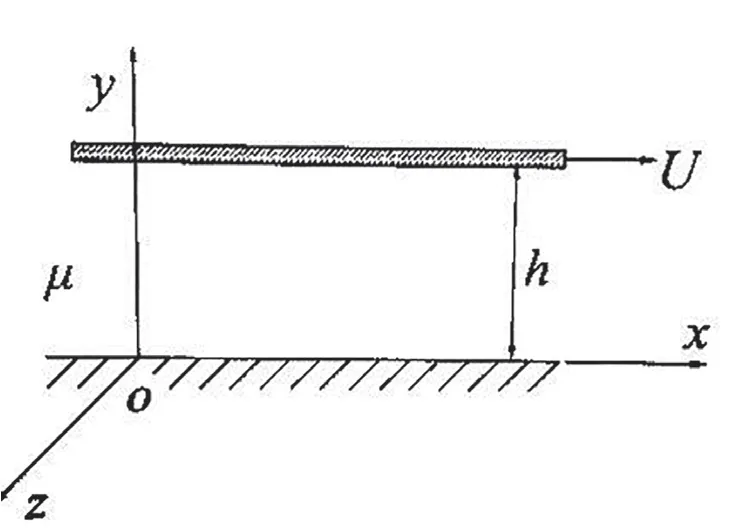
2.2 Solving Navier-Stokes equations by couete flow
It is assumed that the upper and lower plates are filled with constant fluid with viscosity μ,the distance between the two plates is h,and the upper plate moves in a straight line with uniform speed u relative to the lower plate.Due to the viscosity of the fluid,the fluid will move along with the movement of the plate,and this flow becomes Couete flow.As shown in the figure,Couete flow is parallel flow,and its speed is not 0 in only one flow direction,soAll are 0

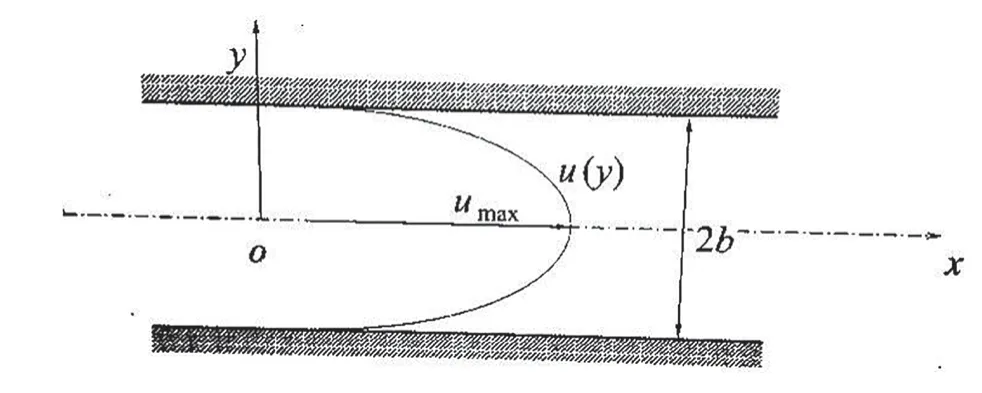
2.3 Navier-Stokes equations under Poiseuille flow
Poiseuille flow is a flow formed by the pressure gradient pushing the viscous incompressible fluid in a pipe or tank.The figure shows the Poiseuille flow in a two-dimensional channel.


3 The Efect of Physical thought on Mathemulical Poctleme
3.1 Problems encountered in mathematical research
For the N-S equation, the main question is: Does its solution exist? If it exists, how to prove it? If it does not exist, how can it be proved? For nonlinear partial differential equations like the N-S equation, from a mathematical point of view, it is very difficult for most nonlinear partial differential equations to get their general solutions with current mathematical skills. However, in practice, we need to get the solutions of this kind of nonlinear partial differential equations, so people can only settle for the next best-to solve their special solutions under different circumstances.
3.2 Physical thoughts act on mathematics
Up to now, the methods to solve this kind of nonlinear partial differential equation mainly include numerical solution and analytical solution. For numerical solution, it is closed by different model assumptions, and there are different approximate methods for different problems, such as FEM, FDM, LES and so on. The analytical solutions basically include Lars transform and Fourier transform.For nonlinear partial differential equations in practical applications,most of them are done by assuming the actual physical model and a powerful computer. Therefore, physical thought is very important forsolving nonlinear partial differential equations. For example, the N-S equation mentioned in this paper is a nonlinear partial differential equation with strong nonlinear term, so it is impossible to get its solution only by the current mathematical method. However, through the assumptions of physical models, such as Couette flow, Poiseuille flow and various turbulence models, physicists have obtained the special solution of the N-S equation, and it can be confirmed in practical experiments that the fluid flow laws predicted by the N-S equation calculated by the model assumptions are correct. Just like Professor George Keith Batchelor's thought, solving mathematical problems should be integrated with physical thinking, that is, when faced with problems that are beyond the reach of current mathematical skills, equations can be simplified through the physical characteristics of a specific situation of the problems faced, thus solving mathematical problems.
4 Conclusion
Admittedly,there is no way to find the general solution of nonlinear partial differential equations like the N-S equation,and the problems of nonlinear partial differential equations are only a drop in the ocean in mathematical problems.From this point of view,we are faced with too many problems.In the face of these unknowns,what we should do is to summon up courage,break up parts,and overcome one problem one by one step.It is of great significance for us to solve mathematical problems through physical thoughts and solve mathematical problems with specific physical models in the process of exploring nature.With such means,and with the emergence of inspiring achievements one after another,it also gives us confidence in exploring the unknown,and makes us believe that all unknowns in nature can be solved one by one[3].
