沪深两市行业板块尾部相关性研究*——基于M-Copula-t-GARCH模型

杨龙江

(河南工学院 管理学院，河南 新乡 453003)

0 引言

股票市场的相关性，因其对投资者制定投资策略及对政府部门制定金融政策等都有着重要的参考价值而日渐成为金融领域的研究热点。

目前关于股票市场的相关性研究可归为两类：第一类是关于股市收益率的相关性研究，讨论金融市场一体化带来的资产收益率的相关性变化。如崔珍等对沪深股市之间的联动性进行了研究，发现上证综合指数与深证成分指数之间存在长期的联动效应，且在危机背景下，沪深股市表现出更强的短期联动性[1]。刘光强对沪港两市之间的相关性进行了研究，发现“沪港通”实施之后两市之间的相关程度提升了12%左右，且港市对沪市的影响逐渐增强[2]。李岸等对中国股市的国际联动性进行了研究，发现随着经济全球化的加深，全球股市收益率联动性逐渐增强[3]。第二类是关于股市收益率波动性的相关性研究，讨论股市的“波动溢出”效应。李钰对亚洲具有代表性的中日韩印四个国家的股市收益率波动性进行了研究，结果表明，四个股票市场都存在波动聚集性和冲击的非对称性[4]。田海涛等对股市收益率与其波动率、股市收益率与其自相关性之间的关系进行了研究，发现波动率越高的股票月均收益率越高，且自相关性越强的股票月均收益率也越高[5]。

综上可见：(1)绝大多数文献都在研究股市整体间的相关性，很少研究股市板块间的相关性，而行业政策的发布、新技术的产生等会直接或间接地对相关板块的股价造成影响，从而影响投资者的投资策略，因此板块间的相关性是不容忽视的。(2)绝大多数文献采用Pearson相关系数来度量收益率或波动率之间的相关性，但是尾部相关系数在描述金融序列的相关关系时具有更好的特性。股市间的尾部相关性分析，不仅能帮助投资者寻找投资机会，通过恰当的投资组合获得稳健的收益，而且能帮助金融机构规避“流动性风险”，因此股市间的尾部相关性研究更应引起广泛的关注。

鉴于上述分析，本文以沪深两市为研究对象，依照中国证券监督管理委员会(CSRC)上市公司的行业分类标准，从两市19大板块中，依市值及股票份额各选取了8大板块进行研究，度量了各板块间尾部相关性并据此构建了最优投资组合策略。

1 M-Copula-t-GARCH模型

M-Copula-t-GARCH模型用以研究金融市场间的相关程度与相关模式[6]。该模型的估计与评价分两步：首先用t-GARCH模型来模拟变量的边缘分布，其次用M-copula函数来描述变量间的相关模式。

1.1 t-GARCH模型

低阶GARCH模型的效能相当于高阶ARCH模型，它使模型的识别和估计变得比较容易[7]。t分布可以很好地描述金融序列的尖峰、厚尾、偏斜等分布特性。一般情况下，t-GARCH(1，1)模型可以较好地拟合金融序列的波动情况。模型如下：

(1)

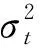
1.2 M-Copula模型

Copula函数是连接n维联合分布函数与其n个边缘分布函数的桥梁，较之传统的相关性度量方法，其具有边缘分布的选择没有限制、可将研究对象的层次结构予以明确描述等诸多优点[8]。Archimedean Copula函数族有三个主要函数，即：Gumble Copula、Clayton Copula、Frank Copula，韦艳华等人将这三个函数线性组合起来，构成一个混合Copula函数，记为M-Copula函数，模型如下：

M-Copula=wGCG+wCCC+wFCF

(2)

式中：wG、wC、wF分别为 Gumble Copula、Clayton Copula、Frank Copula函数的权重系数，wG，wC，wF≥0且wG+wC+wF=1。

1.3 M-Copula-t-GARCH模型

t-GARCH模型可以较好地拟合具有尖峰、厚尾、偏斜等分布特性及异方差、波动聚集等波动特性的高频金融数据。M-Copula模型能够更加准确、全面地描述金融序列间的相关关系。故M-Copula-t-GARCH模型有利于探索高频金融序列间的多种相关关系，适用性较强。

2 M’-Copula-t-GARCH模型

本文在分析了M-Copula模型中各Copula函数在相关性分析上的应用特点后提出了M’-Copula-t-GARCH模型，该模型更适合于描述金融变量间非对称的尾部相关关系。

2.1 M’-Copula模型的构建

由于收益率序列具有高频金融数据的分布及波动特性，所以边缘分布的拟合依旧选择t-GARCH(1，1)模型。本文旨在研究板块间的尾部相关性，下面对Archimedean Copula函数族中的三个主要函数与尾部相关性度量的关系做一简要分析。

Gumble Copula函数表达式如下：

CG(u,v;α)=exp{-[(-logu)α+(-logv)α]1/α}

(3)

式中：参数α∈[1,∞)，其密度函数呈“J”字形，上尾高，下尾低，能够捕捉到上尾相关关系的变化。

Clayton Copula函数表达式如下：

CC(u,v;θ)=(u-θ+v-θ-1)-1/θ

(4)

式中：参数θ∈(-1,∞)且θ≠0，其密度函数呈“L”字形，下尾高，上尾低，能够捕捉到下尾相关关系的变化。

Frank Copula函数表达式如下：

(5)

式中：参数λ∈R，其密度函数呈“U”字形，具有对称的尾部，无法捕捉到随机变量间非对称的尾部相关关系。

鉴于Frank Copula函数的特征，本文只将Gumble Copula与Clayton Copula函数线性组合起来，构成改进的M-Copula函数，记为M’-Copula函数，模型如下：

M′-Copula=wGCG+wCCC

(6)

式中：wG、wC分别为 Gumble Copula和Clayton Copula函数的权重系数，wG，wC≥0且wG+wC=1。

2.2 M’-Copula模型的评价

针对M’-Copula-t-GARCH模型，最优Copula函数的选取准则制定如下。

定义：设(ui，vi)(i=1，2，…，n)为取自二维总体(u，v)的样本，则样本的经验Copula函数如下：

(7)

式中：u,v∈[0,1]；I[]为示性函数，当ui≤u时，I[ui≤u]=1，否则I[ui≤u]=0；n为样本个数。

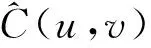
(8)

使得d2最小的Copula函数即为最优Copula函数。

3 实证研究

3.1 数据准备

3.1.1 数据获取

以沪深两市为研究对象，依照中国证券监督管理委员会(CSRC)上市公司行业分类标准，将沪深两市划分为19大板块，两市2011年1月1日至2016年6月30日各板块平均交易股票数及平均年总市值如表1所示。

表1 19大板块信息一览表

板块市值与股票数在很大程度上反映了板块的活跃性。其中板块A、B、C、D、G、I、J及K等8大板块平均年总市值之和占所有板块总和的89.7%，交易股票数分别占各市总数的81.72%和88.16%，说明这8大板块的数据具有很强的代表性，因此本文选取这8大板块进行研究。

因C板块公司数量过多，需进行随机抽样，依据经验法则，各抽取180个和125个公司作为研究样本[9]。最后从RESSET数据库中下载8大板块所有下属公司2011年1月1日至2016年6月30日的股票日数据。

3.1.2 板块收益率的计算

流通市值是由某特定时期内可交易的流通股股数乘以股价得到，选取流通市值为权重来计算板块收益率，公式如下：

(9)

为方便起见，本文以Sh_a、Sh_b、Sh_c、Sh_d、Sh_g、Sh_i、Sh_j、Sh_k分别表示沪市板块A、B、C、D、G、I、J、K的板块收益率序列；以Sz_a、Sz_b、Sz_c、Sz_d、Sz_g、Sz_i、Sz_j、Sz_k分别表示深市板块A、B、C、D、G、I、J、K的板块收益率序列。

3.2 t-GARCH模型的估计

采用t-GARCH模型拟合16大板块收益率序列的边缘分布，并对过滤后序列进行概率积分变换，检验变换后序列是否服从i.i.d(0，1)均匀分布。估计结果如表2所示。

表2 t-GARCH模型的参数估计及检验结果

h=0表示服从i.i.d(0，1)均匀分布。对变换后序列做自相关检验，发现各序列均是独立的。因此变换后各序列均服从i.i.d(0，1)均匀分布，说明用t-GARCH(1，1)模型来描述收益率序列的边缘分布是充分的。

3.3 M’-Copula模型的评价与估计

对M’-Copula模型进行参数估计前，需要对其可行性与优越性进行检验。

3.3.1 M’-Copula模型的拟合优势

分别用Gumbel Copula、Clayton Copula和M’-Copula模型来描述积分变换后新序列间的相关结构，并采用式(8)的评价标准判断模型的优越性。沪市A板块与深市A板块间的相关性检验结果如表3所示。

表3 Gumbel和Clayton以及M’-Copula的拟合优度比较

可见M’-Copula模型的d2最小，表明M’-Copula模型最具可行性与优越性。其他板块的检验结果与上表一致，限于篇幅，不再赘述。

3.3.2 M’-Copula模型的估计

尾部相关系数与Copula函数中参数的关系如表4所示。

表4 尾部相关系数与Copula函数中参数的关系

为直观表示沪深两市16大板块间的尾部相关性，分别以上尾相关系数、下尾相关系数为并类距离做聚类谱图，分别如图1、图2所示。

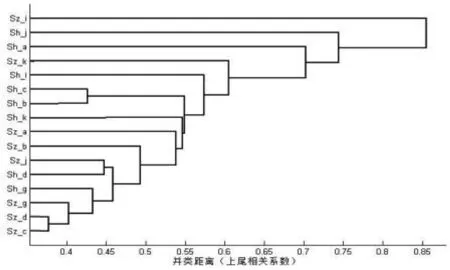
图1 上尾部相关系数的聚类谱图

图1最后4次并类不一致系数的增幅依次为0.1451、0.5539、-0.1161、0.2547。倒数第3次并类不一致系数有大幅增加，倒数第4次并类效果较好。故考虑上尾相关时，16大板块可分为4类：第1类是Sh_a；第2类是Sh_j；第3类是Sz_i；第4类是其他。当股价高涨时，为降低投资风险，可将资金以适当比例分散投资于这4大类中。

图2最后1次并类的不一致系数有大幅增加，倒数第2次并类效果较好。故考虑下尾相关时，16大板块可分为8类：第1类是Sh_b；第2类是Sh_j；第3类是Sh_a；第4类是Sz_a；第5类是Sz_i；第6类是Sz_j；第7类是Sz_k；第8类是其他。当股价猛跌时，为降低投资风险，可将资金以适当比例分散投资于这8大类中。

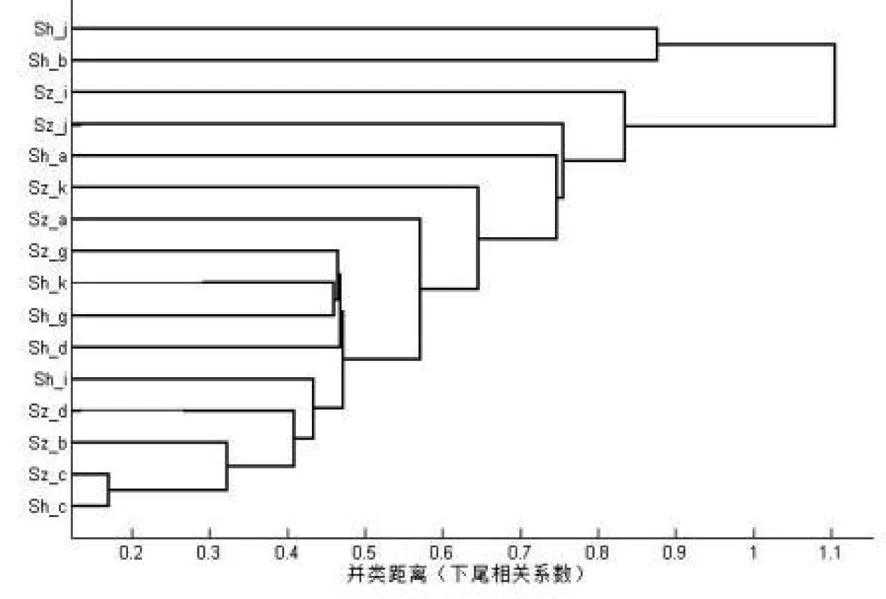
图2 下尾部相关系数的聚类谱图

综合考虑上下尾相关情况时，发现上尾聚类结果包含在下尾聚类结果中，且下尾最终聚类结果为8类，多于上尾的3类，说明股价高涨时板块间的联动性更强，市场对利好消息的反应更为敏感。两市农、林、牧、渔板块下尾相关性不显著，两市金融业板块下尾相关性也不显著，进一步说明市场对利空消息的反应相对较慢。

聚类谱图只是直观、定性地给出了16大板块的大致分类。下面本文利用马科维茨投资组合理论中著名的均值-方差分析方法确定出16大板块最优投资组合策略。首先计算16大板块上、下尾相关系数的方差-协方差矩阵，然后通过求解二次规划得到最优投资组合策略,如表5所示。

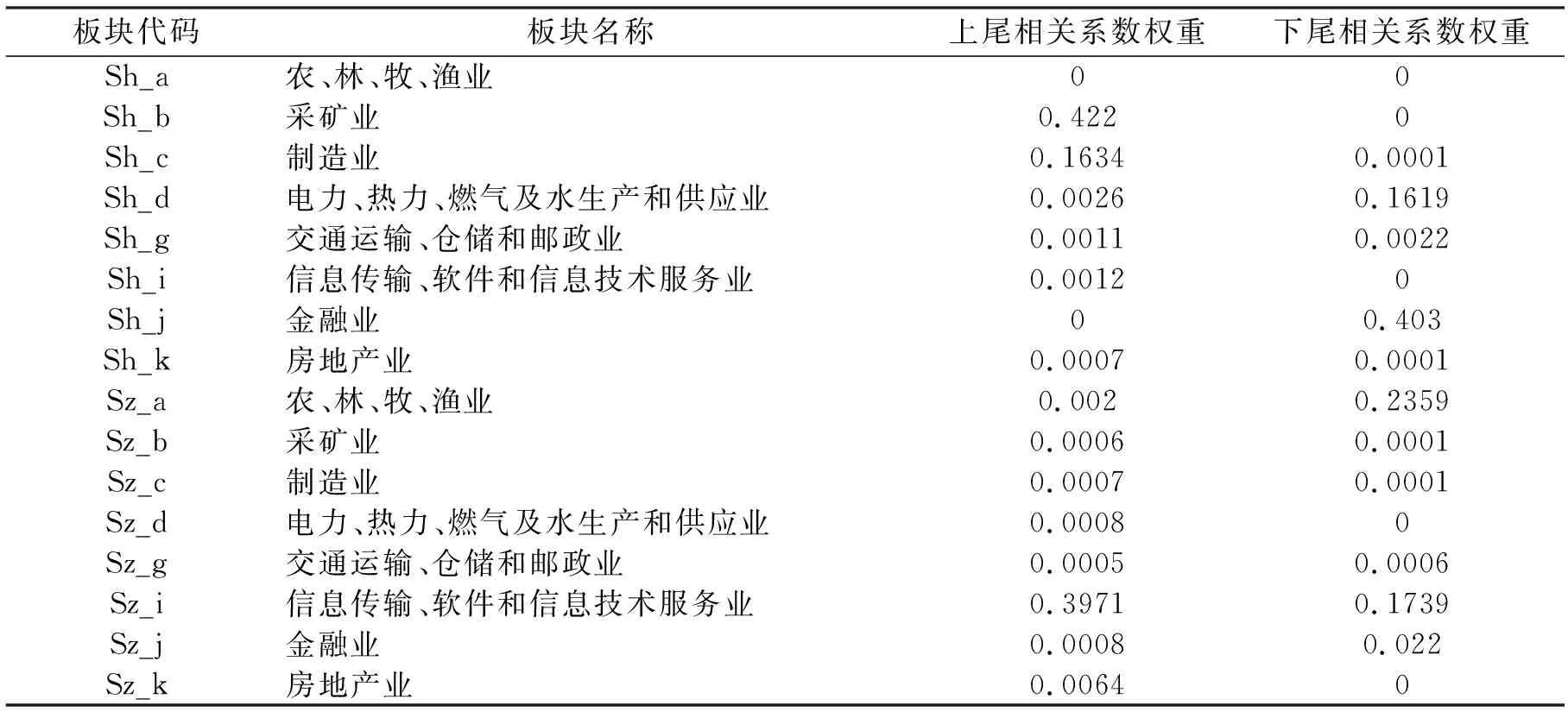
表5 沪深两市16大板块最优投资组合

由表5可见，考虑上尾相关时，最优投资组合为：沪市采矿业42.2%，深市信息传输、软件和信息技术服务业39.7%，沪市制造业16.3%，深市房地产业0.64%，其余板块股票可少量持有或不再持有；考虑下尾相关时，最优投资组合为：沪市金融业40.3%，深市农、林、牧、渔23.6%，深市信息传输、软件和信息技术服务业17.4%，沪市电力、热力、燃气及水生产和供应业16.2%，深市金融业2.2%，其余板块股票可少量持有或不再持有。

4 结语

金融资产的相关性分析，特别是尾部相关性分析不仅有助于投资者和投资机构对资产更好地进行组合投资，而且有利于投资者和投资机构规避金融市场的流动性风险。以往文献很少研究股票市场板块间的相关性，本文基于M’-Copula-t-GARCH模型对沪深两市16大板块尾部相关性进行了实证研究，并据此给出了投资组合建议。