运用启发式算法的木板最优切割方案
2021-04-11徐宗煌徐剑莆李世龙林慧雅许美燕
徐宗煌,徐剑莆,李世龙,林慧雅,许美燕
(1.福州理工学院 应用科学与工程学院,福建 福州 350506;2.福州理工学院 计算与信息科学学院,福建 福州 350506;3.福州理工学院 商学院,福建 福州 350506 )
本文讨论的问题和应用的数据均来源于2019 年第十六届五一数学建模竞赛B 题.木板切割,实际上是属于二维下料优化问题,其主要应用在机械加工、切割下料以及工厂车间布局等制造生产加工领域[1].由于二维下料优化问题自身的复杂性,在实际生产应用中,往往会造成原料的大量浪费,从而提高产品成本.因此,如何提高原材料的利用率而节省产品加工成本,具有非常重要的实用价值.
从数学计算复杂性理论看,木板切割的优化问题属于NP 完全问题[2].目前,国内外许多学者对二维下料优化问题进行了诸多研究,主要是采用启发式算法、禁忌搜索算法、遗传算法以及模拟退火算法等大量的优化方法.本文基于循环嵌套启发式贪心算法、遗传模拟退火算法以及价值修正的顺序启发式算法等优化方法,分别对切割单个产品、多个产品以及考虑生产任务需求的木板切割优化方案进行了探究分析.
1 模型假设
在问题求解过程中,考虑到实际情况与简化计算的需要,提出以下假设:1)将木板和产品的长度和宽度均看作是矩形;2)在切割过程中,木板厚度和割缝宽度忽略不计;3)该批木板的材质分布均匀,不会影响切割产品的效果;4)所给的木板和产品尺寸均为真实有效.
2 单个产品木板最优切割方案
2.1 研究思路
在一块木板上只切割P1 产品,首先利用循环嵌套式的启发式算法,使得沿木板四条边方向上的利用率达到最优;再结合Packing 问题的贪心算法,以木板利用率最高为优化目标,逐层优化,最终得到单个产品的最优切割方案.
2.2 模型建立
设木板尺寸为L×W,P1 产品尺寸为l×w,要使木板切割尽可能多的P1,应尽量利用l 和w 的各种组合,使得L 和W 方向上的利用率尽可能高,即对L 和W 边上同时对l 和w 进行组合优化[3],使得木板四条边的尺寸利用达到最优.其优化示意图如图1.
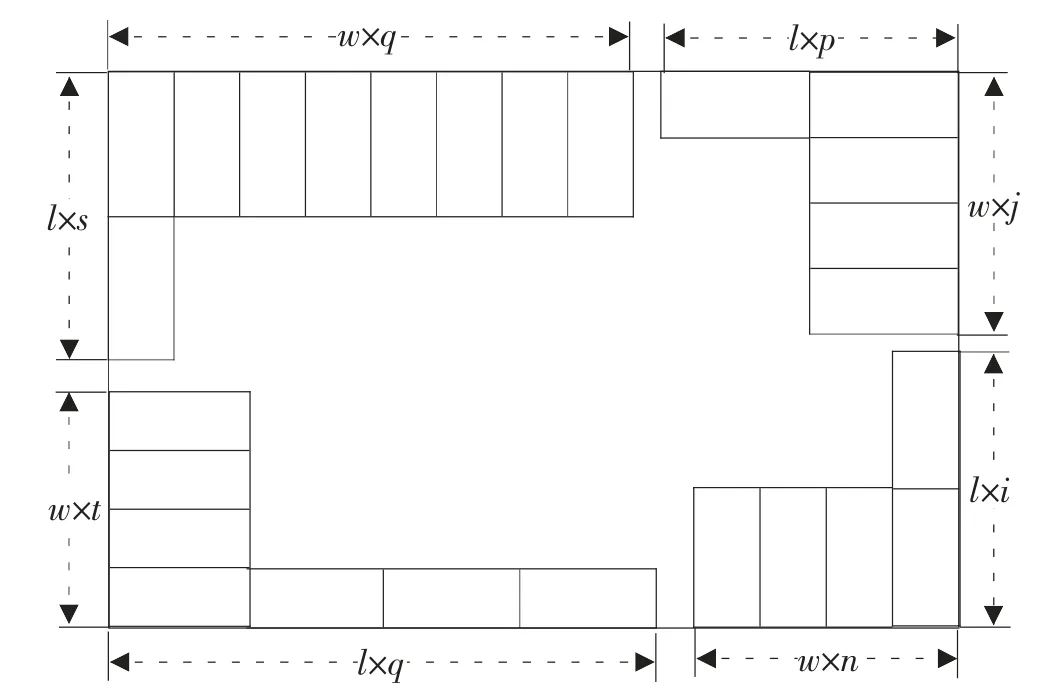
图1 基于循环嵌套启发式算法的优化示意图
2.2.1 确定目标函数 显然,最优切割方案的目的是为了使木板的利用率最高,令μ 为木板的利用率;N 为木板切割P1 产品的数量,则P1 产品的最优切割方案的目标函数为

2.2.2 确定约束条件 如图1 所示,当木板上L 边上切割了m 个l 边,则可以再切割n=[(L-ml)/w]个w边;而当右W 边上切割了i 个l 边,则还可切割w 边的个数为j=[(W-il)/w];同理,可根据木板上L 边上l 的个数p 和右W 边上l 的个数s 分别确定各自边上w 的个数q 和t,结合问题的要求与已知条件,主要考虑以下3 个约束条件.
1) 约束条件1
基于保证木板在L 边和W 边的利用率,即要保证木板四条边上所留的空隙不能再放入P1 产品的较小边,即w 边,则该约束条件为

2) 约束条件2
基于i 和t 以及p 和n 之间的约束条件为

式(3)中,“[ ]”表示取整符号.
3) 约束条件3
基于保证在切割时不能出现P1 产品之间发生干涉的情况,该约束条件为

2.3 问题求解
基于以上分析,利用在货物装载和木材下料等领域应用广泛的二维矩形Packing 问题的贪心算法[4-7],同时结合循环嵌套式的启发式算法[8-9],以木板利用率最高为优化目标,由外及里,逐层优化,如图2 所示.利用MATLAB 编程得到P1 产品的最优方案切割图,如图3 所示.最优的切割方案为:P1 产品的数量为59 件,木板利用率为98.297 9%.
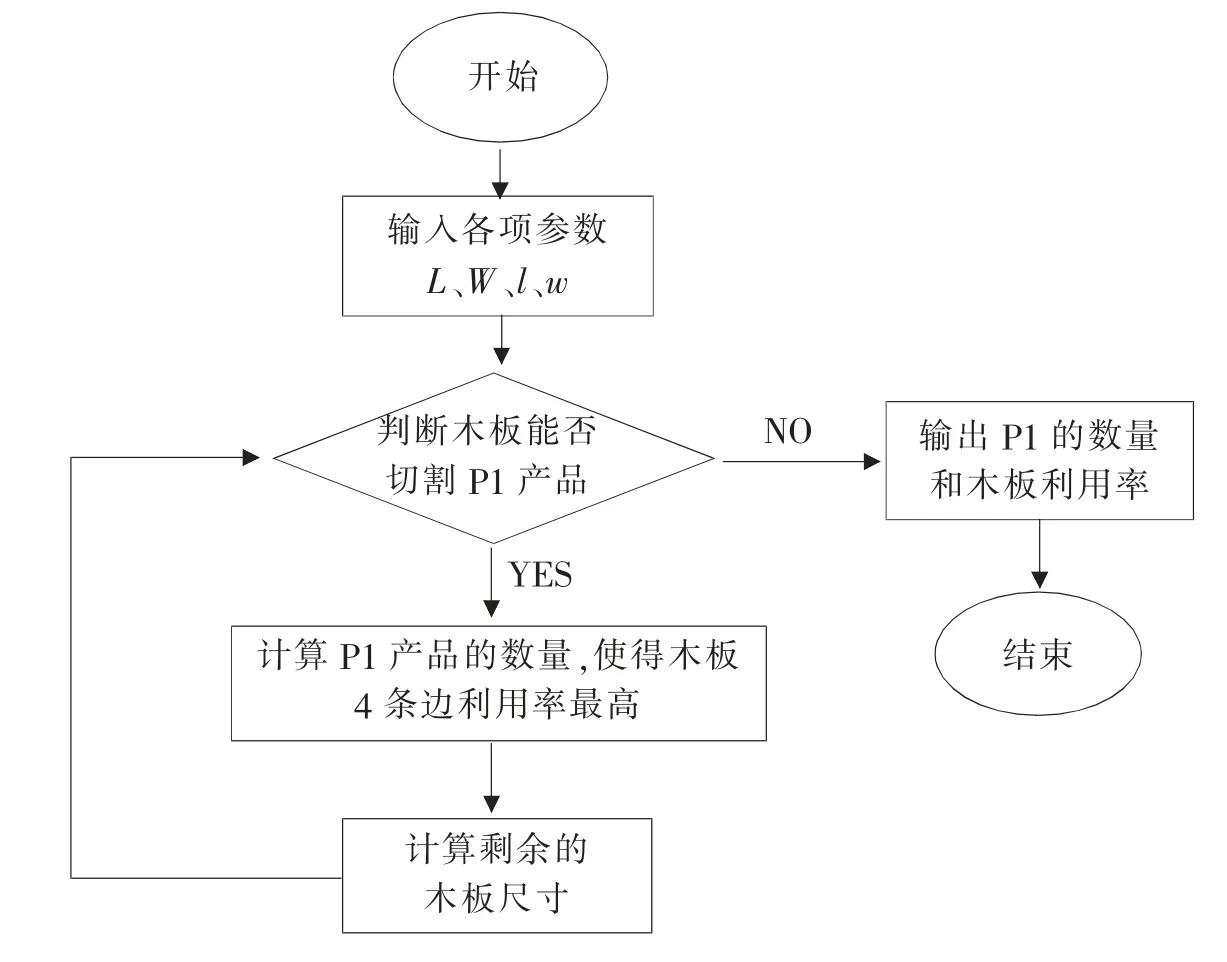
图2 模型主程序流程图
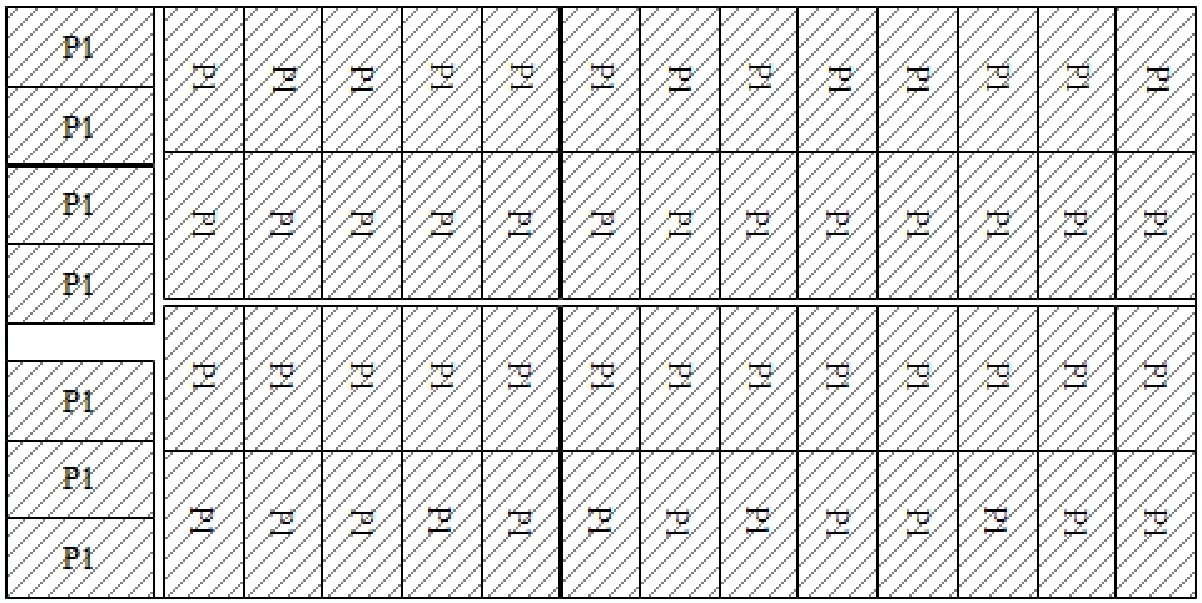
图3 P1 产品的最优方案切割图
3 多个产品木板最优切割方案
3.1 研究思路
考虑到P1 和P3 产品的切割次序和切割方向是影响木板切割利用率最重要的因素,将遗传算法和模拟退火算法结合起来形成自适应遗传模拟退火算法[10-11].这样不仅可以大大提高计算的效率,而且可以避免陷入局部最优,从而在木板上切割P1 和P3 产品可以取得比较理想的结果,同时给出木板利用率由高到低排序的前3 种切割方案.
3.2 模型建立
3.2.1 确定目标函数 通过以上分析,显然,最优切割方案使木板的利用率最高.令μ为木板的利用率,Ni为切割第i 种产品的数量,则最优切割方案的目标函数为

3.2.2 确定约束条件 同样的,已知木板尺寸为L×W,产品尺寸为li×wi(i=1,3),即P1 产品尺寸为l1×w1,P3 产品尺寸为l3×w3,Ni为切割第i 种产品的数量.而mi表示第i 种产品横放时所需的行数,ni表示第i种产品竖放时所需的行数,xi表示竖放时一行的产品个数,yi表示横放时一行的产品个数,ri=0 表示该产品的竖放方式,ri=1 表示该产品的横放方式.结合问题的要求与已知条件,主要考虑以下两个约束条件.
1) 约束条件1
基于保证木板在L 边和W 边方向上,P1 和P3 产品尺寸和不能超过木板尺寸,则该约束条件为

式(6)中,k 表示有k 种产品.
2) 约束条件2
基于在切割P1 和P3 产品时,其数量关系必须满足以下限制约束条件

3.3 问题求解
利用自适应遗传模拟退火算法[12]从一组随机产生的初始解(初始群体)开始全局最优解的搜索来产生P1 和P3 产品的切割次序以及切割方向,其主要步骤如下.
3.3.1 设计基因编码 为降低算法复杂性,采用十进制编码方式对木板切割进行优化,设有n 个切割产品,则切割产品次序编号为1,2,…,n,第i 个切割产品的编号为i,则这n 个待切割产品的一个排列为δ=[x1,x2,…,xn],其中xi表示排列δ 中第i 个切割产品的编号.由于各个产品在切割过程中可以90°旋转,因此在排列δ 中为各个切割产品增加旋转变量ri,即

3.3.2 设计适应度函数 问题的目标在于提高木板的利用率,因此采用最优切割方案的目标函数式(5)作为适应度函数,即

式(9)中,Xi为种群中的某一个个体,代表唯一的产品切割方案,因此f(Xi)即为切割序列Xi的木板利用率,f(Xi)值越大,表明木板切割方案最优.
3.3.3 交叉和变异操作 采用一种自适应调整交叉和变异概率的方法来改善算法的行为和性能,同时利用以下概率调整公式

来调整种群中的某一个个体Xi的交叉和变异概率.式(10)中:Pc和Pm分别为该算法的交叉和变异概率;fb(X)、fw(X)和f(Xi)分别表示每一代所有个体中最优、最差个体以及Xi的适应度值.
3.3.4 模拟退火操作 对经过交叉和变异操作后生成的新种群个体Xi,基于Metropolis 的接受准则,计算新个体被接受的概率,其接受准则为

式(11)中,fi(T)为个体基本变换前适应度;fj(T)为个体基本变换后适应度;T 为当前温度.
3.3.5 构造初始种群的个体 一半通过优先级函数产生,一半通过随机数作为优先级产生,优先级函数公式为

式(12)中,Pi为第i 个产品基因优先级;pr为该产品长宽比值所占权重;ps为产品面积所占权重且满足pr+ps=1;函数生成的随机数Ri∈(0,1).
利用MATLAB 编程,将木板、P1 和P3 产品的尺寸输入,可得到P1 和P3 产品的切割方案,图4 所示为木板利用率由高到低排序的前3 种方案切割图.木板利用率前3 的切割方案为:1) P1 产品的数量为0件,P3 产品的数量为48 件,木板利用率为99.172 3%;2) P1 产品的数量为43 件,P3 产品的数量为13件,木板利用率为98.500 0%;3)P1 产品的数量为59 件,P3 产品的数量为0 件,木板利用率为98.297 9%.
4 考虑生产任务需求的最优切割方案
4.1 研究思路
在生产任务需求一定的情况下,考虑到顺序启发式算法可以在木板切割产品过程中,随着产品的生成数量不断的增加,其切割所需剩余量也发生相应变化.但传统的SHP 算法[13-14]在生成木板切割方案时存在一定的缺陷,它容易使得好的切割方案在前面出现,而导致后面的切割方案的材料利用率偏低.采用顺序价值修正策略[15-17],依次生成各个切割方案,并根据该切割方案中产生的产品数来修正产品生产任务剩余量,重复此过程,直至所有产品剩余的生产任务均为零,从而得到木板总利用率最高的切割方案,其主要流程图如图5 所示.

图5 顺序启发式算法流程图
4.2 模型建立
假设初始化各个产品的价值为产品各自的面积,则生成切割方案可根据单位面积价值的大小确定,且产品的当前待切割方案为Pj=[a1j,a2j,…,anj],aij为该方式中含产品i 的个数,i=1,2,…,n.而每生成一个切割方案都通过

式(13)中aij>0,si为产品i 的面积;p>1 为控制参数;g1和g2为价值修正的控制系数,g1+g2=1,且满足

式(14)中,di为产品i 的生产任务为产品i 剩余的工作任务需求;Ω 为随机产生,Ω⊂且
式(13)可写成

4.3 问题求解
通过以上分析,利用MATLAB 编程,将木板的尺寸、P1~P4 产品的尺寸以及生产任务输入,得到木板总利用率最高的切割方案,图6 所示为完成P1~P4 产品生产任务的木板切割方案图.表1 为考虑生产任务需求的最优切割方案.

图6 最优方案切割图
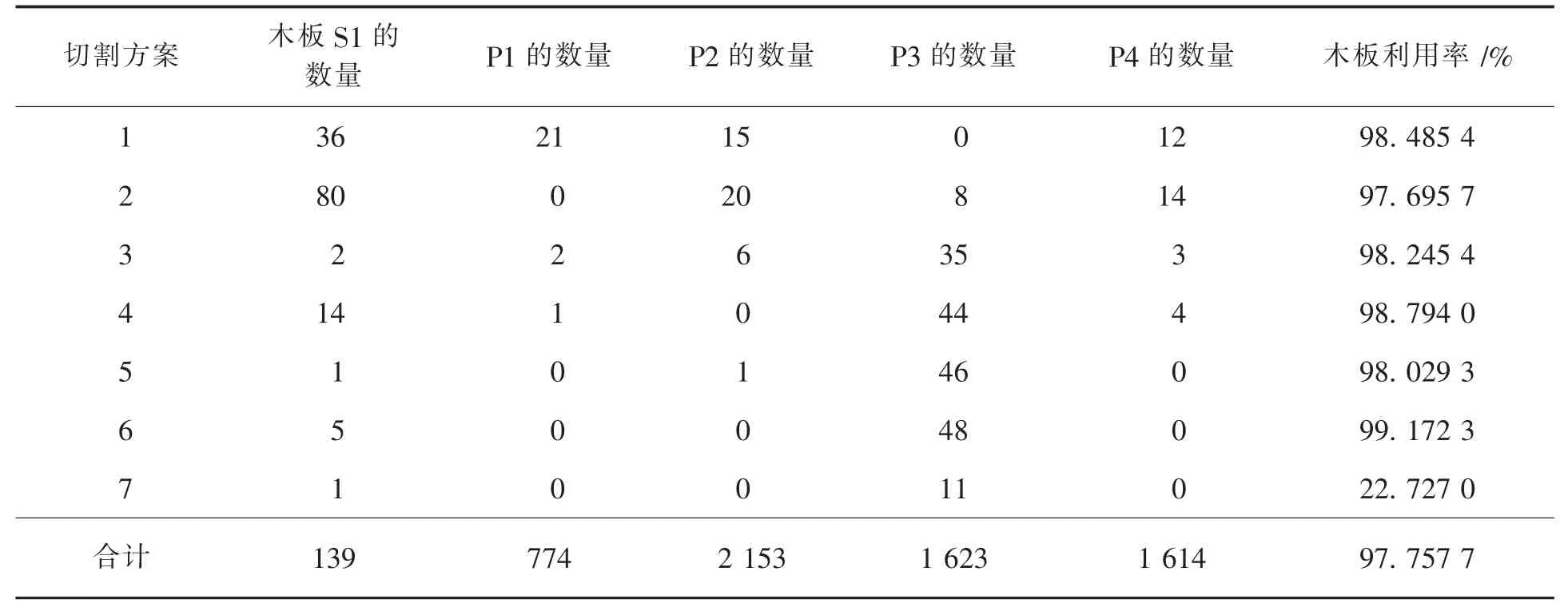
表1 考虑生产任务需求的最优切割方案
由表1 可以看出,当需要同时完成P1~P4 产品的生产任务时,需要7 种切割方案才能使木板的总利用率最高.此时木板的数量为139 块,总利用率为97.757 7%.
5 结论
本文基于循环嵌套启发式贪心算法、遗传模拟退火算法以及价值修正的顺序启发式算法等优化方法,分别对切割单个产品、多个产品以及考虑生产任务需求的木板切割优化方案进行了探究分析.在保证思路严谨的前提下,基于启发式算法化繁为简,大大降低了算法的计算复杂度,可操作性强,最终得到较为理想的切割方案,对机械加工、切割下料以及工厂车间布局等制造生产加工的过程有一定理论指导和参考价值.
