混合局部因果结构学习

王雲霞，曹付元+，凌兆龙

1.山西大学计算机与信息技术学院，太原 030006

2.山西大学计算智能与中文信息处理教育部重点实验室，太原 030006

3.安徽大学计算机科学与技术学院，合肥 230601

因果关系发现在计算机科学领域发挥着重要的作用，比如面向多源数据的因果关系发现[1-3]，选择与类别属性有因果关系的特征来增强机器学习模型的泛化能力与可解释性[4]，利用因果理论解决复杂的机器学习问题[5-6]等。因果结构学习是识别变量之间因果关系的一个学习过程，而挖掘一个与数据拟合程度较好且包含所有变量的全局（或完整）的贝叶斯网络可以学习变量之间的因果关系[7-8]。但是大数据时代的到来使得越来越丰富的数据为因果结构学习带来更多信息的同时也带来了相应的挑战。一方面丰富的数据含有更多的信息，为因果结构学习提供了更多的数据支撑，另一方面数据的维度越来越高，其在计算时间和空间存储上消耗较大，全局因果结构学习将变得困难甚至在更大型的数据集上无法运行。此外，如果仅仅对高维数据中某一部分变量之间的因果关系感兴趣时，构建全局网络是浪费时间与空间的。因此相对于全局因果结构学习方法，局部因果结构学习方法可以在高维数据中挖掘任意感兴趣变量的局部因果结构，且从计算资源与存储资源的角度，局部因果结构挖掘更高效且更具有实际意义。

Silverstein 等人提出第一个局部因果结构学习算法，即LCD（local causal discovery）算法[9]，该算法利用条件独立性学习四个变量之间的因果关系。基于LCD 算法，Mani 等人提出BLCD（Bayesian local causal discovery）算法[10]，它首先学习目标变量的马尔科夫毯（Markov blanket，MB），然后学习MB 中的Y 结构来进行局部因果结构的学习。但是上述的两个算法并没有识别到目标变量的直接原因和直接结果。基于LCD 算法和BLCD 算法的不足，Yin 等人提出了PCD-by-PCD（parents，children and some descendants）算法[11]，该算法首先利用MMPC（max-min parents and children）算法[12]学习目标变量的PC 集，然后利用条件独立性测试寻找其中的V 结构，递归地推出PC集中变量之间的因果关系。Gao等人提出CMB（causal Markov blanket）算法[13]，其基本思想与PCD-by-PCD算法一致，该算法首先调用HTION-MB 算法[14]寻找目标变量的MB，然后利用条件独立性测试和Meek规则递归地推导边的方向。但是上述两个算法的精度相对不是很高，且有限样本下其精度更差。其原因是一方面受到PC（parents and children）发现结果的影响，另一方面是边的定向过程中对V 结构的依赖性也会使得算法精度不稳定。

目前已有的局部因果结构学习算法分为两个步骤：步骤1 是发现目标变量的MB 或PC，即目标变量的局部结构骨架[15-16]；步骤2 是对PC 集中的变量确定其与目标变量之间的因果关系。两个步骤的结果都对最终的算法产生一定的影响。

步骤1 中PCD-by-PCD 算法和CMB 算法分别调用基于限制的因果关系发现算法：MMPC 算法和HTION-MB 算法来发现目标变量的局部结构骨架。而这两个算法都是直接利用条件独立性学习MB/PC，其对数据样本大小有一定的要求，当数据样本没有达到MB/PC 尺寸的指数级数量时，算法所用的条件独立性测试将有较高的错误率，进而导致这两个方法的精度较差。为了解决上述问题，本文在基于限制方法的基础上结合打分方法来缓减有限样本问题，原因是打分方法具有更强的容错性，能够通过搜索一个明显较小的空间收敛到一个更高质量的网络，且基于分数的方法在可能的图结构中有更强的先验性，可以缓减影响算法精度的有限样本问题。而单纯的采用打分的方法如S2TMB（score-based simultaneous Markov blanket）算法[17]，由于其是对每一个变量逐一考虑进行打分，时间效率极低。因此本文结合两种思想来综合提高步骤1 性能。

步骤2 中PCD-by-PCD 算法和CMB 算法都是直接利用条件独立性测试寻找V 结构，然后利用Meek规则确定边的方向来得到目标变量的局部结构。一方面因为V 结构依赖于基本网络结构，而算法结果又依赖于V 结构的发现即当正确发现的V 结构很多且与目标变量有关系时，最终算法的精度相应较高，当正确发现的V 结构很少且与目标变量没有关系时，那么最终算法的精度将会大幅度降低。因此这两个算法最终得到的结果精度是要依赖于基本网络中V 结构的发现[18]。另一方面同样由于有限样本等影响，条件独立性测试将存在一定的错误性，这也就意味着V结构发现以及Meek 规则的使用将存在一定的错误性，从而导致最终算法精度相对不高。因此为了降低对V 结构的依赖性且缓减有限样本问题，同时提高相对于打分方法的时间效率，本文结合限制与打分方法对已有的局部因果结构学习算法进行改进来提高算法的精度。

本文提出一种新的基于打分和限制相结合的混合局部因果结构学习算法（hybrid local causal structure learning，HLCS）。步骤1 对基于打分的PC 发现算法进行了改进，通过加入限制思想降低所测试的节点数目，且输出目标变量与其PC 集变量的定向结果，提出一种基于打分和限制相结合的PC 发现算法SIAPC（score-based incremental association parents and children）；步骤2 通过利用SIAPC 算法得到的定向结果和对部分数据集打分得到的定向结果的交集来确定边的方向，之后结合条件独立测试来降低对V 结构的依赖性。实验结果验证了本文方法相对于目前的方法在精度方面有显著提高，且有效缓减了数据效率问题。

1 背景知识

为方便可读，本文用V=(X1,X2,…,Xn)表示n个观测变量（节点），P是V上的一个离散的联合概率分布，G代表一个有向无环图DAG 。如果满足马尔科夫条件，则称为一个贝叶斯网络。在一个贝叶斯网络中，Xi⊥Xj和分别表示变量Xi、Xj之间的独立性和依赖性，Xi⊥Xj|Z表示在集合Z的条件下，变量Xi条件独立于Xj，其中Z⊆V{Xi,Xj}，同理表示在Z的条件下，变量Xi条件依赖于Xj。下面给出一些相关的定义。

定义1（马尔科夫条件）[19]给定一个有向无环图G，马尔科夫条件在G中成立当且仅当G中的每一个节点都独立于它的非后裔节点的任何子集。

马尔科夫条件使得贝叶斯网络对一组变量V的联合概率实现分解化，即P(V)可以分解为G中在给定父集条件下变量条件概率分布的乘积，其中PA(T)是G中变量X的父集，则P(V)被表示为：

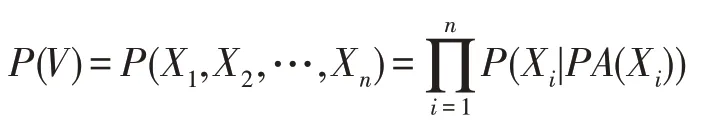
定义2（条件独立性）[19]两个不同的变量Xi,Xj∈V被认为在给定变量子集Z⊆V{Xi,Xj}下是条件独立的当且仅当P(Xi,Xj|Z)=P(Xi|Z)P(Xj|Z)成立，否则Xi、Xj被认为在变量子集Z下条件依赖。

定义3（d-分离）[20]在一个有向无环图G中，一条路径π被集合Z⊂Vd-分离当且仅当（1）π中包含Xi→Xk→Xj（Xi←Xk←Xj）或Xi←Xk→Xj，其中中间节点Xk属于Z即Xk∈Z，或（2）π中包含一个V 结构Xi→Xk←Xj，此时中间节点Xk不属于Z，且Xk的子孙节点也不在Z中。集合Z被认为d-分离Xi，Xj当且仅当Z阻隔了从Xi到Xj的每条路径。

定义4（忠实性假设）[21]给定一个贝叶斯网络，G忠实于P当且仅当P中的每个条件独立都受G和马尔科夫条件的影响。P是忠实的当且仅当G对P忠实。

定义5（马尔科夫毯）[21]忠实性假设下，在一个贝叶斯网络中，一个变量T的马尔科夫毯MB(T)是唯一的且包含其父母PA(T)、孩子CH(T)和配偶SP(T)（变量的孩子的其他父母），即MB(T)=PA(T)⋃CH(T)⋃SP(T)。

定义6（近似PC 集）在一个贝叶斯网络中，设CSet(T)为与变量T相关的节点集且Xi,T∈V），若T⊥Xi|Xk且Xi∈CSet(T),Xk∈CSet(T){T,Xi}，则从CSet(T)中去掉Xi，最终剩下的节点集定义为目标变量T的近似PC 集，记作SPC(T)。

定义7（环绕结构）给定一个贝叶斯网络，忠实性假设下，若存在三个以上的节点构成的结构满足以下条件：（1）节点数目等于边的数目；（2）该结构的每一节点都有两条边相连；（3）Xi⊥Xj|Z且，Z⊆V{Xi,Xj}，则称该结构为环绕结构。

2 基于打分和限制相结合的混合局部因果结构学习算法

局部因果结构学习方法通常包括两个步骤：（1）挖掘目标变量的MB/PC；（2）迭代进行边的定向，得到目标变量的局部结构。图1 展示了一个因果网络结构，假设目标变量为T，则由图1 可知T的PC 集为PC(T)={N,A,L,J,B,C}，而{T,A,D,L}和{T,B,F,M,C}构成的结构是定义7 的环绕结构。

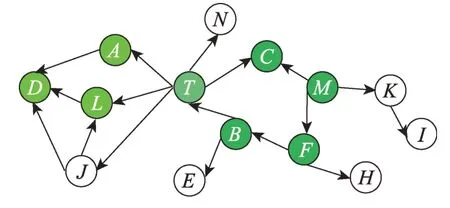
Fig.1 Causal network structure 1图1 因果网络结构1

理论上基于限制的方法可以得到正确的PC/MB，但是有限样本问题导致的条件独立性测试存在一定的错误性，因此最终得到的目标变量的PC/MB 可能不是完全正确的。而基于打分的学习方法使用带分数标准的BN（Bayesian network）结构学习算法来查找局部结构，其在可能的图形结构上具有更强的先验性，且打分方法MMHC（max-min hill-climbing）在有限样本中可以收敛到一个更高质量的网络。因此为了解决由有限样本产生的条件独立性导致的错误以及由打分方法本身产生的时间效率问题，本文结合基于限制和基于打分-搜索的方法，综合考虑PC/MB 发现，提出SIAPC 算法。

以图1 为例，由于马尔科夫等价类的存在，已有的局部因果结构学习算法在结构{T,C,F,M,B}中，无法确定T和{B,F,M}之间的关系；同理在结构{T,A,D,L}中，也无法确定T和{A,L}之间的关系。因此已有的局部因果结构学习算法在面对上述结构中，需要寻找更多的V 结构来判断边的方向，但是V 结构依赖于基本网络结构，因此算法最终得到的结果精度要取决于V 结构的发现。而打分方法因为在可能的图形结构上具有更强的先验性，其可以降低算法对V结构的依赖性，所以为了解决已有算法对V 结构依赖问题，缓减数据效率问题，本文结合打分方法对基于限制的局部因果结构学习算法进行改进，提出混合的局部因果结构学习算法HLCS。

2.1 挖掘目标变量的PC 集

设与变量X依赖的集合为CSet(X)，与变量X独立的集合为CC(X)，由于变量X的PC 集PC(X)是与X直接相连的节点集，因此PC(X)是CSet(X)的子集，即PC(X)⊆CSet(X)。由定义3，在CSet(X)中发现存在集合S可以阻断X和Y（Y∈CSet(X){S,X}）之间的路径，则Y一定不属于PC(X)，也就是可以被阻断的节点不是和X直接相连的节点，因此可以对Y∈CSet(X)与X之间的路径用d-分离进行测试，得到变量X的最终的PC 集PC(X)。

在图2 中，设蓝色节点为目标节点T，绿色节点表示PC(T)={A,B,C,L}，经分析绿色节点和黄色节点构成CSet(T)={A,B,C,L,D,E,F,H}，此时对于目标节点T来说，D被{A,L}阻断，E被B阻断，H被F阻断，F被B阻断，因此CSet(T)中剩下的节点为{A,B,C,L}，即最终变量T的PC 集为PC(T)={A,B,C,L}。

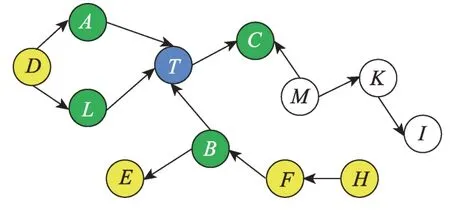
Fig.2 Causal network structure 2图2 因果网络结构2

但是上述思想存在以下问题：（1）非常依赖条件独立测试的正确性且仅仅关注CSet中的变量的情况；（2）当近似PC 集的长度很大时，所需要的条件独立测试次数将呈指数级增长，即设ns=|SPC|。由于条件集长度为1 时CSet可以去掉大部分在其中的节点，之后对剩下的节点集也就是近似PC 集考虑条件集长度为i=2,3,…,ns，此时相对于CSet的长度仅仅去掉少部分节点，因此本文计算条件独立测试的次数，直接使用ns作为近似测试次数，即近似结果为：

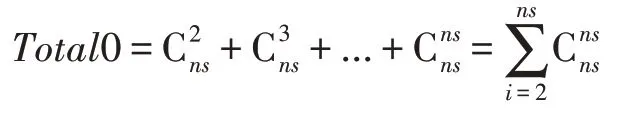
经分析，上述思想总的独立性测试次数为Total=|V|+|CSet|2+Total0，但是这种方法的条件独立性测试次数相对较多，最终的结果精度不是很高。为了进一步减少条件独立测试次数，本文直接将Xi∈CSet(T)作为条件集测试Xj∈CSet(T)和T之间的独立性，进而得到T的近似PC 集SPC(T)。此方式可以使条件独立测试次数减少到Total=|V|+|CSet|2，且最终保留较少节点在SPC(T)中（PC(T)⊆SPC(T)）。同时为了缓减对条件独立测试正确性的依赖，本文采用已有基于打分-搜索的方法对CC(T)与SPC(T)中的变量共同考虑，来寻找最终的PC(T)。对{CC(T),SPC(T)}共同考虑的原因是：（1）目标节点T与X∈SPC(T) 和Y∈CC(T)可能会构成V 结构。如图2 所示，C是T的PC 节点，且＜T,C,M＞构成V 结构，可以进一步确定C是T的PC 节点。（2）由于SPC(T)是对CSet(T)的精简，每次对数据集DATA{T,X,PC(T)},X∈{SPC(T),CC(T)}进行打分，得到的PC(T)的长度都较小，这使得算法效率更高。本文采用基于打分-搜索的全局因果结构学习算法MMHC 进行打分判定，且其使用的分数准则为BDeu。

基于上述分析，本文提出以下改进的PC 发现算法SIAPC，如算法1。

算法1SIAPC

输入：数据集DATA，目标变量T，独立性指标w0。

输出：PC为T的PC集，CSet为与T依赖的集合，SPC为T的近似PC 集，PA为T的父集，CH为T的子集。

2.2 迭代进行边的定向

由于上述的PC 发现算法用打分方法只能确定和目标变量T相连的一部分边的方向，且由于是对一部分数据集进行打分，最终得到错误的边定向结果是相对较多的，由此在边的迭代定向过程中要进行边方向的进一步确定与修正；在迭代边定向过程中用到的原则就是寻找V 结构，如图3 中的＜A1,T1,B1 ＞，＜A2,T2,B2 ＞构成V 结构，但A1、B1 存在依赖关系，A2、B2 存在依赖关系，即＜Ai,Ti,Bi＞构成V结构，Ai、Bi之间存在依赖关系（i=1,2,…,n）。此时可以检测＜Ai,Ti,Bi＞为V 结构，但是对于V 结构之外的路径判断不了边的方向。面对上述结构，已有的基于限制的方法会进一步寻找更多的MB 或PC集去确定更多的V 结构，算法结果依赖于发现的V 结构且在大部分网络中性能较低。

Fig.3 Two examples of surround structure图3 环绕结构的两种示例

基于上述问题本文结合打分方法进行改进。由于基于打分-搜索的方法在可能的图形结构上具有更强的先验性，其在实践中表现相对比较稳定，尤其是在样本量较小的情况下，基于打分-搜索的方法MMHC 算法将会收敛到一个更高质量的网络，且与基于约束的方法相比，基于打分-搜索的因果结构发现方法的探索相对较少，因此其能更好地处理对V 结构的依赖问题。由此算法总体思想是：首先通过SIAPC 算法得到目标节点T的部分父集和子集；然后确定相关的数据集Z进行打分，得到目标节点T的部分父集和子集；之后取二者的交集作为确定的T的父集和子集；最后利用已有的基于限制的方法通过寻找V 结构以及利用Meek 规则来进行修正。

在选取数据集方面，本文目的是选取与目标变量最相关的变量集进行打分，若变量集长度太大则采用打分方法的时间效率很低，长度太小则影响打分结果，因此为了降低时间效率且尽量不损失精度，本文选择部分数据集Z的方式如下：（1）若SPC(T)长度小于一个给定的参数ss，如果其不为空则选取{SPC(T),T}作为新的数据集Z，否则选取{CSet(T),T}作为新的数据集Z；（2）若SPC(T)长度大于ss，则选取PC(X)（X∈PC(T)）的并集作为新的数据集Z；（3）最后得到的新的数据集Z需要满足|Z|＞zs，若不满足，则加入PC(X)到新的数据集中（X∈Z）。对于ss和zs的选取问题，本文进行人工选取然后用实验进行测试，其中ss选用10、20、30、40，得到ss=20 的实验结果较好；对于zs，本文选用4、5、6、7，得到zs=5 的实验结果较好。

2.3 基于打分和限制相结合的混合局部因果结构学习算法

本文规定ID表示其他变量相对于目标变量的因果识别[12]，若T是目标变量，X是其他变量且X∈PC(T)，则ID(X)=1 说明X相对于T来说，X是T的直接原因，ID(X)=2 说明X是T的直接结果，ID(X)=3 说明X与T直接相连，但是方向不确定。本文提出基于打分-搜索方法和基于限制方法结合的混合局部因果结构学习算法HLCS，如算法2。

算法2HLCS

输入：数据集DATA，目标变量T，独立性指标w0，数据集选取参数ss和zs。

输出：PA为T的父节点集，CH为T的子节点集，UN为T的未定向节点集，PC为T的PC 集。

算法3HLCS_sub

输入：数据集DATA，目标变量T，当前ID，独立性指标w0，数据集选取参数ss和zs。

输出：ID相对于T的因果识别。

3 实验及其结果

3.1 数据集

为了验证算法的有效性，本文选取https://pages.mtu.edu/～lebrown/supplements/mmhc_paper/mmhc_index.html 上的10 个基准网络数据集作为测试数据，具体信息如表1。

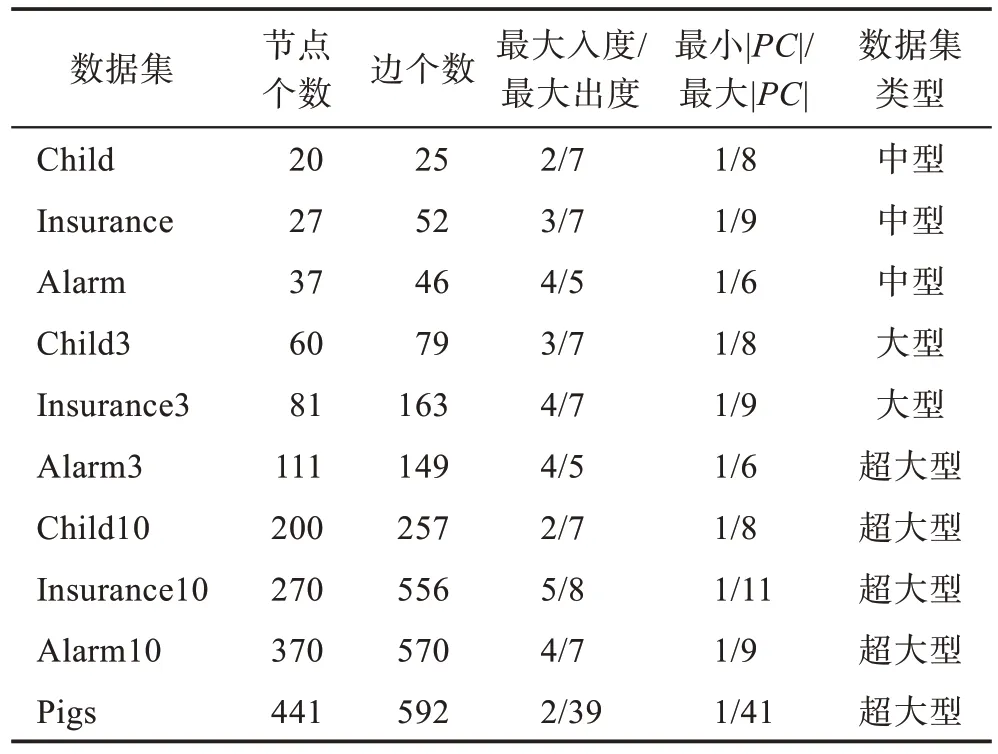
Table 1 Data information of 10 benchmark networks表1 10 个基准网络数据信息

3.2 评价指标

为了评价算法的性能，针对两组实验分别给出了不同的评价指标，具体如下：

（1）PC 发现算法的评价指标[2]

①Precision：算法输出正确点的数量（和基准网络对比）/算法输出的点的数量。

②Recall：算法输出正确点的数量（和基准网络对比）/基准网络中真正的点的数量。

③F1：(2×Precision×Recall)/(Precision+Recall)。

④Distance：

⑤Time：运行每个点的平均时间，单位为秒（s）。

其中③和④表示的是算法的精度，⑤表示算法的时间效率。

（2）局部因果结构学习算法的评价指标[8]

①ArrPrecision：算法输出中定向正确的边的数量（和基准网络对比）/算法输出的边的数量。

②ArrRecall：算法输出中定向正确的边的数量（和基准网络对比）/基准网络中边的数。

③SHD：算法输出中定向错误的边的数量（和基准网络对比）。

④FDR：算法输出中定向错误的边的数量（和基准网络对比）/基准网络中边的数量。

⑤Time：运行每个点的平均时间，单位为秒（s）。

其中①、②、③、④表示算法的精度，⑤表示算法的时间效率。

3.3 比较算法

（1）PC 发现比较算法

①MMPC：基于拓扑的经典PC 发现算法。

②HTION_PC：基于拓扑的经典PC 发现算法。

③S2TMB_PC：本文提取了基于打分的马尔科夫毯S2TMB 算法中发现PC 集的过程，命名为S2TMBPC 算法。

（2）局部因果结构学习比较算法

①P_C：一种基于限制的代表性全局因果结构学习算法。

②MMHC：一种基于打分的代表性全局因果结构学习算法。

③PCD-by-PCD：已有的局部因果结构学习算法。

④CMB：已有的局部因果结构学习算法。

3.4 实验结果

（1）PC 发现比较算法实验结果

比较算法在样本数量为5 000 的每个数据集上运行10 次，然后取平均值，实验结果如表2 所示。

由表2 可以看出，SIAPC 算法与基于限制的方法（MMPC 算法和HTION_PC 算法）相比较，其时间效率很低，但是在精度方面有了很大的改进。与基于打分的方法（S2TMB_PC 算法）比较，在时间效率和精度方面，SIAPC 算法都取得了较好的效果。

（2）局部因果结构学习比较算法的实验结果

比较算法在样本数量为5 000 的每个数据集上运行10 次，然后取平均值，实验结果如表3 所示。

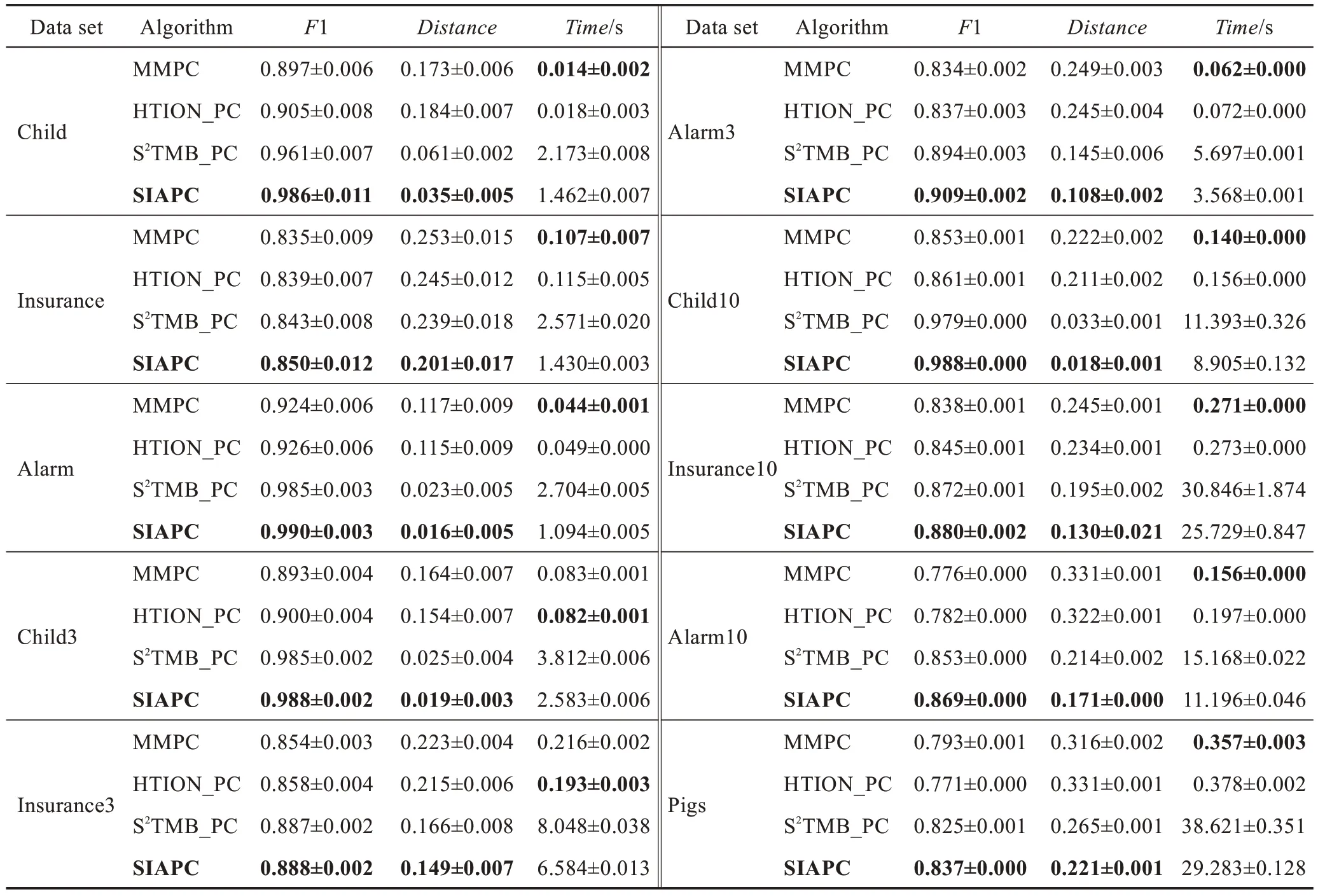
Table 2 Performance comparison of 4 PC discovery algorithms(size=5000）表2 4 种PC 发现算法的性能比较（size=5 000）

由表3 可以看出，算法HLCS 相较于已有算法，在精度方面有较大提升，但是在时间效率方面有相对较大的不足，但是因为本文主要针对的是局部因果结构算法的精度，对时间效率方面的改进将是下一步改进的内容。

HLCS 算法与全局因果结构学习算法（P_C 算法、MMHC 算法）相比较，在精度方面明显优于P_C算法和MMHC 算法很多，在时间方面也优于这两种算法。HLCS 算法与局部因果结构学习算法（PCDby-PCD 算法、CMB 算法）进行比较，在精度方面优于PCD-by-PCD 算法和CMB 算法，但是在时间效率方面有相对较大的不足。

3.5 数据量对局部因果结构学习算法的影响

本节说明当样本数据量不充分时，本文算法相对于已有的局部因果结构学习算法的比较情况。表4为在样本数量为500 时，算法的实验结果。而在表5中，将分析局部因果结构学习算法在数据量为5 000时的精度相较于数据量为500 时的精度的增长率，从而说明样本数据量的大小对算法的影响。

设定以下两个指标：

其中，RP表示算法在size=5 000 的数据量下ArrPrecision精度相对于在size=500 数据量下ArrPrecision精度的增长率；RC表示算法在size=5 000 的数据量下ArrRecall精度相对于在size=500 数据量下ArrRecall精度的增长率。表5 中的数据值越大，说明算法受数据量的影响越大。

从表4 可以看出，在数据相对不充分的条件下，HLCS 算法的精度相较于其他两个局部因果结构学习算法较好，但是时间效率相对不足。从表5 和图4中可以看出，随着数据集的增加，HLCS 算法的增长率最低，说明该算法可以有效缓减数据充分性。

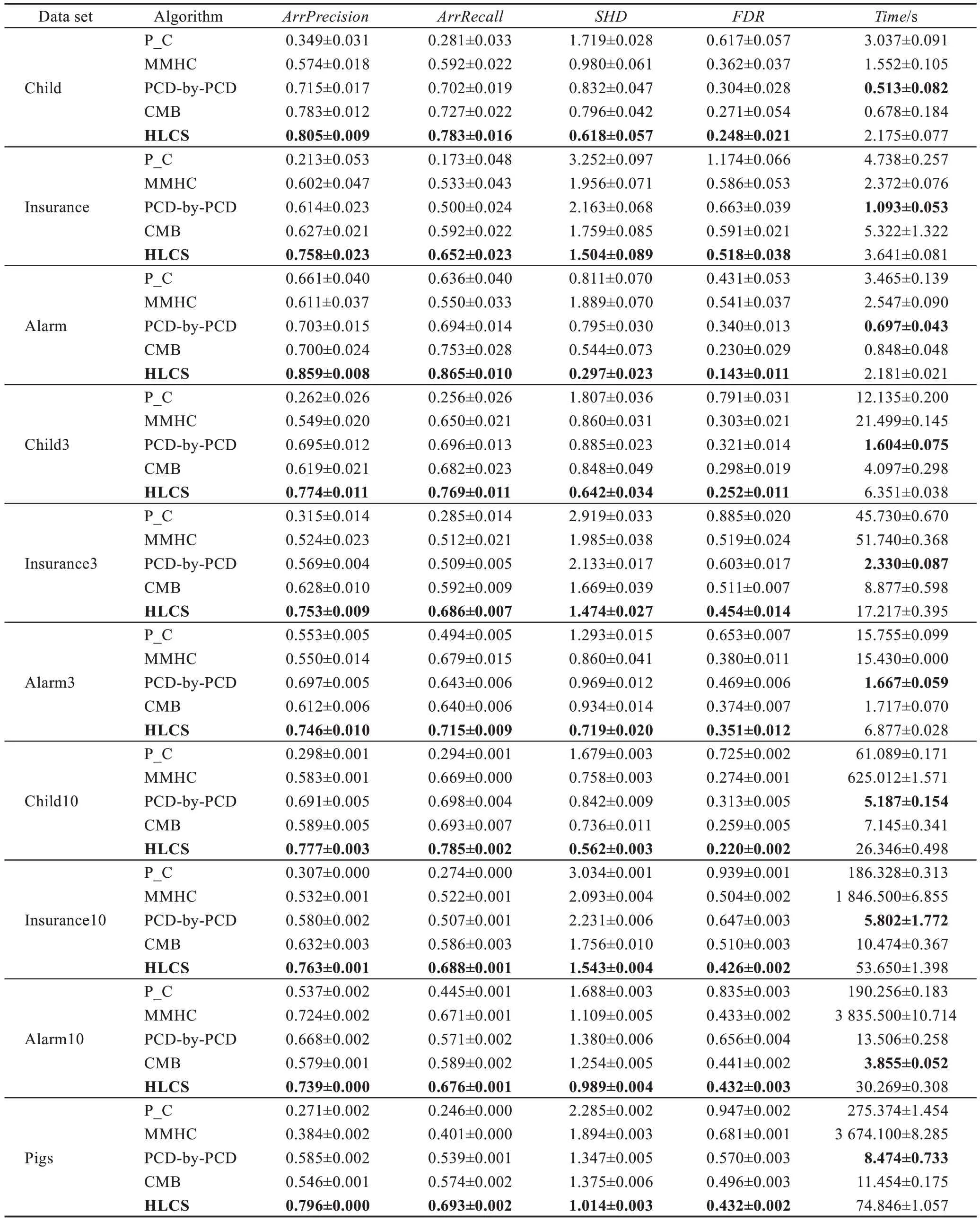
Table 3 Performance comparison of 5 local structure learning algorithms(size=5000)表3 5 种局部结构学习算法的性能比较（size=5 000）

Table 4 Performance comparison of 3 local structure learning algorithms(size=500)表4 3 种局部结构学习算法的性能比较（size=500)

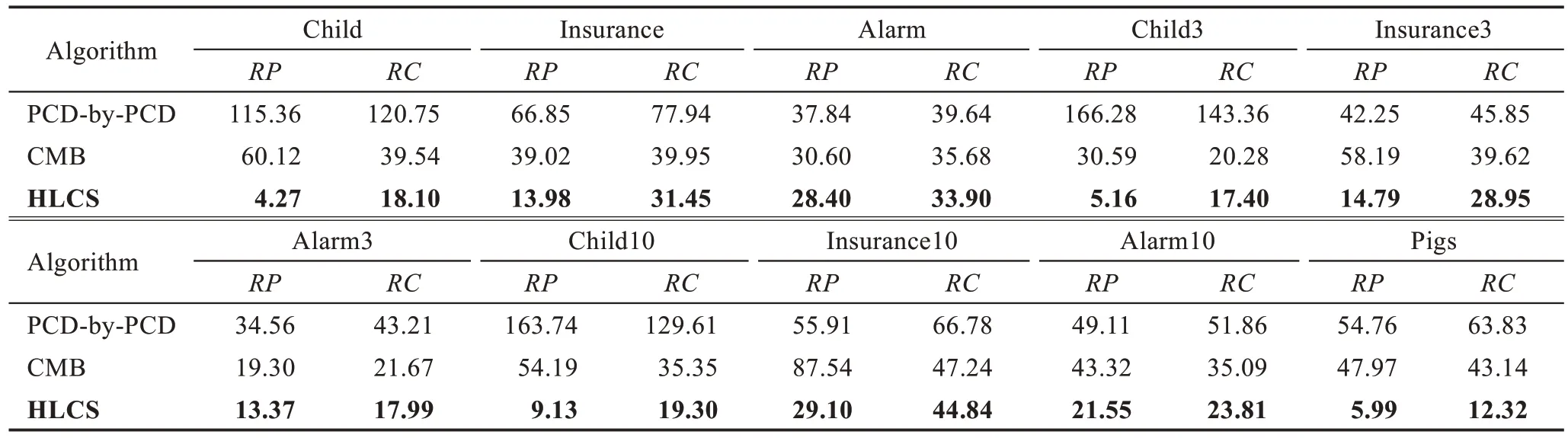
Table 5 Growth rate of accuracy of algorithms at size=5000 compared with size=500表5 算法在size=5 000 时对size=500 时精度的增长率 %

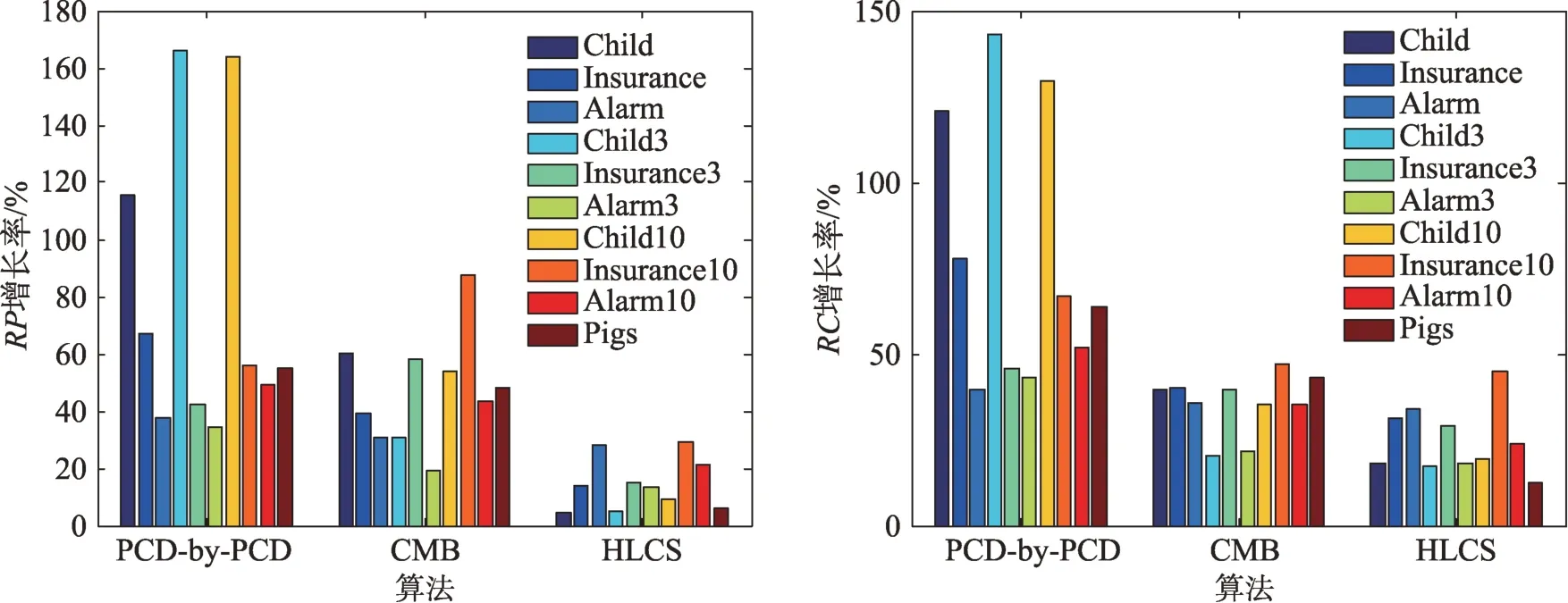
Fig.4 Growth rate of RP and RC of algorithm at size=5000 compared with size=500图4 算法在size=5 000 时对size=500 时RP和RC的增长率

4 结束语

本文针对已有算法的定向结果依赖目标变量的MB/PC，以及其结果取决于V 结构的发现的问题，提出一个基于打分和限制相结合的混合局部因果结构学习算法——HLCS 算法。该算法在步骤1 提出了基于打分和限制相结合的PC 发现算法，有效地提高算法精度；在步骤2 利用PC 发现算法得到的定向结果和对部分数据集打分得到的定向结果的交集来确定边的方向，然后使用条件独立测试进一步修正边的定向结果，该方法可有效降低对V 结构的依赖性。同时因为步骤1 和步骤2 都是结合基于打分的方法进行的，所以HLCS 算法可以有效缓减数据效率问题。实验验证，在标准假设下，本文算法相较于已有的算法在精度方面有较大的提高，但是由于打分方法的低效性，提高时间性能是下一步的研究工作。