UHPC-NC组合构件界面行为研究
2021-04-10欧阳娜邓舒文
欧阳娜,邓舒文
(1.江西省公路科研设计院, 南昌 330002;2.湖南大学 土木工程学院, 长沙 410082)
超高性能纤维增强混凝土(UHPC, ultra high performance concrete)是一种纤维增强型混凝土,主要由水泥、硅灰、钢纤维、水及高效减水剂等根据最大密实度理论配合而成。不同于常规混凝土材料,UHPC通常具有极低水灰比,极少或无粗骨料,内部掺杂高强钢制纤维等特征。UHPC材料根据内部钢纤维掺量不同,其抗压强度可达120~400 MPa,抗拉强度可达6~30 MPa[1]。其优异的力学性能引起工程界瞩目,随1997年第一座UHPC桥梁[2]在加拿大建造而成,UHPC的应用在世界上逐步推广[3-6],国内对UHPC的应用起步于2006年迁曹铁路线滦柏干渠大桥的20 m后张预应力桥梁[7],随后邵旭东教授提出使用UHPC材料增强钢桥面的应用在全国大范围推广,目前已用于多处钢结构桥梁的建设或加固[8-9]。
然而,由于UHPC内部掺加昂贵的钢纤维,其价格通常是普通混凝土的数十倍,因此,较为经济的方式是将UHPC材料应用于常规混凝土结构中重点受压或受拉部位,例如预制结构的节点接缝处。目前,国外研究者对UHPC接缝性能做了较多研究[10-14],国内的管亚萍等[15]对应用于与UHPC π型桥梁的纵向接缝进行了试验研究和理论分析;Pan等[16]提出适用于钢-RPC轻型组合桥梁结构的不同接缝构造形式;邵旭东等[17]对适用于钢-RPC轻型组合桥梁结构的RPC湿接头进行了不同配筋形式的弯曲试验;陈贝[18]对不同形式、不同配筋的UHPC接缝连接NC(normal concrete)面板进行了试验研究和理论分析。
高昂的研究经费促使了有限元软件的兴起,有限元计算现已成功应用于绝大多数工程设计、计算和实施中,目前对于常规结构的计算发展已十分成熟,但却鲜少见到关于接缝界面的接触模拟研究。接缝结构作为预制结构的节点,其强度几乎成为结构的控制因素,因此,对新兴材料UHPC加固传统混凝土进行有效的有限元计算拟合十分重要。笔者基于现有文献,总结试验结果和数据,并以其中一文试验数据为例,建立一个可以高度拟合UHPC-NC界面行为的3D有限元模型,以期为后来的计算提出可借鉴的拟合参数。
1 UHPC-NC界面粘结强度分析
对于新老混凝土界面粘结强度的理论分析主要基于两种常规混凝土的结合面,继Anderson[28]根据推出试件提出的界面抗剪强度公式后,Birkeland[29]提出了对其后研究产生深远影响的摩擦抗剪理论,该理论至今仍被各混凝土规范[30-34]作为理论基础,其理论计算式为
νn=μρfy,
(1)
式中:vn为截面抗剪强度;μ为界面摩擦系数;ρ为抗剪钢筋配筋率;fy为抗剪钢筋屈服强度。后来的研究均是基于上述摩擦抗剪理论计算式提出的线性或非线性计算式,同时部分学者[35]增加了界面粘聚力影响,式(1)基本形式变为
νn=τcoh+μ(ρfy+σn)。
(2)
上述规范中,除ACI规范[30]和PCI规范[33]仍保地仅计入混凝土界面的抗剪强度外,其余规范均采用了考虑粘聚力影响的式(2),以AASHTO规范[31]为例,其基本表达式为
(3)
式中:Acv为界面处混凝土面积;Acf为抗剪钢筋面积;c为粘聚力大小;μ为摩擦系数;fy为抗剪钢筋屈服强度;Pc为正交于抗剪界面的压力大小,若界面处受拉时,Pc为0。值得注意的是,式中c和μ的数值取决于破坏面所在位置,若破坏面位于基体中,则c和μ为基体的粘聚力和摩擦系数。同时AASHTO指出,对于不同的两种材料交界面,应根据试验结果决定c和μ的大小。目前,对于UHPC-NC界面c和μ的大小的试验研究中,粘聚力c主要通过拔出、劈裂、轴拉、弯拉试验等确定;摩擦系数μ则主要通过斜剪、直剪试验等确定,试验方法示意如图1所示。
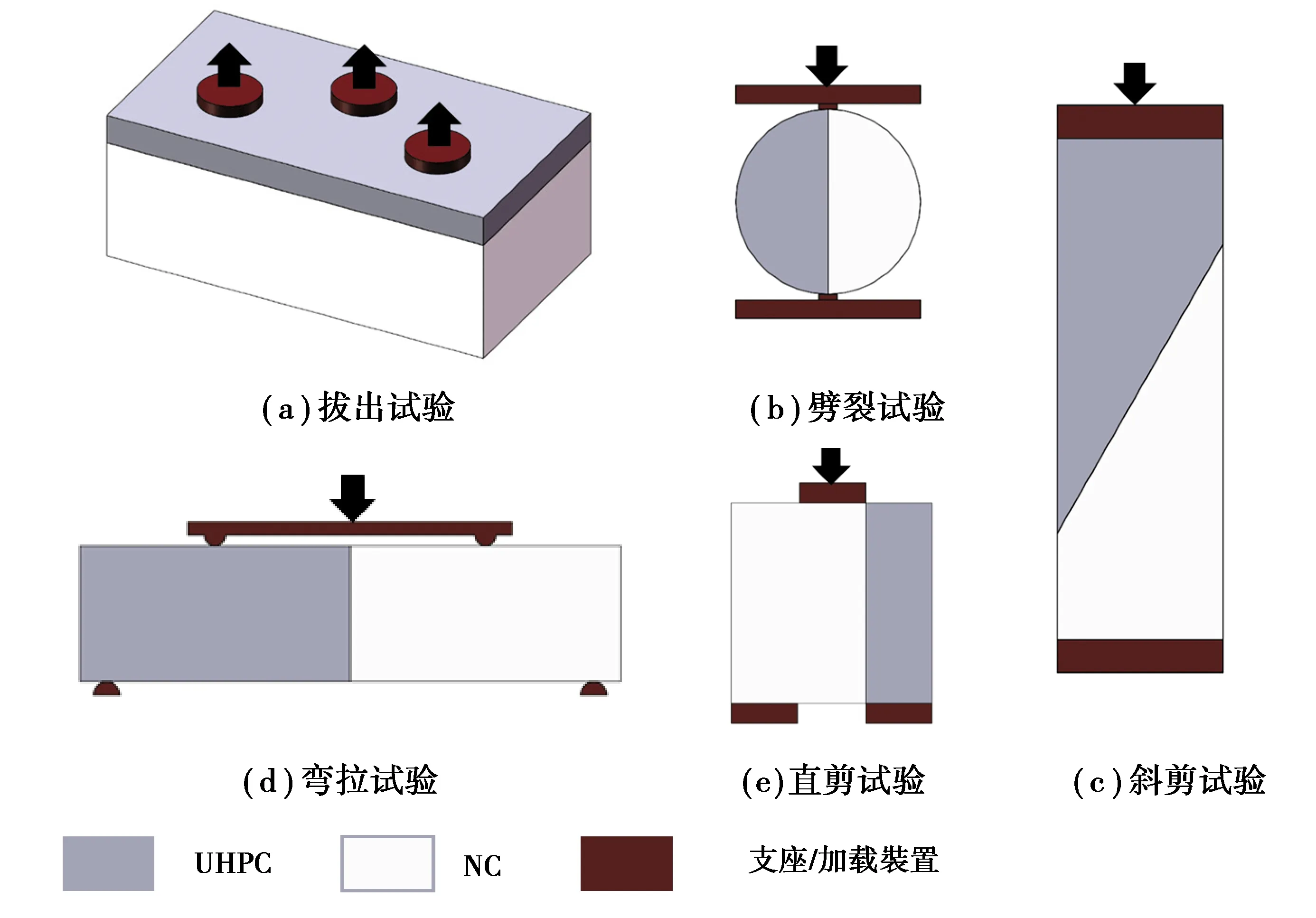
图1 试验方法示意图Fig. 1 Schematics of test method
1.1 粘聚力c的确定
过往文献中先后浇注或不同材料组合试件的试验结果基本表现为3种破坏模式,即破坏于较弱基体、破坏于界面及较强基体损坏。对于UHPC-NC界面,绝大多数破坏发生于NC基体上,同时Carbonell[19]指出劈裂试验获得的粘聚力大小大于拔出试验。对于拔出试验和轴拉试验,使用式(4)来计算粘聚力大小。
(4)
式中:T为拉伸破坏强度;P为最大施加荷载;A为接触界面的混凝土面积。对于劈裂试验,劈裂强度的计算式为
(5)
式中:Ts为试件劈裂强度;P和A意义同上。对于弯拉试验,其粘结强度的计算式为
(6)
式中:L为试件跨径;b为试件截面宽度;d为试件截面高度,其余同上。对上述文献中粘聚力大小、试验方式及破坏模式进行汇总,如表1所示。

表1 粘聚力大小及破坏模式汇总Table 1 Summery of cohesive strength and failure modes
由表1可见,相同测试类型时,不同测试方法得到的粘聚力分别为2.18~2.92 MPa(拔出/轴拉),2.77~5 MPa(劈裂试验),2.8 MPa(弯拉试验)。与文献[19]所述一致,劈裂试验得到的结果普遍大于直接拉伸试验,而弯拉试验则介于二者之间。不同粗糙程度界面的拔出/轴拉试验得到的粘聚力分别为2.24 MPa(光滑界面),2.37 MPa(中等粗糙界面),2.66 MPa(粗糙界面)。对于粗糙界面,其破坏位置均位于NC基体内,因此,此时得到的粘结强度也应为NC基体的拉伸强度,而不是界面的粘结强度。
1.2 摩擦系数μ的确定
与粘聚力一样,摩擦系数的确定也同样分为3种破坏形式及3种界面形式,通常采用斜剪试验经过倒推确定。法向应力和切向应力及摩擦系数可根据摩尔库伦定理(图2)及式(7)~式(9)确定。
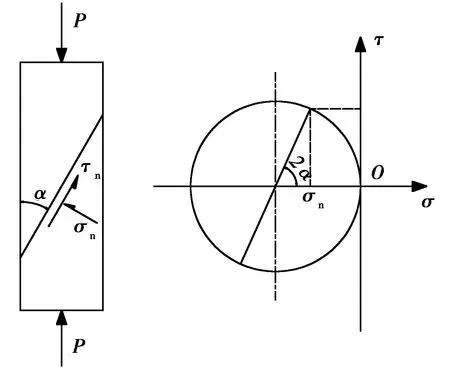
图2 斜剪试件计算和摩尔库伦圆Fig. 2 Slant shear stress calculation and Mohr-Coulomb circle
(7)
(8)
τn=c+μσn,
(9)
式中:σn为界面处的法向应力;τn为界面处切向应力;α为界面斜交角;A为加载处截面面积,其余符号同上。对文中提及文献得到的正应力、法向应力及摩擦系数汇总如表2所示。
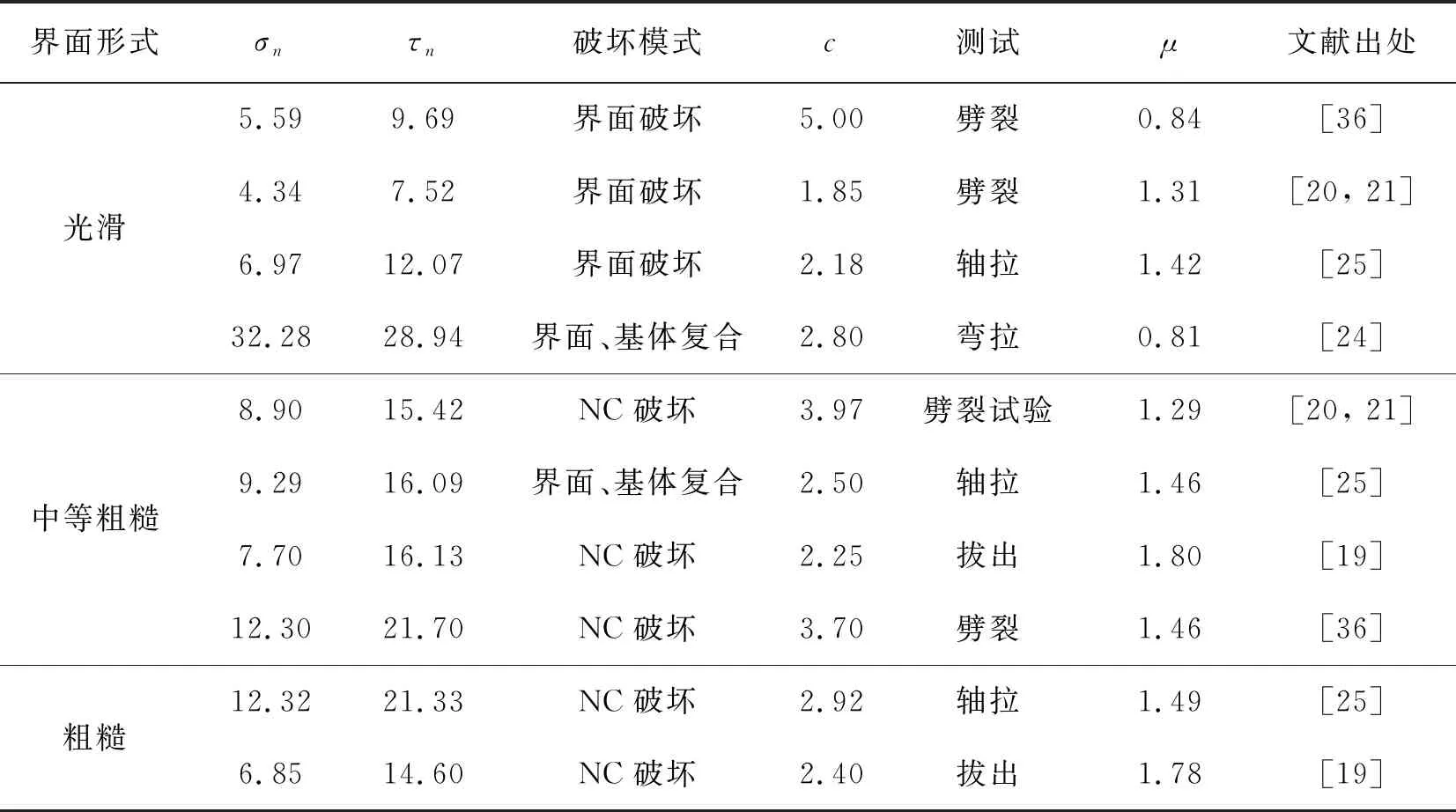
表2 摩擦系数及破坏模式汇总表Table 2 Summery of friction coefficient and failure modes
由表2可见,直接拉伸试验(轴拉/拔出)得到摩擦系数普遍大于劈裂或弯拉,3种界面摩擦系数均值分别为1.42,1.63和1.64。同样,粗糙界面和部分中等粗糙界面的破坏发生于NC基体处,因此,此时得到的数值为NC基体的摩擦系数,而非界面处的。
至此,可根据上述试验结果得到基于AASHTO规范的3种界面形式的粘结强度分别为
(10)
2 有限元模型参数拟合
目前工程中多使用有限元方法预测结构承受荷载后的响应,而对于先后浇注或不同材料之间的界面行为的模拟却没有统一的方式。以ABAQUS软件为例,ABAQUS中提供多种模拟界面行为的选项,例如,部分学者使用完全粘结(tie)对界面行为进行简化[37-39];还有学者假设界面间存在一种粘结材料[24, 40],通过试验拟合得到界面材料的参数;部分学者仅在界面间设置摩擦系数[41-42];Dias-da-Costa等[43]设置一种零厚度的线性接触单元模拟结合面。

上述方法中,完全连接为界面连接的一个上限状态,根据表1和表2的试验结果,当界面形式为粗糙时,破坏发生于NC基体,此时可假设界面完全连接;当界面形式为中等粗糙和光滑时,使用完全粘结会过高地估计试件的承载力而得到一个错误的结论。当仅设置摩擦系数时,即与式(1)一致,计算仅计入了界面间摩擦系数的影响,而忽略了界面间粘聚力的影响,大量的试验结果已经证明了粘结力的存在,即使是光滑界面,粘结力也不容忽视,因此,仅考虑摩擦系数时会过小地估计试件承载力。Chen[45]采用默认系数的硬接触和切向摩擦系数相结合的方式,但此接触设置并未考虑界面形式。根据上文众多试验结果可见,光滑、中等粗糙和特别粗糙界面之间的粘聚力和摩擦系数均是不相同的,因此,此方法并不具有通用性;Steinberg等[45]采用的方法设置了较多参数,但结果却差强人意。
设置界面粘结材料是一种较为理想的方法,可通过试验获得界面材料的参数,Shafieifar[24]通过弯拉、直接剪切及斜剪试验获得了UHPC-NC组合试件界面材料的弹性模量、泊松比及CDP(concrete damage plastic)相关参数,并设置界面厚度为100 μm,但并未对此数值做出进一步解释。韩菊红等[48-49]通过对新老混凝土粘结面破坏模式的研究中,也提出类似的结论,并将此界面层定义为“断裂过程区”,通过试验与理论分析得到断裂过程区长度为
(11)
式中,KIc为粘结断裂韧度,f′t为界面层抗拉强度,二者皆为界面材料的特性,需要通过试验确定,根据韩菊红[48]的研究,新老混凝土之间的断裂过程区长度为26.4 mm,这个结果与Shafieifar[24]相差巨大,且当接缝界面为异形时(例如锯齿形、燕尾型等),单独建立界面层难度较大。

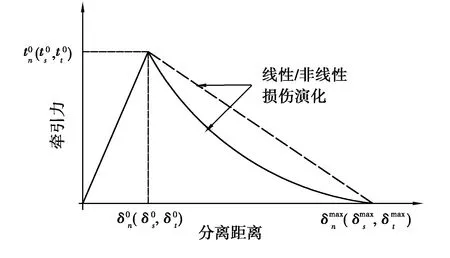
图3 接触分离模型Fig. 3 Typical traction-separation response
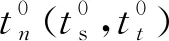
(12)
式中,K为弹性阶段的接触刚度矩阵,同样包含3个方向。当粘聚力达到峰值点(即图3中的t0)时,损伤开始发生。后期的损伤演化段可表述为线性或非线性形式,值得注意的是,这里的损伤是指接触属性中的损伤,而非材料特性值。ABAQUS中对接触损伤准则的定义分为4种:最大应力准则,最大分离准则,二次应力准则和二次分离准则,其中最大应力准则形式简单,定义明确,为
(13)
即当任意方向的粘聚力达到设置的最大应力时,损伤开始发生。图3中损伤退化的部分可用线性或非线性形式表示,ABAQUS中使用D表示接触点的损伤,该变量由0增至1,表示损伤开始发生直至完全损伤,其计算式为
(14)
为了表示3个方向总的分离值,引入δm,其计算式为
(15)
而当损伤阶段设定为线性时,损伤D可表示为
(16)
当损伤段定义为非线性时,损伤D可表示为
(17)

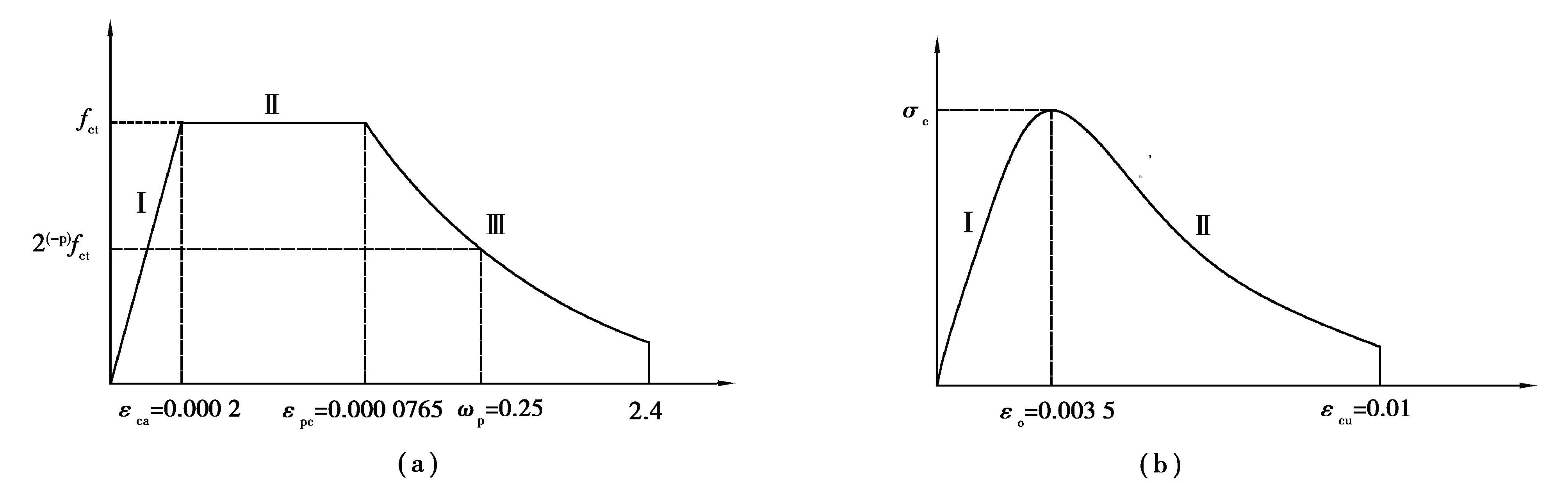
图4 UHPC应力应变关系Fig. 4 Stain-stress relationship of UHPC
混凝土损伤塑性模型中除定义材料本构关系外,还需确定与塑性准则等相关的参数,这些参数参考文献[9]选取,即膨胀角为36°,偏心系数为0.1,双轴抗压强度与单轴抗压强度之比为1.16,K为0.667,粘性系数为0。
2.1 拉伸构件拟合参数确定
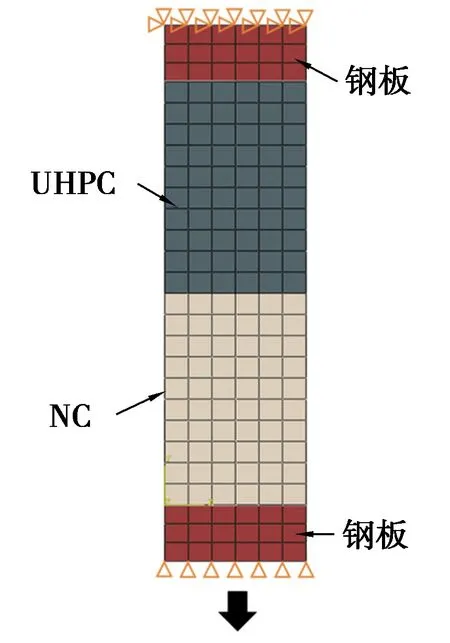
图5 拉伸构件有限元 计算图示Fig. 5 FEM work for tensile test
以文献[25]中轴拉试验为基准对试验结果进行拟合以确定拉伸构件的拟合参数。文献中,光滑界面破坏荷载均值为21.80 kN,钢刷界面(中等粗糙)为24.98 kN,二者的破坏模式均为界面失效结合NC部分脱落,凿毛界面(粗糙)破坏荷载均值为29.16 kN,破坏模式为NC破坏。有限元模型如图5所示,模型采用C3D8R八节点三维实体单元建立,试验中未见钢板与混凝土脱粘现象,钢板和混凝土采用完全粘结,试验机为下部向下牵引,因此,模型中也采用拉伸下部结构的加载方式。
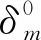
当材料由弹性转为塑性时,对应一个弹性极限应变,此时也是结构损伤的起点,此时弹性极限应变为
(18)
又由应变的定义可知,应变为某一方向上微小线段因变形产生的长度增量与原长度的比值,当标距一定时,可得到长度增量为
Δl=εl。
(19)
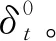
根据接触分离模型(图3)可知,弹性阶段接触刚度可由式(12)得到。至此,凿毛界面的参数全部获得,由Hussein[46]的试验结果可见,界面粗糙度不同时,轴拉试件荷载位移曲线的刚度相差不大,因此,其他两种界面参数可参考凿毛界面参数略微调整后得到,3种界面的拟合参数和结果见表3,该参数适用于受拉为主的构件界面。
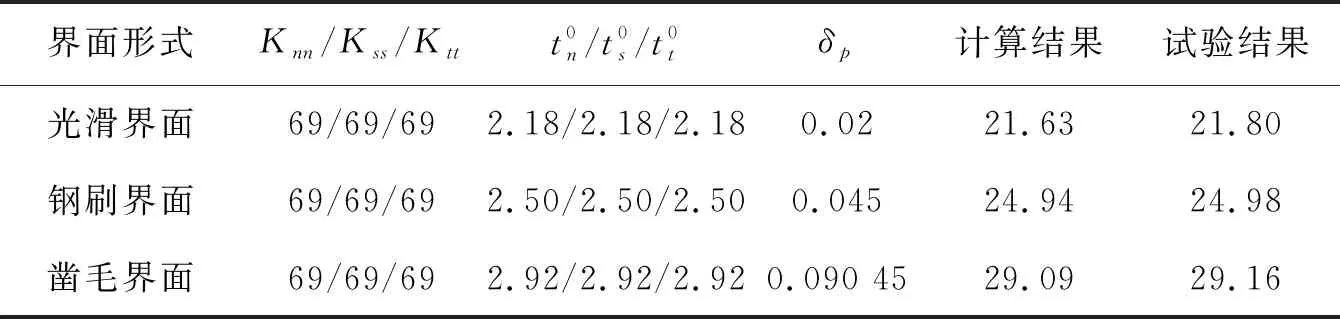
表3 受拉为主构件界面拟合参数Table 3 Interface fitting parameters of tension-dominated components
2.2 压剪构件参数确定
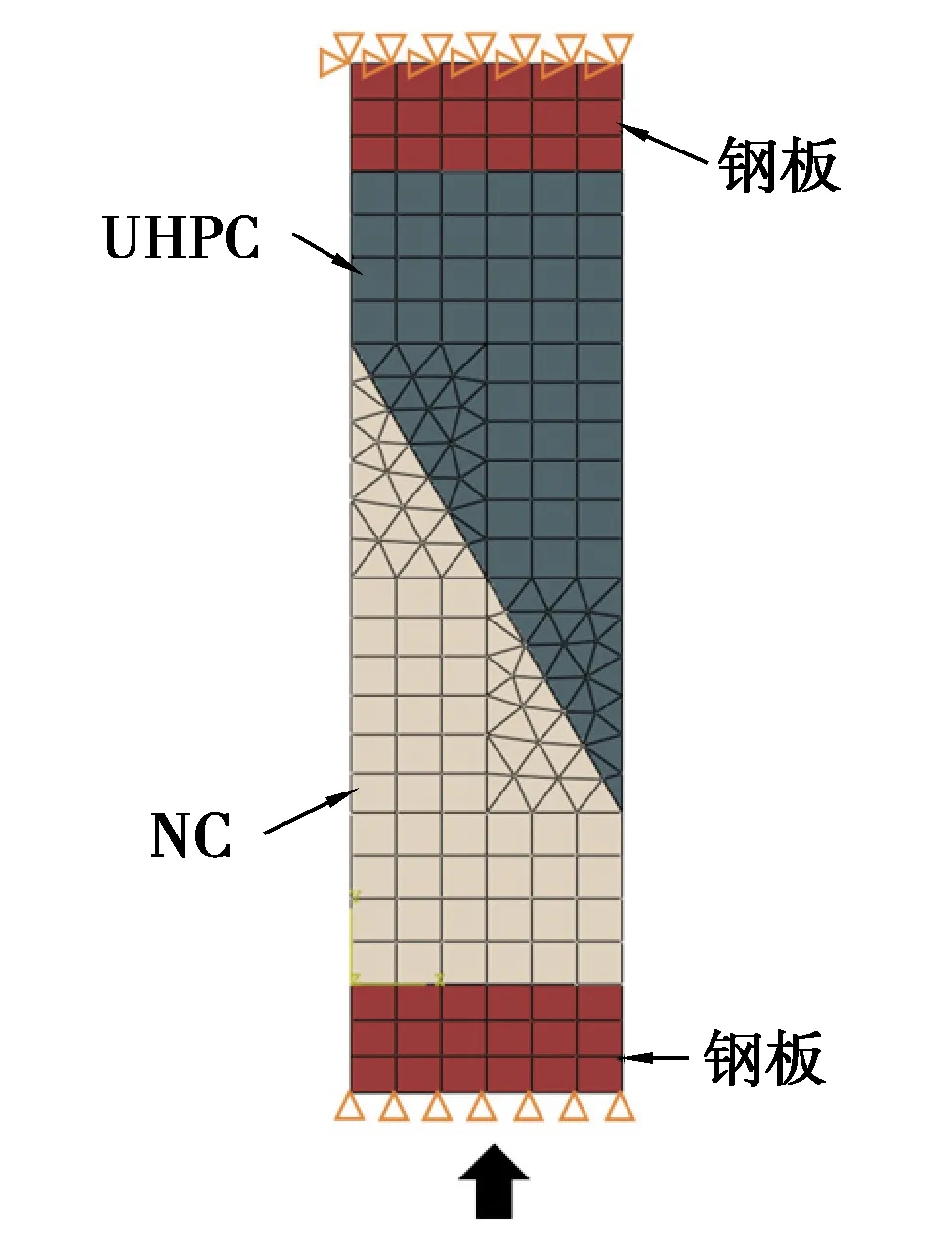
图6 斜剪构件有限元计算图示Fig. 6 FEM work for slant shear test
压剪构件参数的确定参考文献[25]中斜剪试件的试验结果。模型(图6)中接触参数除定义与粘聚力、损伤相关参数外,还需定义界面间摩擦系数。试件加载初期,剪力沿界面传递,此时粘聚力模型激活,由粘聚力对抗逐渐增大的剪切滑移;加载后期随荷载逐渐增大,粘聚力达到峰值,接触损伤激活,粘聚力模型对抵抗剪力的贡献逐渐降低,此时摩擦系数被激活[46]。根据文献[25]所述,3种界面对应峰值荷载分别为278.68 kN、371.70 kN及492.71 kN,经式(7)~式(9)计算得到表2中所示的法向应力和切向应力及摩擦系数。其中法向和切向应力分别对应3个方向的最大分离应力,同样地,凿毛试件破坏位于NC基体,则其接触刚度、初始分离距离等参数可通过材料性能计算并小幅调整得到。最终模型参数和拟合结果如表4所示,该参数适用于受压剪为主的构件界面。
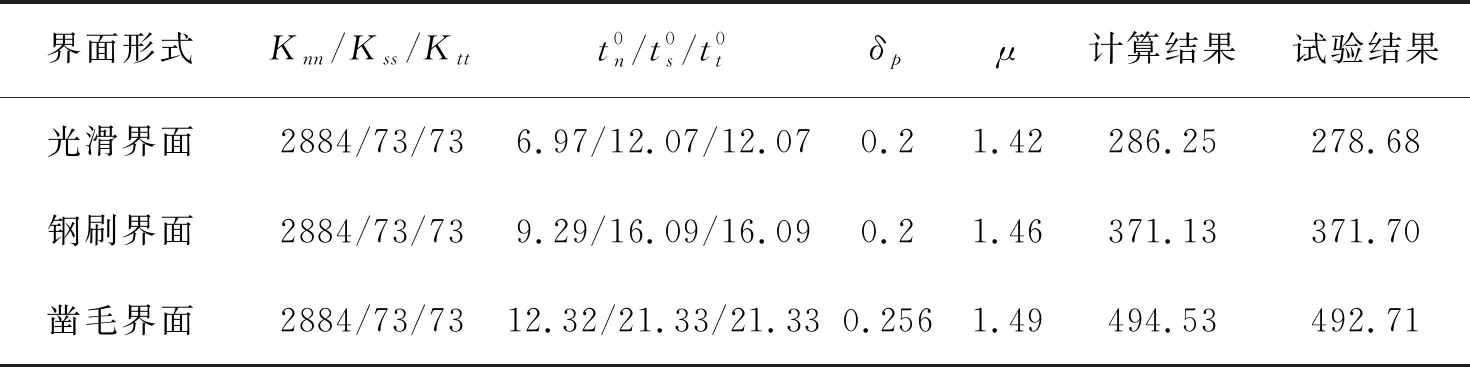
表4 受压剪为主构件界面拟合参数Table 4 Interface fitting parameters of compression and shear dominated components
2.3 有限元参数有效性验证
为验证有限元参数的有效性,建立部分文献试验的有限元模型,将相应参数带入比较,结果如图7所示。由图可见,部分拟合结果因材料参数不完备等因素而存在较大偏差,但总体较为吻合,具备一定参考性。

图7 文献试验值与有限元计算值对比Fig. 7 Comparison between test value and FEM work
3 结 论

1) 不同粗糙程度界面经直接拉伸试验得到的粘聚力分别为2.24 MPa(光滑界面),2.37 MPa(中等粗糙界面),2.66 MPa(粗糙界面);
2) 直接拉伸试验得到摩擦系数普遍大于劈裂或弯拉,3种界面摩擦系数均值分别为1.42,1.63和1.64;
3) 劈裂试验得到粘聚力的结果普遍大于直接拉伸试验,而弯拉试验得到的结果则介于二者之间,经直接拉伸试验数据计算得到摩擦系数普遍大于劈裂或弯拉试验;
4) 针对3种粗糙度不同界面提出基于粘聚力和抗剪强度的UHPC-NC界面强度计算式;
