美国水工混凝土规范压弯构件正截面承载力计算
2021-04-09董正中陈天恩
董正中,陈天恩,李 贺
(中国电建集团西北勘测设计研究院有限公司,西安 710065)
0 前 言
随着中国越来越多的参与国际水电工程建设,需要我们对国外尤其是美国规范有更深入的理解。水电工程中的偏心受压构件多出现在结构柱、水工衬砌结构受外水压力时的截面之中。本文在采用美国规范进行水电工程偏压构件正截面承载能力计算时,主要参考了美国ACI 318M-14[1]《混凝土结构设计规范》(简称ACI)和EM 1110-2-2104[2]《水工钢筋混凝土结构强度设计规范》(简称EM)2本规范。
在查阅规范中发现,ACI对混凝土截面设计虽然做了一些原则性的规定与假设,但需要设计者在满足ACI 规定情况下选用适宜的计算方法。而EM 规范针对水工结构做了一些补充原则,且在EM附录B中给出了偏压正截面承载力计算公式,但附录B限于篇幅,个别公式有疏漏之处,未把各种情况下的计算公式描述全面。笔者查阅了一些关于水工偏压构件正截面承载力计算教程,发现大部分采用手动计算判别,比如截面受拉还是受压控制,受压钢筋是否屈服等。本文在梳理的EM附录B公式的基础上,补充相关计算公式,提出了适宜的压弯构件正截面承载力计算方法,提高设计工作效率。
1 计算原则与假定
(1) 混凝土最外边缘受压纤维处极限压应变εc等于0.003。
(2) 钢筋应力(受拉钢筋应力记为fs,受压钢筋应力记为fs′)若小于fy,则应取为钢筋应变(受拉钢筋应变记为εs,受压钢筋应变记为εs′)的Es倍。当钢筋应变大于与fy对应的应变εy时,钢筋应力应考虑与应变无关并等于fy。
(3) 平截面假定,应变沿截面高度呈线性变化。
(4) 当截面中受拉钢筋达到fy对应的应变时,若受压混凝土达到极限压应变0.003,截面存在临界平衡条件。当受压混凝土达到极限压应变0.003时,若εs≤εy,则截面由受压控制,若εs>εy,则截面由受拉控制。
(5) 假定存在数值为0.85fc′的混凝土等效受压区(应力均匀分布),该区域由横截面的边缘线和一条与中和轴平行并与极限压应变距离为a=β1c的直线所限定,如图2所示。β1的计算公式如下(fc′为混凝土抗压强度):
(1)
(6) 强度折减系数φ和受拉钢筋的应变εs相关[1],其表达式如下。具体说明见本文4.1节。
(2)
(7) 受拉钢筋的最大配筋率ρmax:建议限值为ρmax=0.25ρb[2],超过此值将要求考虑适用性、可构造性和经济性。ρb为当截面达到临界平衡条件时的受拉钢筋配筋率。其计算方法和相关说明见本文4.2节。
2 计算简图及通项公式
2.1 符号说明
Pn和Mn为名义强度或者标称强度;φPn和φMn为设计强度;Pu和Mu为计算得到的轴力和弯矩;ku为相对受压区高度;kb为临界平衡状态下相对受压区高度。
2.2 计算简图
公式(3)~公式(19)相关参数的意义见图1~ 4。
2.3 通项公式
(1) 截面压力Pu到受拉钢筋的偏心距:
(3)
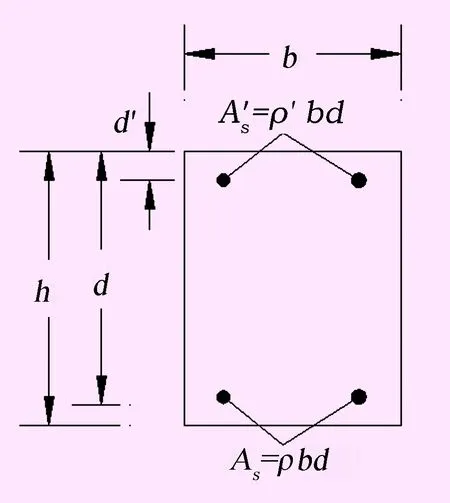
图1 截面尺寸及钢筋位置图

图2 截面受力简图
(2) 根据临界平衡状态下应变相似三角形(见图3),联立:
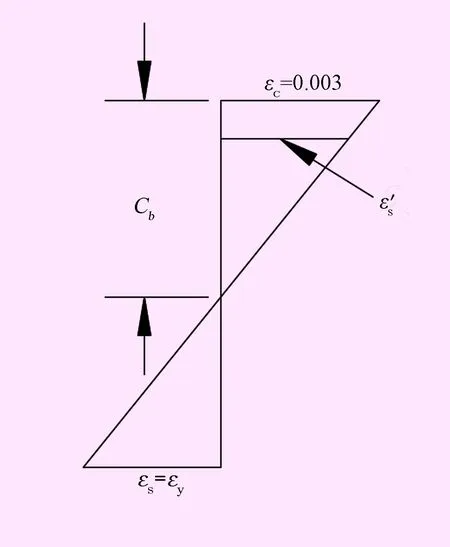
图3 临界平衡应变三角形图
(4)
(3) 截面力的平衡即可推出:
(5)
(4) 截面所有力对受拉钢筋的力矩求和即可推出:
(6)
(5) 由Pne′=Mn得出:
(7)
(6) 公式Mn/Pn即得出截面压力Pn到受拉钢筋的偏心距:
(8)
公式(5)~(8)即为偏心受压正截面承载力计算的通项公式。
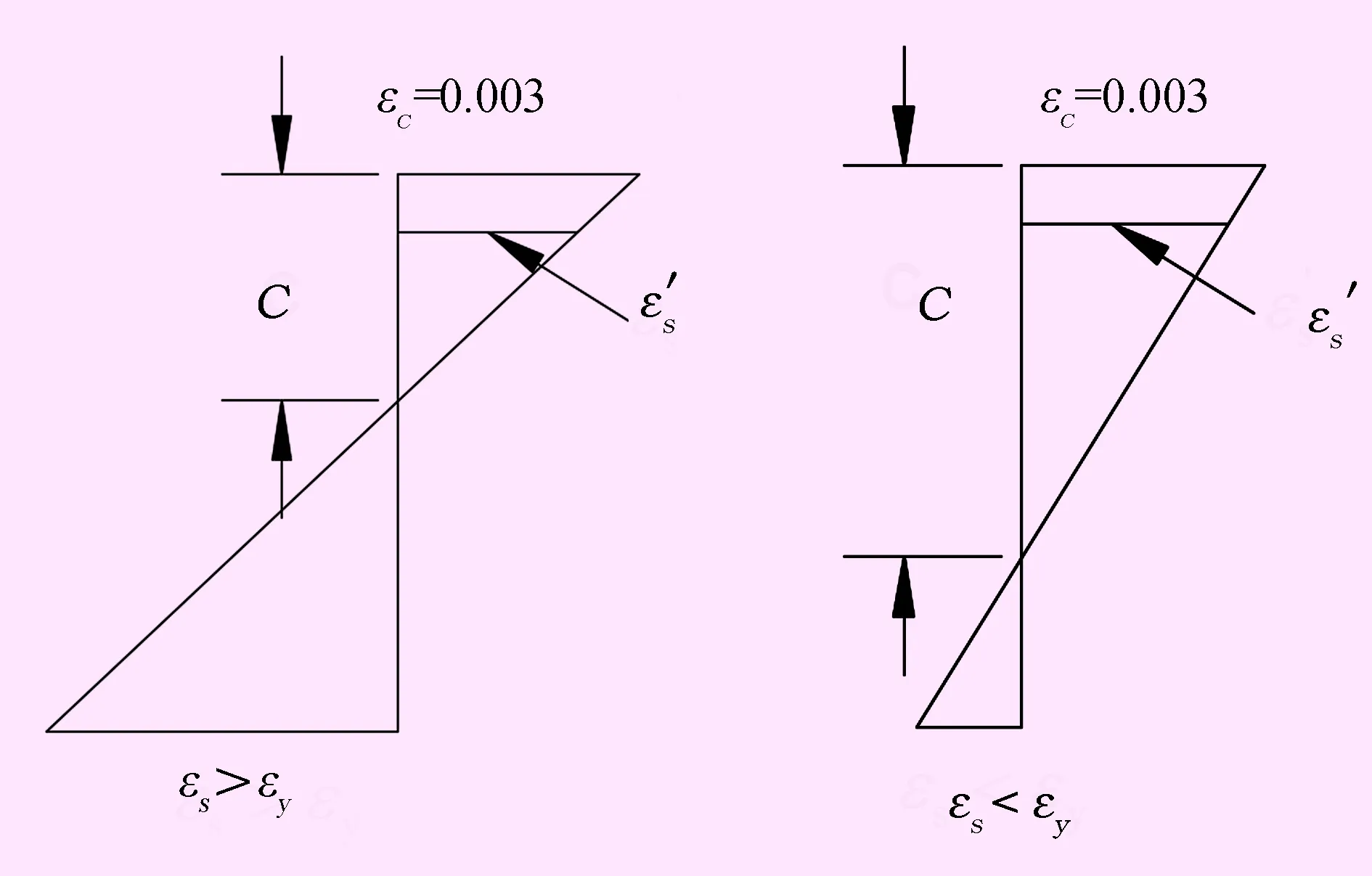
图4 受拉/压控制应变三角形图
3 计算过程
本文将按先按单侧(受拉侧)配筋求解ρ,若单侧配筋无法得出ρ,再按双侧配筋求解ρ和ρ′。无论是单侧还是双侧配筋,在计算前根据ACI规范,Pn需按下面公式进行轴力判断,若不满足则需调整截面尺寸。
φPn(max)=0.8φ[0.85fc′(Ag-(ρ+ρ′)bd)+fy(ρ+ρ′)bd]
(9)
3.1 单侧配筋
令ρ′=0以及ρ在0~ρmax之间搜索;对于每个ρ,先求解临界平衡条件下的eb(公式8);若e′≥eb则按单侧受拉控制,若e′ 3.1.1单侧配筋临界平衡的eb 令ρ′=0,ku=kb,fs=fy,代入公式(8)即可求出临界平衡下的偏心距eb。 3.1.2单侧配筋受拉控制 令ρ′=0,fs=fy,代入公式(7)整理如下,计算时需剔除小于0的根。 (10) 3.1.3单侧配筋受压控制 先假设fs>-fy,则根据应变三角形(见图4),利用混凝土极限压应变εc侧的相似三角形,很容易推出: (11) 将公式(11)和ρ′=0代入公式(7)如下,此方程为ku的一元三次方程,本文采用盛金公式[3]求解,计算中不需要迭代求解,可根据判别式直接求出根,但需剔除掉复数根和小于0的根。 (12) 求出ku后需代回公式(11)看是否fs>-fy。若是,则ku即为所求;若不是,则令fs=-fy以及ρ′=0重新代入公式(7)来求解ku,整理如下: (13) 3.2.1双侧配筋临界平衡的eb 临界平衡条件下,根据应变三角形(见图3),利用混凝土极限压应变εc侧的相似三角形推出: (14) 将公式(14),ku=kb,fs=fy,代入公式(8)即可求出临界平衡下的偏心距eb。 3.2.2双侧配筋受拉控制 先假定fs′≤fy,则根据应变三角形(见图4),利用混凝土极限压应变εc侧的相似三角形(EM规范B-31在此情况下利用受拉钢筋εy侧的相似三角形来推导fs′,本文觉得不妥,在此情况下受拉钢筋εs已大于εy,所以不该用εy推导而应该用εc推导),很容易推出: (15) 将公式(15)以及fs=fy代入公式(7)整理如下: (16) 求出ku后代回公式(15)判断是否fs′≤fy。若是,ku即为所求;若否,则令fs′=fy以及fs=fy重新代入公式(7)来求解ku,整理如下: (17) 3.2.3双侧配筋受压控制 先假设fs′≤fy,则根据应变三角形(见图4),利用混凝土极限压应变εc侧的相似三角形(见图4),推出fs和fs′分别为公式(11)和公式(15),将公式(11)和公式(15)代入公式(7)整理如下: (18) 求出ku后需代回公式(15)判断是否fs′≤fy。若是,则ku即为所求;若否,则将公式(11)以及fs′=fy重新代入公式(7)来求解ku,整理如下: (19) 若搜索完毕仍找不出满足0≤(φPn-Pu)/Pu≤0.01条件的ρ或者ρ和ρ′,则看所有搜索的ρ和ρ′求出的φPn的最大值。假如最大值仍比Pu小,则说明截面尺寸不够,需增大,否则说明截面不需要配筋(此处的不需要配筋仅从平衡方程角度来说,实际仍需考虑构造要求)。 根据φ的定义,第1种最直接的方式求解φ即为在求出满足要求的ku后,再根据应变三角形求出εs,然后按定义求解。但是计算的第一步是轴力判断公式(9),此时并不知道φ的值,若将轴力判断放在求解ku之后会带来一些不必要的计算。 本文采用第2种方法,经过观察试算,截面压力Pn到受拉钢筋的偏心距e′公式(8)与εs近似线性相关。因此,可以利用e′公式(8)来线性插值求解φ。具体计算方法和本文3.1.1以及3.2.1求解eb的方法类似,即在计算公式(4)的kb时,分别令εy=fy/Es和0.005,求出2个kb(kb1和kb2),用kb1和kb2分别可以求出eb1和eb2,用公式(3)的e′在eb1和eb2之间插值即可求出φ。 根据单侧配筋临界平衡时的应变相似三角形,以及轴力平衡,推出 : (20) 以及类似可以求出双侧配筋临界平衡受拉钢筋配筋率: (21) 当按单侧配筋搜索时,ρ在0~0.25ρb1之间变化;当按双侧配筋搜索时,ρ′在0~0.25ρb1之间变化,同时ρ在0~0.25ρb2之间变化。 某截面尺寸及钢筋混凝土强度如表1。 表1 截面参数表 截面在几种典型内力组合下的配筋如表2。 表2 典型内力组合下配筋量表 从计算结果看出,首先保持Pu为一极小的值,在逐渐增大Mu过程中,单侧受拉钢筋面积一直增大至变成双侧配筋,这一过程即为纯弯正截面承载力计算过程,若再增大Mu,则截面尺寸不够。此时保持Mu不变,逐渐增大Pu,截面由双侧受拉控制——单侧受拉控制——单侧受压控制——双侧受压控制,与实际规律相符。将每种组合下的结果代入平衡方程公式(7)验算,发现等式成立。 若已知截面尺寸和钢筋配筋面积,要求核算截面所能承受内力,则相对容易,根据钢筋面积判断拉/压控制,然后代入平衡方程求解ku,进而求出φPn。 (1) EM计算压弯构件时,先按单侧配筋计算;单侧无法满足再按双侧配筋考虑,配筋时实际满足要求的ρ和ρ′组合可能不止一个。本文选取的附加条件是满足ρ′最小,比如:DL/T 5057-2009《水工混凝土结构设计规范》选取的附加条件是ρ+ρ′最小或者ρ=ρ′等[4],计算中可结合不同工况受力的分析以及工程需要选择合适的附加条件。 (2) 按照平衡方程计算ρ和ρ′,实际配筋时需考虑最小配筋率等相关构造要求。 (3) EM规范与DL/T 5057-2009《水工混凝土结构设计规范》在原则假定以及平衡方程基本相通,但在细节处理上有所不一致。如我国大偏压截面为保证受压钢筋屈服需满足x≥2a′[5],而EM则无此要求,若实际钢筋强度很高时,加入x≥2a′的条件会影响配筋经济。3.2 双侧配筋

3.3 搜索失败
4 两个参数
4.1 强度折减系数
4.2 临界平衡受拉钢筋配筋率ρb

5 计算实例


6 结 语
