基于重点域的自适应加点方法

毛 勇，曾 锋，罗 曼

(武汉船舶通信研究所 武汉 430079)

复杂电子装备通常涉及到机械、电磁、热等多个学科，利用仿真软件进行计算时，需要在多个学科间进行多次迭代，导致整体计算量偏大，计算效率低下。为减少仿真的计算量，提高计算效率，引入代理模型是必然的选择[1]。多项式响应面、Kriging、径向基函数、支持向量回归等是常用的代理模型近似算法[2-3]。在实际应用中，利用Kriging模型进行设计的越来越多[4]。

通过加点方法不断更新代理模型是提高代理模型预测精度的一种重要手段。文献[5]提出的有效全局优化(efficient global optimization, EGO)算法是一种研究早且应用相对广泛的加点方法。文献[6]介绍了一种通过构造概率密度函数来选取新增样本点的径向基函数的追峰采样(mode pursuing sampling,MPS)方法，该方法在进行高维问题优化时计算效率较低。文献[7]提出一种集成最小化置信下限和信赖域(integrating minimize lower confidence bound and trust region, IMLCB-TR)的动态代理模型优化策略，该优化策略不仅能够保证最优解精度，优化效率也有一定程度的提高。文献[8]提出的一种基于智能空间探索的自适应响应面方法，该方法能够在一定程度上提高计算效率，但是该方法的近似能力不理想，导致其在实际应用中可能陷入局部最优。

针对上述问题，本文提出了基于重点域的自适应加点方法(adaptive infilling method based on significant domain)。该方法在每次迭代时通过建立局部加点和全局加点模型以分别提高代理模型的局部开发能力和总体探索能力。最后，将本文提出的方法应用于标准数学测试问题和某共形天线的优化设计中，从数值结果上验证本文方法的高效性和有效性。

1 基于重点域的自适应加点方法

基于重点域的自适应加点方法的基本思想为：利用空间缩放技术确定重点域，然后基于重点域建立局部加点模型以提高近似方法的局部开发能力，同时利用平衡变量和设计点的预测方差建立全局加点模型，提高近似方法的总体探索能力。

1.1 局部加点模型

为了提高近似方法的局部开发能力，在重点域的基础上，本文提出了一种局部加点方法，数学模型如下：

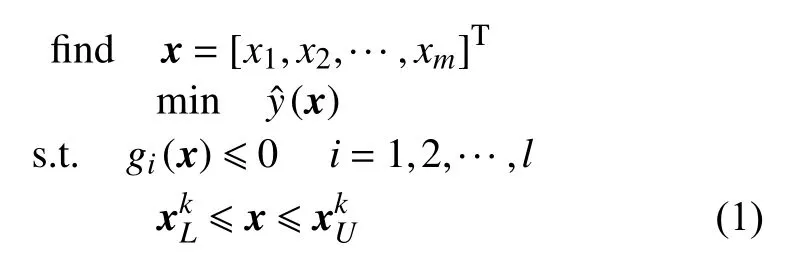
式中，中心点的更新方法如下：

取样范围的长度更新方法为：

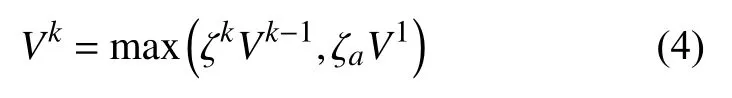
式中，Vk-1为第k-1次迭代得到的取样范围的长度值； V1为初始设计区间的长度。在迭代时，有可能会出现重点域长度过小而出现新增样本点在某一区域过于集中的问题，因此可给定最小重点域的长度ζaV1，参数 ζa可以根据实际情况选取。控制因子ζk的更新方法为[8]：

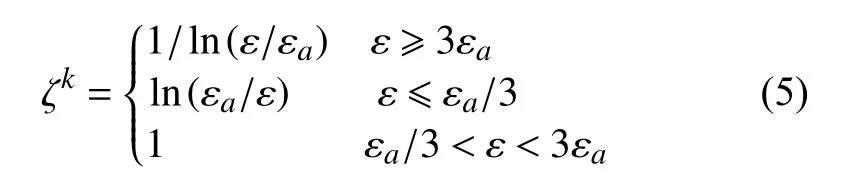
式中， εa为代理模型的容许精度，本文利用当前最优解的相对误差ε来估计当前近似方法的预测精度：

xk-1k-1式中，的取值为第次迭代时响应值最小的样本点。

1.2 全局加点模型

最大化Kriging 模型给出的设计点预测方差可以提高近似方法的全局预测精度，但是在实践中获得预测方差的最大值非常难，从而导致其性能改善程度有限。因此本文提出通过平衡变量和设计点的预测方差来综合确定设计空间中不确定性较大的区域，以提高模型的总体探索能力。数学描述为：

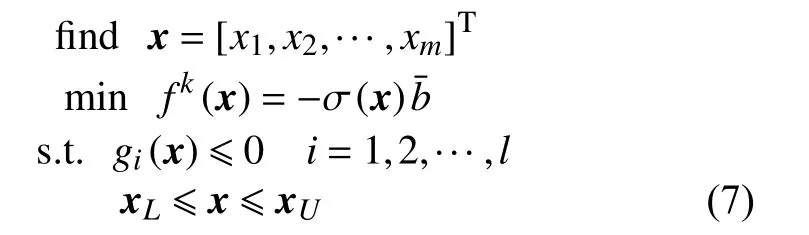
1.3 方法的实现流程

图1 为本方法的流程图，优化过程中的相关参数计算如下：

1)本文采用maximin 准则选取初始样本点，迭代次数设定为1 000。初始样本点个数同设计变量的个数m 有关，参考文献[10]中的选取办法：

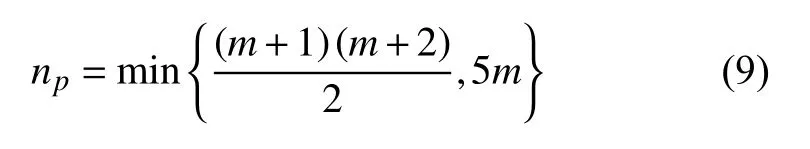
2)当包含有耗时约束时，利用文献[8]中的自适应罚函数方法进行约束处理，然后利用Kriging建立功能函数的代理模型。

3)收敛条件判断。当实际分析模型的计算次数达到设定的最大次数或连续两次迭代得到的最优解相对误差 Δ小于给定的收敛标准 Δa时，如式(10)所示，则停止迭代。

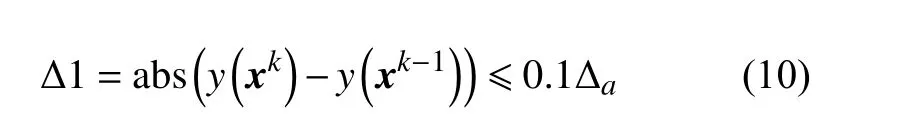
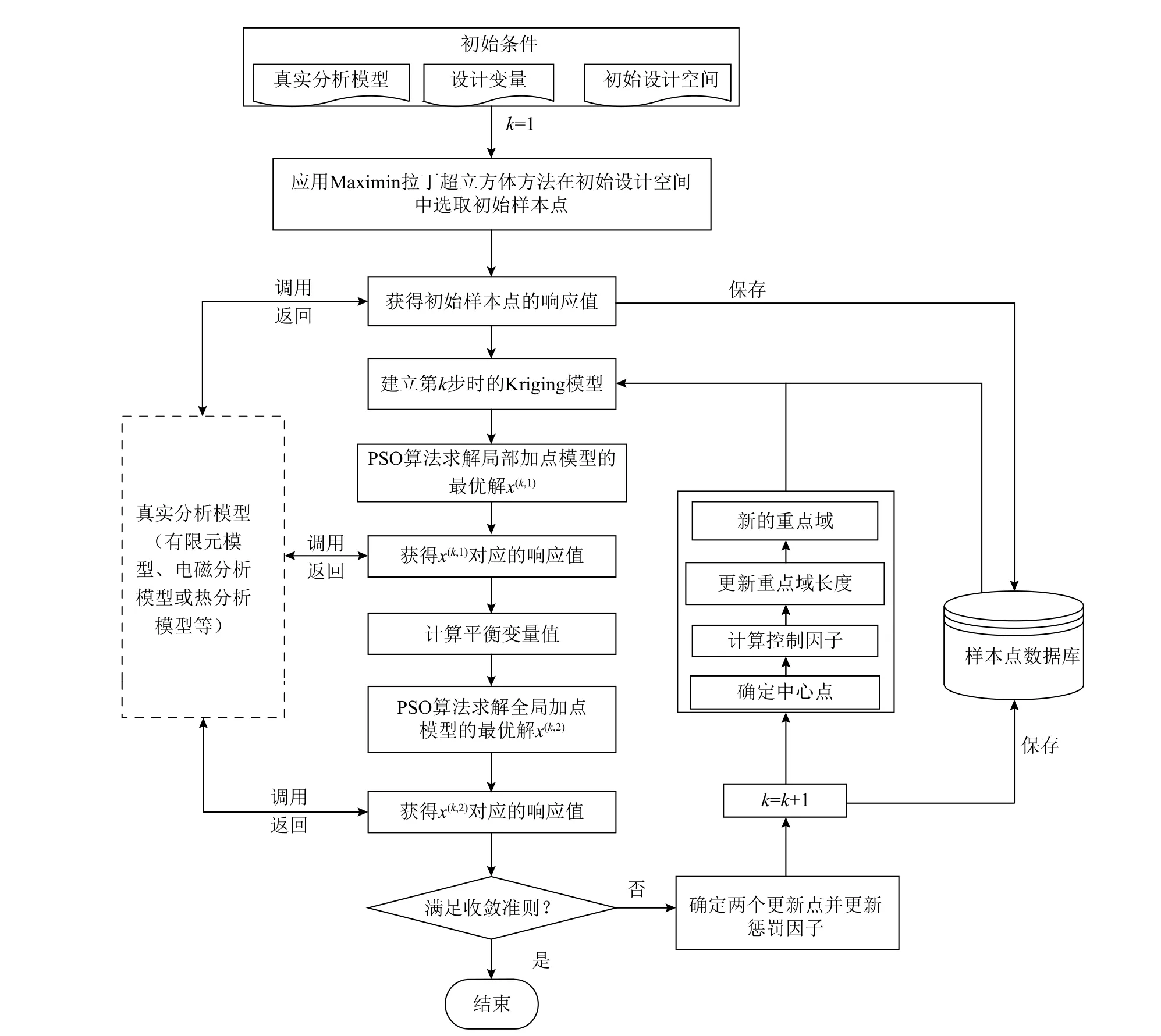
图1 本方法的流程图

2 测试算例

为了验证本文方法的有效性，特选取BR、SE、PK、SC、GN、HN6 等作为低维函数测试算例，选取R10、HD1、F16 等作为高维函数测试算例，以验证本文方法对不同维度问题的求解能力，表1为所有测试函数的相关信息，测试函数来源见文献[8]。

BR 函数表达式为：

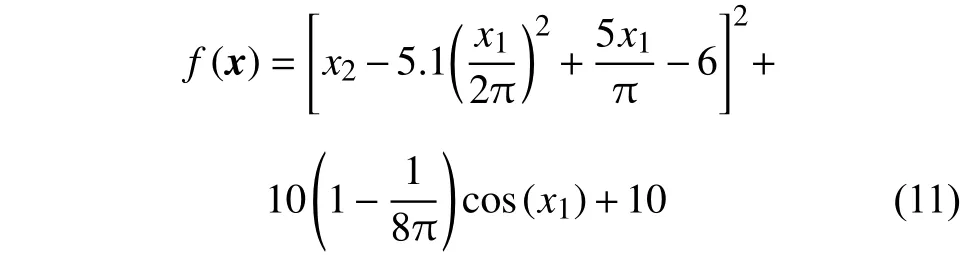
表1 测试函数的相关信息

SE 函数表达式为：

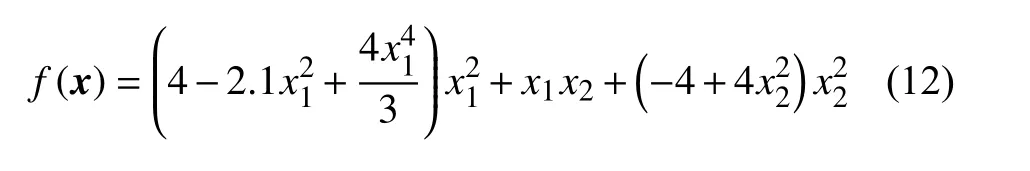
PK 函数表达式为：

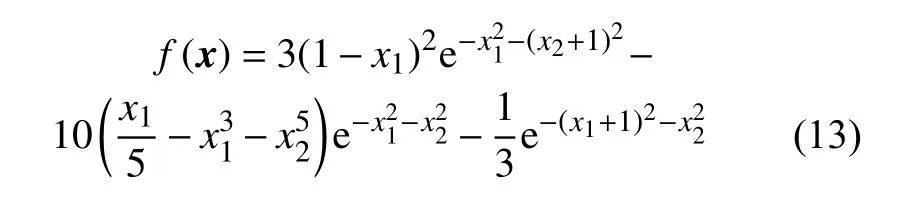
SC 函数表达式为：

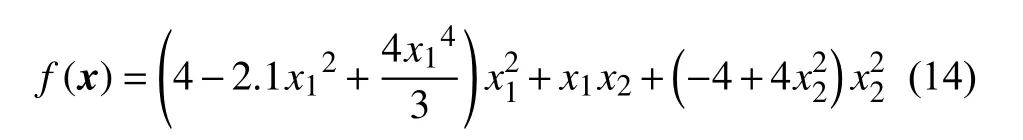
Hartmann 函数系列表达式为：

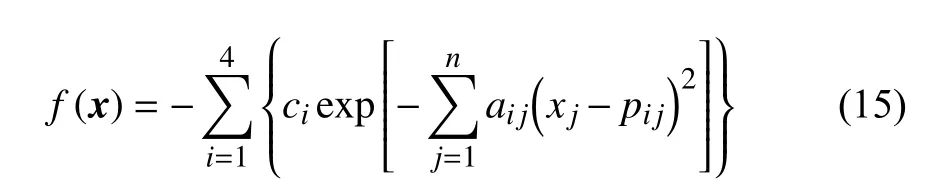
当n=6时，对应为Hartmann6 函数，此时系数a,p,c的取值参见文献[8]。

GN 函数表达式为：

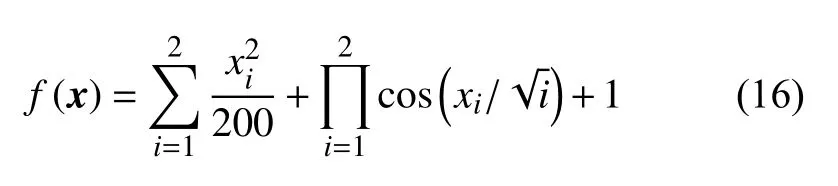
R10 函数表达式为：

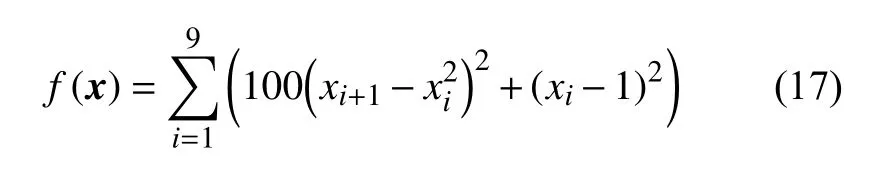
HD1 函数表达式为：

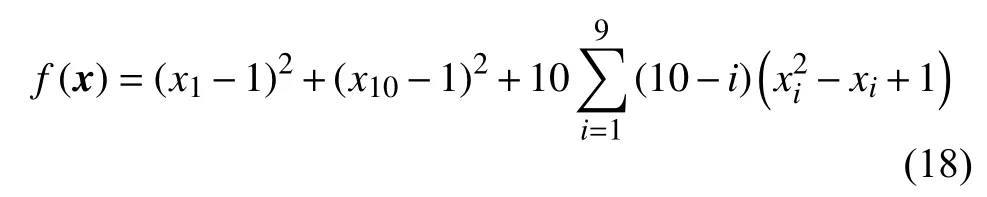
F16 函数表达式为：

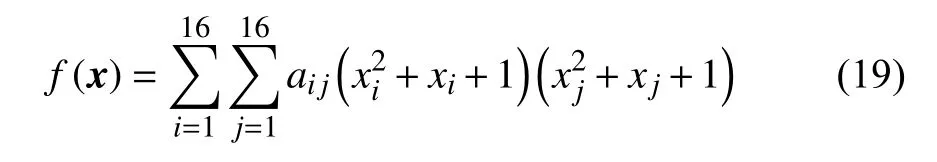
将本文方法同文献[5]中的EGO、文献[6]中的MPS 和文献[8]中的ARSM-ISES 方法进行对比。本文方法中Δa=0.005，εa=0.01， ζa=0.05，优化方法选用PSO，PSO 采用Brain Bridge 教授开发的工具箱，PSO 中种群个体数24、加速度参数为2、初始时的权值为0.9、结束时的权值为0.4，其他参数为工具箱中默认值。从理论上来说，EGO方法也可以用来求解高维函数的优化问题，但是由于EGO 方法的收敛速度慢，对于高维函数计算量过大，因此，高维函数中EGO 方法不做比较，后3 种方法的测试结果见文献[8]。为了保证优化结果的可靠性，在优化时需利用每种方法对每个测试函数连续优化10 次，每种方法得到的最终优化结果取10 次优化的中位值，表1 给出了测试函数的优化结果和最优解变化范围的对比，以综合评估几种方法的全局和局部预估能力及方法的稳健性。表2 给出了测试函数模型调用次数的平均值和其变化范围，以评估不同方法的优化效率。

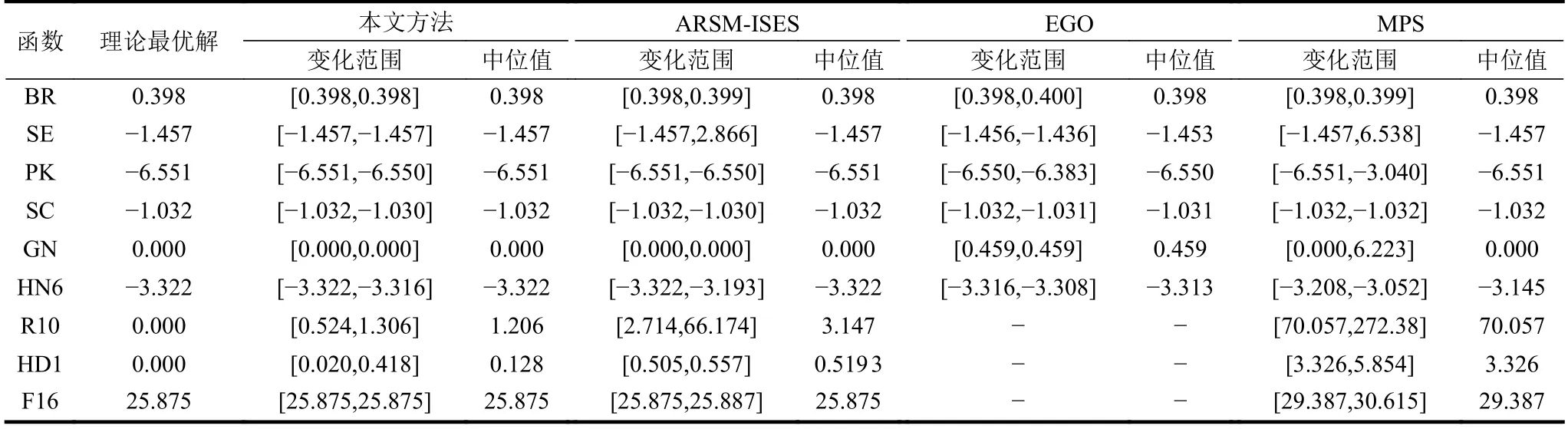
表2 测试函数的优化结果和最优解变化范围的对比

由表2 可知，对于大部分的低维测试函数，本文方法和ARSM-ISES 方法都能得到测试函数的理论最优解。对于GN 函数，EGO 方法所得优化结果同理论最优解相差较大，对于HN6 函数，MPS方法的结果同理论最优解有一定差距。针对高维函数，本文方法所得的优化结果同理论最优解最为接近，而且模型调用次数是几种方法中最少的，ARSMISES 其次，MPS 所得最优解最差。

模型调用次数是一种重要的表征代理模型优化效率的度量标准。由表3 可知，对于大部分测试函数，本文方法所用次数最少。对比于ARSM-ISES方法，两种方法虽然都引入了空间缩减技术进行模型管理，但由于本文方法中的代理模型使用的是近似能力更高的Kriging 模型，所以其优化效率和预测精度均有所提高。对于低维测试函数，虽然EGO 有着更高的优化效率，但其最优解对比于其他方法却是最差的。对于部分测试函数，MPS 的最小模型调用次数比本文方法都少，但是从表2 可以看出，引起这种情况的原因可能是由于MPS 方法提前收敛于局部最优解。

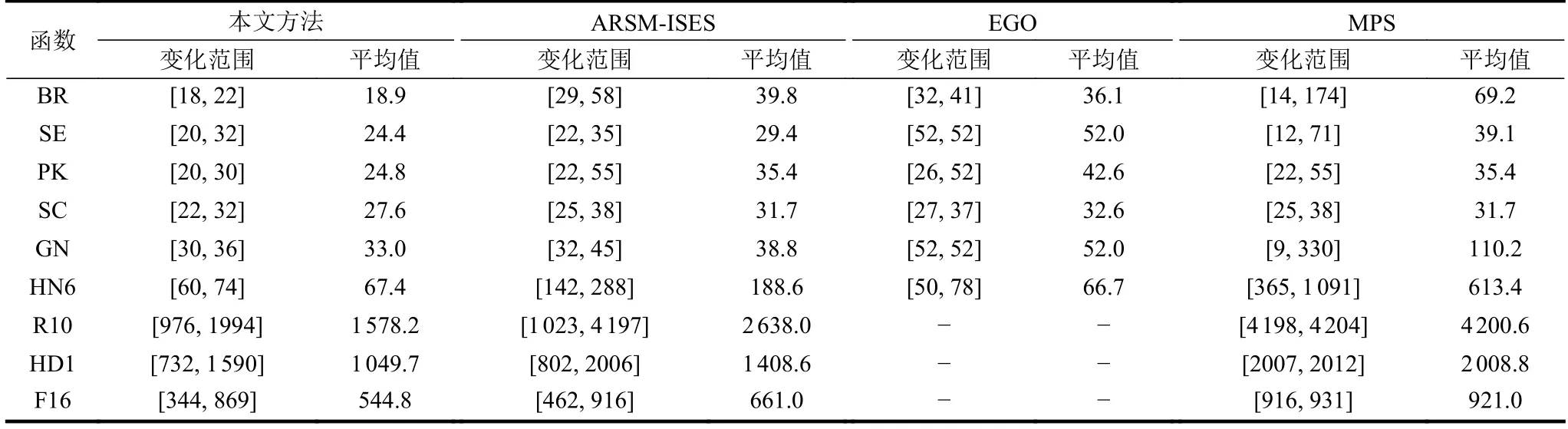
表3 测试函数的模型调用次数平均值和变化范围的对比

由上述对比可知，对于高维和低维问题，本文方法在计算效率和全局收敛性能方面上都有优势，有广阔的应用前景。

3 共形天线优化设计实例

共形天线作为武器平台的蒙皮结构，已经广泛应用到新一代战机、无人机、预警飞艇的机翼、机腹或机背等结构中[11]。图2 为该类型天线的基本结构，其中面板和蜂窝层具有力学承载功能，射频功能层实现电磁波的发送和接收，它主要由微带辐射单元阵列和对应的微波电路组成。

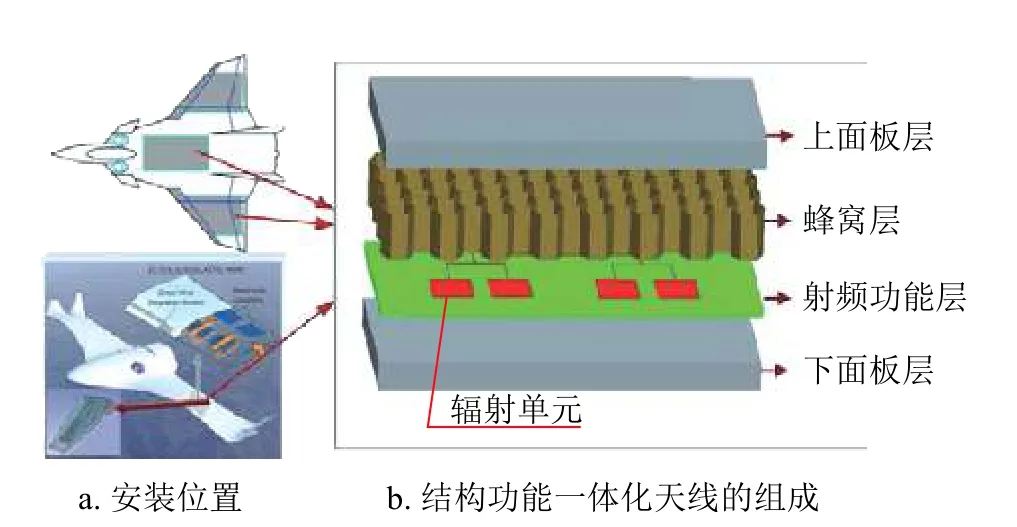
图2 共形天线的结构组成示意图

以天线的蜂窝层厚度 d1、上下面板层厚度 d2、蜂窝胞元壁厚 d3和蜂窝胞元壁长 d4为设计变量，长度单位都为mm，假设天线承受载荷为8 000 N，分析软件为ANSYS 和Matlab，最小化天线质量W，约束为天线的应力约束和位移约束。此时，建立的优化模型为：

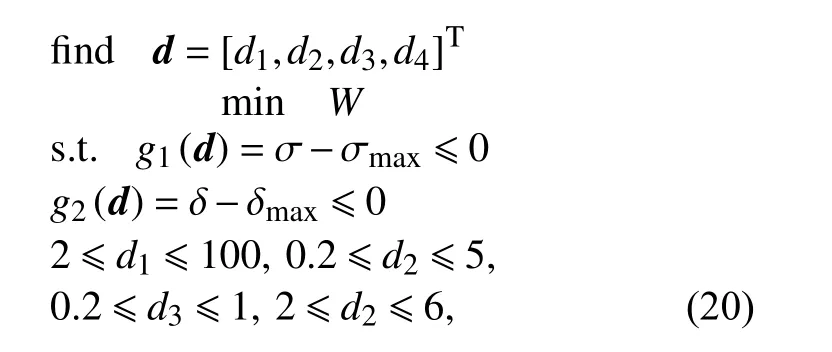
对于该优化问题，根据文献[11]的建议，本文中σmax=110 MPa，δmax=5 mm。将本文方法、EGO方法和PSO 方法(目标和约束都使用实际模型)对比，优化方法以及结果的选取方法同测试算例一致，所得结果如表4 所示。

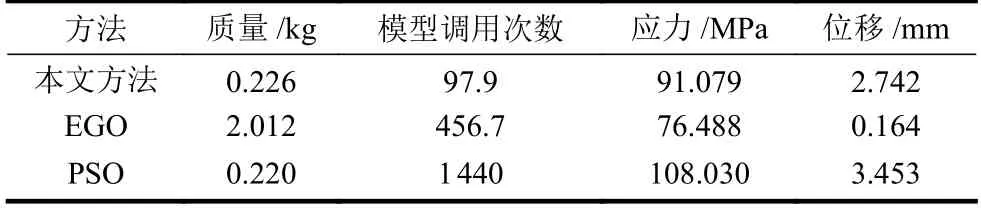
表4 优化结果对比

由表4 可知，PSO 方法所得结果最优，但是其计算量也最大。本文方法优化结果优于EGO 方法，且模型调用次数比其他两种方法都少。上述结果表明本文方法具有较好的实际应用能力。

4 结 束 语

针对复杂电子装备产品优化设计过程中计算量较大的问题，提出了基于重点域的自适应加点方法，在每次迭代时建立的全局加点和局部加点模型可以兼顾总体探索和局部开发。在局部加点模型中引入重点域可以提高局部开发的搜索效率和优化的收敛性，在全局加点模型中基于已有样本点信息建立的平衡变量可以提高Kriging 模型的全局预测精度。标准的测试函数算例和某共形天线优化设计的结果表明，同其他几种方法相比，本文方法不仅具有较高的全局收敛性，同时计算效率也有了很大的提升。在未来的研究中可将本方法应用于更多复杂的电子装备的优化设计中，并进一步探索更加高效的加点方法。