针对特定LDPC 码的多子译码器并行组合译码方法

张 哲，周 亮，周志恒

(电子科技大学通信抗干扰国家级重点实验室 成都 610054)

对于分组纠错码的译码，通过多个子译码器构建的并行译码系统比单译码器系统有明显的性能提升[1]。因此，较早即有多子译码器结构概念的Chase算法[2]和其变型的混合译码系统[3-4]。Chase 算法作为广义最小距离译码算法[5]的推广，它通过对软判决接收序列的不同似然门限选取和处理而获得多个待译码的“硬判决接收”序列，因此多个可并行实现的子译码器输出的候选码字为最后的最大后验概率原则提供了最佳码字的输出可能。在并行译码系统中，针对具体分组码的代数结构特性，设计和构造多个具有对同一信息数据进行不完全相同的校验译码的独立子译码器是一个挑战性难题。

文献[6]提出了一类称为MBBP (multiple-based belief propagation) 的方法，可以选取一个校验矩阵(即基础矩阵)扩展出多个不同的其他校验矩阵(即扩展校验矩阵)，再由这些扩展矩阵各自独立构成了一个子译码器。文献[7]提出的mRRD(modified random redundant decoding)算法结合了MBBP 思想和RRD(random redundant decoding)算法[3]来设计子译码器。其中，RRD 算法随机选取码的自同构群中的置换元素作用于基础矩阵来构造扩展校验矩阵用以译码，直到译码成功或达到次数上限时输出一个特定码字。

LDPC 码是分组码的一个重要子类[8-9]，其校验矩阵的构造途径多种多样，提供了实现多子译码器系统的较大可能。文献[10]在MBBP 的基础上，针对PEG(progressive edge-growth)算法[11]构造的LDPC 码提出了一种合并短环来获取扩展校验矩阵的方法。文献[12]提出一种由循环码构造的LDPC 码，利用mRRD 算法取得了并行译码的较大性能提升。这些MBBP 算法运用中的BP 译码模块所使用的扩展校验矩阵均需要具有良好的环结构，但是文献[6, 10]并没有给出相应的矩阵扩展方法。虽然mRRD 算法使用自同构群从一个具有良好环结构的校验矩阵扩展出具有相同环结构的矩阵。但是对于一般的LDPC 码而言却很难找到其自同构群[10,12]。

本文提出的多子译码器并行组合译码方法，与MBBP 算法不同之处在于新设计了包含两种子译码器的组合结构。第一种子译码器是扩展译码模块与基础译码模块级联，前者通过BP 算法输出辅助译码的外信息，后者确定候选码字。其中扩展译码模块的BP 算法迭代次数设置为其对应扩展校验矩阵中最短环长的一半，以此避免BP 算法受短环的影响。第二种子译码器则仅包含基础译码模块。这两类子译码器的输出的候选码字通过同一个LMS(east metric selector)依据最大后验概率原则筛选出最终译码码字。

本文提出的并行组合译码方法对由本原多项式生成的LDPC 码[13]尤为有效。这类LDPC 码编码开销极低，其码字是连接多项式是本原式的线性移位寄存器生成的序列片段。由此，本原式作为序列的零化约束关系可以转换为序列(即码字)奇偶校验关系。本原式对应特征向量的循环位移即为生成该码的基础校验矩阵。具体地，为了构建用于并行组合译码的子译码器的扩展译码矩阵，首先找出约束此LDPC 码的m 序列，再使用多个特定采样间隔进行采样获得采样序列；然后由采样序列获得约束它们的新本原多项式，并把这些新本原式对采样序列的约束转化为对码字序列的约束；最后，将这些新本原式的对应向量循环位移生成扩展校验矩阵。

本文使用本原式f(x)=x89+x38+1构造了码长3 000 的m 序列编码，并进行了误码率仿真实验。实验中构造了6 个由约束采样序列的本原式生成的扩展校验矩阵。此外，通过实验观察发现当子译码器个数为5 时，误码率曲线即有良好的收敛特性。误码率仿真结果显示，本文提出的并行组合译码方法比文献[13]中的单译码器译码算法有约0.4 dB的提升。

1 MBBP 算法以及mRRD 算法

1.1 MBBP 算法

MBBP 算法是一个多个子译码器构建的并行译码系统[6]，它的子译码器是由使用不同校验矩阵的BP 译码模块构成。图1 是MBBP 算法的结构，其中子译码器 D0中的基础译码模块使用基础校验矩阵H0对输入进行BP 译码，子译码器Di(i=1,2,···,N)中扩展译码模块则使用了扩展校验矩阵 Hi进行BP 译码。

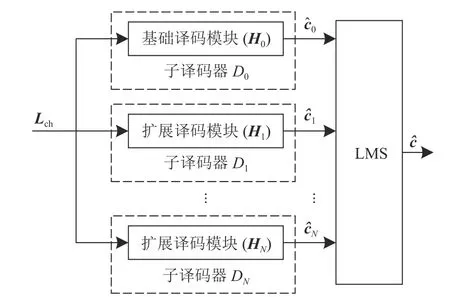
图1 MBBP 算法结构

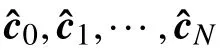
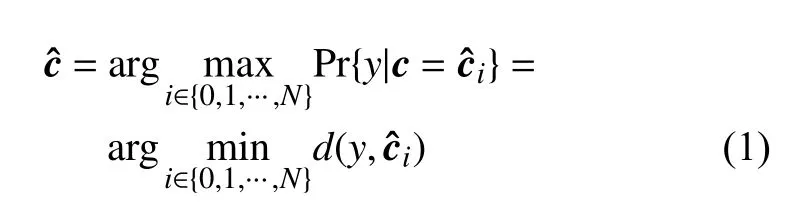
式中，d(a,b)是向量a 和b的欧几里得距离。

MBBP 算法的性能取决于子译码器输出候选码字的误字率及其等价的误码率，进一步地，依赖于各个子校验矩阵的环结构。

1.2 mRRD 算法

mRRD 算法与MBBP 类似，由N+1个完全相同的子译码器D0,D1,···,DN并行构成，但每个子译码器的内部构造与MBBP 算法不同。mRRD 算法的子译码器结构如图2 所示。

mRRD 算法第i 个子译码器 Di的译码流程是：

1)初始化：令θ为单位置换；令t=0；记BP 译码输入为L(0)=Lch；最大迭代次数为t0。

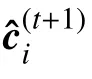
4)随机选取置换γ ∈Per(C)，令θ=θγ；将θ作用于基础矩阵 H0得到校验矩阵并记为Ht+1=g(θ,H0)；令t=t+1，回到步骤2)。

由于自同构群中的置换作用于基础矩阵后得到的扩展矩阵具有和基础矩阵一样的环结构，因此可以保证每个子译码器的误码率没有结构性恶化。显然，mRRD 算法构建的关键是找到码的自同构群。

2 多子译码器并行组合译码方法

对于构造LDPC 码的扩展校验矩阵的许多方法而言，不经意的方法会导致矩阵中的短环更短也更多，将其用于子译码器中的BP 处理时，难以有效改善译码性能。为获得适于多子译码器的扩展矩阵序列，本节首先分析短环导致译码性能恶化的机理和消除短环影响的途径，然后再给出一种可改善译码性能的扩展译码模块级联基础译码模块的子译码器结构。

2.1 BP 算法中短环的影响分析

BP 算法是在校验矩阵的等效Tanner 图上，计算变量节点的似然值并计算校验节点的信道外信息产出值，并在两类节点之间交换信息后再进行迭代计算的过程。若Tanner 图中存在由某个变量节点至校验节点再至其他变量节点并最终回返至原变量节点自身的较短连接回路(即短环)，则环中各节点的信息难以在足够多的节点中遍历足够的交互与平滑处理，从而导致变量节点的似然值估计存在较大误差。因此，短环较多的校验矩阵通常无法获得良好的译码性能。

图3 展示了Tanner 图中短环的信息流动情况，其中图3a 与3b 分别是4 环和6 环的情况。实线代表第一次迭代时候的信息传递，段状虚线和点状虚线分别代表第2 次和第3 次迭代时候的信息流。

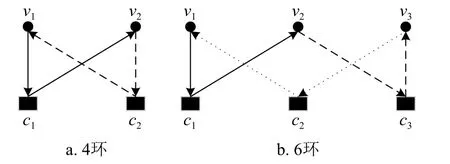
图3 Tanner 图中短环的信息流动

以图3a 为例，第一次迭代的信息通过校验节点 c1传给了 v2。第二次迭代的时候， v2把信息经 c2传回给了 v1，完成了一次循环。图3b 通过3 次迭代完成了一次循环。

从图3 可以看出，若迭代次数是短环环长的一半，则短环中流动的信息将不会再次流入原始起点，从而消除了由短环引起的节点信息估计存在误差的问题。

2.2 多子译码器并行组合译码方法

虽然，将BP 算法的迭代次数设置为校验矩阵的最短环长的一半，可有效消除短环在译码中的影响。但是，此时BP 算法无法输出有效码字。为了解决这个问题，本文提出一种在扩展BP 之后级联基础译码模块的组合并行译码方法，其译码结构如图4 所示。

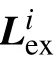
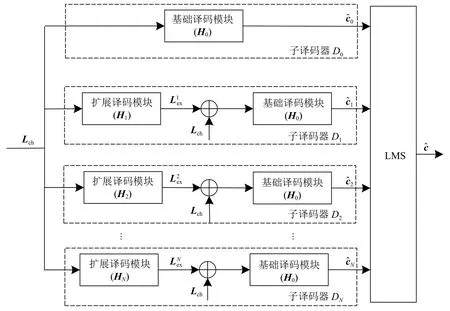
图4 并行组合译码结构

本文提出的并行组合译码方法的步骤如下：

1)初始化：设候选码字集合S =Ø；将信道接收值序列y的向量LLR 值 Lch分别输入到N+1个子译码器。

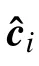
3)当N+1个子译码器译码结束后，若S =Ø，则译码结束并宣称译码失败。

3 本原式构造的LDPC 码及其扩展校验矩阵的构造方法

以本原多项式作为连接多项式的产生的线性序列是m 序列，m 序列的截段可以等价为一个LDPC 码的码字。这种LDPC 码可称为m 序列码[13]。由于m 序列产生器是一个线性移位反馈寄存器，因此m 序列码的编码开销极低。为了将并行组合译码方法应用于m 序列编码上，本节先介绍该码的编码方法，然后分析其采样序列的约束关系，最后给出用这种约束关系构造扩展校验矩阵的方法。

3.1 编码方式

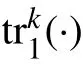
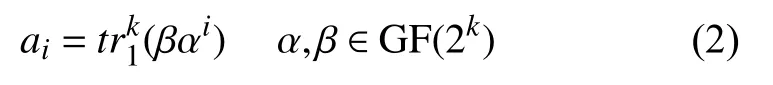
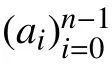
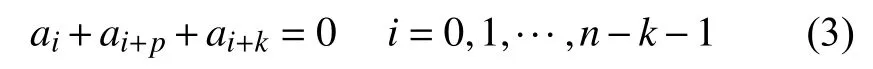
3.2 扩展校验矩阵的构造方法

由于GF(2k)可表示为本原元α的幂指数形式：

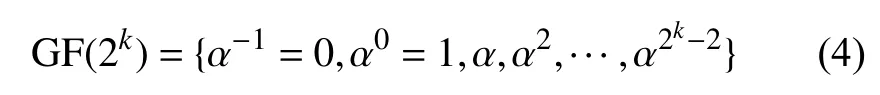
因此，αq∈GF(2k)是该有限域的本原元的充分必要条件为gcd(q,2k-1)=1，其中gcd(a,b)是a和b的最大公约数[14]。而且新找出的本原元 αq能代替 α重新表示整个有限域，即：

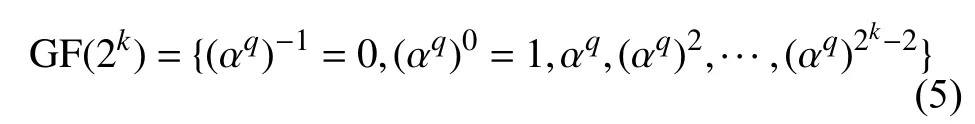
记本原元 αq是k阶本原式fq(x)的根，那么本原式fq(x)的形式为：

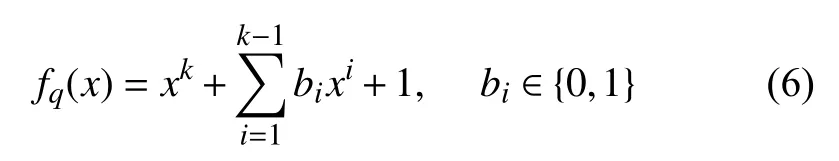
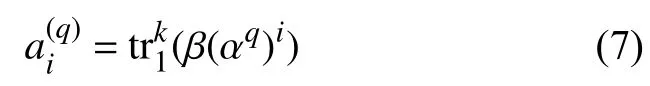
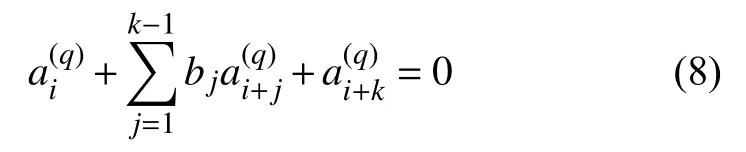
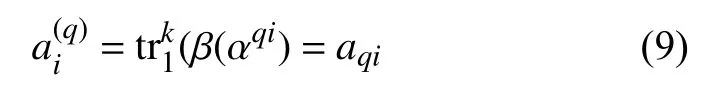
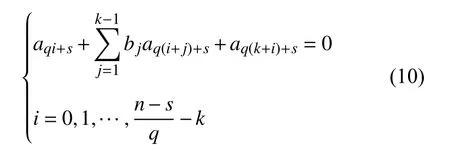
根据以上分析，本文设计了一种构造扩展校验矩阵的方法。为满足gcd(q,2k-1)=1的采样间隔q，构造扩展校验矩阵的步骤为：

1)生成f(x)约束下的m 序列 (ai)。

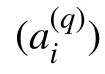
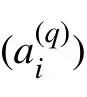
5)依照式(10)，将fq(x)对应向量做循环位移生成扩展校验矩阵。

由向量做循环位移生成的矩阵一定存在许多短环。因此，尽管该扩展校验矩阵不适合MBBP 算法中的子译码器，但是能用于本文提出的并行组合译码方法中的子译码器。

4 仿真验证

在深空通信和极低信噪比等场合，必须利用极低码率纠错码的极限纠错能力。为示范这类应用，本节构造一个极低码率m 序列LDPC 码，选择本原多项式为f(x)=x89+x38+1，设计码长为3 000，码率约0.03。仿真性能指标为误码率，对比对象为该码的单译码器译码算法[13]。

为验证子译码器个数对于误码率的影响，本文通过第3 节提出的方法，以采样间隔q=3,5,7,9,11,13构造出6 个扩展校验矩阵，对应的本原式fq(x)分别如下：

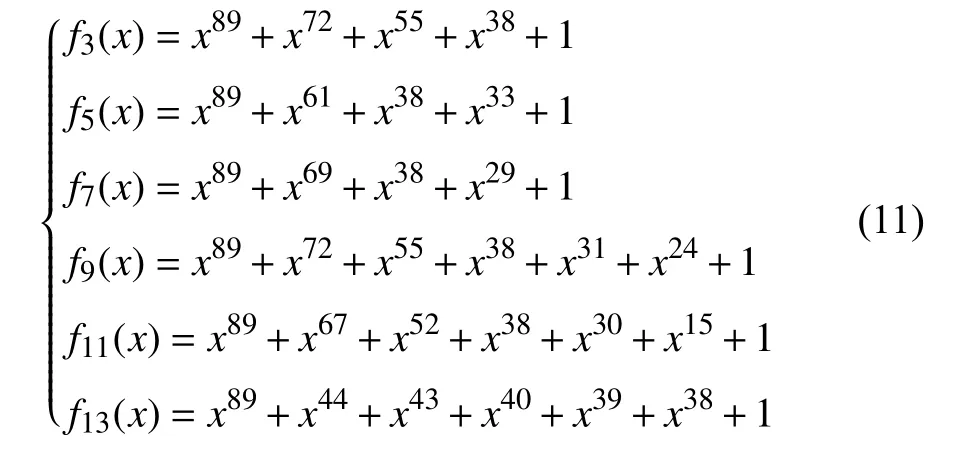
不同信噪比下误码率仿真结果如图5 所示。可见，译码性能随着子译码器个数增加而改善，但是子译码器个数大于5 后，译码性能趋于稳定。

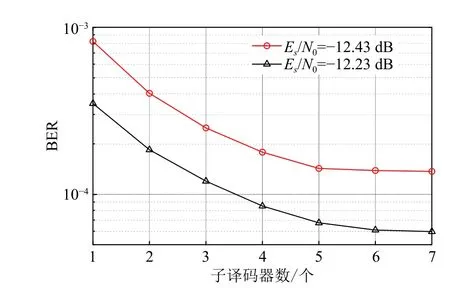
图5 子译码器个数的误码率曲线

图6 误码率曲线

图6 展示了不同译码方法下m 序列码的误码率曲线，从图中可以看出，本文提出的并行组合译码方法比原单译码器译码算法有更好的性能，当误码率为10-5时，本文的方法比原单译码器译码算法提升约0.4 dB。

5 结 束 语

研究和设计适用于分组码译码的并行译码系统是提高分组码纠错性能的又一条有效途径，适用于编码复杂度低但译码复杂度可宽容的，例如深空探测信息回传地球等通信场合。

本文提出了一种新的多子译码器并行组合译码系统，消除了子译码器中BP 译码模块里校验矩阵的短环对译码的影响，降低了构造适合的扩展校验矩阵的难度。针对m 序列编码，本文提出了一种构造扩展译码矩阵的方法，以适用于本文提出的并行组合译码方法。仿真实验显示，在误码率为10-5时，本文提出的并行组合译码方法比原单译码器译码方法提升约0.4 dB。