应对快速移动障碍物的多无人机编队避障控制
2021-04-09刘云平赵中原苗国英邓志良李炳志
刘云平,徐 泽,赵中原,苗国英,邓志良,李炳志
(1.南京信息工程大学 自动化学院, 南京 210044; 2.中国重汽集团济南卡车股份有限公司, 济南 250000)
无人机机群协同编队飞行技术具有机群覆盖范围广、活动半径大、机群整体搜索能力强以及效率高等优点,因此,适合战场环境侦察、战术打击和协同搜索等军事领域的各类复杂任务[1-3]。然而无人机机群在战场环境中编队飞行时可能遭遇快速移动的障碍物,若机群与之发生碰撞将导致任务执行失败。因此,对无人机机群在战场环境中的编队避障问题进行研究具有重要的理论意义和应用价值。
目前,无人机机群编队方法主要有跟随领航者法[4]、虚拟结构法[5]、基于行为法[6]以及一致性算法等[7-8]。一致性算法采用分布式网络进行信息交互,具有灵活性高和鲁棒性强等特点。因此,被广泛应用于无人机机群编队控制。无人机机群避障方法主要有人工势场方法、模型预测法(MPC)以及最优控制法等[2]。人工势场方法对计算能力要求低且实时性强,被广泛应用于无人机机群避障[2]。然而,无人机机群对障碍物的感知范围有限,当面对快速移动的障碍物时,无人机机群需要具有快速避障的能力才可成功避障。此外,当障碍物始终在无人机与目标点所在的直线方向移动,且移动速度大于无人机最大飞行速度时,基于传统人工势场方法的编队避障算法易陷入局部优化解,进而导致机群避障失败。
针对无人机机群编队避障问题,众多国内外学者研究并提出了多种算法。如Ruchti等[9]通过在传统人工势场方法上引入优先级模型和方向变化权重,改善了无人机之间的死锁情况,实现了快速避障。Ferreiravazquez等[10]通过将角度信息融入传统人工势场方法,并将其与一致性法融合,减少了局部最优化解对算法的影响,实现了机器人编队成功避障。朱旭等[11]通过在传统人工势场方法的基础上引入无人机与障碍物之间的相对速度,弥补障碍物无法主动规避无人机的缺陷,实现无人机机群快速避障。张佳龙等[12]通过将平行于x-y平面和y-z平面的两个势场复合成具有三维空间旋转矢量的人工势场方法,解决了无人机编队避障过程中易陷入局部最优化解的问题。这些学者的研究丰富了无人机机群编队避障理论,但都存在改进的空间。诸如文献[8-10]中的算法存在可能陷入局部最优化解的问题,上述研究都没有考虑无人机机群应对快速移动障碍物(障碍物移动的速度高于无人机最大飞行速度)时的避障问题。
本文研究战场环境下多无人机机群的编队避障问题,针对机群在执行任务时应对快速移动障碍物的情况,考虑障碍物始终在无人机与目标点所在直线方向移动且移动速度大于无人机最大速度的情况。通过在传统人工势场方法上引入辅助牵引加速度信息,提出一种改进的人工势场避障方法,实现多无人机快速避障,并克服局部最优对避障过程的影响。为提高多无人机编队过程的响应速度,本文将有限时间一致性算法与改进的人工势场避障方法相结合,提出一种无人机机群编队避障方法,实现无人机机群在飞行过程中快速编队与避障,提高了机群在战场环境的生存能力。
1 基本概念与控制目标
1.1 四旋翼无人机数学模型
本文采用参考文献[13]中建立的如下两个坐标系以更好的描述四旋翼无人机的运动状态:
惯性坐标系Exyz:坐标原点E为地平面上某一点;Ex轴正半轴为自坐标原点指向正东;Ey轴正半轴为自坐标原点指向正北;Ez轴的负半轴垂直于地平面并指向地球中心。
机体坐标系Bxbybzb:坐标原点B为四旋翼无人机的质心;Bxb轴正半轴为四旋翼无人机机头方向;Byb轴正半轴为四旋翼无人机机头方向顺时针旋转90度;Bzb轴正半轴为垂直于四旋翼无人机水平面且方向朝上。
四旋翼无人机从惯性坐标系Exyz转换为机体坐标系Bxbybzb的转换矩阵为(c=cos、s=sin):
(1)
其中,θ、φ和φ分别代表俯仰角,偏航角和翻滚角。
本文根据参考文献[14]建立第r架无人机的动力学模型为:
(2)
(3)
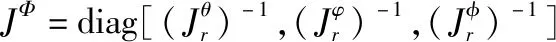
1.2 编队网络拓扑描述
假设无人机机群由1架虚拟领航者和n架跟随者构成。虚拟领航者按照指定的轨迹飞行,并将自身的位姿信息实时发送给指定跟随者。任意一架无人机均仅与有限架无人机进行信息交互。虚拟领航者与跟随者之间为单向通信(即数据仅从虚拟领航者发送至跟随者),跟随者之间为双向通信。其通信拓扑可用有向图表示为:G={v,ε}。其中v={v0,v1,…,vn}表示机群中各无人机节点的集合;ε⊆{(vr,vt)|vr,vt∈v,vr≠vt,r,t∈(0,1,2,…,n)}表示节点对的集合,也即各无人机之间的通信拓扑结构。设a为有向图G的邻接矩阵,art表示节点vr和vt之间的通信权重。若节点对(vr,vt)存在信息流通,也即无人机vr可以感知到vt,则art=1,否则art=0。
1.3 人工势场构建
本文构建的障碍物和无人机的势场及其影响范围如图1所示。对障碍物仅构建斥力场,对无人机同时构建斥力场和引力场。首先构建一个以障碍物s为势场中心,ro为半径的圆形障碍物斥力场。若无人机i进入障碍物s的势场影响范围内,即无人机与障碍物的距离小于最小安全距离,则无人机i受障碍物s的斥力场作用产生规避加速度auo,该加速度驱使无人机i远离障碍物s。同时本文引入了辅助牵引加速度avuo,以应对战场环境中快速移动的障碍物。

图1 人为构建的障碍物和无人机势场及其影响范围示意图

1.4 控制目标描述
四旋翼无人机机群中的虚拟领航者实时追踪目标点,各跟随者的飞行状态在有限时间内和虚拟领航者保持一致。机群能够在有限时间内形成指定编队队形,且能够持久的维持队形(各无人机保持相对位置不变)。在机群飞行过程中,无人机之间以及无人机与障碍物之间均不发生碰撞,且无人机机群在躲避障碍物后能够迅速恢复队形。本文假设无人机机群中至少存在一个跟随者可获取虚拟领航者信息,任意一个跟随者至少存在一个其他跟随者与之进行双向通信,且所有无人机之间的通信均同步。
2 无人机协同编队及避障控制算法
本节首先设计了基于有限时间一致性算法的编队控制算法,然后设计了基于改进人工势场方法的避障控制算法,并在此基础上提出了多无人机编队和避障控制算法。
2.1 基于有限时间一致性算法的多无人机编队控制算法
本文引入虚拟领航者以简化无人机机群的控制难度,故本文分别设计了虚拟领航者和跟随者的控制律。
首先设计位置控制律,改写式(2)中的无人机动力学模型如下:
(4)

定义vg以及Xg=[xg,yg]T表示目标点g的速度以及位置。则虚拟领航者0的位置控制输入设计如下:
(5)
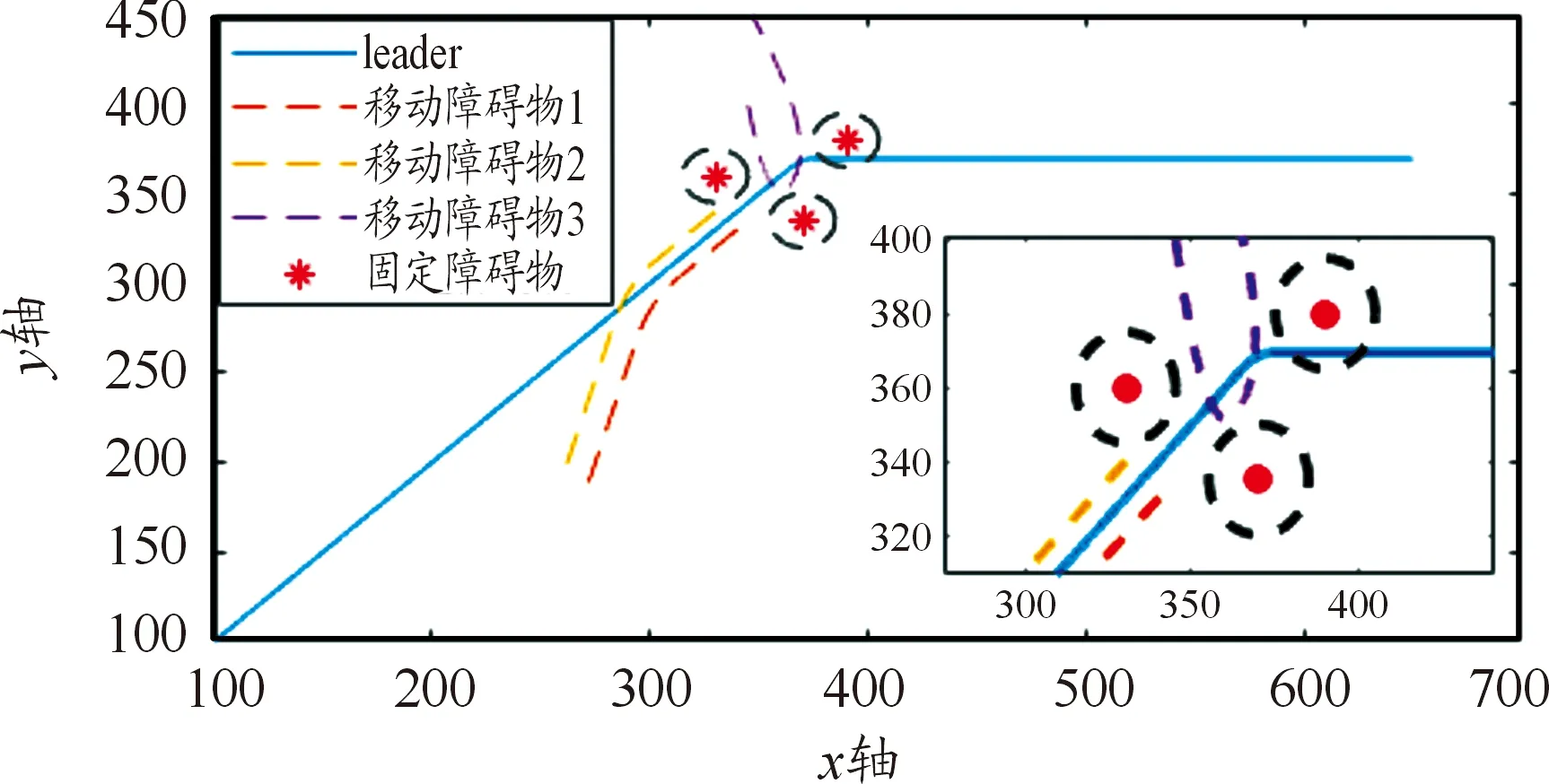
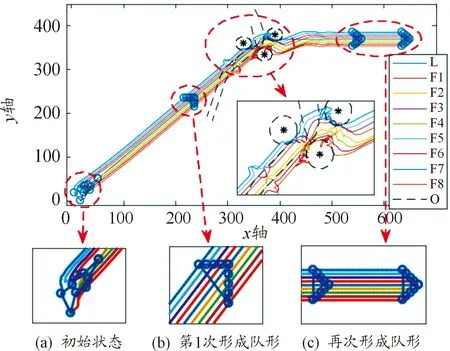
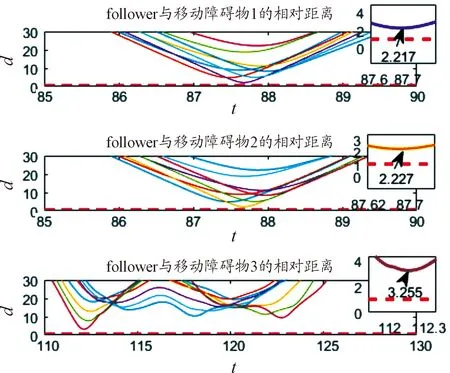
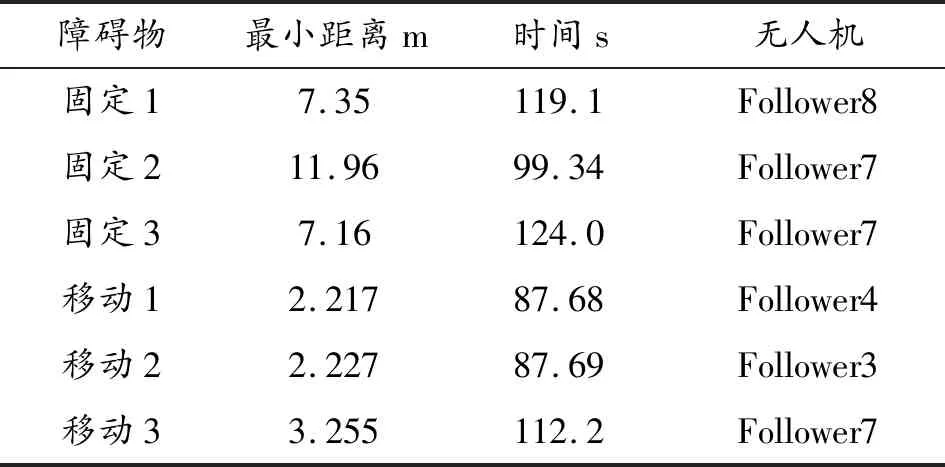
其中,0 在给出跟随者的位置控制律前,定义dXi表示跟随者i相对于虚拟领航者0的期望相对位置。令Xij=Xj-Xi,表示无人机i与j之间的位置;令hij=dXj-dXi,表示无人机i与j之间的相对位置。跟随者的编队控制输入设计如下: (6) 其中,i,j∈{1,2,…,n},b1~b4为调节参数,可调节算法的收敛速度。 然后设计姿态控制律,各无人机均采用相同的姿态控制律。改写式(3)中的姿态动力学模型如下: (7) 由式(4)可以推得无人机的期望姿态如下: (8) 则无人机的姿态控制输入设计如下: (9) 给出定理1的证明前,先介绍如下引理: 引理2:给定一无向拓扑图G,其Laplacian矩阵为L(A)=[lij]∈Rn*n,具有如下性质: (10) 针对式(10)构建Lyapunov函数VL=VL1+VL2+VL3。VL1、VL2以及VL3如式(11)所述: (11) 对式(11)中的3个函数沿式(10)求导可得: (12) 对构建的Lyapunov函数求导可得: (13) 由引理1得: (14) (15) 联立式(14)以及(15)可得: (16) (17) 因此,当t≥T0时,该有限时间一致性算法可实现一致性跟踪,即无人机机群在T0时刻可实现各无人机状态一致。 传统人工势场方法存在陷入局部最优化解的缺陷,本文通过引入一个额外的辅助牵引加速度来避免局部最优化解,该辅助牵引加速度与无人机以及障碍物的速度和相对位置有关,既可以作为扰动以破解局部最优化解,也可以作为一种能提高对移动障碍物避让速度的辅助加速度。 单无人机在空域中受障碍物势场以及各无人机势场影响而产生多个加速度,将各加速度叠加后即为无人机所受的合加速度。本文跟随者的避障控制输入设计如下: (18) 其中,auo和avuo分别为跟随者i在障碍物s的斥力场以及辅助斥力场影响下的规避加速度;auu为跟随者i在跟随者j势场(包括斥力场和引力场)影响下的加速度。 跟随者规避障碍物的的避障加速度设计为: (19) 定义vi表示跟随者i的速度,vs表示障碍物s的速度,l1表示跟随者i与障碍物s之间的连线,l2表示障碍物s为端点沿其速度方向的射线,θ表示将l2逆时针旋转至与l1重合的角度,α表示跟随者i和障碍物s两者移动方向之间的相对角度。跟随者的辅助牵引加速度设计如下: (20) 辅助牵引加速度的方向与θ有关。如图2所示,当0≤θ<π时,辅助牵引加速度的方向为沿障碍物s的速度方向逆时针旋转π/2;否则,辅助牵引加速度的方向为沿障碍物s的速度方向顺时针旋转π/2。 图2 辅助牵引速度示意图 跟随者的无人机间加速度定义如下: (21) (22) 进而,无人机编队与避障控制算法设计为: (23) 综上,本文通过引入辅助牵引加速度避免了算法陷入局部最优化解,同时该辅助牵引加速度也兼具辅助无人机快速避让移动障碍物的作用。此外,本文根据障碍物的类型和速度来调节编队和避障算法的权值,提高了机群避障的速度,避免了将编队和避障算法直接叠加时,机群在避障过程中可能受编队算法的影响而导致避障效果较差的问题。 本文利用MATLAB对算法进行验证。无人机机群由一架虚拟领航者和八架跟随者构成,编队的网络拓扑如图3所示。所有无人机以及障碍物的高度均为2 m,定义虚拟领航者和跟随者的初始位置坐标以及初始速度如表1所示。 图3 无人机机群的编队网络拓扑图 表1 各无人机初始状态 本文在仿真环境中设置3个固定障碍物和3个移动障碍物以模拟复杂战场环境。固定障碍物的位置坐标为(370 m,335 m),(330 m,360 m),(390 m,380 m);移动障碍物的状态如表2所示,其速度大于无人机最大飞行速度。 表2 移动障碍物的初始状态 本文定义无人机感知障碍物的最大范围为30 m。定义固定障碍物和移动障碍物的势场范围分别为15 m和10 m。 虚拟领航者的规划轨迹为:首先从3个固定障碍物中穿越,然后于105 s时改变飞行轨迹。移动障碍物1和2同时穿越无人机编队,移动障碍物3以U形轨迹在固定障碍物及机群中飞行。虚拟领航者的飞行轨迹、固定障碍物以及移动障碍物出现的位置如图4所示。 图4 虚拟领航者飞行轨迹以及障碍物示意图 图5 编队飞行轨迹 图5为无人机机群的编队飞行轨迹。图6为编队时各无人机的飞行速度曲线,图7为机群中各跟随者与3个移动障碍物的相对距离曲线。由图5和图7可知,当t=66.7 s时,无人机机群中各无人机状态实现一致。当t=87.68 s时,无人机机群遇到移动障碍物1和2;直至t=178.70 s时,无人机机群中各无人机的飞行状态再次实现一致。由表3可知,机群中各无人机与固定障碍物的最小距离为7.16 m,与移动障碍物的最小距离为2.217 m。 图6 编队飞行速度曲线 图7 跟随者与各移动障碍物的相对距离曲线 表3 与各障碍物距离最近的无人机的具体信息 本文同时测试了传统人工势场方法在如图4所示障碍物环境中的避障能力。经仿真后得到图8、图9、图10以所示的仿真结果,表4 为传统人工势场方法下与障碍物距离最近的无人机及其距离、时间。 图8 传统人工势场方法的编队飞行轨迹 图9 传统人工势场方法的编队飞行速度曲线 由图8和图9可知,无人机机群在遇到障碍物后,直至t=193.30 s时机群中各无人机状态再次实现一致。由图10和表4可知,机群中各无人机与固定障碍物的最小距离为9.6 m,与移动障碍物的最小距离为0.095 m。 图10 传统人工势场下跟随者与各移动障碍物相对距离曲线 表4 传统人工势场方法下与障碍物距离最近的无人机及其距离、时间 通过对比表3和表4可知,本文提出的算法在避让移动障碍物时,其最小距离为2.217 m,传统人工势场方法则为0.095 m。也即传统人工势场方法无法避让移动障碍物1和2,存在陷入局部最优化解的缺陷。对比图5和图8可知,在对固定障碍物1、3以及移动障碍物3的避障过程中,本文提出的算法牺牲部分应对固定障碍物的避障能力以成功避让移动障碍物3;而传统人工势场方法则因兼顾3个障碍物而导致机动幅度大于本文算法,进而导致利用传统人工势场方法的机群再次恢复编队所耗的时间比本文算法多14.6 s。因此,本文通过在人工势场方法中引入了辅助牵引加速度,并根据障碍物类型以及速度来调整各项参数后,提高了对移动障碍物的避让速度,并避免了算法陷入局部最优化解,使得无人机机群在战场中生存能力更强。 1) 针对战场环境中无人机机群的协同编队和避障问题,在传统人工势场方法的基础上引入辅助牵引加速度信息,并将平衡点改为平衡区域,提出一种应对快速移动障碍物的四旋翼无人机机群有限时间编队和避障方法。 2) 该方法克服了传统人工势场方法易陷入局部最优化解的缺陷,使无人机机群具有快速规避障碍物的能力,可以更好地适应战场环境。 3) 通过仿真计算验证了该方法可以使无人机机群快速的编队和避障。
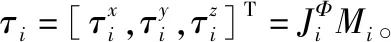

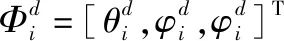









2.2 基于改进人工势场方法的多无人机编队避障控制算法









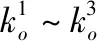
3 仿真实验及分析









4 结论
