一种用于海水DOC 微弱信号去噪处理的小波多阈值算法研究*
2021-04-08敏刘岩马然王昭玉
李 敏刘 岩马 然王昭玉
(齐鲁工业大学(山东省科学院)山东省科学院海洋仪器仪表研究所,山东省海洋监测仪器装备技术重点实验室,国家海洋监测设备工程技术研究中心,山东 青岛266061)
海水溶解性有机碳(DOC)一般是指能通过孔径0.45 μm 滤膜、并在分析过程中未蒸发失去的有机碳[1],它包括一部分未被滤膜阻留的胶体有机物质中的碳,来表示海水中溶解有机物质的总含量[2],是研究水体碳循环重要的一部分,在微量元素和营养盐的生物地球化学循环中扮演着重要角色[3]。 随着时间的推移,DOC 检测技术有了很大的创新和发展,但直至目前为止,现有的海水DOC 检测仍依靠现场采样到实验室进行分析的方法,存在操作复杂、耗时费力、时效性差等缺点[4-5]。 随着海洋监测范围在时间和空间领域扩大的需求,需要新的海水DOC 检测方法来克服长期存在的取样不足和无法原位监测的问题。 为了完成这些具有挑战性的海洋观测任务,一套具备精度高、响应时间短和长期稳定运行的海水DOC 测量仪势在必行。
国产化DOC 分析仪面临的主要问题是:仅适用于高浓度污染的水质检测,对于DOC 含量较低的海水不能适用;依赖国外昂贵的进口仪器,氧化管需要经常更换,不仅成本高,而且维护困难不满足海水DOC 的连续分析。 因此,研制一种可以在海洋恶劣环境下长期自动稳定运行的海水DOC 原位监测技术至关重要。 在此基础上刘岩[6]等发明了基于臭氧氧化化学发光测量海水总有机碳的方法,该方法利用微光转换技术采集化学发光反应过程中生成的光信号[7-8],优点是不受海水高浓度氯离子的影响,响应速度快,且避免了试剂会产生二次污染的影响[9]。 如何在气液混合反应产生的混杂信号中提取微弱的发光信号,是该方法应解决的重点和难点。目前,微弱信号的检测方法主要有窄带滤波、双通道去噪、同步积累法、锁相接收法、相关检测和采样积分法等[10-11]。 然而,无论采用何种方法,任何微弱信号的检测都必须将传感器采集到的微弱信号进行放大,同时还需要对放大后的信号做去噪处理,使信号不被更深层次的噪声信号淹没[12]。 目前,信号去噪的研究方法主要有传统滤波算法、神经网络、小波变换等[13]。 传统滤波算法存在关键信号和噪声难以优质分离的缺点,神经网络存在收敛速度慢的问题。 相较于以上两种方法,小波变换可以将信号中各种不同频率的成分分解到互不重叠的频带上,为信号滤波、信噪分离和特征提取提供有效途径[14]。
为此,本文基于臭氧氧化有机物发光的原理,利用光电倍增管(Photomultiplier Tube,PMT)采集反应室中微弱的化学发光信号,针对微弱信号的去噪问题,提出一种小波多尺度多阈值的去噪算法,最后开展测试样机在海试现场的测量数据、小波多阈值去噪后重构数据、以及实验室分析三方数据的对比试验。 通过臭氧流动注射保证测试样机连续监测的前提下,提高监测信号的信噪比,达到将微弱信号从噪声中优质分离的目的。 实验表明,小波阈值去噪重构后的数据与实验室分析数据比较接近,数据相关性超过78.5%。
1 实验方案
臭氧作为一种强氧化剂与处理后的待测水样进行气液混合反应,水样中的有机物被臭氧氧化后会产生微弱的化学发光信号,利用光电倍增管(PMT)检测反应室中化学发光量的大小,经微光信号检测模块转换为电信号后进行放大滤波等一系列处理,实现数字信号的有效输出。 实验系统结构方案如图1所示。
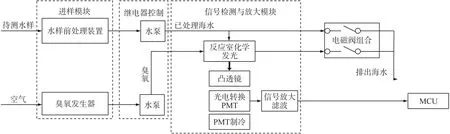
图1 实验系统结构方案图
微光信号检测和微弱信号去噪分析是微光信号处理的核心,将两个部分设计相互结合,在保证测量数据准确性的前提下,实现实时测量的最优化设计。
2 基于小波多尺度多阈值的去噪方法分析
海水DOC 原位监测分析的信号中包含大颗粒藻类产生的尖峰信号,对于这类突变信号的分析,需要较大的频率分辨率和较小的时域分辨率来体现突变的高频信息。 由于传统的傅立叶变换只能获取某段信号总体上包含的频率成分,无法对各成分出现的时刻进行获取,不存在分辨率的问题,因此传统的傅里叶变换对突变信号的分析无能为力。 而小波分析通过对尺度(a)和平移量(τ)的控制,将信号不同频率分量分解到各不重叠的频带上,实现信号频率有效成分和具体位置的提取。
2.1 小波阈值去噪原理
小波阈值去噪是通过小波确定分解层数对DOC 实验数据进行分解得到各层系数,通过构造相应的阈值,进行小波系数处理,输入信号分别与选定的母小波下构成的两个低通滤波器、高通滤波器做卷积运算,采样后得到信号的近似(低频)系数和细节(高频)系数。 保持每层的细节信息不变,对近似系数做下一步分解直至分解结束。 随着分解尺度的增加,有用信号大部分分布在较大的小波系数上,而噪声信号则分布在较小的小波系数上[15]。
假设传感器信号的模型是:

式中:t是传感器系统的输入,Y是其相应的输出。
根据多尺度系统的思想,存在一个唯一尺度函数φ(t)∈L2(R),它可以使信号f(t)在一个尺度上的近似表达式被写入下一个粗尺度上的近似表达式和细节信息之和[16]。
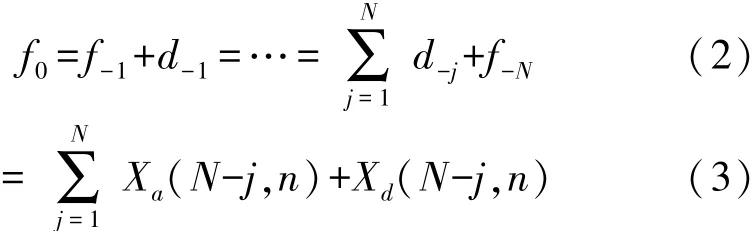
式中:d-j,Xa(N-j,n)是jth分解的详细信号部分,f-N,Xd(N-j,n)是jth分解的近似信号部分。 根据小波多尺度理论,随着尺度的增大,对应于信号的小波变换幅度增大,而对应于噪声的小波变换幅度减小[17]。 因此,在对传感器信号进行多次小波变换后,与噪声相对应的小波变换系数的幅度变得很小或者可以采用阈值法将其去除。 在小波域中,有用信号表现出较大的小波变换系数[18],而较小的小波系数大多由噪声和信号能量突变引起。 因此,通过设置阈值规则处理较小的小波系数,可以实现信号的有效去噪。
2.2 阈值函数
小波阈值去噪效果受小波基函数、分解层数、阈值函数等的影响,不同带噪信号设定阈值时需考虑选择合适的阈值函数。 传统的阈值函数主要有硬阈值和软阈值两种[19]。
硬阈值函数:
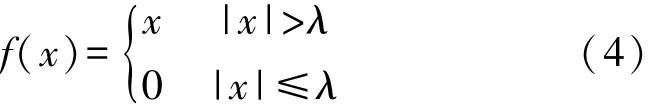
软阈值函数:
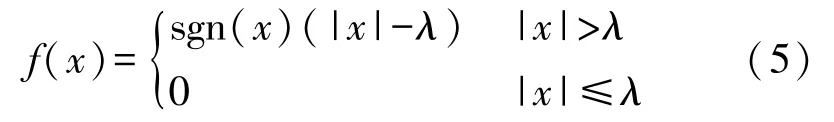
式中:f(x)为经阈值处理后的高频系数,x为高频小波系数, sgn(x)为符号函数,λ为阈值。
sgn(x)符号函数:
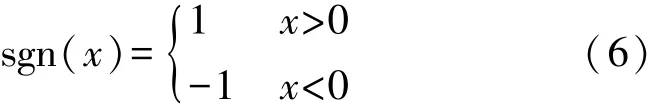
λ阈值:
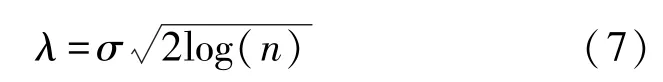
该阈值公式由Donoho[19]发明,阈值λ为最佳阈值上限,在很大程度上噪声的上限低于该值,因此各层阈值可根据信号的特点自由设定。 式(7)中σ为噪声标准差,通过高频系数绝对值的中值除以0.674 5 计算;n为每层小波高频系数长度值。
硬阈值函数和软阈值函数在应用中最为广泛,硬阈值函数能够较好的保持信号的局部信息,但由于阈值函数的不连续性,导致重构信号时会产生震荡现象;而软阈值函数连续性好,避免了震荡产生,但由于小波系数估计值和实际值之间存在偏差,导致信号重构时太过平滑致使有用信号缺失[20]。 为了得到更好的去噪效果,结合实际信号处理中对处理后信号的精确性和实时性并重的要求,在软硬阈值函数的基础上提出了以下改进阈值函数[21-22]。
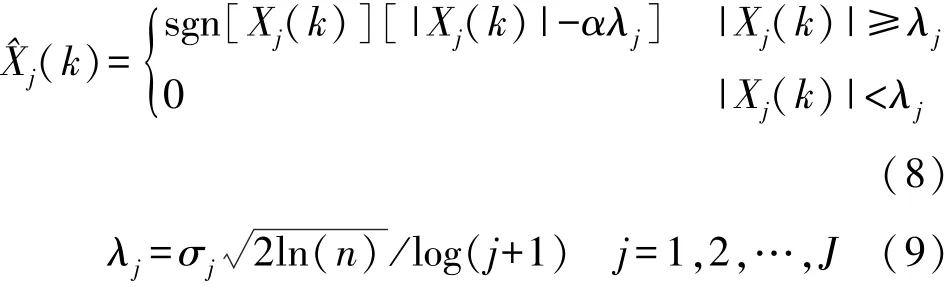
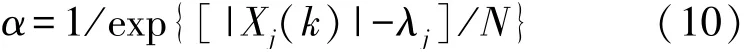
式中:N是预先计算的正常数据集,当N→∞时,式(8)是一个软阈值函数,当N→0 时,式(8)是一个硬阈值函数,改进后的阈值函数可以在软硬阈值之间灵活选取。
2.3 最优小波基的选取
去噪效果的好坏很大程度上取决于分解后的小波系数值和阈值参数的设定,而小波基决定了信号的分解和重构,影响小波系数值,进而影响去噪效果。如何选择最优小波基,主要考虑到小波基的特性。 例如:消失矩、正交性、紧支性、正则性、对称性等。 为了获得良好的去噪信号,小波基具备正交性能保证精准的重构信号;具备对称性保证滤波的线性相位,减少信号重构的失真;具备正则性则能使去噪信号有好的频域分辨率和光滑度[23]。 本文选择正交性、紧支性和正则性良好的db 小波,分析db2,db3,db4,db5,db8这五种小波基,通过去噪后的信噪比SNR 和最小均方误差MSE 作为比较标准选择最优小波基。
分析数据来源于搭建的测试样机在胶州湾各站点采集到的现场测量数据。 通过选择去噪效果较好的db 系列小波,对信号进行两层分解后,发现滤波后的数据与原始检测数据比对更接近。 图2 至图4是各小波基对信号去噪后与原始信号的效果对比图。 横轴为取样次数,间隔为1,纵轴为DOC 的值,单位是mg/L。
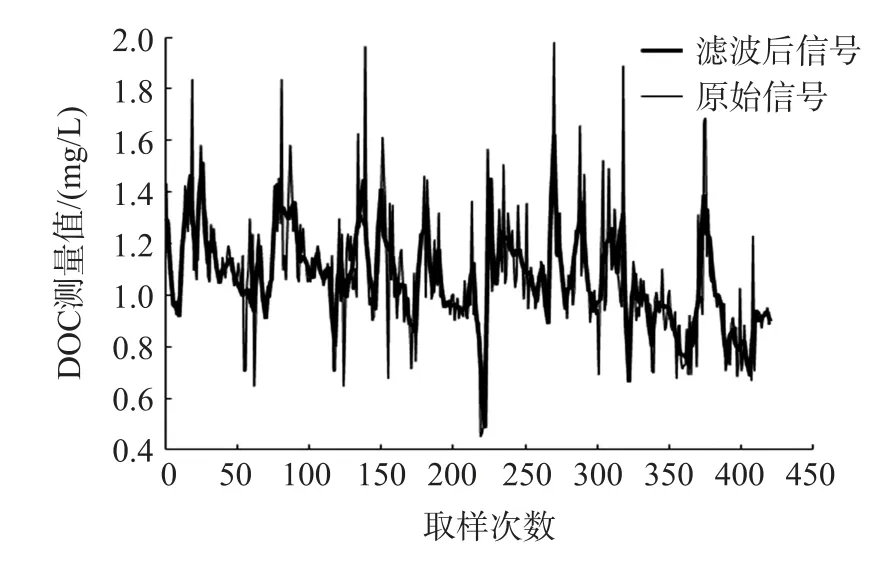
图2 db2 小波基滤波后信号与原始信号比较
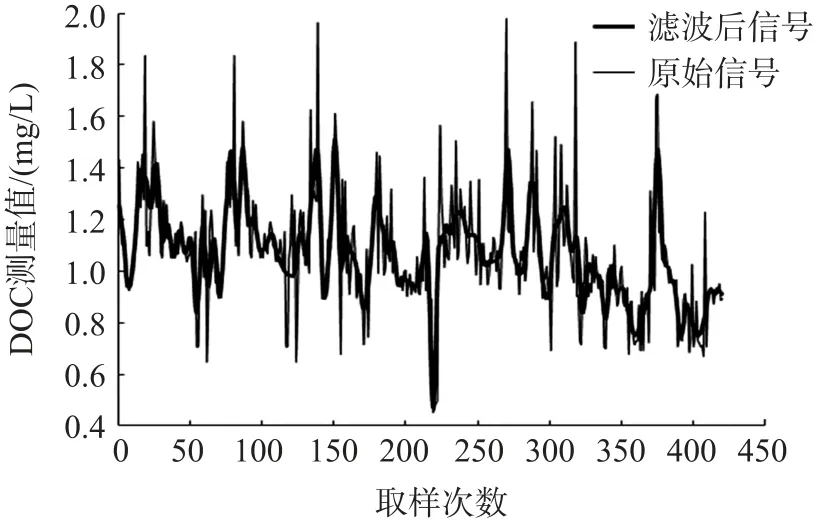
图3 db4 小波基滤波后信号与原始信号比较
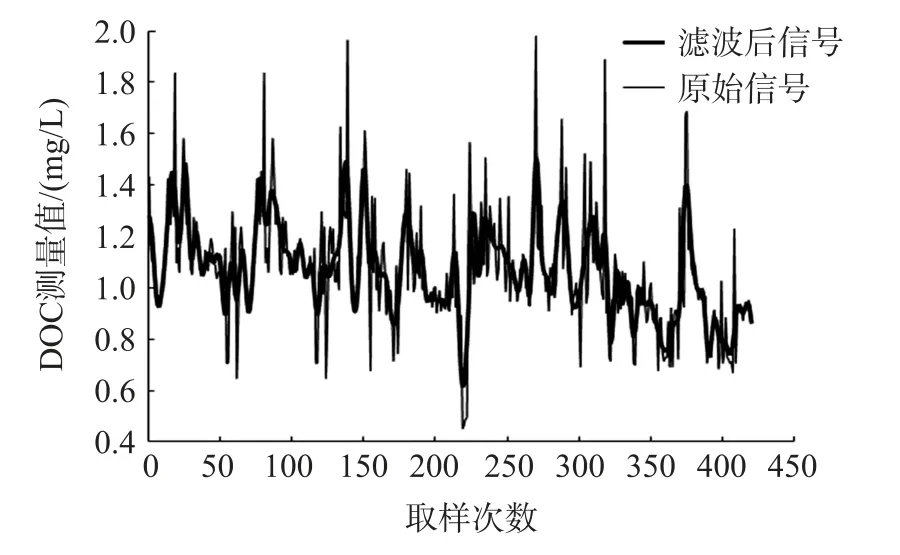
图4 db8 小波基滤波后信号与原始信号比较
由图2 到图4 可以看出db 系列小波很好的滤除了大部分高频噪声保留了低频信息,具体去噪效果好坏用MSE 和SNR 来评价,各小波基对原始信号去噪重构后的MSE 和SNR 如表1 所示。
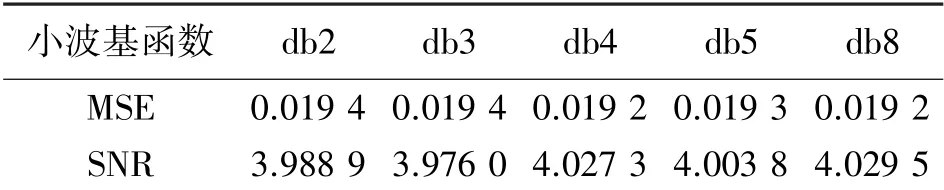
表1 DOC 数据去噪重构后的MSE 和SNR
由表1 可知对于DOC 实验数据,选定同样阈值条件下,db8 小波可以得到最小的MSE,和最高的SNR,由此得出结论:对于同一类型小波,支集较长的小波降噪效果较好,db8 小波优于db4 小波,db4又优于db2 小波。 所以本文采用db8 小波进行降噪分析。 基于db8 小波基下尺度1 到尺度5 的高频分解系数如图5 所示。
由图4 基于db8 小波基的滤波信号与原始信号比较和图5 db8 小波基d1~d5 尺度下的高频分解系数可以看出,通过db8 小波进行两层分解,分解后的高频噪声部分已经包含了很少的信息,如果继续进行分层处理,则会造成信号严重失真,如图6 所示。由图6 可以看出db8 小波进行3 层分解后,重构后的曲线太过平滑,重构后的数据与原始数据差值较大,造成信号失真。
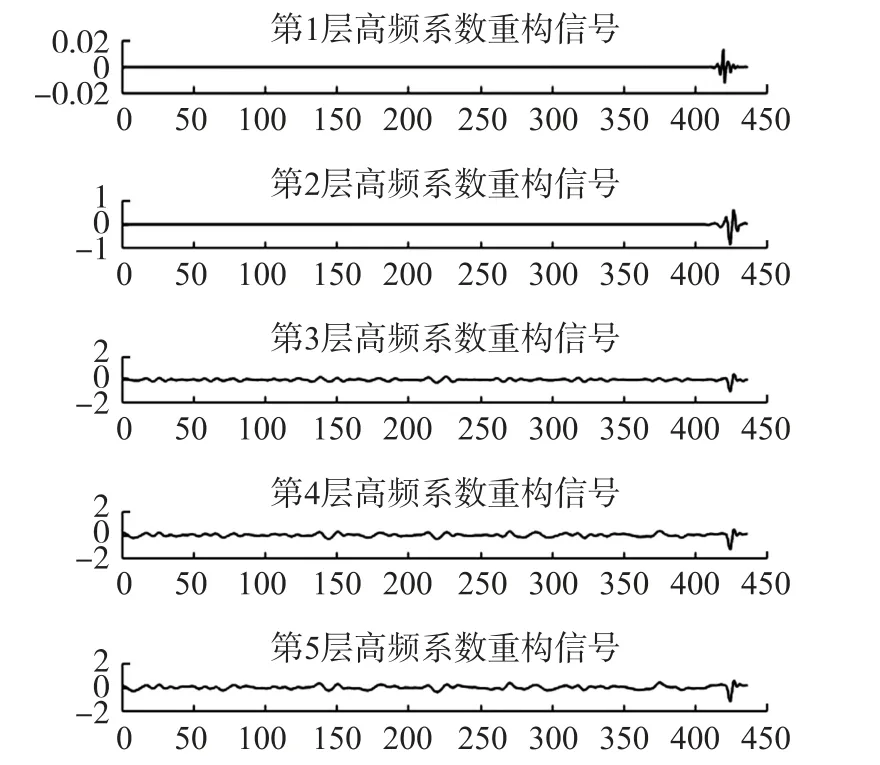
图5 db8 小波基d1~d5 尺度下的高频分解系数
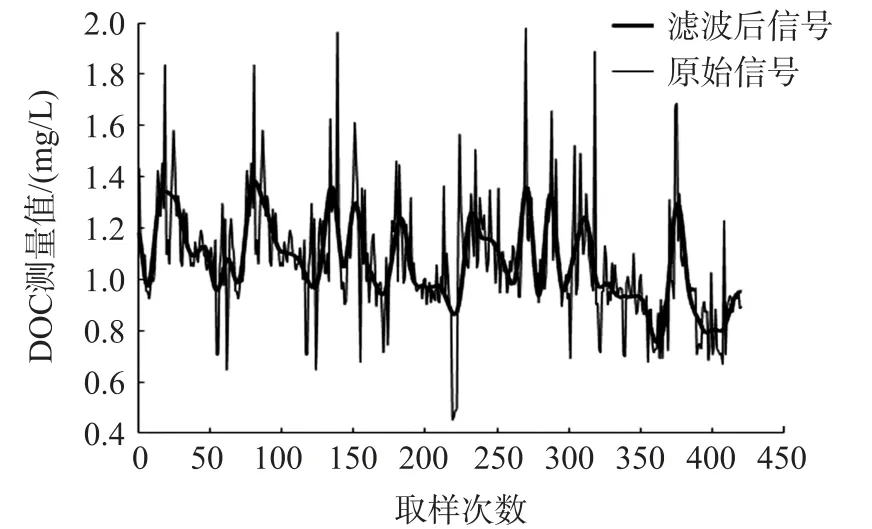
图6 db8 小波3 层分解滤波后信号与原始信号比较
3 实验分析
为了验证小波阈值去噪效果,选取试验船在胶州湾某个站点测得的部分实验数据与小波降噪重构后的数据进行比对分析,并将同种水样进行封存带回实验室分析,绘制小波降噪前后以及实验室测得的DOC 数据曲线如图7 所示。
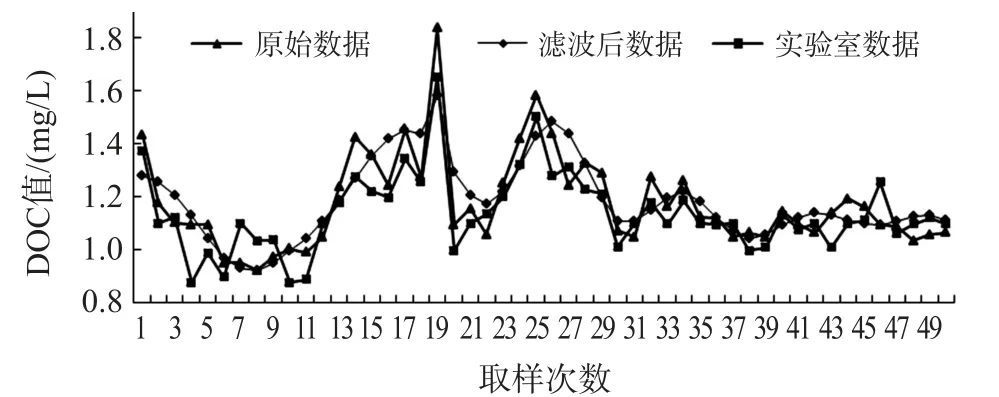
图7 小波降噪前后及实验室DOC 数据曲线图
通过观察图7 的三条曲线可以清晰得出如下结论:三者数据的吻合度较高,趋势基本保持一致;并且小波降噪后的曲线与原始数据曲线、以及同种水样的实验室测得数据曲线对比可以看出,db8 小波对信号进行重构后获得较好的平滑度效果,而且滤波后的数据与实验室测得的数据也比较接近,数据的相关性高于78.5%,能够满足国家对海洋原位监测仪器的要求。
4 结论
本文基于臭氧氧化发光法对海水DOC 进行原位分析,通过PMT 采集反应室的微光信号,针对光电转换后的微弱信号去噪问题,提出了一种新的基于小波多尺度多阈值的去噪算法。 该算法基于选择合适的小波基,通过去噪过程中在软硬阈值函数之间灵活选择,实现信号的有效去噪。 经过长期的现场海试试验,将臭氧氧化发光法测得的数据进行小波降噪重构后与实验室分析数据比对验证,证明采用臭氧氧化发光法可以实现海水DOC 的原位连续分析,与实验室分析方法相比,数据的相关性高于78.5%,证明该方法切实可行。 若将其应用于浮标体系的长期监测,可以实现对我国海洋环境有机物污染的有效预警,为海洋环境的监管提供可靠的依据。
