基于AR-MED和TEO的滚动轴承早期故障诊断方法

赵天升 常雪

1.中国船舶重工集团公司第七一三研究所，郑州 450015；2.重庆大学机械传动国家重点实验室，重庆 400044

0 前言

滚动轴承在机械设备的传动系统中起着重要的作用。由于滚动轴承实际使用工况复杂，发生故障的概率也相对较高。因此，及时有效地提取滚动轴承的故障特征，确保机械设备连续可靠运行，避免因突发故障造成不必要的损失是机械设备状态监测和故障诊断的研究重点[1]。在滚动轴承出现损伤的初期，故障特征信号通常较为微弱，且受到强背景噪声的干扰，因此，需要采用一种有效的方法对滚动轴承早期的微弱故障特征进行提取。

Teager能量算子（teager energy operator，TEO）由Maragos P与Kaiser J F[2]所提出，他能够对信号中所包含的瞬态特征进行增强，非常适合检测信号中的冲击成分。齐咏生等人[3]运用粒子群优化算法对最大相关峭度解卷积（maximum correlated kurtosis deconvolution，MCKD）的参数进行优化，并结合了Teager能量算子，完成了对滚动轴承复合故障特征的提取。王凤利等人[4]将参数优化后的集成经验模态分解（ensemble empirical mode decomposition，EEMD）与Teager能量算子相结合，对滚动轴承故障进行了有效地诊断。祝小彦等人[5]提出了多点最优调整的最小熵解卷积（multipoint optimal minimum entropy deconvolution adjuste，MOMEDA）与Teager能量算子相结合的故障诊断方法，该方法能够有效地提取故障信号中的特征频率成分。刘建春等人[6]首先依据谱峭度（spectral kurtosis，SK）对原始故障信号进行滤波处理，而后利用Teager能量算子增强信号中的冲击特征，通过包络谱分析法成功将滚动轴承内外圈的故障特征频率从原始信号中提取出来。

但是，Teager能量算子所具有的高时间分辨率特性导致其对噪声也比较敏感，在强背景噪声下提取滚动轴承故障特征的效果并不理想[7]。因此，有必要预先对滚动轴承故障信号进行滤波处理。

最小熵解卷积（minimum entropy deconvolution，MED）理论最早由Wiggins R A[8]于1978年所提出。Endo H等人[9]将其应用于齿轮箱故障诊断，取得了增强故障信号冲击性的效果。Sawalhi N等人[10]提出了将谱峭度与最小熵解卷积相结合的方法，并将其应用于滚动轴承的故障诊断中，取得了很好的效果。

滚动轴承故障信号含有周期性冲击成分、非周期成分和噪声成分，直接使用最小熵解卷积增强信号中周期性冲击成分的同时，也会对非周期成分有增强效果，导致信号的频谱受到非周期成分的干扰[11]。因此，为了削弱信号中非周期成分以及系统传递路径对周期性冲击成分的干扰，提高滚动轴承故障诊断的精度，提出一种融合自回归-最小熵解卷积（autoregressiveminimum entropy deconvolution，AR-MED）与Teager能量算子的滚动轴承故障诊断方法。利用AR-MED对原始信号进行滤波处理，达到增强信号中周期性冲击成分的目的，而后计算滤波后信号的Teager能量谱，提取故障特征，完成对滚动轴承早期故障的诊断。

1 基本理论

当滚动轴承出现局部损伤后，旋转部件与损伤部位接触后将形成冲击，周期性运转即形成循环冲击。与此同时，轴承各部件之间存在间隙及装配误差，运转过程中也会产生随机冲击。因此，传感器所采集到的振动信号是由故障引起的周期性冲击、轴承部件随机碰撞产生的非周期性冲击以及噪声共同叠加后的振动响应。设零均值平稳信号为[12]：

式中：yn——传感器采集到的振动信号；

xn——非周期性冲击成分；

wn——周期性冲击成分；

en——噪声；

hn——轴承系统的传递函数。

为了便于分析，暂时忽略噪声en的影响。对式（1）进行简化，可将xn与wn视为系统的输入量，而输出量则可表示为输入量与系统传递函数hn的卷积。

1.1 自回归（AR）模型

对于零均值平稳信号yn，且｛yi│i∈n｝可由其前i个值y1、y2、…、yi线性表示，由多元线性回归的思想，可得k阶自回归模型[13]，记为AR(k)：

式中：yi——待预测的第i个时间序列；

aj——AR模型的第j个系数；

k——AR模型阶数。

依据信号的自相关指标可以确定AR模型的系数。AR模型满足Yule-Wallker方程，即：

b(0)2——二阶统计特征；

δ——自相关系数。

将式（3）写成矩阵形式：

根据信号自相关的性质可知，信号中的周期性冲击成分仅与自身的相关性最高，而与其他噪声成分的相关性则较低。因此，对原信号进行AR滤波后，周期性冲击成分wn将从原始信号yn中分离出来，AR滤波后信号zn将由周期性冲击成分和噪声组成。即：

1.2 最小熵解卷积（MED）

峭度是描述信号中瞬态冲击成分的一个指标，峭度值越大，表明信号中的冲击成分越强。MED以峭度是否达到最大作为控制运算是否终止的条件。因此，对信号进行MED滤波，可以增强信号中的周期性冲击成分。具体运算过程如下：

（1）确定目标函数。Wiggis采用四阶累积量作为目标函数，目标函数取得最大值时所对应的解即为最优解。

其中：周期性冲击成分wi满足｛wi│i∈n｝；

Ok(f) ——目标函数；

k——累积量的阶数。

为使目标函数达到最大值，只需对式（6）求一阶导数，并令其等于0，如式（7）所示：

（2）依据所求得的最优逆滤波器系数fL，对输入信号zn进行解卷积运算，即可得到其中的周期性冲击成分wn。即：

观察上式可知，输入信号zn与输出信号wn的关系可由下式表示：

依据式（7）、（8）、（9）进行推导可得：

将上式变换为矩阵形式：

式中：f——逆滤波器系数；

A——逆滤波输入信号的Toeplitz自相关矩阵；b——输入与输出信号的互相关矩阵。

对式（11）进行矩阵逆运算即可得到逆滤波器系数：

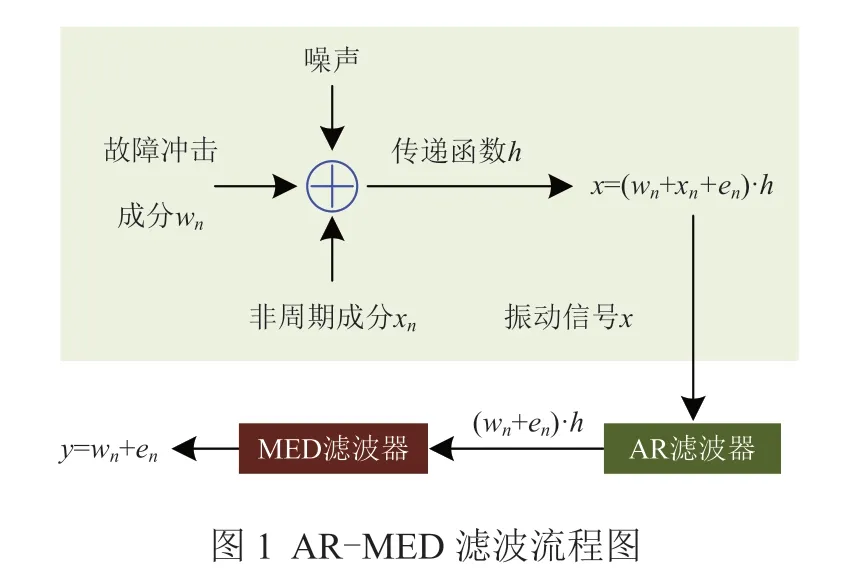
基于AR-MED的滤波流程如图1所示。

1.3 Teager能量算子（TEO）

连续信号x(t)的Teager能量算子ψc[x(t)]可定义为：

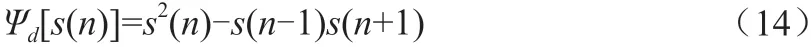
由式（14）可知，在计算离散信号的Teager能量算子时，仅使用3个数据点便可得到任意时刻n处的信号能量。因此，他具有计算简单、时间分辨率高等优点，适合用来检测信号中的周期性瞬态冲击成分。

2 基于AR-MED与Teager能量算子相结合的滚动轴承故障诊断方法

利用AR-MED构造的逆滤波器对振动信号进行解卷积运算，不仅可以得到信号中的周期性冲击成分，而且还能有效地削弱信号中噪声成分的干扰，为后续的故障特征提取过程提供便利。Teager能量算子具有时间分辨率高、计算简单等优点，非常适合作为后处理技术来检测信号中的冲击脉冲成分[14]。因此，为了充分发挥各自的优势，达到优势互补的目的，提出了融合AR-MED与Teager能量算子的滚动轴承故障特征提取方法。具体流程如图2所示。

3 仿真信号分析

根据文献[15-16]，滚动轴承外圈故障仿真信号可由下式表示：

式中：滚动轴承外圈故障仿真信号x(t)由周期性冲击信号s(t)和白噪声n(t)通过叠加得到；

Am——周期性冲击信号s(t)的幅值；

An——白噪声的幅值；

g——阻尼系数；冲击序列的周期，其中fc为冲击的频率，也是滚动轴承外圈的故障特征频率；

fn——轴承系统的固有频率。

为了模拟强背景噪声下滚动轴承外圈故障工况，设置冲击信号的幅值Am为0.5；噪声幅值An为0.6；阻尼系数g为2.5；周期性冲击的频率fc为125 Hz；系统的固有频率fn为1500 Hz；设定采样点数N=3,000；采样频率Fs=3,000 Hz。

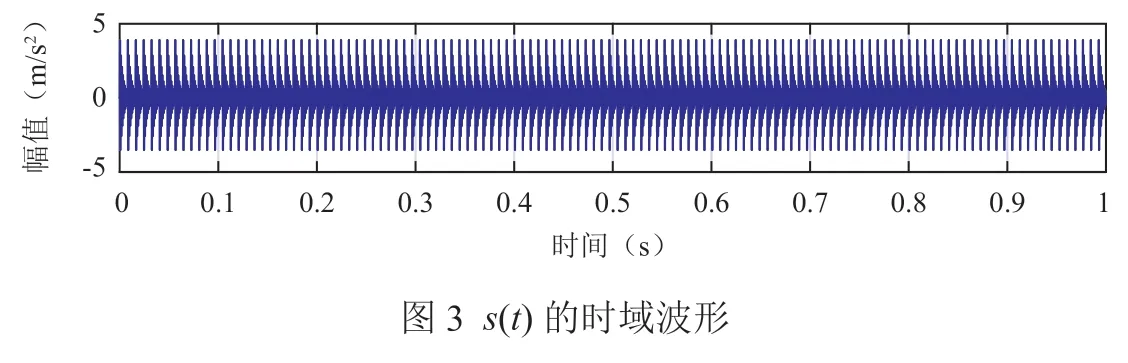
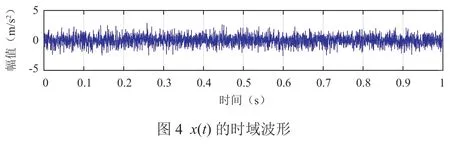
周期性冲击信号s(t)和仿真信号x(t)的时域波形如图3和图4所示。对仿真信号进行希尔伯特包络解调，其包络谱如图5所示。

对比图3、图4可以发现，仿真信号中的周期性冲击成分完全被噪声所淹没，从包络谱中也无法发现滚动轴承外圈的故障特征频率。

首先，对仿真信号进行Teager能量算子解调，其Teager能量谱如图6所示。

由于仿真信号中包含有强背景噪声，所以Teager能量谱中也无法找到明显的故障特征频率。通过上述分析可知，由于滚动轴承早期故障特征信号较为微弱，且受到强背景噪声的干扰，仅通过希尔伯特包络解调和Teager能量算子解调无法实现对微弱故障特征的提取。因此，有必要预先对信号进行滤波处理，削弱噪声成分的干扰。

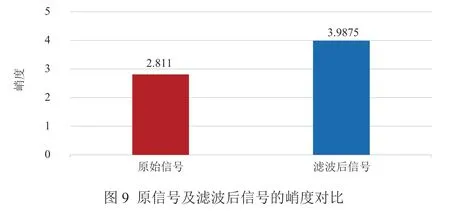
下面采用本文所提方法对仿真信号进行处理。首先，进行AR-MED滤波，滤波后信号的时域波形及包络谱如图7、图8所示。峭度是描述信号中冲击成分的统计量，分别计算原始信号以及AR-MED滤波后信号的峭度，如图9所示，可以发现，滤波后信号的峭度有了很大的提高。此外，通过观察滤波后信号的时域波形也发现其中包含明显的周期性冲击成分，由此可以说明，滤波后信号中的冲击成分得到明显增强，背景噪声得到有效抑制。

尽管滤波后信号的峭度得到了很大的提高，且包络谱中出现了滚动轴承外圈故障频率125 Hz，但125 Hz周围仍存在其他谱线的干扰，容易导致误诊断。因此，还需对滤波后的信号进行后处理。

求取滤波后信号的Teager能量谱，如图10所示，可以看到滚动轴承外圈故障频率125 Hz及其倍频，且无其他明显谱线干扰。

4 实验信号分析

实验数据采用西安交通大学设计科学与基础部件研究所提供的XJTU-SY轴承数据集[17]。轴承试验台如图11所示，主要由电机、电机速度控制器、支撑轴、滚动轴承、液压加载系统所组成。其中，实验轴承所受的径向力由液压加载系统施加，且可以在力显示器中实时显示负载值，电机转速则通过电机速度控制器进行设定。

实验中所用轴承型号为LDK UER204，具体参数如表1所示。

利用该试验台采集数据时，采样频率为25.6 kHz，采样点数为32,768。本文选取其中一组外圈早期故障数据进行分析，经计算，轴的转频为35 Hz，轴承外圈故障频率为108 Hz。

表1 试验轴承参数

实验信号的时域波形及包络谱图如图12、图13所示。

由于测试滚动轴承尚处于早期故障阶段，且信号中伴随有强背景噪声，因此时域波形中难以发现明显的周期性冲击特征。在包络谱中，也仅仅发现了轴的转频35 Hz及二倍频70 Hz，并未出现外圈故障的特征频率。

求取实验信号的Teager能量谱，如图14所示。对比图13与图14可以发现，相比于图13，图14中的谱线更明显，但却依旧只能观察到轴的转频35 Hz及二倍频70 Hz，所以仅对故障信号进行Teager能量谱分析难以实现早期故障特征的提取。

采用本文所提方法对实验信号进行分析。图15、图16所示为AR-MED滤波后信号时域波形及包络谱。对比图13与图16可以发现，滤波后，信号中的噪声成分得到了很好的抑制，实现了增强原信号中的周期性冲击成分的目标。

观察AR-MED滤波后信号的包络谱，不仅可以发现轴的转频35 Hz及二倍频70 Hz，还可以观察到轴承外圈故障特征频率108 Hz，但并不突出，且存在其他谱线干扰。这也表明，仅对原始信号进行AR-MED滤波处理并不能实现微弱故障特征的提取。

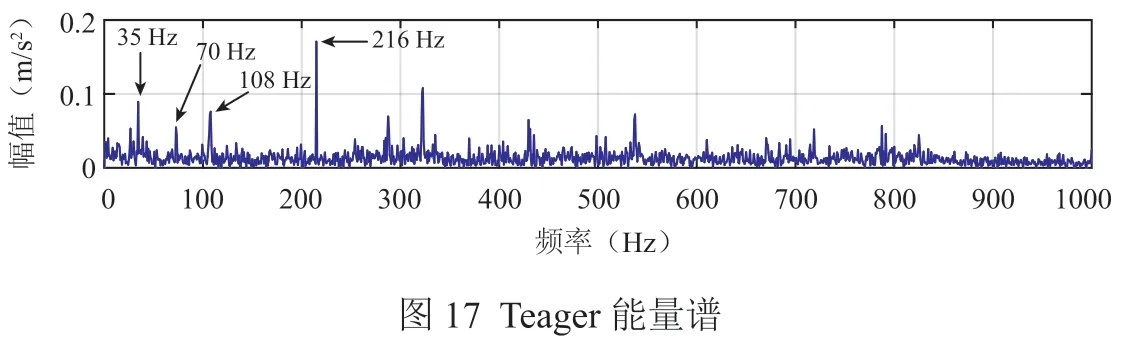
对滤波后信号进行Teager能量谱分析，如图17所示，Teager能量谱中不仅出现了轴的转频35 Hz及二倍频70 Hz，还出现外圈故障频率的一倍频108 Hz、二倍频216 Hz，相比图16，图17中故障特征频率更加明显。

实验信号分析结果表明，本文所提方法能够将滚动轴承早期较微弱的故障特征从原始信号中提取出来，并且与传统的包络谱和Teager能量谱分析方法相比，本文所提方法具有更为优异的分析效果。

5 结论

针对滚动轴承早期故障信号信噪比低、特征提取困难等问题，提出了一种融合自回归-最小熵解卷积和Teager能量算子的滚动轴承早期故障诊断方法，并采用仿真信号和实验信号分别对该方法加以验证，主要结论如下：

（1）滚动轴承早期故障信号中的故障特征较微弱且伴随有噪声，采用单一方法如包络谱分析、Teager能量谱分析难以实现微弱故障特征的提取；

（2）通过仿真和试验结果可以判断，ARMED确实能够有效地增强故障信号中的冲击成分。预先对滚动轴承故障信号进行AR-MED滤波，不但可以削弱系统传递路径以及信号中的非周期成分对故障特征提取的干扰，而且还能达到增强信号中的周期性冲击成分的效果；

（3）通过对AR-MED和Teager能量算子进行合理的结合，实现了优势互补，达到了抑制噪声干扰、增强故障特征的目的，并通过对仿真信号与实验信号进行分析验证了本文所提方法的可行性和有效性。