牵连体速度问题解析

湖北 许 文

在运动的合成与分解中，牵连体速度问题尤为常见。对于这类问题学生往往因不能正确判断物体合运动与分运动的关系，导致求解出错，特别是涉及动滑轮的牵连体、杆的牵连体等速度问题。运动物体的速度按矢量运算法则可任意分解，但牵连体的速度存在某种关联，这种关联受具体物理情景的制约，不能一概而论。速度按矢量法分解没有错误，但分速度是否有关联呢？这要受具体运动制约，因此这一点与力的分解有所不同。本文通过实例分析，帮助同学们有效地理解合运动与分运动关系，拓展解决牵连体速度问题的思维方法。

一、常规问题分析

【问题】如图1所示，人用绳子通过固定在岸边的定滑轮以不变的速度v拉水面上的小船，假设小船只在水平方向上运动，不计水的阻力。当绳与水平方向成θ角时，小船的速度v1的大小是多少？

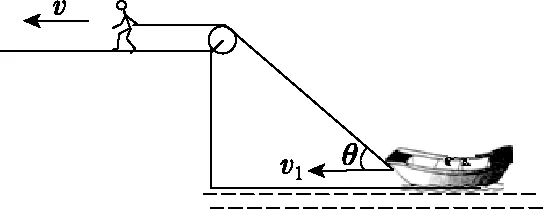
图1

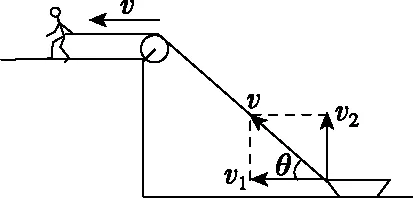
图2

【错解】处理这种问题，大多数同学几乎不假思考地把力的分解方法迁移过来，简单地认为绳与船连接点(绳子末端)的速度v是船运动的合速度，按如图2所示的分解方法将速度v进行分解，从而得出v1=vcosθ。

【质疑】1.从力的观点看：根据牛顿第二定律可知，绳子对小船拉力的水平分力Fx会使小船在水平方向上不断加速，实际上小船的速度v1应不断增大。小船向左运动过程中，角θ不断增大，可知cosθ不断减小，即以上答案中v1是不断减小的，与实际不符合。

2.从运动的观点看：设在一段时间Δt内小船在水平方向向左运动的位移大小为Δx，绳子拉出的长度Δl=l1-l2。如图3所示，由几何关系有l1-l2=Δl<Δx，即实际上有vv1=vcosθ，与实际不符合。

出现以上错解的原因在于对船的合运动与分运动认识不清。物体实际的运动是合运动，某时刻小船的实际速度v1是合速度。那么船的分运动是什么？怎样将船的合运动进行分解？

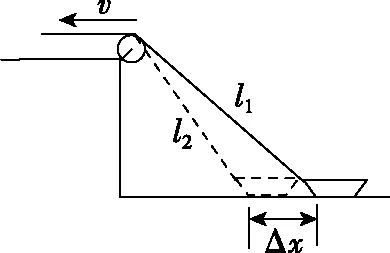
图3

【类比】如图4所示，一只小猴子悬挂在树藤的一端，从与水平桌面等高处摆下，如果它想抓到水平桌面上整齐排列的所有桃子，那么猴子应同时做两种运动，即绕绳子悬挂点O的圆周运动与沿绳子向上的攀爬运动。而我们看到猴子的实际运动是水平方向的直线运动，这是猴子的实际运动，实际运动是合运动。所以可以将猴子沿水平方向上直线运动的合速度v分解为如图5所示。

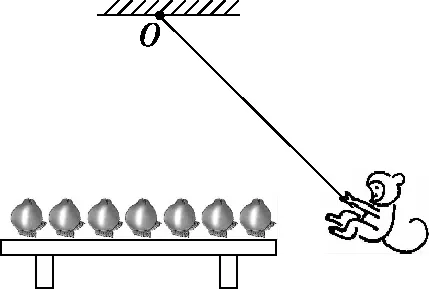
图4

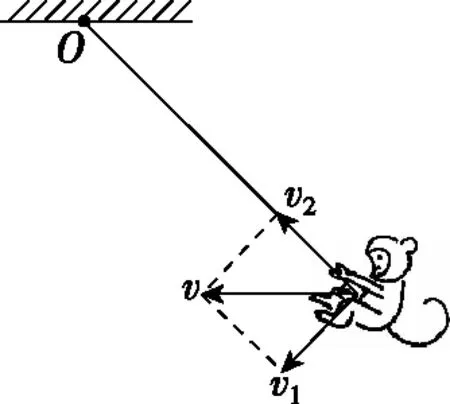
图5

在前面提出的问题中，小船实际沿水面向左的直线运动是小船的合运动，这个合运动可以分解为小船沿绳靠近定滑轮的平动与绕定滑轮的转动。

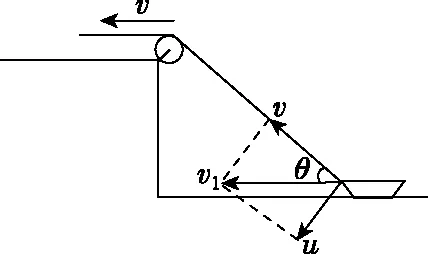
图6

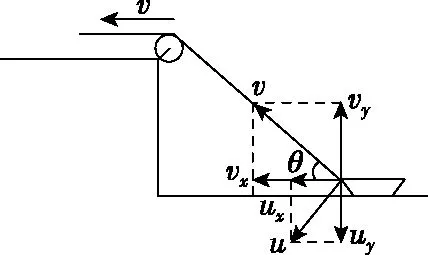
图7

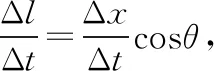
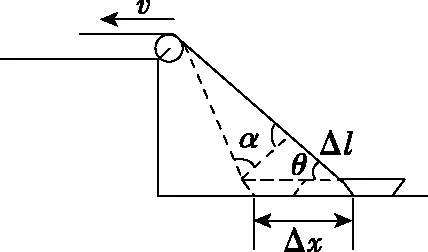
图8

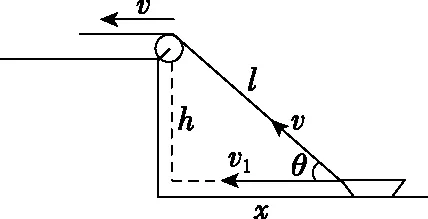
图9

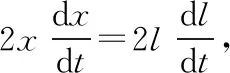
【点评】以上解法1基于小船的合运动与分运动，将合运动按实际产生的分运动效果进行分解，是最容易想到的一种解法。但对于较复杂的牵连体运动，一般不易正确地判断出物体的合运动与分运动导致运动的分解出错；解法2将小船的两种分运动进行再分解，揭示出原错解错因，是一种最具内涵的解法；解法3基于平均速度与瞬时速度的关系，用到了微元法，需要用到数学上的近似计算，这是一种处理变化问题的基本解法；解法4基于速度的物理意义，用到了求导法，通过几何知识找出牵连体运动的位移大小关系，这种解法对数学知识要求较高，但这是一种实用的解法；解法5利用了能量守恒，巧妙地利用牵连体间内力的机械功率关系求解，求解过程简洁，给人一种高屋建瓴之感，是一种最为巧妙的解法。

【小结】对绳、杆牵连物体速度的分析要点

1.先确定合速度的方向(即物体实际运动的方向)。

2.分析合运动所产生的实际效果：一方面使绳或杆伸缩；另一方面使绳或杆转动。

3.确定两个分速度的方向：沿绳或杆方向的分速度和垂直绳或杆方向的分速度。

二、非常规问题分析

(一)动滑轮牵连体

涉及动滑轮的牵连体，因与动滑轮连接物体的运动分解较复杂，求解这种牵连体的速度问题，可以用微元法、求导法、转换参考系法、能量守恒法等方法进行分析与求解。

【例1】如图10所示，物体A置于水平面上，A的前端固定一小动滑轮B，右侧高台上固定一小定滑轮D，一根轻绳一端固定在C点，再绕过两滑轮B、D。其中绳BC段水平，当以速度v0拉绳子自由端时，物体A沿水平面运动，当跨过动滑轮B的两段绳子夹角为α时，物体A运动的速度大小v是多少？

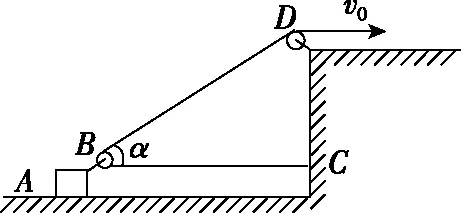
图10

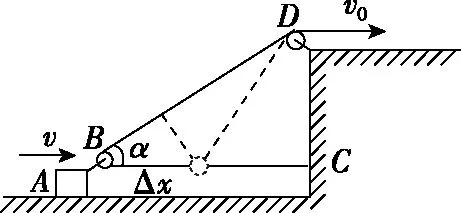
图11

图12

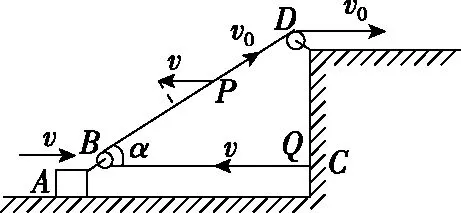
图13

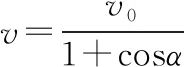
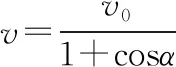
【例2】如图14所示，AA1、BB1是固定于天花板上的两光滑竖直杆。细绳的一端固定在B点，另一端拴在套于AA1杆的珠子D上，另一颗珠子C穿过细绳且套在杆BB1上。已知珠子C以速度v1匀速下落，当细绳与杆AA1成θ时，珠子D上升的速度v2大小为

( )

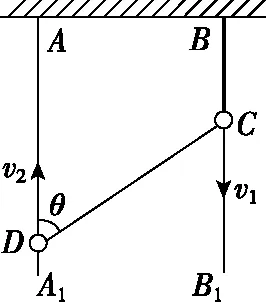
图14

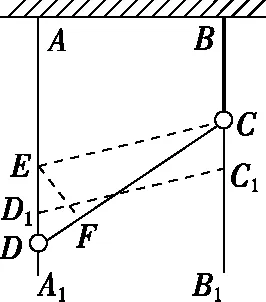
图15

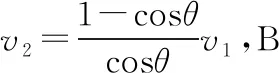
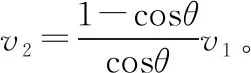
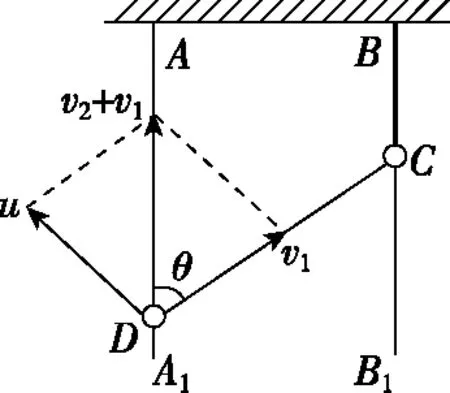
图16

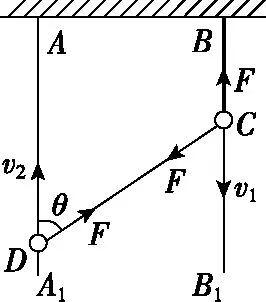
图17

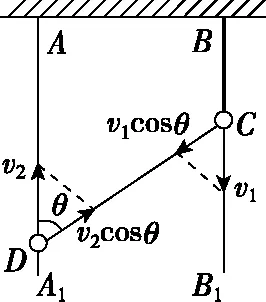
图18

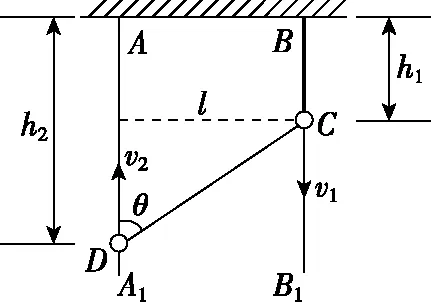
图19

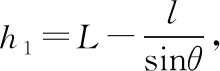
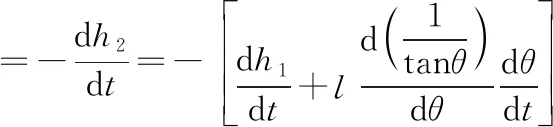
(注：上式求导第一个“-”表示h2在减小)

【点评】例2中的的珠子C相当于动滑轮。对于涉及动滑轮的牵连体速度问题，与动滑轮连接物体的速度分解较复杂，分析求解时可以转换参考系，利用物体相对速度间的关系进行分析求解。微元法与求导法是分析问题的基本方法，能量守恒法是分析求解牵连体速度问题的最巧妙方法。

三、杆连牵连体

杆在运动的同一时刻，杆上各点沿杆方向的分速度相同。利用这一特点，我们可求出某一时刻杆两端点(物体)的速度大小关系。求运动某时刻杆上其他点的速度，也有多种方法，如合成法、分解法、推论法、瞬时转轴法等。

【例3】在光滑的水平面上建立如图20所示的坐标系，一光滑的细杆两端A、B被分别约束在x、y轴上运动。现让A沿x轴以v0的速度匀速运动，已知P为杆的中点，当杆与x轴的夹角为θ时，P点的速度大小为

( )

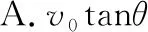
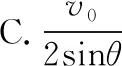
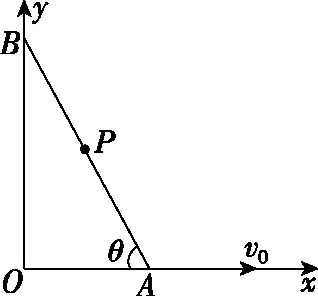
图20

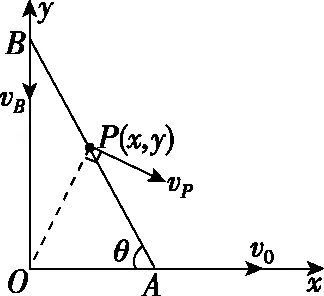
图21

解法1(合成法) 如图21所示。A、B两点沿杆方向的分速度相同，可得vBsinθ=v0cosθ，即vB=v0cotθ

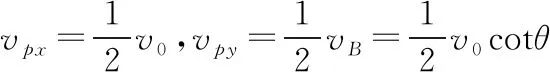
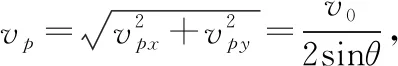
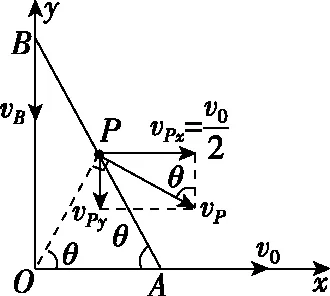
图22

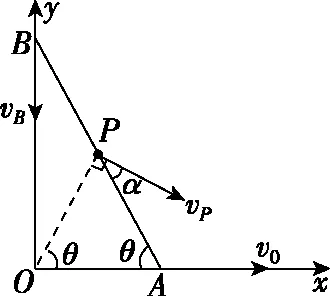
图23

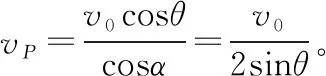
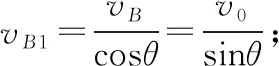
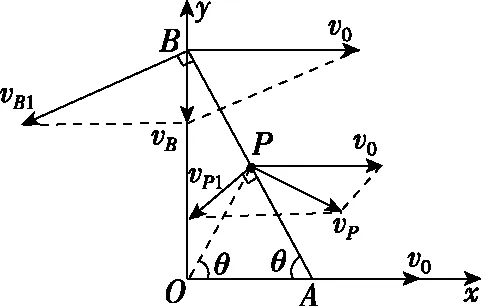
图24

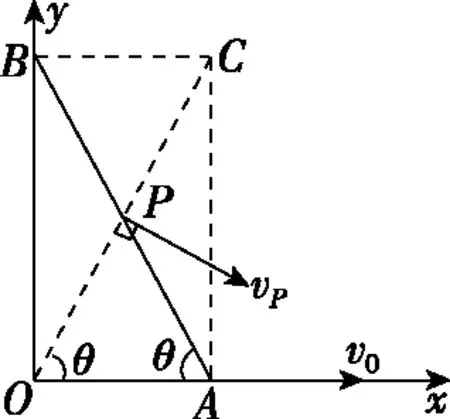
图25

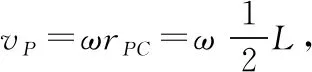
【点评】在以上解法中，解法1先求其水平与竖直分速，然后用勾股定理求其合速度；解法2在解法1的基础上，通过三角函数来求其合速度；这两种解法都是最容易想到的方法；解法3根据P点的速度方向，再利用杆上所有点均有沿杆方向相同的分速度这一推论进行求解，是一种实用的解法；解法4与解法5将杆上所有点的运动分为平动与转动，选取了瞬时转轴，是一种巧妙的解法；瞬时转轴的选取是任意的，解法5中巧妙地选过C点且垂直纸面的轴为瞬时转轴，由于P点的速度vP方向垂直于PC，A点速度v0的方向垂直于AC，求解过程简洁。

总之，关于牵连体速度问题的分析，一般有多种方法。除运动的合成与分解的方法外，还有能量守恒法、微元法、导数法、转换参考系法、相对速度法、瞬时转轴法等特殊方法。