液压型风力发电机低风速下的恒转速控制方法
2021-04-08石青易邓晓刚肖鑫源
石青易 邓晓刚 肖鑫源
(重庆科技学院 机械与动力工程学院, 重庆 401331)
风力发电机组通常采用齿轮箱或整流逆变装置,而这些装置容易出现故障。液压型风力发电机组则具有功重比高、易于实现无级调速等优势。恒转速输出控制问题是液压型风力发电机组面临的关键问题之一。针对风速及载荷扰动的情况,Vaezi等人的研究[1-2]实现了机组系统的恒转速输出控制;Laguna等人的研究[3]是在闭式回路系统中,通过控制系统压力的方法来实现发电机恒转速输出;李飞龙等人的研究[4]是通过改变变量泵排量来控制风力机转速,对马达转速则通过改变其斜盘摆角来控制,从而实现发电机的恒定转速输出。艾超等人[5]基于定量泵-变量马达容积调速系统,提出了一种小信号线性化抗干扰控制方法,实现变量马达恒转速输出。王刚等人[6]针对液压蓄能式风力发电机组的恒转速输出控制问题,提出了基于容积调速与节流调速的复合控制方法。但有关研究未涉及低风速的情况。
本次研究,主要探讨在低风速条件下液压型风力发电机组的恒转速输出控制问题。以大功率低速大扭矩径向柱塞泵代替传统的定量泵,针对定量泵-变量马达闭环系统传动方式,在不同的输入转速条件下,采用PID算法闭环调速控制[7]的方法控制变量马达排量的变化,实现恒速输出,带动同步发电机并网发电。对其主传动控制系统进行了仿真实验,分析了在低风速情况下系统的恒转速控制性能。
1 系统结构与工作原理
定量泵-变量马达液压传动控制系统的工作原理如图1所示。在液压传动控制系统中用变频电机替代风力机。变频电机产生的输入转速,经过减速比为50的减速机减速,控制输入到定量泵的转速范围为5~12 rmin。额定排量为8 800 mLr的定量泵输出稳定的流量,额定压力为11.5 MPa的溢流阀起到一个卸荷安全阀的作用。当系统的压力低于11.5 MPa 时,定量泵输出流量正常流入液压回路。二位四通电磁铁换向阀和液控单向阀共同作用,接通40 mA电流后电磁铁换向阀开始工作,流量进入液控单向阀,当达到单向阀设定的压力值时单向阀开始工作,流量通过单向阀而进入变量马达。此时,转速控制系统会自适应调整变量马达斜盘摆角,使马达输出恒定转速1 500 rmin,带动与其直接相连的同步发电机转动而产生频率稳定的电流。
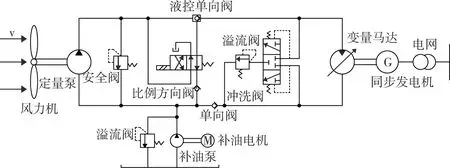
图1 主传动系统工作原理简图
2 数学建模
图2为定量泵-变量马达主传动系统的数学模型简图,相关理论假设参照文献[8]。

图2 数学模型简图
定量泵流量方程为:
Qp=πDpωp1000-Cip(ph-pl)-Cepph
(1)
式中:Qp—— 定量泵流量,Lmin;
Dp—— 定量泵排量,mLr;
ωp—— 定量泵转速,rmin;
Cip—— 定量泵内泄漏系数;
Cep—— 定量泵外泄漏系数;
ph—— 定量泵与变量马达之间的高压管路压力,bar;
pl—— 定量泵与变量马达之间的低压管路压力,MPa。
定量泵的力矩平衡方程为:
Tp-Dpph=Jp(d2θpdt2)+Bp(dθpdt)+Gpθp
(2)
式中:Tp—— 定量泵端的力矩,N·m;
θp—— 定量泵转角,rad;
Jp—— 定量泵轴上的转动惯量,kg·m2;
t—— 定量泵旋转时间,s;
Bp—— 定量泵的阻尼系数;
Gp—— 定量泵端的负载弹簧刚度,Nm。
变量马达排量方程为:
Dm=Kmγ
(3)
式中:Dm—— 变量马达排量,mLr;
Km—— 变量马达排量梯度,mLr;
γ—— 变量马达摆角位置,其取值区间为[0,1]。
变量马达流量方程为:
Qm=Kmγ(dθmdt)1000+Cim(ph-pl)+
Cemph
(4)
式中:Qm—— 变量马达流量,Lmin;
θm—— 变量马达转角,rad;
Cim—— 变量马达内泄漏系数;
Cem—— 变量马达外泄漏系数。
由此,主传动系统高压管路流量的连续性方程为:
Qp=Qm+(Vodph)(βedt)
=Kmγ(dθmdt)1000+Cim(ph-pl)+
Cemph+(Vodph)(βedt)
(5)
式中:Vo—— 主传动控制系统的高压腔内总容积,L;
βe—— 高压油的综合体积弹性模量。
变量马达的力矩平衡方程为:
Kmγ(ph-pl)=Jm(d2θmdt2)+Bm(dθmdt)+Gmθm+Tm
(6)
式中:Tm—— 变量马达轴上的转矩,N·m;
Jm—— 变量马达轴上的转动惯量,kg·m2;
Bm—— 变量马达的阻尼系数;
Gm—— 变量马达端的负载弹簧刚度,Nm。
3 恒转速控制方法
为了使同步发电机产生频率稳定的电流,满足并网发电的要求,采用PID算法闭环调速控制,实现变量马达的恒转速输出。首先利用定量泵轴上的转速传感器测定定量泵转速,然后通过摆角折算系数换算出变量马达摆角基准γ0,将γ0作为执行器的输入控制信号。在此基础上加入PID转速闭环控制,先用转速传感器检测获得变量马达实际输出转速,与给定1 500 rmin恒定马达转速构成偏差,然后利用PID控制器输出变量马达斜盘摆角偏差Δγ,通过计算(γ0-Δγ)得出变量马达斜盘摆角控制值,输入执行器调整变量马达斜盘摆角,使被控对象变量马达转速达到1 500 rmin恒定转速。这样,可避免系统的压力超出工作压力范围而造成系统溢流损失,从而提高系统的稳定性,增强其抗干扰能力。图3为控制流程简图。

图3 恒转速控制流程简图
4 恒转速控制仿真实验
利用AMEsim软件建立主传动控制系统仿真模型,如图4所示。通过改变电动机输入转速而模拟不同风速,通过改变负载溢流阀压力而模拟负载变化,探究在低转速输入(5~12 rmin)情况下,变量马达稳速输出的影响因素和恒转速输出的抗干扰性能。

1 — 电动机; 2 — 转速传感器; 3 — 定量泵; 4 — 溢流阀;5 — 液控单向阀; 6 — 二位四通换向阀; 7 — 单向阀; 8 — 溢流阀;9 — 冲洗阀; 10 — 变量马达; 11 — 转速传感器; 12 — 负载转动惯量;13 — 齿轮传动链; 14 — 定量泵; 15 — 溢流阀
4.1 系统恒转速输出的影响因素
4.1.1 定量泵低转速输入的影响
仿真时,变量马达端负载功率和PID参数保持不变。在给定的定量泵转速5~12 rmin范围内,液压型风力发电机组变量马达转速的变化如图5所示。

图5 不同输入转速下的变量马达转速
对于定量泵的不同转速输入,变量马达输出转速都能够保持1 500 rmin不变,满足转速控制要求。定量泵转速越大,变量马达转速的响应速度越快。
4.1.2 定量泵负载压力的影响
仿真时,低速泵输入转速和PID参数保持不变。在给定的定量泵负载压力0.5~5.0 MPa范围内,液压型风力发电机组变量马达转速的变化如图6所示。
在定量泵转速输入一定的情况下,定量泵负载压力的变化,对变量马达输出转速的影响不明显,变量马达输出转速可以保持1 500 rmin不变。不过,负载压力越大,变量马达转速的响应速度越慢。
4.2 恒转速输出稳定性测试
在液压型风力发电机组实际使用过程中,风速和负载都会随时发变化。为了保证变量马达恒转速输出,产生频率稳定的电能,则需要给风力机和负载施加一个连续变化的信号,模拟实际风速与负载的变化,从而考查控制系统的抗干扰能力。
4.2.1 定量泵转速变化的影响
在定量泵负载压力一定时,调整变频电机,分别施加定量泵转速8~12 rmin斜坡变化、(10+2 sin 0.4πt)rmin正弦变化,得到的系统响应仿真结果如图7和图8所示。

图6 不同负载压力下的变量马达转速

图7 定量泵转速斜坡变化时仿真结果

图8 定量泵转速正弦变化时仿真结果
当风速分别为斜坡变化、正弦变化时,系统输出转速在调速阶段波动较大;当输出转速到达1 500 rmin时,系统输出转速只是在小范围内波动,能够实现稳定控制。同时,在风速变化相同的情况下,负载越大,则转速调整时间越长。
4.2.2 定量泵负载变化的影响
在定量泵转速一定时,给负载压力分别施加40~60 bar斜坡变化、(50+10 sin 0.4πt)/10 MPa正弦变化,得到的系统响应仿真结果如图9和图10所示。

图9 定量泵负载斜坡变化时仿真结果
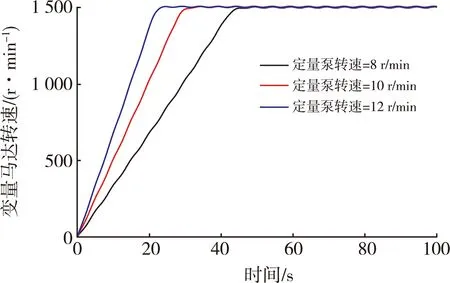
图10 定量泵负载正弦变化时仿真结果
当定量泵负载压力分别为斜坡变化、正弦变化时,系统输出转速依然能够实现恒定控制。同时,在负载变化相同的情况下,风速越大,转速调整所需的时间就越少。
根据仿真测试结果,在风速和负载发生变化时,系统输出转速都可以在很短的时间内实现稳定控制。这表明设计的恒转速输出控制系统的抗干扰能力较强,能够适应风速和负载随时发生变化的实际应用环境。
5 结 语
采用大功率低速大扭矩径向柱塞泵代替传统的定量泵,设计定量泵-变量马达液压传动控制系统,实现液压型风力发电机组在低风速下正常发电,降低其对风速的要求,从而提高对风能的利用率。仿真测试结果表明,在低转速下,定量泵的不同转速输入和不同负载,对变量马达恒定输出转速的影响效果不明显。针对定量泵转速输入的波动和负载的变化,采用PID算法闭环调速控制的方法,在低风速情况下能够有效实现变量马达恒转速输出,系统稳定,抗干扰性能良好。
