因果排除论证:一种因果贝叶斯网络分析
2021-04-08吴东颖朱林蕃
吴东颖,朱林蕃
(复旦大学 哲学学院,上海 200433)
在心灵哲学中,许多接受物理主义的哲学家主张非还原的物理主义。一方面,非还原的物理主义重视心灵属性的独特性与自主性,强调心灵属性有其特殊之处,不能还原为物理现象;另一方面,非还原的物理主义容许心灵因果效力的存在。心灵因果性在心理学与认知科学中已被普遍接受,心理学家与认知科学家认为,心灵现象(例如信念与意图)可以充分解释各种行为与认知现象。在常识语境中,人们也认为心灵属性可以引起人的行为与思考。哲学家认为,非还原的物理主义与上面心理学与认知科学的预设,以及人们的日常常识是兼容的。[1]124-125然而,非还原的物理主义却仍然受到因果排除论证的挑战,这个论证显示心灵属性不具有因果效力。更进一步,亚历克斯·格布哈特(Alex Gebharter)透过计算机科学与统计学的因果测量新兴技术:因果贝叶斯网络(Causal Bayes Net)分析,显示因果排除论证的结论正确。但是排除论证能被因果网络分析吗?是否满足被分析的条件?非还原的物理主义者接受心物随附论。心物随附论的内容是心灵属性随附于物理属性,如果物理实体的心灵属性不一样,那么这个实体的物理属性必然不一样。科学哲学家劳伦斯·夏皮罗(Lawrence Shapiro)、埃利奥特·索伯(Elliott Sober)和詹姆斯·伍德沃德(James Woodward)认为,随附性不能被因果网络分析,但是干预主义能反驳因果排除论证,进一步辩护心灵因果效力。[2,3]那么,随附性究竟可否被因果网络分析?本文将围绕相关问题展开哲学探寻。
一、因果排除论证
(一)非还原的物理主义
非还原的物理主义者主张世界由物理实体组成,这也是被称作物理主义的原因。但进一步认为物理实体可以同时拥有两种不同的属性,即心灵属性与物理属性。非还原的物理主义者普遍认为,心灵属性不可还原为物理属性,心灵属性不在物理领域之内。非还原的物理主义可以兼容多重可实现性(multiple realization),因为心灵属性不等同于物理属性。[1]123-124
非还原的物理主义主张心灵属性具有因果效力。一个属性因果地引起另一个属性,指的是一个属性的例示因果地引起另一个属性的例示。属性的例示则指事件﹑状态或现象。[4]41接受心灵因果效力的理由有二:第一,道德责任以心灵因果效力为前提条件。如果没有心灵因果效力,那么人就无法控制自己的行为,因此没有道德责任。可是我们普遍认为人类有道德责任,所以必定有心灵因果效力。第二,人类的知识也以心灵因果效力为前提条件。例如,外在世界引起人类的知觉经验,进而形成知识。[1]9,[5]
非还原的物理主义者也接受心物随附论。心物随附论预设了心物决定论:任何心灵状态都必然地被某物理状态所决定。换句话说,任何心灵属性都是被某物理属性所实现,而且任何拥有此物理属性的实体必然拥有同样的心灵属性。接受心物随附论的理由是,心物随附论表达了心灵与物理实体之间的共变性,更重要的是心灵对物理实体的依赖性,这是任何一个严肃的物理主义者都接受的基本条件。[6]34
综上所述,金在权(Jaegwon Kim)指出非还原的物理主义可被视为以下四个主张:
1. 实体物理主义:时空世界中只存在物质和物质的聚合物。
2. 心灵的不可还原性:心灵属性不能被还原为物理属性。
3. 心灵因果效力:心灵属性具有因果效力,心灵属性可以引起其他心灵事件或是物理事件。
4. 心物随附论:当一个心灵属性M在某时间点t被某个实体x所例示,是由于x在时间点t也例示了物理属性P,因此在任何时间拥有P都必然地同时拥有M。[1]122-123,[6]33-35
(二)因果排除论证
因果排除论证最早来自于哲学家金在权在1998年和2005年的两本著作。[4]37-47,[6]32-69金在权认为,排除论证最早可追溯于18世纪美国哲学家乔纳森·爱德华(Jonathan Edwards)。[6]36-38因果排除论证接受非还原的物理主义的四个命题,但额外增加两个假设。第一个假设是物理因果封闭原则。
物理因果封闭原则:如果一个物理事件在时间点t有原因,那么这个物理事件在时间点t有一个充分的物理原因。[1]214,[6]43
接受物理因果封闭原则的理由是,物理事件绝不跨越物理和非物理的界线。如果否认这个原则,等于否认一个完备的物理理论存在。换句话说,如果否认物理因果封闭原则,将导致接受任何一个物理领域内的解释都可以诉诸一个非物理领域的原因,而这个结果则不能被严肃的物理主义者所接受。[4]40,[6]43
此外,支持物理因果封闭原则的理由还包括物理学中的能量守恒定律和神经科学发现。能量守恒定律保证了一个系统中总是维持相同的能量总和,任何物体间的交互总是保存同样的能量。这使得物理事件必定有一个充分的物理原因,因为这个物理原因提供了能量交换,而心灵属性在封闭的物理系统中没有空间提供其他多余能量。而这个结果能支持物理因果封闭原则。[7]
其次,物理因果封闭原则不需要预设决定论或非决定论。如果这是非决定论的世界,物理因果封闭原则可以被概率描述,方法为将每一个有原因的物理事件为某一个物理原因所引起的概率固定为1。无论如何,物理因果封闭原则和决定论或非决定论是两个独立的问题。[8]
排除论证的第二个假设是因果排除原则。
因果排除原则:没有任何一个事件在任何一个时间点有两个以上的充分原因,除非这情况是真正的过度决定。[1]216,[6]42
接受因果排除原则的理由是,金在权主张,如果不是过度决定,但是如果有两个原因是完整的对同一个事件的因果解释,那么这两个原因必定不是相互独立的。[9]其次,如果一个原因已传递足够的能量给结果,那么根据能量守恒原则,就不需要另一个原因传递能量给结果。[10]
此外,心物因果似乎不是真正的过度决定。逻辑上,真正的过度决定有可能发生,例如两个枪手同时对同一人开枪,每个枪手的子弹都足以杀死被害人。虽然这种情况是真正的过度决定,但应该不常发生。可是心物因果无处不在,因此,每一次心物因果的发生都刚好是真正过度决定的可能性非常低。如果否认心物因果都是真正的过度决定,那么物理原因就已经完成引起结果的所有工作,已经没有任何空间让心灵原因产生任何结果。[4]52-53
综合以上非还原物理主义与因果排除论证的假设,因果排除论证证明心灵属性不具有因果效力。让M1与M2表示在时间点1与时间点2的心灵属性。让P1与P2表示在时间点1与时间点2的物理属性。这个论证可以图1来表示:[11]355
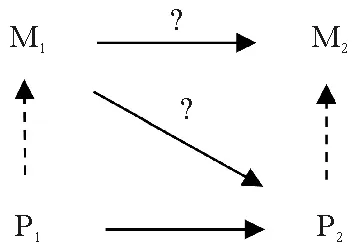
图1 心物因果图
图中,M1与M2是时间先后的两个心灵事件,而P1与P2是分别具现M1与M2的物理事件。P1与P2间的箭头表示因果关系,且根据物理因果原则,P1是导致P2的充分原因。M1与P1间、M2与P2间的虚线箭头表示随附关系。根据随附原则,M1随附于P1,M2随附于P2。M1与P2间、M1与M2间的箭头表示心物因果关系。因果排除论证推论如下:根据心灵的因果效力,M1引起M2。根据心物随附论,P2是M2的随附基础。因为即使M1不发生,只要P2已经发生,那么M2就必然地会发生。所以,M2的发生必定是因为M1和P2产生某种联系。所以M1引起M2是通过P2引起的。现在再次根据心物随附论,P1是M1的随附基础。根据物理因果封闭原则,P1引起P2。但是根据心灵的不可还原性M1≠P1。现在M1引起P2,而且P1也引起P2。假设心物因果确实不是真正的过度决定,那么P2不被M1与P1过度决定。再根据排除原则与物理因果封闭原则,结论是M1被P1所排除。M1不是P2的原因,所以心灵属性不具有因果效力。[1]216-217,[6]41-45
二、因果贝叶斯网络
(一)因果贝叶斯网络简要阐述
因果贝叶斯网络是将贝叶斯主义运用在判断与发现因果关系的新兴研究。简言之,因果网络利用数学工具寻找不同事件或变量之间的变化,建立正确的因果观念,而不同于过去仅盲目寻找各变量的统计相关性。由于因果网络的基础理论部分包括数学公理与概率运算,以下简要举例说明因果网络的两个重点原理。
第一个重点原理是概率独立性。举例说明,〈掷一个硬币得到正面〉不会增加〈掷另一个硬币得到正面〉的概率,因此这两事件是概率独立(指一个事件的发生不会影响另一个事件发生的概率)。相反的,〈火灾〉会增加〈烟雾〉发生的概率,则两事件不是概率独立,即一个事件的发生会影响另一个事件发生的概率。[12]11
第二个重点原理是因果马尔可夫条件(Causal Markov Condition)。如果相信任一有原因的事件X都只由X的直接原因所导致,而且X与X的原因之间是稳定、自主、不变的因果机制,那么理论上只要给定X的直接原因,X的发生概率应独立于所有其他的事件,除了那些被X引起的事件。因果马尔可夫条件的定义是:条件概率P(任一事件X|所有导致X的原因)独立于所有其他不是以X为原因的事件。将事件A发生的概率写作P(A)。将已知A发生的情况下,B发生的概率称之为条件概率(Conditional Probability),写作P(B|A)。假设有三个事件,分别是〈警报〉〈烟雾〉和〈火灾〉,三个事件发生的概率分别是P(警报)、P(烟雾)和P(火灾)。假设〈烟雾〉是引起〈警报〉的原因,〈火灾〉是引起〈烟雾〉的原因。如果三个事件形成的因果网络满足因果马尔可夫条件,而且火灾引起烟雾(以P(烟雾|火灾)的固定值表征)、烟雾引起警报(以P(警报|烟雾)的固定值表征)都是稳定、自主、不变的因果机制,那么三个事件同时发生的概率应是P(火灾)×P(烟雾|火灾)×P(警报|烟雾),而不是P(警报)×P(烟雾)×P(火灾)。因为后者错误地预设三个事件彼此概率独立,但P(烟雾|火灾)显然大于P(烟雾),因为若有火灾发生,则有烟雾发生的概率显然大得多。[12]23-26
如果一个自然现象满足以上两个重点原理及其他相关原理(篇幅限制不全部列举),则可绘制因果图(Causal Diagrams)来表征此自然现象的因果关系,并利用因果图做更容易理解和利用的因果推理。因果图由节点和箭头组合而成:节点表示某一事件的发生与否,例如〈警报〉〈烟雾〉和〈火灾〉;箭头表示因果关系。从〈火灾〉和〈烟雾〉间,与〈烟雾〉和〈警报〉间,各画一个箭头,表示各两事件之间有因果关系。因此,〈警报〉〈烟雾〉和〈火灾〉三个事件的因果图为:“火灾→烟雾→警报”。[12]14
因果图的优点是易于理解且能预测概率独立关系。例如,〈烟雾〉和〈警报〉概率不独立,〈火灾〉和〈烟雾〉也概率不独立。因为根据因果图,这些事件之间有箭头存在(表示有因果关系)。但假设已经有〈烟雾〉,则〈警报〉和〈火灾〉两事件变成条件概率独立,因为〈烟雾〉单独决定是否有〈警报〉。因为,就算没有〈火灾〉,只要有〈烟雾〉(例如炒菜油烟雾),仍然会有〈警报〉。而且根据因果图,〈警报〉和〈火灾〉无箭头,表示没有直接因果关系。换句话说,〈烟雾〉屏蔽了〈火灾〉至〈警报〉的因果效力。相反的,如果检视所有“有烟雾”的可能情形,发现〈警报〉和〈火灾〉两事件概率不独立,则可以推论〈警报〉和〈火灾〉有直接因果关系,因果图应修正为:“火灾→烟雾→警报←火灾”。因此,因果图可以藉由各事件间概率独立关系,判断事件之间的因果关系。[12]12-26
在因果网络的分析下,透过心灵与身体间因果图的绘制,能重新检视上述的排除论证。
(二)格布哈特对排除论证的辩护
格布哈特针对排除论证的辩护诉诸因果贝叶斯网络。[11]353与条件概率独立性概念相对的是条件概率依赖性概念。让“Dep(X,Y|Z)”代表“条件化Z时,X与Y概率依赖”,让“Indep(X,Y|Z)”代表“条件化Z时,X与Y概率独立”,这两个概念的概率定义如下:
Dep(X, Y|Z)=defP(X|Y, Z)≠P(X|Z)∧P(Y, Z)>0
Indep(X, Y|Z)=defP(X|Y, Z)=P(X|Z)∨P(Y, Z)=0[11]357
其中P(Y, Z)=0时,表示Y与Z不同时发生,所以条件化Z时,X与Z必定互相概率独立。所以因果马尔可夫条件蕴含:给定一个事件X的直接原因,X将条件概率独立于所有不是X引起的事件。这个蕴含等价为:如果给定一个事件X的直接原因(除去Y),X不条件概率独立于某个事件Y,那么Y是X的直接原因之一。(1)这个蕴含必须加上“最小假设”:一个包含了因果图G和概率分布P的因果网络满足最小假设,当且仅当,任何一个较G的箭头少的因果图都无法满足P。由于篇幅有限,本文不再赘述。换句话说,因果马尔可夫条件的蕴含结果可以作为两个事件X与Y之间是否有因果关系的测试标准。让Par(X)代表X的直接原因集。称此测试标准为生产力测试(Productivity test),这个测试标准的定义如下:
生产力测试:对于一个因果网络中的所有变量集V来说,对于所有属于变量集V中的Xj与Xi,而且Xi是Xj的原因,Dep(Xj, Xi| Par(Xj)
生产力测试的优势是能运用各事件之间的条件概率关系,判断各事件之间是否具有因果关系。这个测试必须预设这些事件之间满足因果马尔可夫条件,但是排除论证中不仅有因果关系,还有随附关系。所以是否能运用生产力测试在排除论证,似乎有问题。
但格布哈特进一步论证,可以将随附关系视为某种稳定的因果关系。首先,随附关系与因果关系一样,都具有稳定性(指在背景条件变化的情形下,随附关系或因果关系仍能持续成立)。因为给定P1,M1必然发生,所以P(M1|P1)=1。不论背景条件,包括先验概率P(M1)与P(P1)如何变化,条件概率P(M1|P1)都会等于1,所以具有稳定性。其次,因为给定M1,P1不必然发生,所以P(P1|M1)≠1。这个表征也符合多重可实现性。因为给定一个心灵状态M1,M1不一定被P1所实现,也有可能是其他实现M1的物理属性,所以P(P1|M1)必须在0与1之间。最后,微观性质经常被理解为宏观性质的原因。例如,容器内气体的温度是被容器内气体分子的运动所引起的。因此,可以将因果排除论证中的随附关系视为因果关系。[11]359-361(2)另外,伍德沃德反对将随附性纳入因果网络分析,因为这将导致不好的结果,也违反实务上的实验操作。格布哈特则否认因果网络分析有不好的结果,而且也符合实务。由于本文不采纳伍德沃德的见解,所以不再赘述。参见文末参考文献[11]第369-372页。
如果以上假设与定义正确,格布哈特就能利用因果排除论证的上述假设,以及生产力测试,来确认心灵因果效力。(3)格布哈特并非依照原本因果排除论证的推论步骤得出心灵属性无因果效力,而是直接利用因果排除原则的其中一些假设,搭配生产力测试,得到心灵属性无因果效力的结论。无过度决定已包括在生产力测试与因果网络的最小假设中:M1如果有因果效力,至少要能对P2与M2的概率分配有影响的空间。参见文末参考文献[13]。首先确认P1与P2之间是否有因果关系。根据生产力测试,如果Dep(P2,M1|Par(P2)
格布哈特的论证利用因果贝叶斯网络,主张心灵属性不具有因果效力,进一步为排除论证提供全新的辩护。因果网络仅能精准地以概率相关性的判断方式,确认事件之间是否具备因果关系。笔者将在下节指出格布哈特的论证仍有缺陷。
三、随附性与因果贝叶斯网络
如上所述,因果贝叶斯网络的运用必须满足因果马尔可夫条件,而格布哈特预设排除论证满足因果马尔可夫条件,所以能利用因果网络的生产力测试来决定心灵属性的因果效力。但因果排除论证能否满足因果马尔可夫条件,关键在于是否能将随附性视为因果性的一种。格布哈特认为基于随附性的几项特征,能将随附性视为因果性以因果贝叶斯网络分析。实际上,随附性仍有其他特征,似乎不适合将随附性作为因果性以因果贝叶斯网络分析。
首先,随附性与因果性的模态与逻辑属性不同,所以似乎不能将随附性视为因果性的一种。随附性与因果性有不同的模态性。心物随附论的模态强度是形上学必然的。[13](4)心物随附论的强随附关系的模态强度是形上学必然的有争议。有哲学家主张,物理主义者必须允许心物随附论的模态强度是形上学必然。参见文末参考文献[14]。如果某个实体具有物理属性P1,那么形上学上必然的有M1。但是因果性的模态强度是形上学偶然的,如果P1引起P2,那么形上学上有可能P1不引起P2。所以随附性不是因果性。
其次,随附性具有自反性,换言之,所有的东西都可以随附于自己:即X随附于X,因为如果X不一样,那么X一定不一样。相反,因果性通常不具有自反性,换言之,通常一个事物不能因果地推导出自身。因为随附性具有自反性,但因果性不具有自反性,所以不能将随附性视为因果性。
另外,排除论证的提出者金在权已经澄清随附性与因果性不同。如果A随附于B,那么A与B在时空上是重叠的。相反的,如果A因果引起B,那么A与B则不能在时空上重叠。[4]18更进一步,如果A随附于B,那么A与B是同时发生的。相对的,如果A因果引起B,那么因为原因一定早于结果,所以A与B则不是同时的。[1]36基于时空重叠性与时间性的考察,不能将随附性直接视为因果性。
将随附性纳入因果贝叶斯网络分析至少还有一个形式表征问题。假设引起P1的物理属性是P0,而且引起M1的物理属性包括P1,那么引起M1的物理属性包括P0,所以P0是P1与M1的共同原因。但因果贝叶斯网络通常假设因果充分原则,即因果图中所有变量的共同原因都必须纳入因果图内,所以必须考虑P0。[15]根据生产力测试,如果P1是M1的原因,那么P(M1|P1, Par(M1)) ≠ P(M1|Par(M1))。但是因为Par(M1)包括P0,而且P(P1|P0)=1,因此P(M1|P1, Par(M1))= P(M1|Par(M1))。所以P1不是M1的原因,这违反格布哈特将P1与M1之间视为因果关系分析的假设。如果要避免这个结论,格布哈特必须要先验否定P0不是M1的原因,但似乎无法先验论证P0不是M1的原因。
综上所述,随附性与因果性有显著的不同。在排除论证中,心灵属性与物理属性显然具有同时性与时空区域重叠,而且不具有自反性与传递性的决定性关系。这种关系显然不能被视作因果关系。而且将随附性作为因果性的数学值纳入因果网络分析,也可能会遭遇形式表征上的困难。如果仍将其视为因果关系,则令人怀疑格布哈特辩护的对象是否仍是心灵属性与物理属性。
更进一步的,如果不能将心灵属性与物理属性间的关系视为因果关系,那么整个因果排除论证已经不满足因果马尔可夫条件,无法使用因果贝叶斯网络分析。根据因果马尔可夫条件,给定一个变量X的直接原因,那么X与所有不是X的效果条件概率独立。但是根据心物随附论,给定M1时,P1发生的条件概率,较P1独自发生的非条件概率大。而且,给定P1时,M1发生的条件概率为百分之百,因为物理属性决定心灵属性。所以,M1与P1两者之间不存在概率独立关系。
然而,根据因果马尔可夫条件,给定M1的直接原因时,M1必须与“不被M1影响的事件”两者之间具有条件概率独立关系。但P1既不是M1的直接原因,也不是M1的效果,因为M1与P1之间是随附关系,不是因果关系。所以,因果马尔可夫条件蕴含M1必须与P1条件概率独立。但根据心物随附论,M1与P1的概率并非相互独立,所以违反因果马尔可夫条件。
同样的,根据因果马尔可夫条件,给定P1的直接原因时,P1必须与“不被P1影响的事件”之间具有条件概率独立关系。但M1既不是P1的直接原因,也不是P1的效果,因为M1与P1两者之间是随附关系,而不是因果关系。所以,因果马尔可夫条件蕴含P1必须与M1条件概率独立。但根据心物随附论,M1与P1两者的概率并非相互独立。所以,从两个角度看,排除论证中违反因果马尔可夫条件,不能以因果贝叶斯网络分析。所以此处的结论是格布哈特的辩护诉诸了不成立的前提假设。
四、结论
通过对因果排除论证的分析,我们可以看到随附性可能引发排斥因果网络分析的后果。然而,格布哈特的辩护引发了很多哲学争议。例如科学哲学家伍德沃德质疑,同样以因果贝叶斯网络为基础的干预主义,如果不控制具有随附关系的事件,就不会蕴含心灵属性没有因果效力的结果。[2,16,17]科学哲学家弗雷德里克·埃伯哈特(Frederick Eberhardt)也主张,如果因果系统中包含具有构成性(constitutive)等类似随附关系的事件时,在模型建立与变量选择上应避免将这类事件放入因果网络中,而是选择能简单干预且产生简单因果关系的事件来分析。[18]无论如何,目前格布哈特的辩护已使哲学界产生激烈的回响与思辨。
