基于一步法层析速度建模方法建立

徐嘉亮，张冰，王维红，石颖

东北石油大学地球科学学院， 大庆 163318

0 引言

对于日趋复杂的勘探环境，叠前深度偏移是解决复杂构造成像最为有效的手段.深度域偏移速度模型的建立是叠前深度偏移的重点和难点，它的精度直接决定偏移成像的质量(任婷等，2020).DIX(1955)最早利用叠加速度转化为深度域层速度，DIX公式是建立在水平层状介质及速度横向均匀介质基础上的，所以对于真实复杂地质构造，该方法误差较大，但该方法开创了层速度场模型建立的先河.Landa等(1991)提出了一种利用CMP道集进行层析速度建模的方法，该方法不以双曲近似或者叠前旅行时拾取为基础，而是通过射线追踪正演的方法得到旅行时曲线，这种方法完全由地震数据进行驱动，开辟了层速度场建模的全新思路.蒋先勇(2005)对速度建模的影响因素进行了系统的分析.目前工业界经常使用两种层析速度建模方法为深度聚焦分析方法和剩余曲率分析方法，其中剩余曲率分析方法应用最为广泛(Mackay and Abma，1993)，Al-Yahya(1989)基于偏移后的共偏移距域道集拉平准则建立了剩余时差层析速度建模方法，这种方法最先应用偏移结果对速度模型进行有效更新迭代.在此基础之上，Lee和Zhang(1992)提出了带有倾角校正的剩余曲率迭代公式，从而将水平层状介质推广到带有小倾角的地层.Prucha等(1999)、Rickett和Save(2002)、 Sava和Fomel(2003)对角度域共成像点道集的动力学和运动学特征进行了分析，用角度域共成像点道集进行深度域层速度模型迭代更新，从而将层析速度建模的精度推向了新的高度.陈国金等(2006)提出了一种利用速度差异进行层析速度建模的方法，并对成像质量进行了系统的分析.刘守伟等(2007)将剩余曲率分析与深度聚焦分析结合起来，并将其统一到时空域成像条件的时移角度域共成像点道集进行速度分析，该道集携带了地震数据不同入射角信息和不同成像的信息，更有利于速度模型的迭代.徐嘉亮等(2015，2018)、管文胜等(2017)对角道集相对于剩余速度的敏感性进行了分析，得出利用偏大的初始速度进行剩余速度分析效率更高的结论，从而有效解决了层析速度建模计算周期长的问题.以上剩余曲率分析方法都需要提取显式剩余时差，既零偏移距地震道与非零偏移距地震道的垂直距离，利用显式剩余时差建立层析反演目标泛函(吕振宇和魏鹏，2020；张志军等，2020).但是当偏移速度不等于真实速度时，零偏移距地震道不在地层真实的反射界面，而是在真实反射界面的上方或下方，显式剩余时差往往不能表征偏移道集真正的剩余曲率，零偏移地震道与真实反射界面的垂直距离存在隐式剩余时差，隐式剩余时差只能通过显式剩余时差的不断校正所展现.本文提出一种求取隐式剩余时差的方法，利用隐式剩余时差构建层析反演关系，建立一步法层析成像速度建模方法.通过模型数据试算及实际数据应用证明本文提出的一步法层析成像方法是有效可行的，该方法在保证层速度场建模精度的同时能够大幅提高计算效率.

1 算法建立

常规层析成像方法提取显式剩余时差，既零偏移距地震道与非零偏移距地震道的垂直距离，该方法往往忽略了隐式剩余时差的存在，只能通过迭代更新逐步揭示隐式剩余时差，直到迭代更新多次后，偏移道集被拉平，层速度迭代更新充分，如图1所示.

由分析可知，显式剩余时差与隐式剩余时差之和为最大偏移距初始地震道与拉平地震道的垂直距离，如图2所示.通过建立显式剩余时差与隐式剩余时差的关系，即能够对隐式剩余时差进行求取.

假设在深度Z0有一水平层状反射界面，当偏移速度小于地层真速度时，地层偏移深度为Zw，真实局部层速度为V0，地表观测偏移距为h0，零偏移距双程走时为t0，当波场向下延拓时，由于真速度场与偏移速度场有差别，从而产生局部偏移距h，局部偏移距观测系统如图3所示.

常规时距关系式为：

(1)

V1为剩余速度，当利用比真实速度偏大的偏移速度进行波场延拓时，上述关系式可表示为：

(2)

式(2)变形可得：

(3)

因为成像深度不随地表偏移距变化，式(3)对h0进行求导公式依然成立：

(4)

把式(4)代入式(3)中可得：

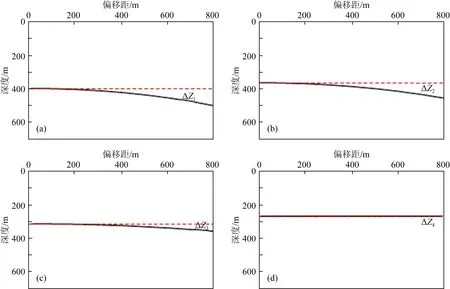
图1 常规剩余时差层析成像(a) 1次更新； (b) 2次更新； (c) 3次更新； (d) 4次更新.Fig.1 Conventional residual time difference tomography(a) First update； (b) Second update； (c) Third update； (d) Fourth update.

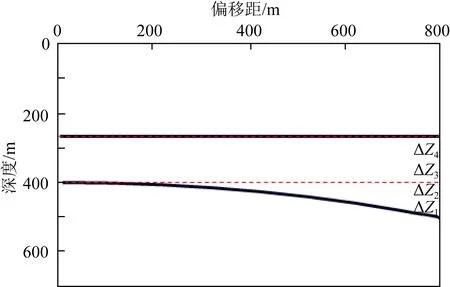
图2 隐式剩余时差Fig.2 Implicit residual time difference

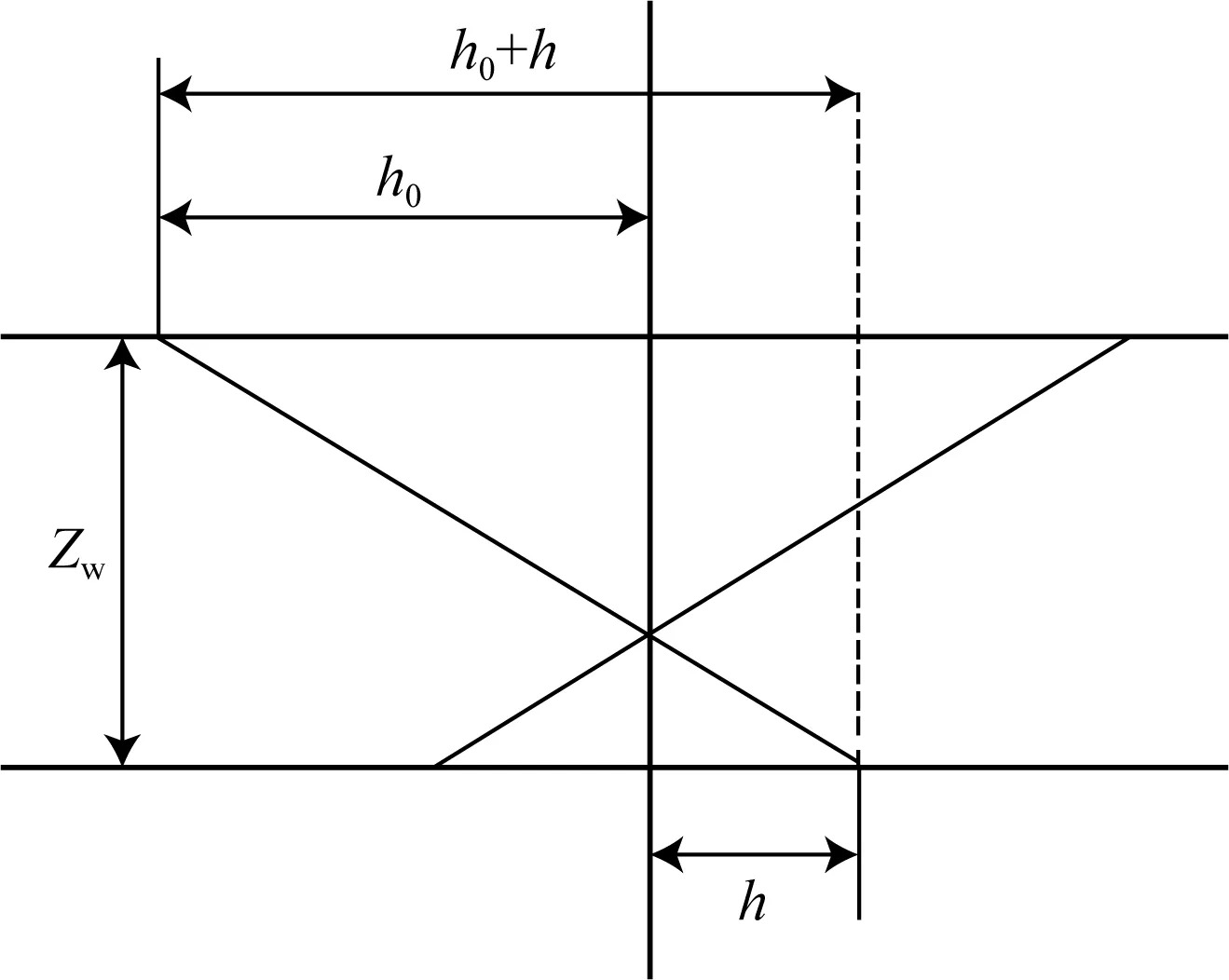
图3 局部偏移距观测系统Fig.3 Local observation system of migration offset

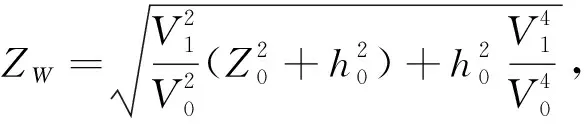
(5)

ΔZ1为显式剩余时差：

(6)

式(6)是以显式剩余时差为自变量，剩余速度为目标函数的关系式.对于零偏移距道集，偏移速度与偏移深度的关系式为：

(7)

令ΔZ2为隐式剩余时差：

(8)

把式(8)代入式(6)，可得显式剩余时差与隐式剩余时差之间的关系：

(9)

本文提出真正剩余时差为显式剩余时差与隐式剩余时差之和：

ΔZ=ΔZ1+ΔZ2，

(10)

结合式(6)、式(7)和式(10)可得以真正剩余时差为自变量，剩余速度为目标函数的关系式：

(11)

结合式(6)和式(9)可以对隐式剩余时差进行定量求取，利用定量求取的隐式剩余时差与显式剩余时差可以对层速度进行速度校正.

2 模型试算

本文以四层层状介质模型进行方法测试，数据正演采用波动方程傅里叶有限差分方法，模型大小为1000 m×1000 m，共100炮，炮间距为5 m，共61个检波点，检波点间距为5 m，子波采用雷克子波，主频为30 Hz，网格大小为3 m×3 m.正演速度模型如图4所示，正演单炮记录如图5所示.四层层速度分别为2000 m·s-1、3000 m·s-1、4000 m·s-1、5000 m·s-1.

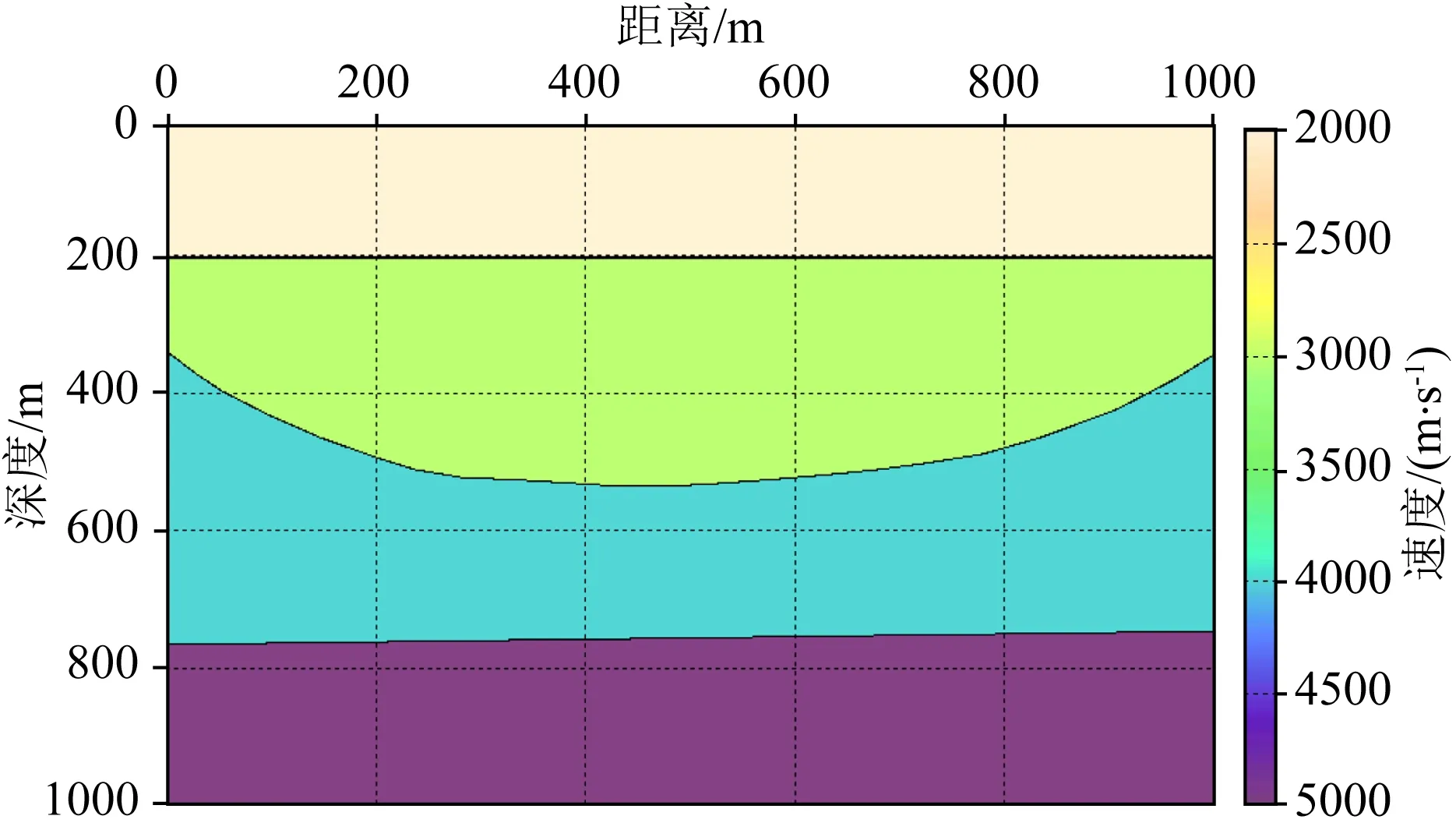
图4 正演速度模型Fig.4 Forward velocity model

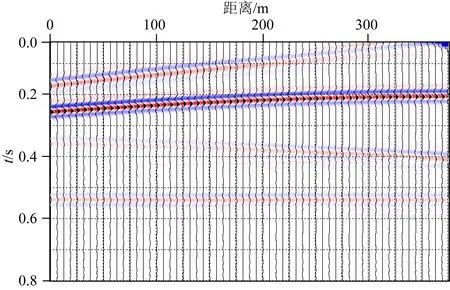
图5 单炮记录Fig.5 Single shot recording

本文以第二层小倾角地层模型层速度为目标层段进行本文方法的测试，首先将第二层速度由3000 m·s-1调小为2500 m·s-1，利用该速度进行叠前深度偏移，偏移后的共反射点道集如图6a所示.因为第二层速度相比真实层速度偏小，第二层与第三层对应的同向轴上翘.

利用常规剩余曲率层析成像方法与本文提出的一步法层析方法分别进行一次层析成像，更新后的共反射点道集如图6b、c所示.利用常规层析成像方法迭代一次后第二层与第三层对应的同向轴仍然存在剩余曲率，说明更新后的层速度模型仍然存在速度误差.利用本文提出的方法更新后的共反射点道集同向轴为水平的直线，说明层速度模型更新完全.

分别利用常规剩余曲率层析成像方法与本文提出的方法进行一次层析迭代，迭代后的层速度模型如图7a、b所示.利用常规层析成像方法迭代一次的层速度(2745 m·s-1)与真实速度(3000 m·s-1)有较大差别.利用本文提出的方法更新后的第二层速度值为2986 m·s-1，与真实层速度值误差为14 m·s-1，该误差对于偏移成像环节可以忽略.

3 实际数据应用

本文以渤海M区块三维地震资料为靶区进行新方法测试，该区块地质条件复杂，低速泥岩广泛发育.该区地震资料品质较好，信噪比较高，适于本文方法的应用测试. 图8a为利用常规层析方法迭代三次速度模型的结果，速度模型的迭代更新共计需要144 h，图8b为本文提出的一步法层析成像方法的速度模型更新结果，由于新方法仅需要一次速度模型的更新，计算时间为36 h.图8c为速度模型抽取的围井速度曲线与实钻声波测井速度曲线的比较.由图8a、b的比较中可知，常规方法速度建模的结果在低速泥岩层段没有响应，利用本文提出方法得到的速度模型在低速泥岩层段有非常好的响应特征，同时速度模型更加平滑.由抽取的围井速度曲线与实钻声波测井曲线的比较中可看出，常规方法速度建模的结果与实钻声波测井速度仍有较大偏差.利用本文提出方法得到的速度模型与实钻声波测井速度吻合度更好，从而证明利用本文提出的一步法层析成像方法建模精度更高，建模效果更高.

图9为利用常规方法及本文提出方法速度建模结果偏移得到的偏移距域共成像点道集，常规方法得到的偏移道集在中远偏移距不够聚焦，并且存在较大剩余时差，由于速度误差导致的偏移假象大量存在.利用本文提出方法得到的偏移道集在中远偏移距较平直，剩余时差较小，偏移道集的信噪比及分辨率更高.

4 结论

本文由剩余时差拾取机理出发，提出隐式剩余时差概念，并建立隐式剩余时差与剩余速度之间的函数关系，利用该关系通过一次计算就可以对剩余速度进行精确求取并对速度模型进行精确更新，避免了常规层析方法需要多次迭代的流程.由模型数据测试及实际数据应用证明，本文提出方法是有效可行的，该方法与常规层析方法进行比较，在大幅提高层速度场建模精度的同时有效减少计算周期，为后续偏移成像节省大量时间.

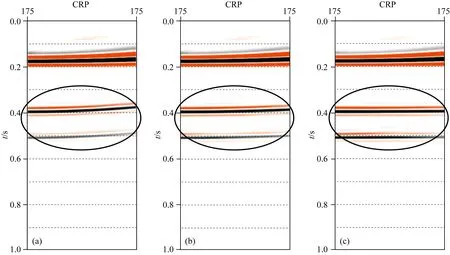
图6 (a) 初始速度模型； (b) 常规方法； (c) 本文方法Fig.6 (a) Initial velocity model； (b) Conventional method； (c) Our method

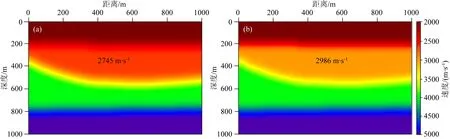
图7 (a)常规方法； (b) 本文方法Fig.7 (a) Conventional method； (b) Our method

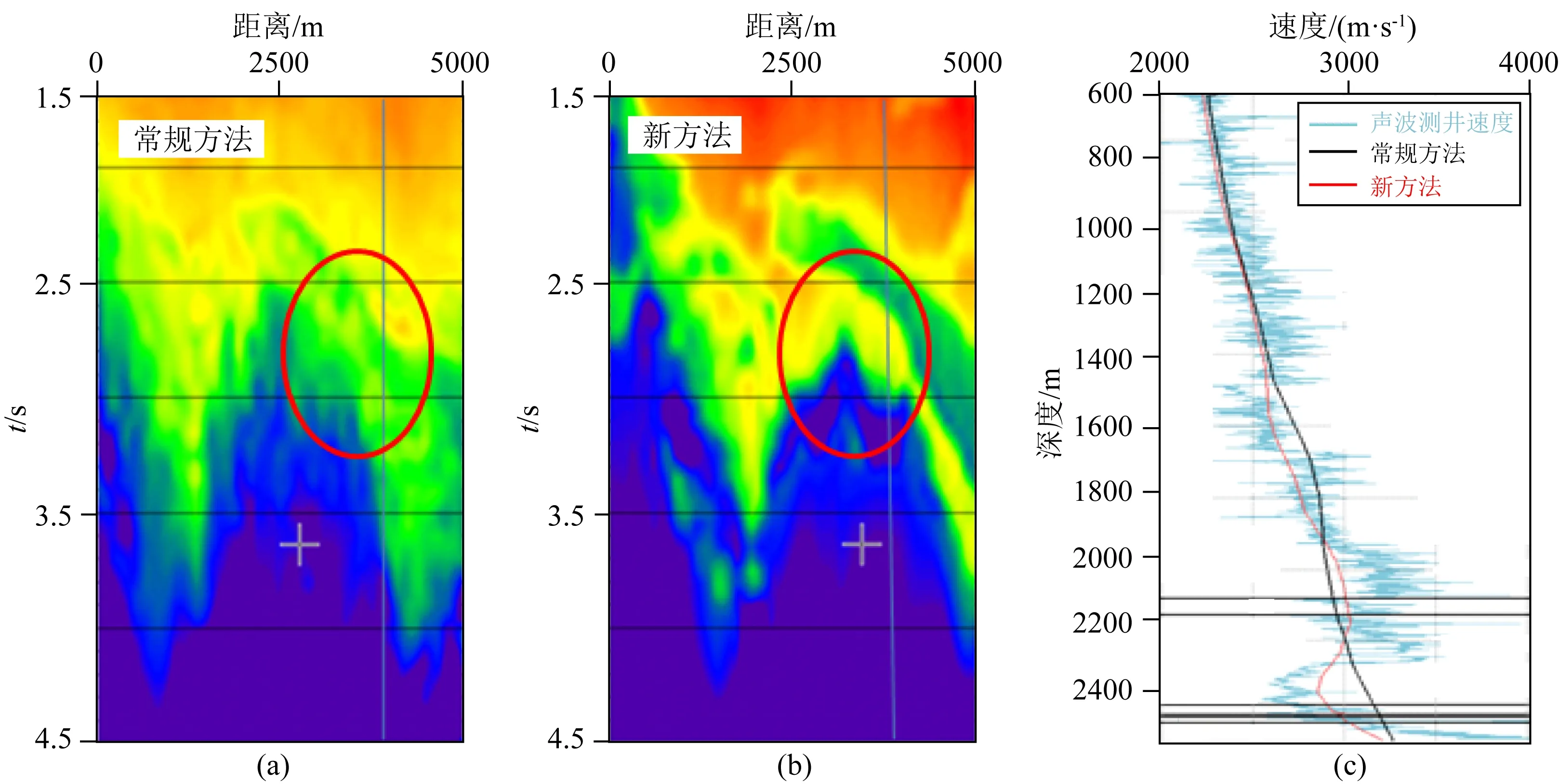
图8 (a) 常规层析方法速度建模结果； (b) 本文提出方法速度建模结果； (c) 抽取围井速度曲线与实钻声波测井速度曲线比较Fig.8 (a) Velocity modeling results by conventional tomography； (b) Velocity modeling results by new method； (c) Comparison of velocity curves of extractive circum-well and acoustic logging in real drilling

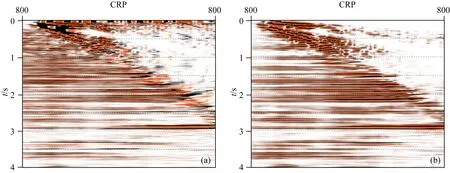
图9 (a) 常规层析方法偏移道集; (b) 本文方法偏移道集Fig.9 (a) Migration gathers by conventional tomography method; (b) Migration gathers by new method

目前很多地球物理应用领域都需要在最短的时间内建立高精度的层速度模型，例如孔隙压力预测问题、波动方程叠前深度偏移问题、全波形反演初始速度模型建立问题等等.利用本文提出的方法可以在保证速度建模精度的同时有效减少计算周期，从而对以上提及的诸多地球物理问题都具有重大且深远的意义.