基于改进蝙蝠算法的风蓄联合优化运行研究

王毛毛，姚景泽，罗清乘，孙佳星

(1.国网襄阳供电公司，湖北 襄阳 441000；2.国网晋中供电公司，山西 晋中 030600)

随着全球新能源的快速发展，风电的大规模开发也越来越受重视。由于风电的波动性和不确定性，大规模并网将对电力系统稳定运行产生一定的冲击。抽水蓄能电站是一种具有启停灵活、反应迅速的储能装置，目前已广泛应用于电力系统，将风电和抽水蓄能电站联合运行，可有效降低风电并网局限性，提高风电运行效益，有关学者进行了深入研究，文献[1]建立了风电-抽水蓄能联合运行的数学模型，并对6种场景进行了仿真分析；文献[2]考虑负荷需求建立了以最大化平滑负荷为目标的风蓄联合优化运行策略。近年来为解决风蓄联合优化运行问题，学者们引进了较多的智能算法，文献[3]首先建立了风蓄联合系统优化运行，通过粒子群算法进行优化求解分析；文献[4]计及碳减排效益，以发电成本最小为目标，建立了风光火电源规划模型，利用蚁群算法进行了仿真分析；文献[5]以风电成本最小为目标，针对风能并网调度问题采用蝙蝠算法进行仿真，仿真表明该算法可以有效解决电网优化调度问题。本文在相关研究的基础上，将佳点集方法引入蝙蝠算法，提出一种改进的蝙蝠算法，将改进蝙蝠算法应用于风电-抽水蓄能联合运行中。

1 数学模型

风电并网的局限性主要体现在输出功率的波动性和随机性，有效评估风电的输出功率对于提升风电的运行效益至关重要，标准差的定义为样本偏离数据平均值的程度，可有效反映数据的波动情况。因此，本文采用标准差来评估风电的输出功率波动情况。

1.1 目标函数

本文采用的调度周期T为24个时段(T=24)，任意时段用t表示，传统风电场单独运行时，引入上述标准差为衡量输出功率波动指标，风电场输出波动标准差为

(1)

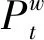
根据每个时段内的输出功率来确定调度周期内的平均输出功率：

(2)

风电出力约束：

(3)

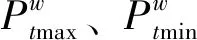
本文将风电和抽水蓄能电站联合运行，已知风电各时段输出功率，以风蓄联合系统输出功率标准差最小建立目标函数：

(4)

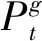
1.2 约束条件

功率平衡约束，风蓄联合系统各机组出力功率应平衡:

(5)

根据风蓄联合系统各机组出力可计算系统出力平均值：

(6)

风电出力约束，风电出力应在上下限区间内：

(7)

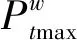
风蓄联合系统出力约束，风蓄联合系统出力应在上下限区间内：

(8)

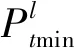
抽蓄电站机组台数平衡约束，t时段抽水工况机组、发电工况机组以及停机机组的总台数为恒定值不变：

(9)

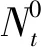
抽水蓄能电站发电功率约束，机组出力应在上下限区间内：

(10)

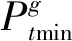
抽水蓄能电站机组抽水功率约束，机组抽水出力应在上下限区间内：

(11)

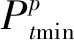
抽水蓄能电站机组抽水和发电互斥约束，机组不能同时处于抽水和发电工况：

(12)

抽水蓄能电站上水库储能平衡约束，下个时段的上水库储能应为本时段的上水库储能与抽水、发电机组储能之和：

(13)

式中：ηp表示机组抽水效率。

抽水蓄能电站上水库储能上下限约束：

Emin≤Et≤Emax

(14)

式中：Emax表示上水库储能上限。

抽水蓄能电站上水库储能变化量约束，考虑到上水库的需水量，在调度周期内，上水库库容的变化量应在一定的裕度内：

|Ee-E0|≤εE

(15)

式中：E0表示调度周期内起始时段上水库储能；Ee表示末尾时段上水库储能；εE表示上水库储能变化量。

2 模型求解

剑桥大学学者YANG X通过研究蝙蝠捕猎的生物学原理提出一种新型全局优化算法，即蝙蝠算法(Bat Algorithm，BA)[6]，该算法主要模拟蝙蝠回声定位捕猎过程，有着参数动态控制、自动缩放等突出优点，一经提出便得到大幅推广，并成功应用于神经网络[7]、模糊聚类[8]、电力系统[9]等方面。

2.1 蝙蝠算法

蝙蝠捕食过程主要通过发射并接收从物体反射回的超声波，以此回声完成识别猎物，这种原理即普勒效应回声定位原理。研究人员模拟蝙蝠捕食时不断识别物体并最终定位猎物的过程，研究出了蝙蝠算法，该算法在搜索前期不断更新速度、频率、位置，迭代生成全局优解，在此基础上进行局部寻优，从而实现了全局寻优和局部寻优密切合作，且在寻优过程中，根据反馈的信息，脉冲响度和脉冲发射率不断更新，使算法一方面寻优速度较快，另一方面寻优精度更加精确。

2.1.1 蝙蝠的速度与位置更新方式

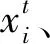
(16)

(17)

该蝙蝠发射频率fi更新公式如下：

fi=fmin+(fmax-fmin)β

(18)

式中：fi为超声波频率，fmin、fmax分别为频率最小值、最大值，fi∈[fmin,fmax]；β∈[0，1]的随机数；x*为t时刻全局最优解。

生成全局最优解后，在这个最优解临近区域随机生成局部新解，更新公式如下：

xnew=xold+εAt

(19)

式中：ε∈[0,1]的随机数，At为当代蝙蝠个体的响度平均值。

2.1.2 蝙蝠的脉冲响度和发射频率更新方式

蝙蝠根据物体的位置不断更新脉冲响度和发射频率来精准定位猎物，基于以上特性，在蝙蝠算法中，通过不断更新脉冲响度At和发射率ri，以此实现算法搜寻过程中全局和局部的平衡。具体表现为，在搜寻接近最优解时，算法的脉冲响度Ai不断减小，发射率ri不断增大，公式表示为

(20)

(21)

式中：响度衰减系数α∈(0,1)；频率增加系数γ>0。

2.2 改进蝙蝠算法

蝙蝠算法在搜寻前期便开始全局和局部搜寻，因此具备较快的寻优速度，然而蝙蝠算法的初始种群是随机选取的，往往分布并不均匀，很难遍历整个搜索空间，在寻优精度也存在着一定的误差，为了克服这种误差，本文引入佳点集方法进行改进，以此使初始种群均匀散布在搜索空间里，通过上述改进，提出改进蝙蝠算法(Modified Bat Algorithm，MBA)。

本文在撒点区间[-10,10]内选取20个个体，通过佳点集方法进行撒点，如图1所示，20个个体均匀分布在撒点区间内，通过佳点集方法对初始化种群撒点切实可行，故本文将将佳点集方法用于蝙蝠算法，在算法搜寻初期初始化种群时，蝙蝠个体均匀分布在寻优区间内，大大提高蝙蝠算法的寻优效果。

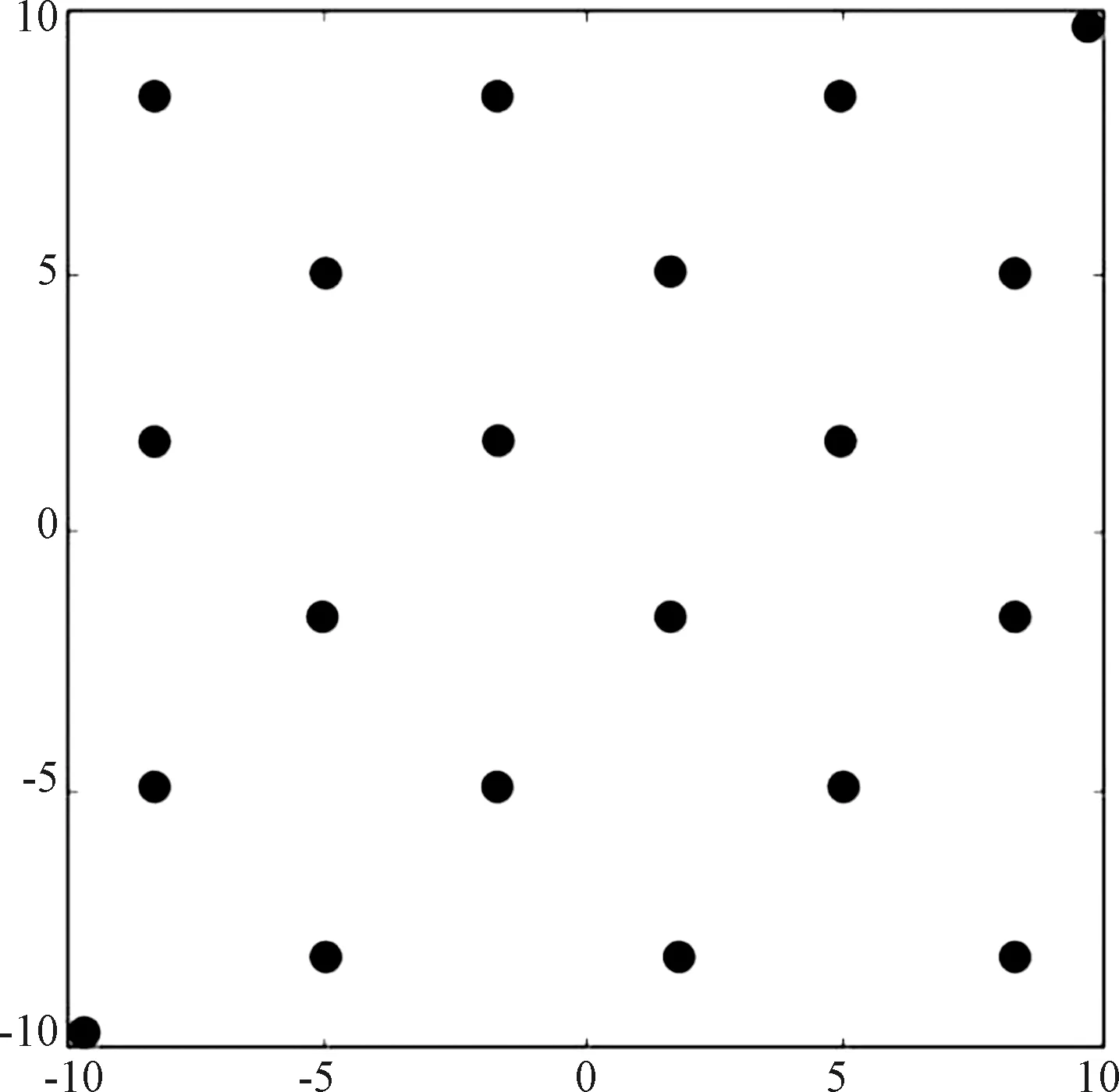
图1 佳点集方法产生的20个个体分布

3 算例分析

基于上述风电-抽水蓄能电站联合运行模型和蝙蝠算法，本文采用4台可逆式机组的抽水蓄能电站，抽水蓄能电站机组发电功率上限为300 MW，下限为170 MW，发电效率为0.94，额定抽水功率为330 MW，抽水效率为0.8，抽水蓄能电站上水库初始储能为6000 MWh，储能上限为10 000 MWh，下限为4000 MWh，考虑到上水库日常需水量，调度周期库容储能变化量上限为500 MWh，电网接纳功率上限为3200 MW，下限为800 MW，风功率预测数据为装机容量为4000 MW[10]，如图2所示。

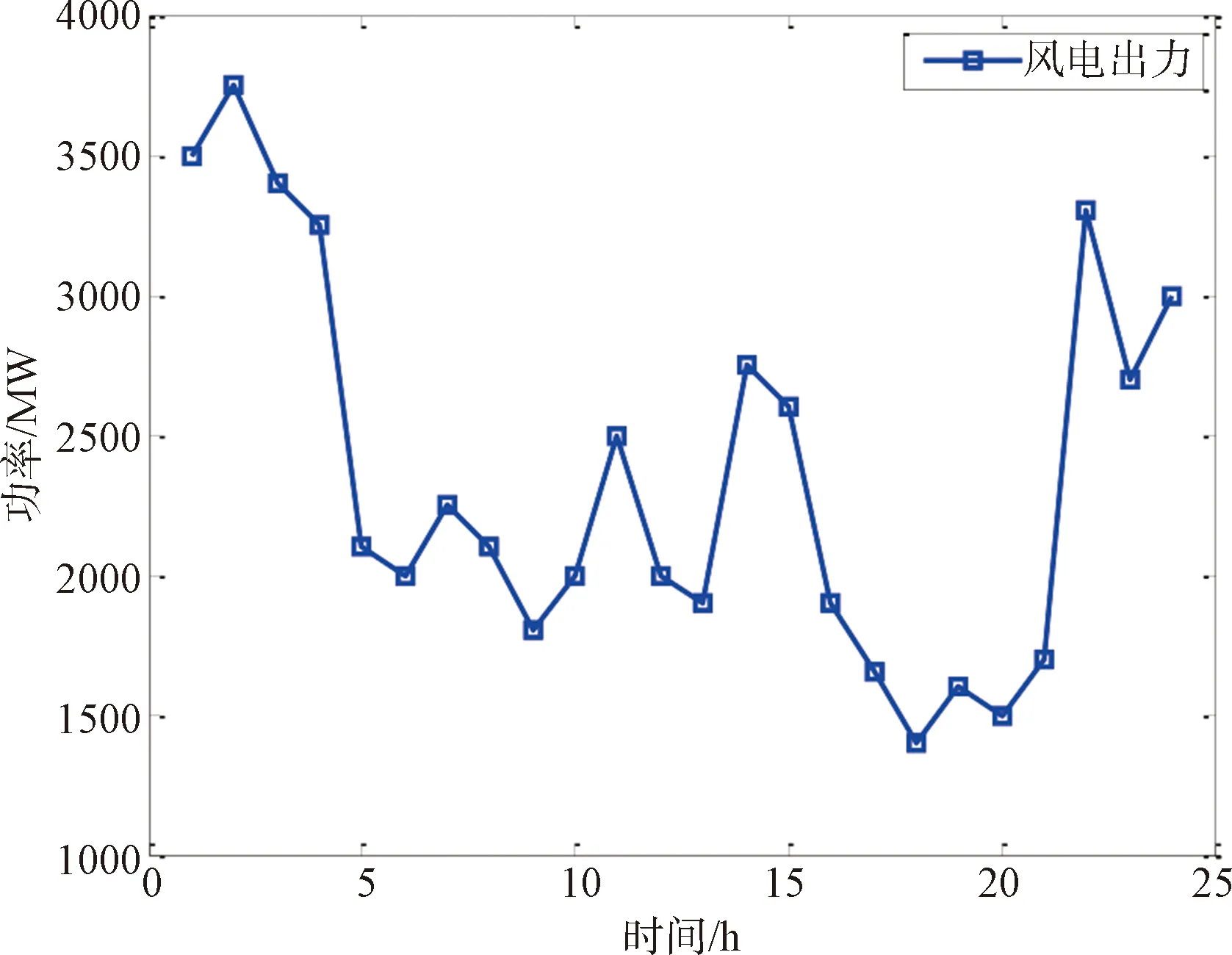
图2 风功率预测曲线样本

根据以上模型参数设置和处理方法，本文分别采用MBA、BA、PSO 3种算法进行优化对比分析，为保证对比效果的公平性，对于以上3种算法最大迭代次数设为500，种群规模均设为n=40，其中PSO的粒子学习因子C1=C2=1.4，惯性权重参数ωmax=0.9，ωmim=0.4，MBA和BA的脉冲最大发射率R=0.75，蝙蝠脉冲频率范围为[0，2]，发射率增加系数γ=0.05，最大响度A=0.25，减弱系数α=0.95。

图3为3种算法的仿真结果，适应度值即本文所求的标准差，MBA、BA、PSO的标准差分别为18.43 MW、22.60 MW、26.81 MW。对比3种算法的寻优曲线，可以发现PSO的适应度值最大，偏离目标值比较大，且寻优时间较长，远大于 MBA和BA；BA寻优结果和时间均适中；MBA寻优结果标准差最小，而且寻优时间最短，综上，MBA较常规智能算法PSO和原始算法BA在寻优时间和寻优精度均有大幅提高，有效避免了智能算法早熟、寻优精度差、寻优时间长等劣势，对于风蓄联合优化问题是一种理想的求解算法。

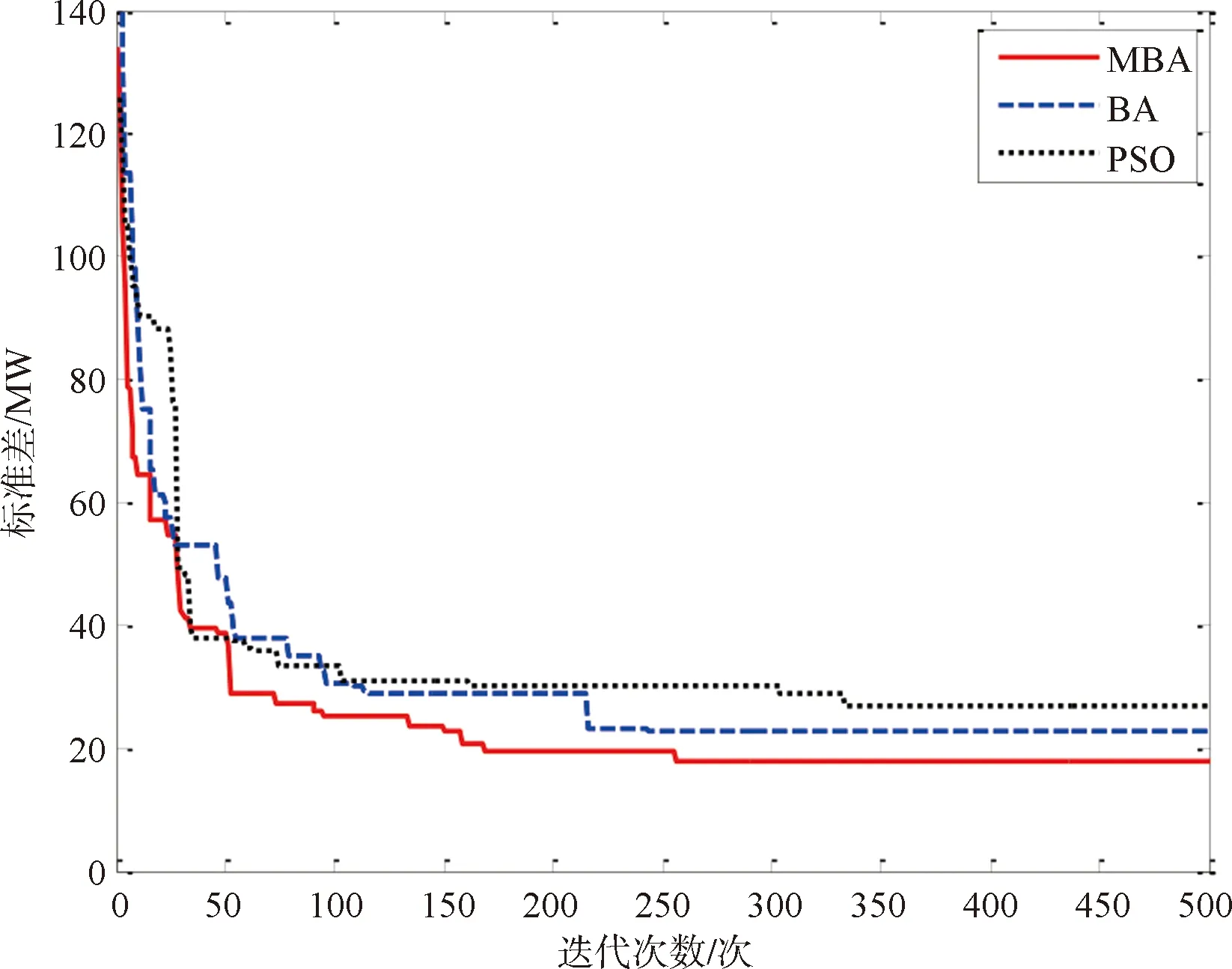
图3 3种算法寻优曲线

如图4所示，由风电出力曲线可知：风电输出功率标准差139.41 MW，第2时段为输出功率最高峰3750 MW，第18时段为输出功率最低谷1400 MW，峰谷差为2350 MW。由风蓄联合出力曲线分析可知，风蓄联合输出功率在第2时段为最高峰2430 MW，在第13时段为出力低谷2169.1 MW，风蓄联合出力峰谷差260.9 MW，对比可知：风蓄联合出力曲线峰谷差明显减小，风蓄联合运行的波动性大大减小，有效减小了风电出力的波动性。

图4 风电、抽蓄机组、风蓄联合出力曲线

如图5所示，为了评估大规模风电并网后，对电力系统其他机组出力的影响，此处将风电出力看作负的负荷，与原负荷叠加为等效净负荷，由负荷曲线可知：在第21时段为最高峰15 600 MW，在第3时段为最低谷7680 MW；由负荷-风电出力曲线可知：由于风电的并入，原负荷曲线的波动增大，峰谷差加剧；由负荷-风蓄联合出力曲线可知：风蓄联合系统的并入，峰谷差和波动性均小于负荷-风电出力曲线，大大减小了风电并入对系统的冲击。综上所述：风电具有典型的反调峰性，大规模风电并网，将对电网的稳定运行产生巨大的影响，当风电联合抽蓄电站运行后，可有效缓解风电的反调峰性。

图5 等效净负荷曲线

图6为抽水蓄能机组出力工况，其中出力为正表示机组处于发电状态；出力为负表示机组处于抽水状态。由出力曲线可知：在1-4、11、14-15、22-24时段，风电出力较大，抽蓄机组处于抽水工况；在5-10、12-13、16-21时段，风电出力较小，机组处于发电工况。综上，抽蓄机组在风电出力较小时发电，在风电出力较大时抽水，有效起到削峰填谷的作用。

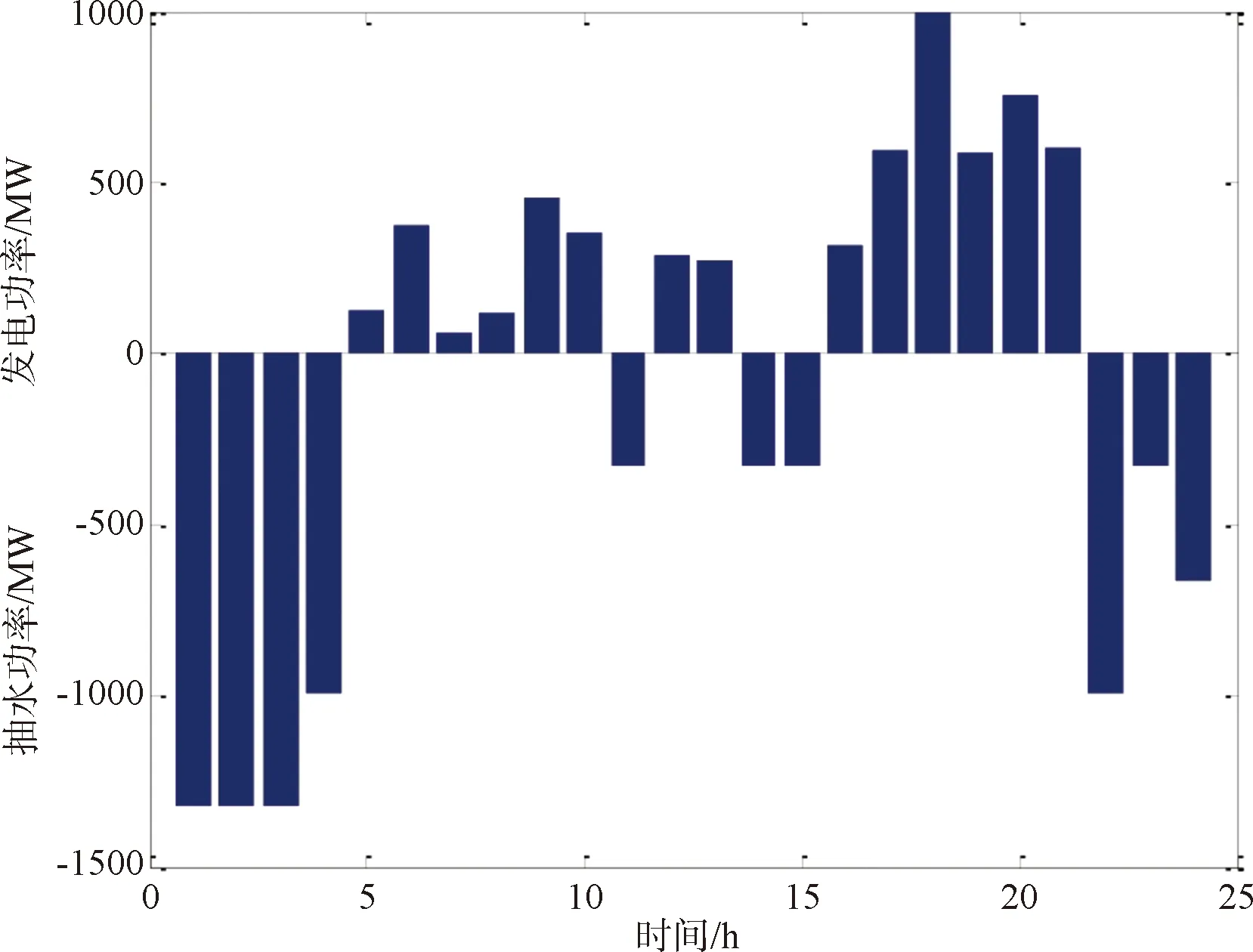
图6 抽蓄机组出力工况

图7为抽水蓄能电站上水库库容变化曲线，在第1-4、11、14-15、22-24时段，风电出力较大，抽蓄机组处于抽水工况，上水库库容不断增加；在5-10、12-13、16-21时段，由于风电出力较小，抽蓄机组处于发电工况，上水库库容不断减小。

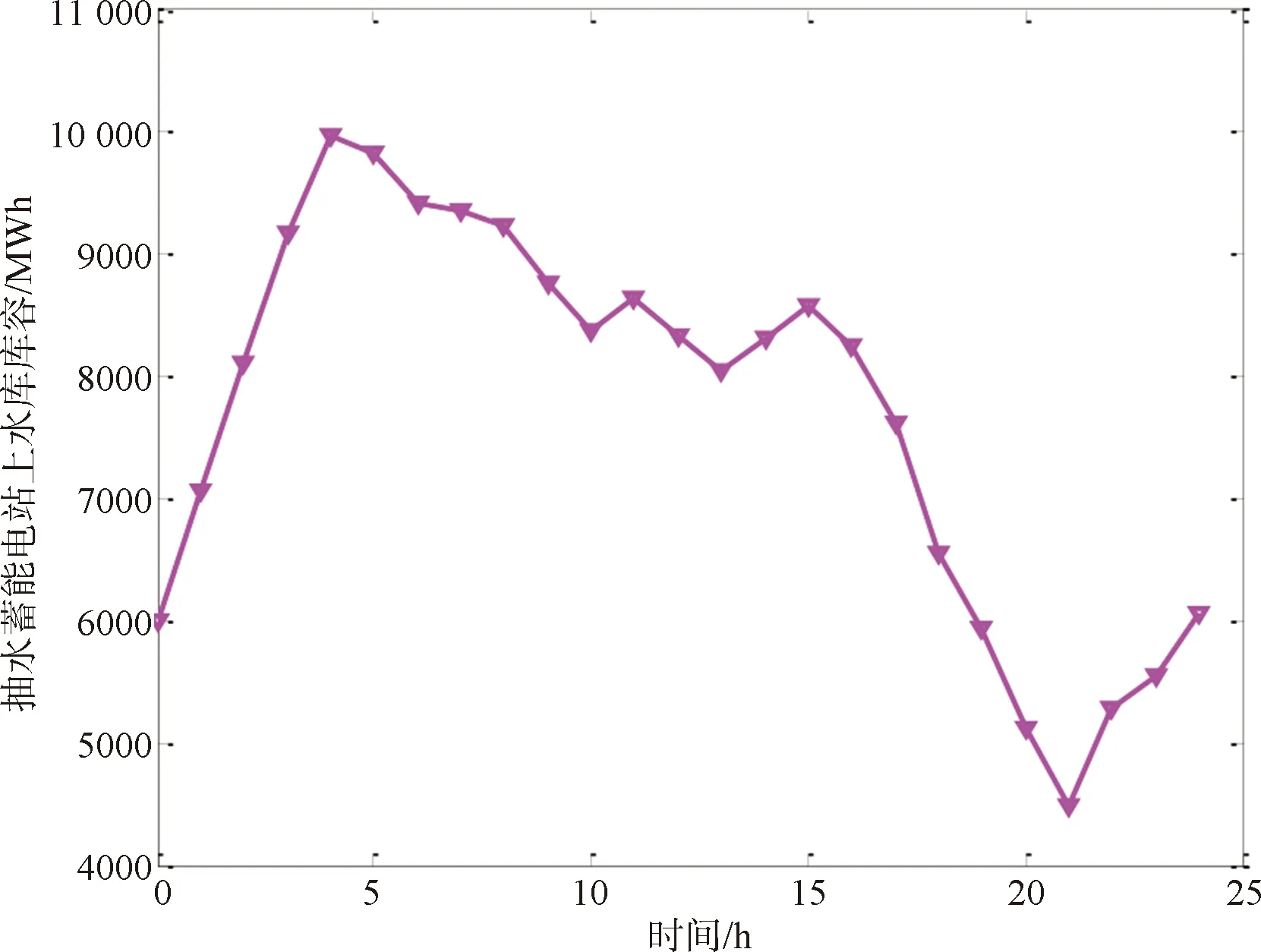
图7 上水库库容的变化曲线

由表1可知，风电单独运行输出功率的峰谷差为2350 MW，风蓄联合优化运行输出功率的峰谷差为260.9 MW，远小于风电单独运行的峰谷差，仅为风电单独运行时的11.1%，风电单独运行输出功率标准差139.41 MW，风蓄联合优化运行后输出功率标准差为18.43 MW，仅为风电单独运行时的13.22%，综上所述，本文风蓄联合运行模型在峰谷差、标准差方面效果显著，可以有效解决风电并网的局限性。

表1 模型优化结果

4 结论

本文首先建立了风电单独运行输出波动标准差模型，然后以风电-抽蓄联合系统输出波动标准差最小为目标，建立了风蓄联合系统优化运行模型，对模型的目标函数进行了分析，对等式和不等式约束进行了处理，分别采用粒子群算法、蝙蝠算法、改进蝙蝠算法进行模型求解，并对仿真结果进行对比分析，得到以下结论：①对于大规模风电并网问题，引入抽蓄电站，建立风电-抽水蓄能联合优化运行模型，可有效缓解风电对电网带来的冲击，切实减小风电输出功率的峰谷差和标准差；②对于风蓄联合优化问题，通过改进蝙蝠算法求解，在寻优精度、收敛速度等方面效果显著，改进蝙蝠算法可以有效解决风蓄联合系统优化问题。