Julia集“爆炸”的一族二次有理函数的参数空间
2021-04-07孙霞
孙 霞
(云南开放大学 公共教学部,云南 昆明 650500)
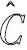
早在1918年,Lattès就找到了一个Julia集为整个Riemann球面的有理函数,即
利用Weierstrass椭圆函数的性质对此进行了证明,但deg(P)=4.在本文中,笔者找到了一族度为2的有理函数,其Julia集也是整个Riemann球面,由于该函数族中的函数与Lattès发现的函数不共轭,所以它们是新的Julia集为整个Riemann球面的有理函数,此外,熟知的有理函数
的Julia集也是整个Riemann球面,但它和我们函数族中的一个函数是共轭的,所以在函数族中.
若2个有理函数是共形共轭的,则它们就具有相同的动力学性质,从而在二次多项式的研究中,只需要研究如下的多项式即可:
Pc(z)=z2+c.
上述含有单参数的多项式族是一个动力学性质比较丰富的函数族,但由于∞是其超吸性不动点,所以它的Fatou集不会是空集,即Julia集不会是整个Riemann球面,也即不会出现Julia集“爆炸”的情况.而对同样的含有单参数的二次有理函数族
找到了使得其Julia集“爆炸”的具体参数值,并发现这些参数值构成的集合是一个无穷集,结论如下:
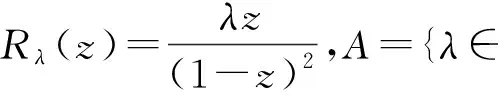
1 预备知识和引理
1.1 不动点及其分类

1)称z为R的超吸引不动点,如果λ=0;
2)称z为R的吸引不动点,如果|λ|<1;
3)称z为R的排斥不动点,如果|λ|>1;
4)称z为R的中性不动点,如果|λ|=1,进一步,若λ=e2πiθ且θ为有理数,则称z为有理中性不动点;若θ为无理数,则称z为无理中性不动点.无理中性不动点可以在Fatou集F(R)中,也可以在Julia集J(R)中.若无理中性不动点z∈F(R),则称z为Siegel点;若z∈J(R),则称z为Cremer点.
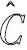
引理2[8-10]有理函数R的吸引和超吸引周期点属于F(R),排斥周期点属于J(R).
1.2临界点
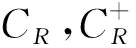
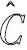
1.3 Sullivan定理
在介绍Sullivan定理之前,先介绍如下定义:
设R为次数不小于2的有理函数,D是Fatou集F(R)的一个分支,则称D是
1)周期的,如果存在某个正整数n,使得Rn(D)=D;
2)预周期的,如果存在某个正整数m,使得Rm(D)是周期的;
3)游荡的,如果集合{Rn(D),n≥0}是两两互不相交的.
早在上个世纪初,Fatou就猜想,对有理函数来说,不存在游荡的Fatou分支,这个猜想直到Sullivan引进了有理函数的拟共形形变才获得证明,结论如下:
引理4[8-10](Sullivan定理) Fatou集的每一个分支都是预周期的.
1.4 Sullivan分类定理
引理5[8-10]设R是有理函数,deg(R)≥2,如果D是R的不变Fatou分支(即R(D)=D),那么,D为下列5种情形之一.
1)吸引的:存在R的吸引不动点z0∈D,其乘子λ满足0<|λ|<1,Rn在D内局部一致收敛于z0;
2)抛物的:存在R的有理中性不动点z0∈∂D,乘子λ=e2πiθ且θ为有理数,Rn在D内局部一致收敛于z0;
3)超吸引的:存在R的超吸引不动点z0∈D,乘子λ=0,Rn在D内局部一致收敛于z0;
4)Siegel盘:D共形等价于单位圆盘Δ,而R共形共轭于Δ上的无理旋转z|→e2πiθ,z∈Δ,θ为无理数;
5)Hermann环:D共形等价于环域A(r,1)={z|0 引理6[8-10]设R为度deg(R)≥2的有理函数,则R的每个吸引(超吸引)循环的直接吸性域中至少含有R的一个临界点. 引理7[8-10]设R为deg(R)≥2的有理函数,则R的每个抛物循环的直接吸性域中至少含有R的一个临界点. …… λ+4=0. (1) 4λ2+(λ+4)2=0. (2) 4λ3(λ+4)2+((λ+4)2+4λ2)2=0. (3) 从上述证明中不难发现,Α⊂{λ||λ|≥1}.因为0为Rλ的其中一个不动点,若0<|λ|<1,则0是Rλ的吸引不动点,由Sullivan分类定理,存在包含原点的Fatou分支D,此时Julia集不会是整个Riemann球面;若|λ|=1且λ为有理数,则0为有理中性不动点,此时也存在Fatou分支D,使得0∈∂D,Julia集也不会是整个Riemann球面;若|λ|=1且λ为无理数,则0可以是Siegel点也可以是Cremer点,此时只有0是Cremer点时Julia集才会是整个Riemann球面.但对集合A的具体状况不得而知,猜测A可能有内点或者有有限的聚点.1.5 稳定域与临界点之间的关系
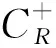
1.6 Julia集为整个Riemann球面的充分条件
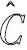
1.7 代数学基本定理
2 定理的证明