山地景区观光电梯故障情况下人员疏散分析

张 雨，卢 婷

(1.昆明理工大学 建筑工程学院，云南 昆明 650500； 2.云南省消防救援总队技术处，云南 昆明 650200)

观光电梯在山地丘陵地区的旅游开发中有广泛的应用，目前在湖南张家界百龙、四川雅安碧峰峡、湖北施恩大峡谷和河南林州等地都建成了山地景区观光电梯。与一般民用高层建筑紧急情况下人员只可以向下单向疏散不同的是，此类建筑由水平长廊和垂直交通建筑联系山脚和山顶，电梯故障情况下人员可在电梯停靠层经过楼梯同时向山顶和山脚安全出口疏散。目前对于紧急情况下人员经楼梯、电梯、楼-电梯疏散的研究也较多。王芳等[1]提出了在高层建筑疏散中依靠楼梯疏散的潜在高风险楼层优先疏散的策略；王超[2]通过定量分析电梯、楼梯的疏散表现，验证了高层电梯辅助疏散的高效性，提出了电梯提升效率的衡量指标；陈海涛等[3]、杨海明[4]、郭晓明等[5]运用数学模型就高层建筑楼-电梯耦合疏散进行了研究，指出存在使楼-电梯耦合疏散效率最高的最佳分离楼层。陈海涛[6-7]针对人员疏散的出口选择行为进行了研究，提出了相应的人员疏散模型，并进一步研究了影响出口选择的距离、密度和出口宽度等因素；袁慧[8]分别采用经验公式和Pathfinder仿真模拟计算分析了高层建筑疏散时间；丁元春[9]根据建筑物特征、人员属性等，通过运用Pathfinder仿真模拟研究了疏散人群在楼梯的汇流情况等疏散特征。但是类似景区观光天梯类建筑的人员疏散研究较少。根据相关规范[10]，建筑的疏散楼梯宜直通屋面，可使人员多一条疏散路径，有利于人员避难和逃生。因此，可将观光建筑山顶方向疏散出口视为建筑屋面避难层。针对该情况，本文在已有单向疏散计算方法的基础上，推导了电梯故障时被困人员双向疏散过程的简化计算方法，结合实际案例，采用简化计算方法和人员疏散仿真软件Pathfinder数值模拟进行了对比研究，验证了天梯建筑简化疏散计算方法的有效性，在此基础上进一步分析了适用于该类建筑的疏散策略，以提高紧急疏散效率。

1 楼梯疏散计算模型

天梯建筑楼梯疏散时间的计算模型借鉴了MELINEK和BOOTH及PAULS等研究的经验公式[11-12]，该模型中人员运动时间由人群经过出口时的排队时间和人员在楼梯上的穿行时间组成，即：

T=TD+TC。

(1)

式(1)右边第一项为通过各个出口时的排队等待时间总和，第二项为楼梯中的穿行时间，分别按如下公式计算，

(2)

TC=rts。

(3)

式中，k为经过出口的数量；Ni为通过出口i的人数，人；Wi为出口i的宽度，m；Ci为出口i的通行速率，人·(m·s)-1；r为穿行的楼层数；ts为通过一层楼的楼梯所需要的时间，s，常取16 s[13]，当建筑层高较大时；ts取值可适当增大。

在考虑双向疏散的情况下，假设ρ为向上疏散的人数比例，n为总的楼层数，按照式(1)—(3)可推导得上行运动时间TU、下行运动时间TL分别为：

(4)

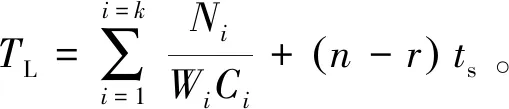
(5)

依据式(4)，式(5)可知，当人数、出口给定的情况下，TU，TL是停靠楼层r的线性函数，其基本示意见图1所示。

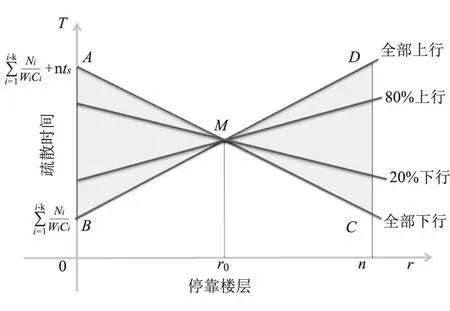
图1 停靠层疏散人数比例及方式与疏散时间关系Fig.1 Relationship between the people on each floor and evacuation time

图1给出了ρ=1时(全部上行疏散)和ρ=0时(全部下行疏散)的疏散时间随停靠楼层的变化关系，两个三角阴影区域(ΔABM，ΔDMC)分别绘出了在不同ρ值情况下人员运动时间的上界和下界，交点M处的坐标按如下方程计算：

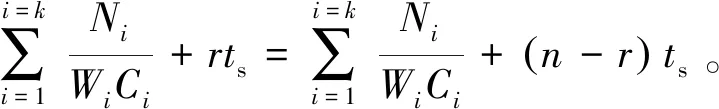
(6)

计算得到ro=n/2。当ρ≠0或ρ≠1时，为双向疏散，TU，TL曲线为上述三角形范围内过M点的两条直线，疏散运动时间取TU，TL的大值，显然在这种情况下，不会出现最优的疏散时间；当ρ=0或ρ=1时，为单向疏散，最小疏散运动时间取为曲线BMC上的值，即当r≤n/2时，取TU时可获得运动时间的下限，当r≥n/2时，取TL可获得运动时间下限。因此，结合图1，不难看出对于此类疏散，有如下特征：

(1)在ρ≠0或ρ≠1时，即双向疏散时不可能获得疏散运动时间的下限值，只能获得疏散时间上下限之间的一个值，不能获得最优的疏散运动时间；

(2)在ρ=0或ρ=1，即单向疏散时，若停靠楼层小于ro，则选择向上疏散时，可获得最小运动时间，当停靠楼层大于ro，选择向下疏散可获得最小疏散运动时间。

2 案例分析

2.1 工程概况

某景区观光梯建筑，由山顶部分横向120 m长双层观光长廊及配套建筑和山脚至山顶160 m(层高5.4 m)高的垂直交通联系建筑(山脚直通山顶观景平台的观光电梯)两部分组成，见图2所示。

图2 天梯pathfinder模型示意图Fig.2 Schematic diagram of the ladder pathfinder model

山脚天梯建筑为垂直交通联系建筑，可在0 m处通过观光电梯直达-135 m山脚下，旅客可从山脚和山顶安全出口疏散至室外，垂直天梯设有三部观光电梯，电梯门宽0.8 m，单个电梯荷载人数取18人，且电梯厅设有一部检修楼梯，电梯到楼梯间距离约9 m，楼梯前室两门均宽1.2 m，楼梯间宽3.0 m，单跑楼梯段宽度1.3 m，单跑梯段长约4 m，检修楼梯间详图如图3所示，其可供检修人员使用，也可作为观光旅客疏散使用。

图3 天梯检修层平台平面图Fig.3 Plan of the ladder repair platform

2.2 楼梯疏散时间数值模型

结合上述天梯建筑，为验证疏散运动时间计算公式的可靠性，运用疏散仿真软件Pathfinder进行对比计算分析[14]。疏散过程中的人员组成、平面行走速度参考Simulex软件的建议值进行分析，人员在楼梯间疏散速度，参考了美国消防工程师学会(society of fire protection engineers，SFPE)手册[15]，见表1所示。电梯门、楼梯间门、楼梯入口处的通行速率也参考了SFPE手册，均取为0.8人·(m·s)-1。而对于楼梯段上运行时间ts取值，由于该天梯建筑层高较高，按表1参数计算得到20 s[16]。

本文为分析不同停靠楼层的疏散策略，分别用Pathfinder 模拟和式(4)、式(5)手算计算了停靠楼层为-4层、-8层、-10层、-12层、-16层时的疏散时间，数值模型见图4、5所示，疏散模拟过程中ρ分别取为0，1，0.5 三种情况。

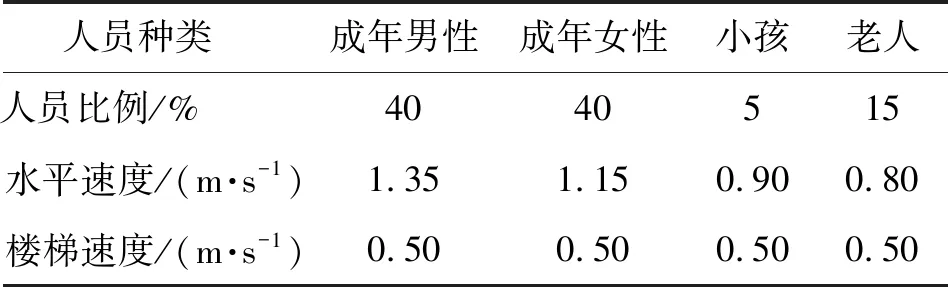
表1 人员参数表Tab.1 Personnel parameter table

2.3 计算结果对比分析

根据计算、数值模拟结果，各场景下的计算结果对比如下图4、5所示，图4(a)给出了向上、向下单向疏散的结果，图4(b)中给出了在50%向上疏散和50%向下疏散的结果；图5(a)给出了最优的单向疏散运动时间，图5(b)给出了最优疏散运动时间与单向疏散运动时间的关系，显然可知：(1)单向疏散或双向疏散都具有上图1所示的三角形区域的特征；(2)比较图4(a)和图4(b)不难发现，所有对应楼层位置双向疏散运动的时间均在单向疏散两条包线划定的时间范围之内，这与图1所示的结果也是一致的；(3)由图5(b)可以看出，在双向疏散场景下，疏散时间为整个疏散时间的大值，所以，最优的疏散时间出现在单向疏散的情况，双向疏散时不可能获得疏散运动时间的下限值。

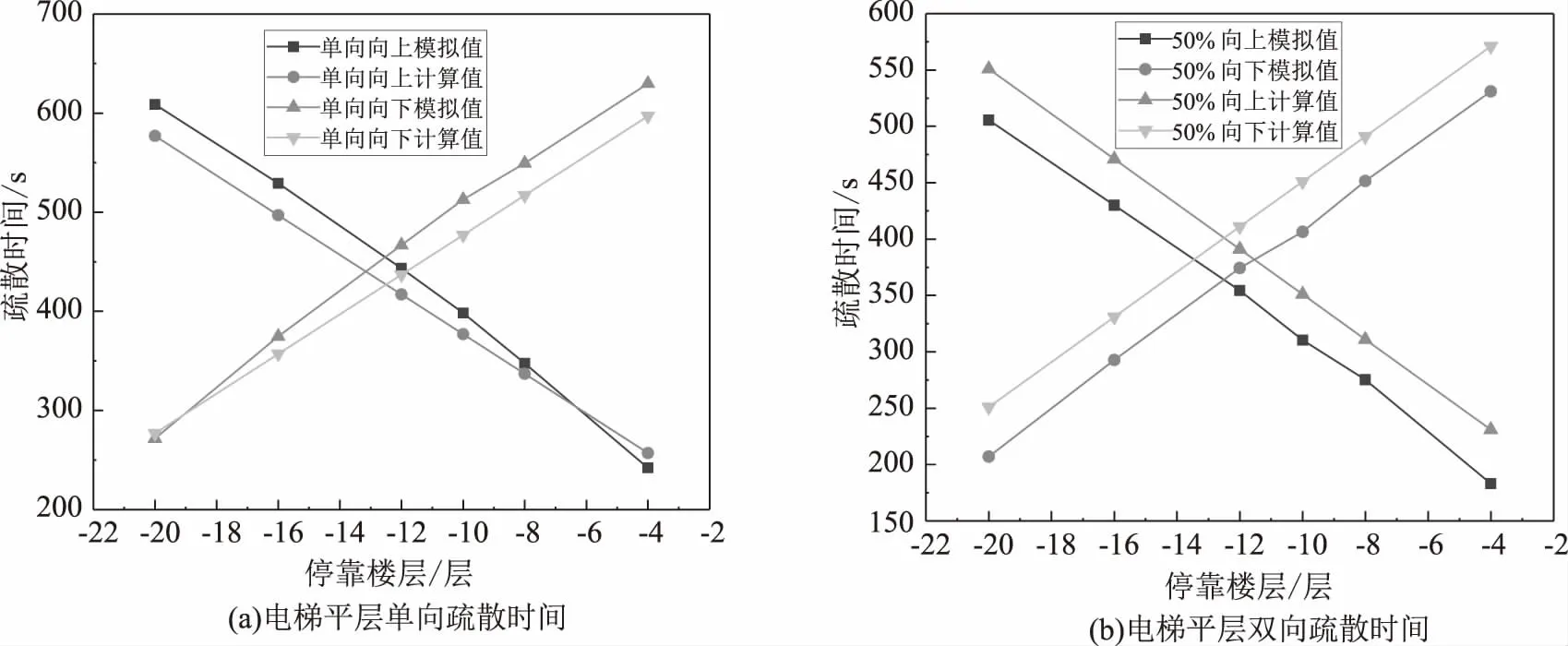
图4 电梯平层单双向疏散时间图Fig.4 Single and two-way evacuation time diagram of elevator leveling

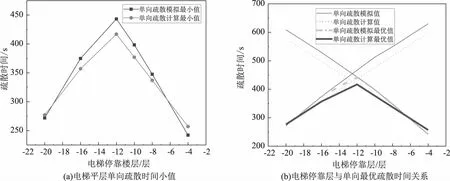
图5 疏散时间对比图Fig.5 Comparison of evacuation time

另外，根据以上图4、5可知，对于该景区观光天梯建筑，在最优疏散效率下，最佳分离楼层为建筑高度中间楼层，可将建筑高度中点作为电梯紧急停靠时人员单向向上或向下疏散的疏散行为分界点。且由图5(a)可知，在单向疏散条件下，建筑中间层位置疏散最优时间出现折点，说明建筑最佳分离楼层上下相同距离处疏散时间基本一致，即建筑中点上下相同位置处的疏散时间具有对称性。

以上各疏散时间对比图可知，各楼层人员疏散时间简化公式计算结果与Pathfinder仿真模拟所得结果较为吻合，简化计算公式在运用于天梯类建筑人员疏散分析时具有一定可靠性。

3 结论

为研究天梯观光建筑电梯故障情况下的疏散特点及优化疏散策略，分析了此类建筑的疏散特点，推导了人员运动时间的计算公式，在此基础上，以一实际工程为研究对象，结合Pathfinder模拟进行了对比验证，结果表明：

(1)对于观光天梯类建筑，对比分析表明，简化计算方法可以较为准确地估计人员的疏散运动时间；结合疏散运动时间的三角形范围，可以估计在一般双向疏散情况下疏散时间的上下界。

(2)天梯建筑人员最小运动时间仅能在单向疏散的情况下获得，双向疏散情况下的总时间，总比按最优单向疏散方式的时间大。

(3)在电梯停靠层在总建筑高度的一半以上时，单向向上疏散可获得最小的疏散运动时间，在电梯停靠层在总建筑高度的一半以下时，单向向下疏散可获得最小的疏散运动时间。