基于L-BFGS-B局部极小化的自适应尺度CLEAN算法

张 利，肖一凡，米立功，卢 梅，赵庆超，王 蓓，刘 祥，张 明，谢 泉

(1.贵州大学 大数据与信息工程学院，贵州 贵阳 550025；2.中国科学院新疆天文台，新疆 乌鲁木齐 830011)

通过观测所接收到的电磁辐射来认识宇宙结构，理解宇宙起源及演化，是人类不断追求的目标。在射电波段对天体和宇宙开展研究的天文学分支称为射电天文学。近年来，射电天文学取得了显著突破，包括脉冲星和中子星[1]、星系中的暗物质[2]、由超大质量黑洞驱动的射电星系[3]和类星体[4]等，这对于理解宇宙、恢复宇宙图景具有重要意义。

研究宇宙演化的重要手段之一是研究射电天文图像及其结构变化。由于银河系外天体(例如类星体和星系)的射电辐射到达地球时信号已经非常微弱，只有借助具有较高灵敏度的大型射电干涉阵列才能检测到这些信号。目前已建成的大型干涉阵列包括巨米波射电望远镜(giant metrewave radio telescope， GMRT)、默奇森宽场阵列望远镜(murchison widefield array，MWA)、低频阵列射电望远镜(low frequency array，LOFAR)，此外还有若干正在建设的新型干涉阵列，例如平方公里射电阵(square kilometre array，SKA)。

随着越来越多的巡天计划的实施和大型干涉阵列的建成，人们能够得到海量天文数据，但是望远镜数量有限和地球自转综合造成的稀疏采样使射电天文图像变得模糊。为了对源的结构特性做更精准的分析，需要对观测到的射电天文图像进行去模糊处理。Högbom[5]开创性地提出了CLEAN反卷积算法，通过迭代识别点源并消除点扩展函数(PSF)的影响，有效解决由于稀疏采样引起的图像模糊问题。该算法的提出具有超越时代的意义，并延伸应用到其它领域。CLARK算法[6]和Cotton-Schwab算法[7]对其作出改进，在提高反卷积速度的同时，减少算法误差，对展源的处理更加精准。然而点源分解机制和点扩展函数的旁瓣导致包含延展源和复杂特征的重建图像中出现条纹(stripes)。研究人员提出了一些改进算法解决该问题，例如，尺度敏感的CLEAN算法[8-12]，利用尺度基函数将天文图像参数化，以表达像素之间的相关性，从而进一步消除图像残差，但对于重建图像质量仍有提升空间。本文提出一种自适应尺度CLEAN算法，通过局部极小化目标函数，寻找最优分量，以提高反卷积的性能，从而更加精准地重建射电天文图像。

1 理论基础

1.1 干涉成像原理

天空亮度分布可以分解为奇对称成分和偶对称成分，在射电天文望远镜进行动态范围成像时，使用一对cosine 和 sine 相关器的组合，即复相关器，来输出天空图像的可见度：

(1)

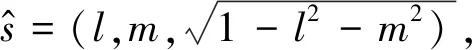
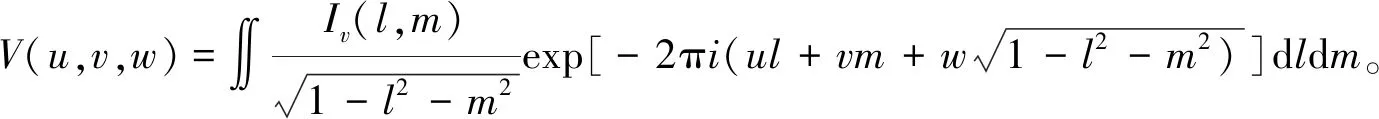
(2)

在满足小视场成像和所有基线矢量共面的情况下，上式可消去w额外项，变为二维傅里叶变换，然后通过逆傅里叶变换，得到天空亮度分布。

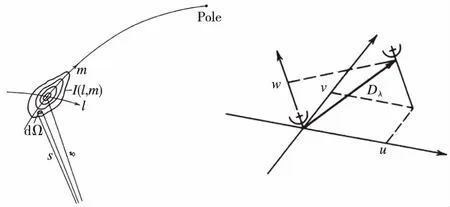
图1 干涉仪成像中常用的(u,v,w)直角坐标系[13]Fig.1 The (u,v,w) rectangular coordinate system commonly used in interferometer imaging

受限于干涉阵列的天线数目和基线的长度范围，所观测的uv平面覆盖不完全，因此无法获得天空亮度分布的全部信息，傅里叶逆变换仅能得到脏图Idirty(l,m)，

(3)

其中，S(u,v)表示采样函数。采样函数是干涉阵列的点扩展函数B(l,m)的傅里叶变换。根据卷积定理，上式可表示为：

Idirty(l,m)=I(l,m)*B(l,m)。

(4)

脏图存在明显的旁瓣等干扰，无法反映真实的天空亮度分布，因此利用反卷积算法，例如CLEAN算法、最大熵算法[14]，从脏图中尽可能地对真实射电天文图像进行重建。

1.2 Högbom CLEAN算法

Högbom提出的CLEAN算法将天空亮度分布假设为一系列点源集合，在图像域中通过迭代洁化的过程，消除脏图中的旁瓣效应。对Högbom CLEAN(Hg-CLEAN)算法的具体实现过程如下：

步骤1寻找脏图中最大绝对亮源，取其位置(xi,yi)和幅度ai作为初始参数；

(5)

其中，g表示循环增益；

步骤3更新第i次残差图像，Iiresidual=Idirty-B(l,m)*Iimodel。

(6)

其中，*表示卷积运算；

步骤4重复步骤1—3，直到迭代次数超过预设阈值或残差图像中的最大值小于规定的噪声水平时停止。将洁束卷积模型图像，再加上残差图像，得到恢复出来的图像。

这种算法对于点源集合的处理具有很好的效果，然而点源无法表示延展源中像素间的相关性，因此不能很好地重建展源。

2 基于L-BFGS-B局部极小化的自适应尺度CLEAN算法

受CLEAN算法[5,12]和文献[15]的启发，本文提出一种L-BFGS-B局部极小化的自适应尺度CLEAN算法，和其它CLEAN算法的变种一样，使用相同的框架[10]。本文引入的L-BFGS-B算法由L-BFGS算法[16]改进得到，是一种基于梯度投影的非线性优化方法。该方法结合原有算法的Hessian、线搜索算法和信任域方法应用于更新过程。

图2 本文算法框架Fig.2 The framework for our algorithm

L-BFGS-B算法的迭代公式为：

xi+1=xi-αiHi▽fi。

(7)

其中，αi表示步长调节因子，Hi为Hessian矩阵，▽fi为多维一阶向量梯度。Hi通过公式在每次迭代中更新参量，

(8)

Vi=I-ρiyisiT；

(9)

si=xi+1-xi；

(10)

yi=▽fk+1-▽fk。

(11)

在本文算法的每一次迭代中，L-BFGS-B算法按照以下步骤寻找最优解：

步骤1结合信任域方法，根据下列公式在点xi附近用二次型模型对目标函数进行局部拟合，计算柯西点的近似值，

(12)

其中，()T表示转置运算，Hi表示在第i次迭代的Hessian矩阵；

步骤2 通过直接法、共轭梯度法或对偶法计算搜索方向dk；

步骤3依据问题的约束条件，沿搜索方向dk进行线性搜寻，计算步长调节因子αk，更新参数xk+1=xk+αkdk，以寻找函数的最小值；

步骤4采用L-BFGS-B算法更新Hessian矩阵Hk，同时检查是否收敛。

重复步骤1—4，直到满足L-BFGS-B算法的3个停止准则之一：达到最大迭代次数、目标函数的减少量变小时，投影梯度的范数足够小时，循环终止。从而得到函数最小值，阈值的选择取决于脏图和点扩展函数的实际情况。

然后，利用一系列高斯函数对残差图像进行平滑处理，取结果的最大值作为初始参数，

(13)

其中，ωi表示第i次迭代中重新计算得到的高斯模型的尺寸，ωic表示第i次迭代中由最小化算法拟合残差得到的高斯模型尺寸，ωb是点扩展函数的高斯模型尺寸的近似值。优化后的幅值ai可由下式计算得到：

(14)

其中，aic和ab分别表示拟合残差得到的幅值和点扩展函数的模型幅值。接着，计算模型尺度的大小，并根据高斯尺度得到第i次拟合后的模型分量：

(15)

使用该最优分量对模型图像进行更新，同时利用循环增益g对模型分量进行优化，以建立更加精确的天空模型，

(16)

其中，Iimodel表示第i次迭代的模型图像。接着利用模型图像计算残差图像，更新第i次残差图像，

Iiresidual=Idirty-B(l,m)*Iimodel。

(17)

其中，*表示卷积运算。对模型和残差图像进行循环更新，直到满足最大迭代次数或者达到噪声水平时停止，得到最后的模型图像Imodel和残差图像Iresidual，重建后的图像Irestored表示如下公式：

Irestored=Bclean*Imodel+Iresidual。

(18)

其中，Bclean为拟合主瓣得到的干净光束。改进后的算法流程如图2所示。

本文采用L-BFGS-B算法对分量进行更准确的拟合。对比Hg-CLEAN算法，该算法通过对最小化目标函数部分的优化，能够对天空亮度分布做出更精准的建模，使重建后的图像更加接近真实天空图像。

3 试验结果分析与算法评估

本文使用天文通用软件包(common astronomy software applications,CASA)模拟JVLA B阵型观测仙女星系M31图像，并用于验证新算法的性能，图像尺寸为256×256像素。图3展示了本算法重建图像前后的对比效果。对比图3(a)中参考的干净天空图像，图3(b)显示了在点扩展函数旁瓣影响下的脏图，其中包含大量的旁瓣，造成图像中天体的细节结构模糊不清。图3(c)是本文算法实现的图像重建效果，从图中能够观察到，脏束的旁瓣效应基本被消除，天空图像中的点源和展源附近的模糊得到较好的处理，说明本文算法能够从脏图中有效重建天空图像。

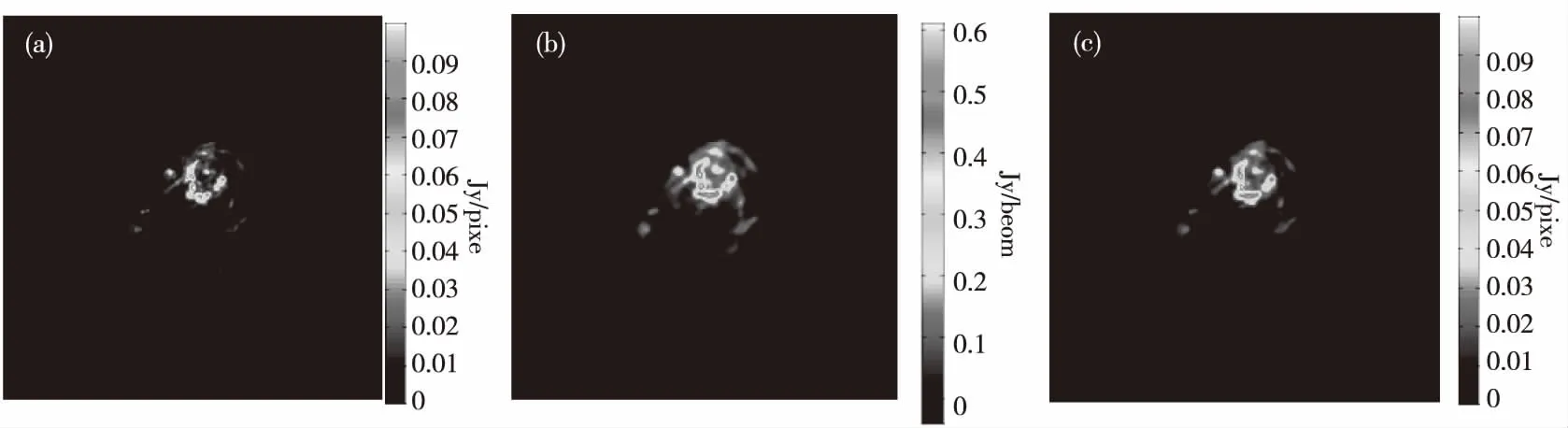
(a)原始图像；(b)脏图；(c)重建图像图3 本算法重建图像对比效果Fig.3 Contrast effect of the algorithm

相对于Hg-CLEAN算法，本文算法呈现出更好的图像重建性能。图4是本文算法与传统的Hg-CLEAN算法对于同一图像的处理结果，展示了对应的模型图像和残差图像。从图中可以看出，本文算法得到的残差图像中的结构远少于Hg-CLEAN算法，说明采用该算法得到的重建图像，能够恢复原始图像中的大部分信息，同时能够体现L-BFGS-B算法的拟合参数效果良好，提高了算法对天空亮度分布建模的精度；观测最终的重建结果，发现Hg-CLEAN算法也能够对原始图像的部分信息进行重建，然而在最终的结果中仍带有大量的伪影，并且在其残差图像中包含明显的图像结构。

(a1)Hg-CLEAN算法的模型图像;(a2)Hg-CLEAN算法的残差图像;(b1)本文算法的模型图像; (b2)本文算法的残差图像图4 不同算法的重建结果Fig.4 Reconstructed results from different algorithms

另外，从图4(a2)中能够观察到明显的延展信号，图5展示了模型图像中展源部分的处理效果。与Hg-CLEAN算法相比，本文提出的算法在展源处理方面效果更好，原因在于Hg-CLEAN算法将天空图像分解为一系列delta函数，不能很好地表达图像中的展源结构，而本文算法能够依据射电天文图像中的展源结构自适应地选取尺度参数，因此具有处理图像中延展源的性能。

(a)原始图像;(b)Hg-CLEAN算法的处理结果;(c)本文算法的处理结果图5 展源部分的局部特征图像Fig.5 The local feature image of the source part

同时，采用客观指标对天空图像重建效果做量化分析，选取峰值信噪比(peak signal-to-noise ratio,PSNR)[17]、结构相似性(structural similarity,SSIM)[18]和均方根误差(root mean square error,RMSE)[19]作为重建图像的质量评价指标，对Hg-CLEAN算法和本文提出的算法进行评价。为了对比不同算法之间的差异，在同样运行环境下对不同算法进行测试，从表1可以看出，本文提出算法在PSNR、SSIM和RMSE指标上均有所提升。

表1 重建图像质量指标比较Tab.1 Reconstructed image quality index comparison

为了验证算法的稳定性，采用三种加权方案对原始图像做处理，即自然加权, 均匀加权和Briggs 加权。图6展示了不同加权方案下图像的结构变化，观察可以发现经自然加权后的图像中的旁瓣效应最为明显，均匀加权后的图像的旁瓣效应最弱。

(a)自然加权;(b)均匀加权;(c)Briggs加权图6 不同加权方案下的脏图Fig.6 Dirty images of different weighting schemes

图7显示了对于不同加权方案的重建结果。对比残差图像，本算法对不同加权下的脏图均有较好的重建效果，尤其对于均匀加权和Briggs加权具有明显优势。

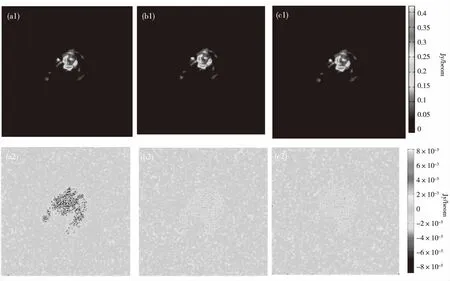
(a1)自然加权的重建图像;(a2)自然加权的残差图像;(b1)均匀加权的重建图像;(b2)均匀加权的残差图像; (c1)Briggs加权的重建图像;(c2)Briggs加权的残差图像图7 不同加权方案下的重建效果对比Fig.7 Comparison of reconstruction effects under different weighting schemes

4 结语

CLEAN算法对于射电天文图像处理领域具有重大意义，并能够延伸到天文学相关的其他领域[20]，这系列算法对传统的图像处理算法造成冲击，对图像处理的相关领域也产生了深远影响。本文基于目前已有的CLEAN算法[12]，结合L-BFGS-B算法对目标函数的最小值求解进行优化，并将算法的重建结果与传统的Hg-CLEAN算法[5]做比较，提高了原有算法的性能，使重建得到的射电天文图像更加接近真实天空图像，为测试该算法对不同观测图像的普适性，在以后的工作中，计划扩展到不同阵列和不同科学目标的观测成像中去。