气垫式调压室水位和气室压力波动及状态方程多方指数影响计算研究

杨 丹，鞠 小 明，2

(1.四川大学水利水电学院，四川 成都 610065；2.四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065)

0 引 言

气垫式调压室是一种由室内边壁和水面围成的封闭气室，不仅可以反射压力钢管传来的水锤压力波，而且利用气室内空气的可压缩性极大抑制了调压室水位波动的幅值。因此，气垫式调压室气室压力高于大气压力，调压室稳定水位会低于常规调压室，水位波动幅值也会小于常规调压室，其高度不需很高，调压室的位置选择更为自由，特别适用于地形险峻地区高水头、小流量的中小型水电站，具有对山坡植被环境破坏影响小、工期短、投资省等优点[1-3]。关于气垫式调压室的水位波动计算方法主要有两种：一是将气垫式调压室作为电站输水系统瞬变流计算中一个边界元件，运用瞬变流理论计算其水位变化，该方法需要专门计算软件和对引水系统管段进行分段，优点是不仅可以计算气垫式调压室水位波动过程，同时还能计算各管段断面的水锤压力[4-5]；二是将电站输水发电系统作为集中质量系统，直接使用引水隧洞动力方程和气垫式调压室连续方程进行求解，该方法优点是求解快速方便，不需要压力钢管和水轮机等方面的资料，缺点是仅能计算气垫式调压室水位波动过程，不能计算水锤压力。其中后一种方法看似简单，对常规调压室也常常这样做[6]，由于气垫式调压室中空气压缩和膨胀过程中的多方指数问题[7]，会使引水隧洞动力方程变成非线性，需要对引水隧洞的动力方程进行适当变化才能采用四阶龙格——库塔法进行快速求解，本文主要利用这种方法，分析气体状态方程多方指数对调压室涌浪水位和气室压力的影响。

2 气垫式调压室水位波动四阶龙格—库塔快速计算法

带气垫式调压室水电站有压引水系统的示意图如图1所示。

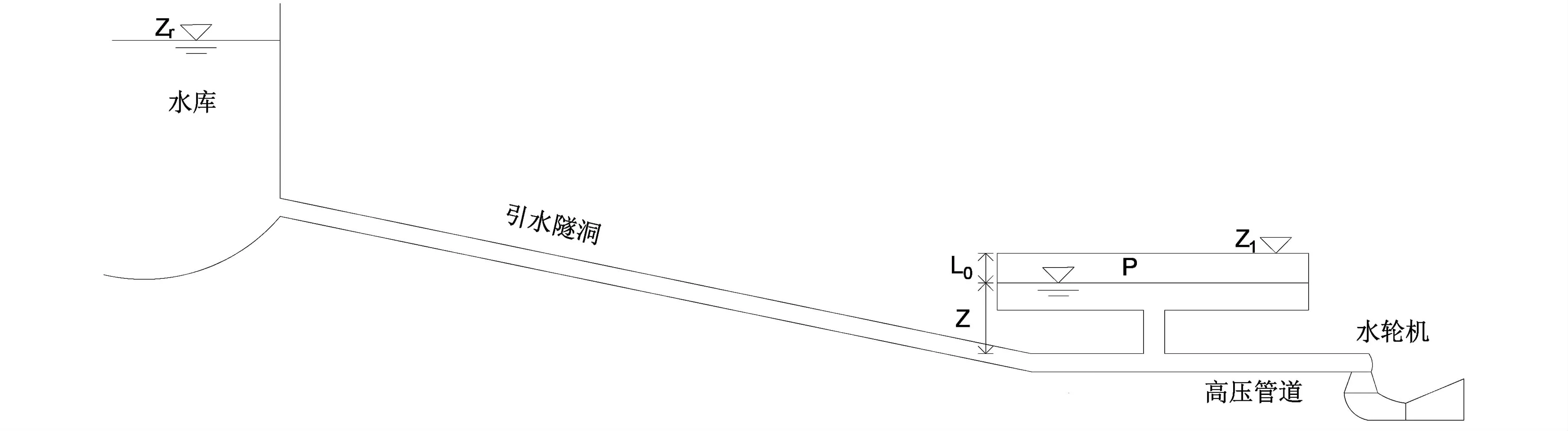
图1 带气垫式调压室水电站有压引水系统示意图

基本假定：(1)在调压室水位波动过程中，假定水库水位不发生变化；(2)不考虑水体的压缩性和引水管壁的弹性；(3)忽略调压室中的摩阻损失及惯性水头，因它与引水道中水头损失和惯性水头相比相当小[8]。气垫式调压室的基本方程如下：

气垫式调压室中水流的连续方程：

(1)

式中：Z为调压室水位；t为时间；F为调压室的截面积；Q为引水隧洞的流量；Qa为压力管道中的流量。

引水隧洞的动力方程：

(2)

式中：Zr为上游水库水位；Hp为气垫式调压室断面的测压管水头；K为水流进出气垫式调压室时的阻力系数，流入和流出应取不同的数值；Qs为进出调压室的流量；R为引水隧洞的沿程损失和局部损失系数；g为重力加速度；A为隧洞的截面积；L为隧洞的长度。

对气垫式调压室有压力平衡方程：

Hp=P+Z-Ha

(3)

式中：P为气垫式调压室气室绝对压力(以mH2O计)；Ha为当地大气压。

气垫式调压室气室内有气体状态方程PVn=常数，气垫式调压室的运行主要采用等PV值的控制方式[9]。气垫式调压室的截面积F不变，等PV值也就是等PL值。

则对气垫式调压室气体状态方程可以写为：

P(Z1-Z)n=C

(4)

式中：Z1为气垫式调压室折算顶高程；n为气体多方指数；C为气室常数。

当设计选用的气室常数C0值一旦确定后，对某一特定的水电站工程，应遵守P0L0=C0的控制准则。控制水库正常蓄水位电站不发电(全部停机)工况下气垫式调压室内的水深为h0，此时的气室高度为L0=h-h0(h为折算后的气垫式调压室总高度，L0为折算后的气室高度)，根据设有气垫式调压室的水电站引水系统能量方程和压力平衡关系式(5)得出此时气室内的绝对压力P0，以该工况作为气室常数P0L0=C0的设计取值工况。

P0=L0+Zr-Z1-RQ2+Ha

(5)

气垫式调压室的气体状态方程(4)对时间t求导数得：

(6)

压力管道中的流量Qa随时间变化，设导叶或喷针直线关闭或开启，当t=0时刻，有Qa=Aa0，则：

Qa=kt+Qa0

(7)

Q=Qa+Qs

(8)

式中：K为压力管道中的流量随时间变化时直线的斜率，反映了压力管道的流量变化规律；Qa0为初始时刻压力管道中的流量；其它符号意义同前。

将(7)式带入到(1)式得：

(9)

将式(9)带入到式(6)得：

(10)

将式(3)、(7)、(8)代入到式(2)得：

(11)

方程(9)、(10)、(11)中有三个随时间变化的变量，分别为气垫式调压室水位Z、气室绝对压力P和引水隧洞流量Q，可以采用多种数学手段求解。为了保证计算精度以及方便求解，可采用定步长的四阶龙格——库塔法[10]。进行调压室水位波动计算时，从初始时刻进行，即初始时刻的气垫式调压室水位Z0、气室内的绝对压力P0、引水隧洞流量Q0应为已知量。初始时刻各变量的求解方法可采用对应引水隧洞流量为Q0时的气室常数C0值与电站不发电时的气室常数C0值相同来求取，将电站不发电时的气室压力作为控制压力。

3 工程实例及状态方程多方指数的影响计算

某水电站引水隧洞长6 192.145 m，隧洞断面为城门洞形，过水断面底宽4.4 m，高5.1 m，水库正常蓄水位为2 147.0 m。压力管道采用一条主管，经一个卜形岔管分为两条支管分别向厂房内两台水斗式水轮发电机组联合供水的布置方式，水轮机引用流量为39 m3/s。气垫式调压室采用长廊型，城门洞形断面，宽10 m，高15 m，长140 m。气垫式调压室底板高程1 857.15 m，拱顶高程1 872.15 m。折算调压室总高度为13.93 m， 折算气垫式调压室顶高程1 871.08 m，如图2为气垫式调压室结构图。

图2 某气垫式调压室结构图

算例中水轮机喷针关闭时间为24 s，开启时间为28 s，按直线规律关闭或开启。气垫式调压室内的水位波动与引水隧洞糙率大小有关[11]，根据相关设计规范要求，气垫式调压室的最高涌浪水位在计算时引水隧洞拟取较小糙率值，最低涌浪水位在计算时引水隧洞拟取较大糙率值。

气垫式调压室中的气体体积(与水位对应)和压力变化应遵循理想气体状态方程，也就是遵循多方指数状态方程PLn等于常数的规律变化。等温过程n=1.0，绝热过程n=1.4，非等温和非绝热n介于1.0与1.4之间。通常认为，因水库水位发生变化而引起的气垫式调压室内气体状态发生变化或调压室气体泄漏而导致的气室压力变化，其变化过程缓慢，可近似认为是等温过程。对于电站甩负荷或增负荷引起的气垫式调压室内水位和气室压力变化，由于这些过程中气体的压缩或膨胀是在相对较短时间内完成的，调压室内气体与边界并没有进行充分的热交换，可近似认为是绝热过程。实际变化过程既非等温过程也非绝热过程，为说明状态方程多方指数n对气垫式调压室水位变化以及气室压力变化的影响，分别对甩负荷工况和增负荷工况计算多方指数分别取1.0、1.1、1.2、1.3、1.4进行计算比较。计算中气室常数C0值取2 914.852 m2。

甩负荷工况计算：上游水库取正常的蓄水位为2 147.0 m，电站2台→0甩负荷，计算结果如表1和图3、图4：

从甩负荷工况计算可知，对甩负荷工况，在状态方程多方指数取值为1.0时，气垫式调压室涌浪水位有最大值，调压室水位波动的幅度最大，不

图3 甩负荷工况不同多方指数调压室水位变化情况

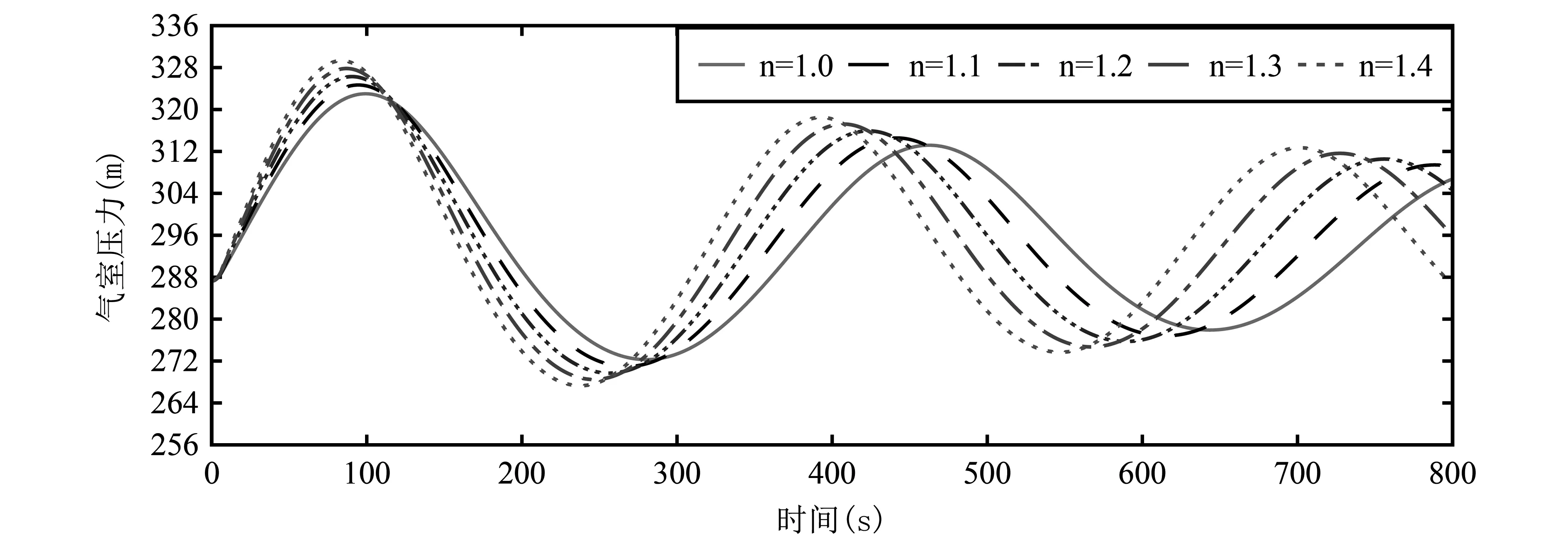
图4 甩负荷工况不同多方指数气室压力变化情况

表1 甩负荷工况不同多方指数计算结果

同n值时丢负荷后最低涌浪水位相差不大。在状态方程多方指数取值为1.4时，气垫式调压室的气室压力有最大值和最小值，气室压力变化的范围最大。随着多方指数n的增大，气垫式调压室水位波动的最高涌浪水位减小，气室压力的最大值增大。

增负荷工况计算：上游水库取正常蓄水位为2 147.0 m，电站1台→2台增负荷，计算结果如表2和图5、图6。

从增负荷工况计算可知，在状态方程多方指数取值为1.0时，气垫式调压室涌浪水位有最小值。在状态方程多方指数取值为1.4时，气垫式调压室的气室压力有最小值。

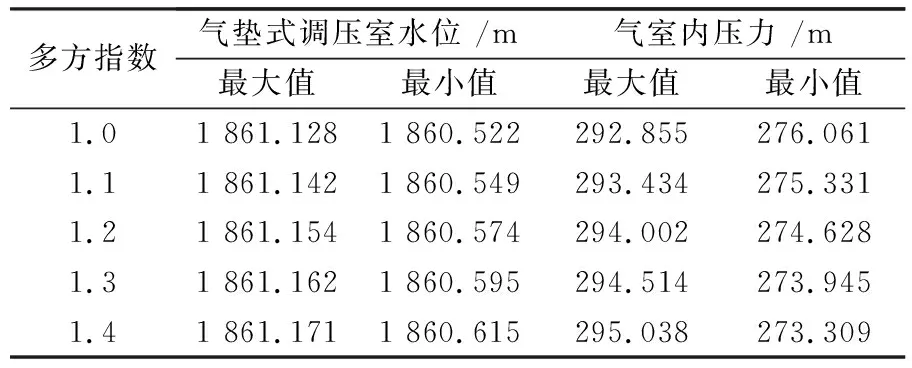
表2 增负荷工况不同多方指数计算结果

对于算例工程，电站两台机组甩负荷后的气垫式调压室最低涌浪水位低于电站1台→2台增负荷时的最低涌浪水位。因此该工程气垫式调压室最高涌浪水位可取1 862.052 m，最低涌浪水位可取1 860.377 m。气室最大压力(绝对压力)可取329.018 m，最小压力可取267.451 m。根据上述计算分析，若以控制气垫式调压室最高、最低水位为目的，拟取多方指数1.0计算，若以控制气垫式调压室气室最高、最低压力为目的，拟取多方指数1.4计算。

4 结 语

气垫式调压室水位和气室压力波动是规划和

图5 增负荷工况不同多方指数调压室水位变化情况

图6 增负荷工况不同多方指数气室压力变化情况

设计气垫式调压室所关心的问题。本文针对这些问题，从理论上推导了气垫式调压室水位和压力波动所满足的微分方程组气垫式调压室水位波动计算所满足的微分方程组，采用四阶龙格——库塔法可快速求解气垫式调压室水位波动过程以及气室压力变化过程，计算所需要的资料较少，数据整理工作简单，对中小型水电站，可优先采用四阶龙格——库塔法进行气垫式调压室的体型设计。同时，从气体状态方程多方指数对调压室涌浪水位和气室压力的影响进行分析，指出在水力过渡过程计算中以控制气垫式调压室最高、最低水位为目的，气体状态方程多方指数宜取1.0；若以控制气垫式调压室气室最高、最低压力为目的，多方指数宜取1.4。